はじめに
感覚的に、管理図はちょっと重い、でも回帰でみると荒い、その中間あたりでと興味を持ったのがProphet。
なぜProphetかというと、全体傾向をトレンドと季節成分と誤差に分解できるから。
誤差を超えたら「異常が生じたかもしれない」、トレンドに変化があれば「変化(及び効果)があったかもしれないと気がつきやすいのではないかと。
月次返品データで主に見ているのは、当月返品に異常はないか?ということ。
もうひとつは、すでに異常となったものを処置した場合や変更を行ったその後の効果だ。
また、来月の返品がどうなるかということを予測したい訳ではないが、今後返品がどのように推移するのかは掴めるといい。
ある製品の月次返品データが手元にある。
このデータにおける月次返品数は、変動が非常に大きい状態にあったが、ある時期に行った変更により返品数は減少しているというもの。
予測は、実変動に対しある程度は沿ってほしいし、減少などトレンドが変わったことも認識したい。
以上のことから、以下を実施してみた。
1.(まずは)従来通り、実績データで単純プロットと回帰直線を描く。
2.変更前の実績データで学習した時の先の予測と実績の差を見る。
3.直近3か月前までの実績データで学習した時の直近3か月のあてはまりを見る。
実行条件など
- Google colabで実行
- 手元にある月次返品データ(当記事の末尾にデータ有)で実行
| ds | y |
|---|---|
| Dateです | 返品数です |
このライブラリの使い方について
- 月次の時系列データ(例:「年月」と「出荷数」等)で先の予測や異常検知を行うためのライブラリ。
- 直近から何か月前までをテストデータにするか、直近より先 何か月を予測するかを任意に設定可能。(直近3か月前までをテストデータとした場合、テストデータ以前のデータが学習データになる)
- マクロトレンドと季節性が分解されるので、単純な直線回帰よりもあてはまりのよい判断につながることが期待できる。
- 先の予測だけではなく、異常検出(=上下限を超える時)としても活用することができる。
前準備
- csvデータは以下の形式(例:年月と返品)とする。
- 1列目を『年月』、2列目を『目的変数』とする。 ※データは1,2列のみ。
- [注意] csvデータは文字コードを「UTF-8」とする。
| 年月 | 返品 | →自動変換→ | ds | y |
|---|---|---|---|---|
| 2019/1 | 4 | →自動変換→ | 2019-1-1 | 4 |
| 2019/2 | 12 | →自動変換→ | 2019-2-1 | 12 |
| 2019/3 | 6 | →自動変換→ | 2019-3-1 | 6 |
| … | … | →自動変換→ | … | … |
| 2021/12 | 1 | →自動変換→ | 2021-12-1 | 1 |
実行手順
- メニューバーの「ランタイム」から「すべてのセルを実行」をクリック。
- ライブラリインストール完了後、[ファイル選択]ボタンをクリックし、分析したい文書(csvファイル)を指定する。
- 「季節変動のモデル」を選択する。(加法モデル:additive、乗法モデル:multiplicative):通常は加法モデルでよいが、あてはまりから適切な方を選ぶ
- テスト期間(最新 -nヵ月)、予測期間(最新 +nヵ月)を設定する。
- [注意] 一度実行した後にモデルや期間を変更する場合は、すべてのセルを再実行。
ライブラリインストール&インポート
#日本語フォントをインストール
!apt-get -y install fonts-ipafont-gothic
#Prophetのインストール
pip install prophet
#matplotlib日本語化
pip install japanize-matplotlib
#ライブラリインポート
import os
import pandas as pd
import sklearn
import csv
import datetime
import numpy as np
import japanize_matplotlib
import seaborn as sns
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
import seaborn as sns
import statsmodels.formula.api as sm
%matplotlib inline
```Python:
#Prophetインポート
from fbprophet import Prophet
import fbprophet.plot as fp
#Plotlyインポート
import plotly.express as px
import plotly.io as pio
pio.renderers.default = "colab"
データ読込み/モデル条件設定
#@title csvファイル(UTF-8)を指定してください
from google.colab import files
#print('csvファイル(UTF-8)を指定してください')
uploaded = files.upload()
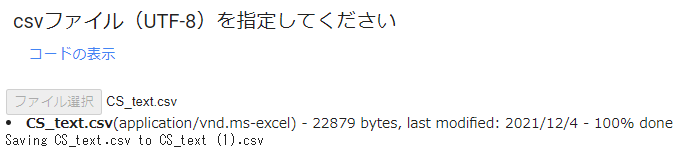
※ライブラリのインストールとインポートが完了すると、[ ファイル選択 ]がうながされるので、クリックし、ファイルを指定。(キャプチャ画像はファイル読込み後の画面イメージ)
#@title 季節変動のモデル選択(加法モデル:additive、乗法モデル:multiplicative) { run: "auto" }
Seasonality_Model = 'multiplicative' #@param ['multiplicative'] {allow-input: true}
#@title テスト期間(最新 -nヵ月) { run: "auto" }
Latest_months_ago = -40 #@param{type:"number"}
#@title 予測期間(最新 +nヵ月) { run: "auto" }
Predict_future_months = 3 #@param{type:"number"}
##データ前処理
#@title データフレーム格納
if len(uploaded.keys()) != 1:
print("アップロードは1ファイルにのみ限ります")
else:
target = list(uploaded.keys())[0]
df = pd.read_csv(target)
df.columns = ['ds','y']
df
#dsをdatetime形式に
df["ds"] = pd.to_datetime(df["ds"])
df["ds"]
実績データ(折れ線グラフと単回帰)
#@title 時系列データ
df.plot(x="ds", y="y")
plt.plot()
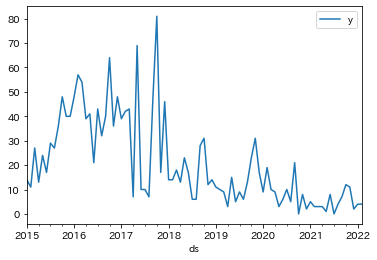
返品は、2015年から2016年にかけて増加。
その後、かなり変動は大きいものの返品傾向を維持、2019年以降、返品は減少に転じている。
#@title 回帰直線(datetime→数値変換)
df['ds_numeric']=df['ds'].map(datetime.datetime.toordinal)
x=df['ds_numeric']
y=df['y']
sns.regplot(x, y)
plt.plot()
from sklearn.linear_model import LinearRegression
clf = LinearRegression()
clf.fit(df[["ds_numeric"]], df["y"])
#print("回帰係数=", clf.coef_)
#print("切片:",clf.intercept_)
print(" 単回帰式 y = %.2fx + %.2f" %(clf.coef_,clf.intercept_))
print(" 決定係数 R^2 =",clf.score(df[["ds_numeric"]], df["y"]))
corr = np.corrcoef(x,y)
print(" 相関係数 r =",corr[0,1])
単回帰式 y = -0.01x + 10852.56
決定係数 R^2 = 0.38783109079407085
相関係数 r = -0.6227608616427881
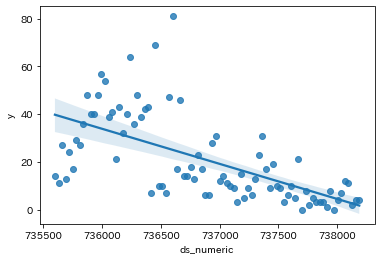
相関係数は-0.62。強いとはいえないがマイナスの相関あり。
データばらつきが大きいため、回帰だけで予測するのはむつかしい。
Prophet適用
#@title 学習データ/テストデータの設定
df_train = df[:Latest_months_ago]
df_test = df[Latest_months_ago:]
#以下のような指定もできる
#df_train = df[df["DATE"] <= "2019-7-1"]
#df_test = df[(df["DATE"] >= "2019-8-1")]
train_size = len(df_train)
test_size = len(df_test)
train_size, test_size
#@title Prophet適用
m = Prophet(weekly_seasonality=False,daily_seasonality=False,
seasonality_mode = Seasonality_Model
)
m.fit(df_train)
#@title 予測期間の設定と予測(期間は periods = n にて設定、freq="M"ならば月、freq="D"ならば日)
future = m.make_future_dataframe(periods=(Latest_months_ago*-1+Predict_future_months), freq="M")
forecast = m.predict(future)
forecast
Prophet予測結果(グラフ表示)
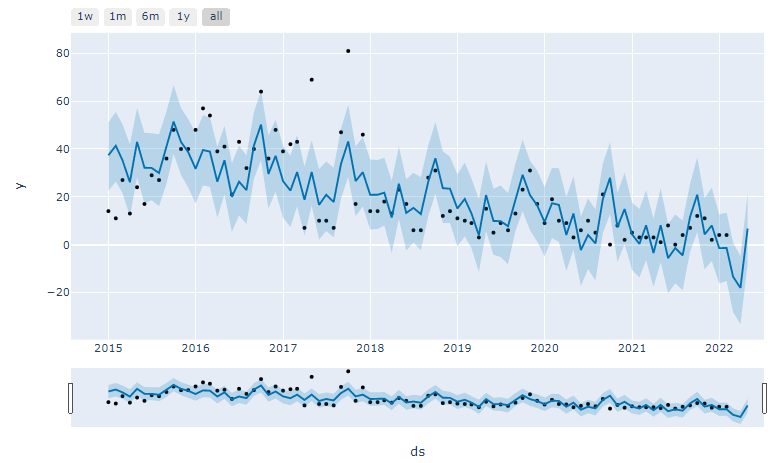
#@title 実績と予測のあてはまり(打点が実績、折れ線と幅が予測)
m.plot(forecast)
plt.plot(df[train_size: train_size+test_size].ds, df[train_size:train_size+test_size].y, ".", color="red", alpha=0.6)
plt.plot()
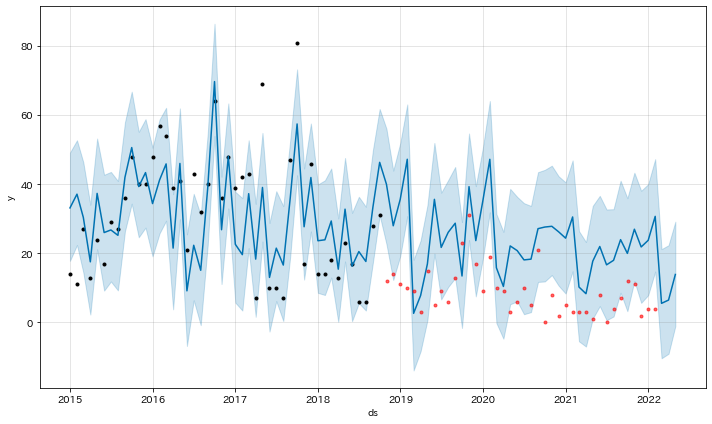
製品に変更を加えた前後の違いをみたかったので、2018年10月までの実績で学習し、その先を予測したもの。
打点(黒)が学習に利用した実績データ、打点以降の折れ線が予測データ。打点(赤)が予測のあてはまりを見るテストデータ(これも実績データ)。
テストデータは、予測を大きく下回っている。多くの打点が信頼区間(下限)を下回っており、予測が外れたというのではなく、変更実施により傾向が異なったことが見て取れる。
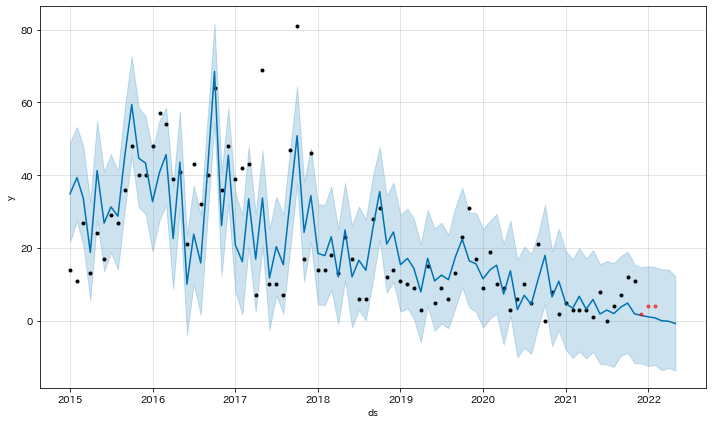
これは、直近3か月前までのデータをテストデータ、それ以前を学習データとした場合のグラフ。
予測幅はやや広いが、予測とテストデータのあてはまりは悪くない。
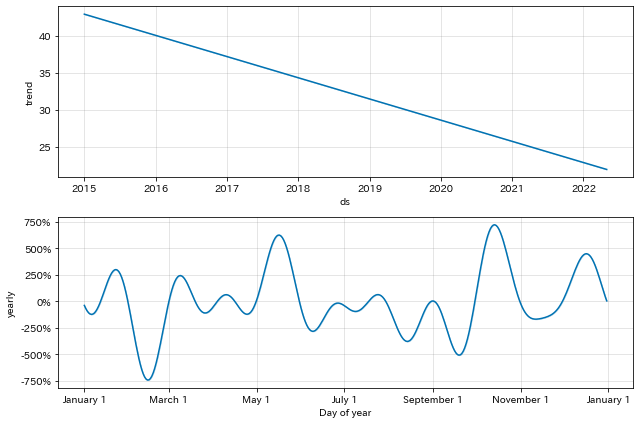
#@title トレンドと季節性でグラフ化
fig1 = m.plot_components(forecast)
上のグラフが 季節性のない成長度合い 、下のグラフが 季節性を表現 したグラフ。上のグラフは回帰のイメージ。直線的な増・減・維持傾向となり、下は文字通り、季節変動となる。
Plotlyによる動的グラフ化(インタラクティブに拡大・縮小・範囲指定)
#@title 動的グラフ表示(全データ使用)
model = Prophet()
model.fit(df)
future_all = model.make_future_dataframe(periods=3, freq="M")
forecast_all = model.predict(future_all)
fig_plotly = fp.plot_plotly(model, forecast_all)
fig_plotly.show()
最後に
月次データなので、変動にどこまでついてくるか・・・と半信半疑であったが、ソコソコついてくる。
過度な予測精度には拘らず、当月の返品が「信頼区間からはみ出す=異常かもしれない」という気付きや、変更や改善を行った場合の効果確認等において活用できそう。
参考サイト
使用したデータ
ds y
2015/1/1 0:00 14
2015/2/1 0:00 11
2015/3/1 0:00 27
2015/4/1 0:00 13
2015/5/1 0:00 24
2015/6/1 0:00 17
2015/7/1 0:00 29
2015/8/1 0:00 27
2015/9/1 0:00 36
2015/10/1 0:00 48
2015/11/1 0:00 40
2015/12/1 0:00 40
2016/1/1 0:00 48
2016/2/1 0:00 57
2016/3/1 0:00 54
2016/4/1 0:00 39
2016/5/1 0:00 41
2016/6/1 0:00 21
2016/7/1 0:00 43
2016/8/1 0:00 32
2016/9/1 0:00 40
2016/10/1 0:00 64
2016/11/1 0:00 36
2016/12/1 0:00 48
2017/1/1 0:00 39
2017/2/1 0:00 42
2017/3/1 0:00 43
2017/4/1 0:00 7
2017/5/1 0:00 69
2017/6/1 0:00 10
2017/7/1 0:00 10
2017/8/1 0:00 7
2017/9/1 0:00 47
2017/10/1 0:00 81
2017/11/1 0:00 17
2017/12/1 0:00 46
2018/1/1 0:00 14
2018/2/1 0:00 14
2018/3/1 0:00 18
2018/4/1 0:00 13
2018/5/1 0:00 23
2018/6/1 0:00 17
2018/7/1 0:00 6
2018/8/1 0:00 6
2018/9/1 0:00 28
2018/10/1 0:00 31
2018/11/1 0:00 12
2018/12/1 0:00 14
2019/1/1 0:00 11
2019/2/1 0:00 10
2019/3/1 0:00 9
2019/4/1 0:00 3
2019/5/1 0:00 15
2019/6/1 0:00 5
2019/7/1 0:00 9
2019/8/1 0:00 6
2019/9/1 0:00 13
2019/10/1 0:00 23
2019/11/1 0:00 31
2019/12/1 0:00 17
2020/1/1 0:00 9
2020/2/1 0:00 19
2020/3/1 0:00 10
2020/4/1 0:00 9
2020/5/1 0:00 3
2020/6/1 0:00 6
2020/7/1 0:00 10
2020/8/1 0:00 5
2020/9/1 0:00 21
2020/10/1 0:00 0
2020/11/1 0:00 8
2020/12/1 0:00 2
2021/1/1 0:00 5
2021/2/1 0:00 3
2021/3/1 0:00 3
2021/4/1 0:00 3
2021/5/1 0:00 1
2021/6/1 0:00 8
2021/7/1 0:00 0
2021/8/1 0:00 4
2021/9/1 0:00 7
2021/10/1 0:00 12
2021/11/1 0:00 11
2021/12/1 0:00 2
2022/1/1 0:00 4
2022/2/1 0:00 4