##~連続量もしくは 0/1データ の結果を予測する~
- 2020/9/2:決定木の分析過程の説明、手元データでの「決定木(回帰)」解析結果を追加
##はじめに
Pythonでデータ分析・・・私にとってはマダマダ夢物語に近いが、こんな私でも「見よう見まねでできるようにはなるかも?!」という気にさせてくれるのが、『データサイエンス塾!!』さんの動画だ。
多くの動画をアップしておられるが、再生リストのなかに「とてもよくわかる機械学習の基本」というタイトルの再生リストがあり、
このなかで「重回帰分析」「ロジスティック回帰分析」と「決定木」が取り上げられた動画#4~#6について、私が倣って実施してみた備忘を記録するもの。
###実行条件など
・Google colabで実行
###概要説明
『先を予測したい!』
こんな時に、もっとも利用されてるのは「単回帰分析」だと思いますが、ご存じの通り、これは y = ax+b というシンプルなモデルなので、例えば目的変数y が[売上]の時、[売上]をあるひとつの説明変数x で表現するのは至難。
なので、より多くの説明変数x を取り上げることができる「重回帰分析」の方がいいよということになるが、実行するのは簡単ではない。
また、目的変数y が[0/1]データ(例えば[成功/失敗]、[検出/非検出]、[すき/きらい]のような2値)のときは「ロジスティック回帰」で分析しないといけないが、”対数変換しないといけないんんよね?”、ムムム・・・さらにハードルがあがるではないかぁ。
まぁ、とにかく、こんな感じの方も多いのではないかと思う。
「データサイエンス塾!!」さんが、こんな我々のような者を察して動画を作成されているのかどうかまではわかりませんが、『「重回帰」も「ロジスティック回帰」もPython使えばこんなに簡単にできますよ』というのを、とても身近な事例データで示してくださっています。
そして最後のトドメは「決定木」。
私は名前を聞いたことがあるという程度・・・でしたが、説明を聞き「分類も予測もできるのか!」と驚いただけではなく、出力される図の完成度の高さに圧倒されました。まるでプロ依頼した調査の結果のようです。
事例データが「回帰分析」で使用されたデータと同じデータというのも、理解の助けになりました。
「とてもよくわかる機械学習の基本(動画#4~#6)」の例題について
- 「重回帰分析」 では「アイスクリームの売上」のデータが例題として扱われています。
説明変数Xは "temperature", "price", "rainy(0/1)"、目的変数yは "sales"となっていて、 "temperature", "price", "rainy"によって"sales"がどうなるかを予測するというものとなっています。
- 「ロジスティック回帰分析」 では「あるアプリへの登録/未登録」のデータが例題として扱われています。
説明変数は ”sex(0/1)”,”student(0/1)”,”stay home”、目的変数yは ”registration(0/1)” となっています。
”sex”,”student”,”stay home”によって"registration"がどうなるかを予測するというものになっています。
- 「決定木」では、分類と回帰の2パターンの分析がなされており、分類では「ロジスティック回帰分析」の例題データ、回帰では「重回帰分析」の例題データが用いられています。
ライブラリのインストールとインポート
Google colabでグラフを描画すると、(私の環境では)日本語が文字化けするので、まず以下をインストールしています。
※文字化けしない方は無視してもいいです。
pip install japanize-matplotlib
次にライブラリのインポートです。私はどのライブラリが必要かを逐次判断するのは面倒なので、基本、以下をデフォルトでインポートしています。(雑ですいません)
# Import required libraries
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
sns.set(font="IPAexGothic")
from scipy.stats import norm
pip install statsmodels
pip install dtreeviz
###データの読み込み
例題ファイル(CSV)をダウンロードし、Google colabにアップロードします。
ダウンロード対象ファイルは以下4つです。
※Google Colabへのアップロードの方法はここでは述べません。
##重回帰分析
まずは「重回帰分析」です。
読込むデータは2つあり、以後、これで「アイスクリームの売上」の予測を行うという流れになります。
以下のコードを実行すると、アイスクリームの売上実績データである「sales.csv」が「df_past」というデータフレームに、アイスクリームの売上を予測したいデータ「sales_future.csv」が「df_future」に格納されます。
df_past = pd.read_csv('4-4_sales.csv')
df_future = pd.read_csv('4-4_sales_future.csv')
「df_past」のカラムを見てみましょう。
df_past.columns
- Index(['temperature', 'price', 'rainy', 'sales'], dtype='object')
この例では、"temperature", "price", "rainy" という説明変数Xで、"sales"という目的変数yを予測することになりますので、まず、以下のコードでX,yの割り当てを行います。
X_name = ['temperature', 'price', 'rainy']
X = df_past[X_name]
y = df_past['sales']
X,y が割当てられれば、早速、重回帰分析の実行です。
なお、[sm.OLS]の [OLS] は線形回帰で、m.add_constant(X)は切片付きで求める指示となるようです。
import statsmodels.api as sm
model = sm.OLS(y,sm.add_constant(X))
result = model.fit()
result.summary()

これが、重回帰分析の結果です。
priceのP値(出力された表の P>|t| の値)が≧0.05となっていますので、説明変数から取り除くことを検討してもよさそうです。Adj.R-squared(自由度調整済決定係数)は0.825であり悪くはありません。
この結果を受け、説明変数からPriceを除いて、再度、Xを割り当てます。
X_name = ['temperature', 'rainy']
X = df_past[X_name]
y = df_past['sales']
もう一度、重回帰分析を実行します。
import statsmodels.api as sm
model = sm.OLS(y,sm.add_constant(X))
result = model.fit()
result.summary()

これが、説明変数からpriceを取り除いて再実行した重回帰分析の結果です。
説明変数のP値(出力された表の P>|t| の値)はいずれも≦0.05となっています。Adj.R-squared(自由度調整済決定係数)は0.826であり、これは先ほどの結果と違いはほとんどありません。
###予測
最後に、予測です。
あらかじめ用意されていた「df_future」のデータの予測値を算出します。
result.predict(sm.add_constant(df_future[X_name]))
以下が出力値です。
0 692.242462
1 804.817001
2 399.804427
3 811.363808
4 890.584370
dtype: float64
関係式は以下になりますので、予測データのひとつ目のデータのみ確認してみます。
- y(sales) = tempereture × coef + rainy × coef + const(切片)
- y(sales) = 12.6℃ × 47.6485 + 1 × 178.0815 + (-86.2107) = 692.2419
##ロジスティック回帰分析
次は「ロジスティック回帰分析」です。
読込むデータは2つあり、以後、これで「あるアプリへの登録/未登録」を予測するという流れになります。
以下のコードを実行すると、あるアプリへの登録/未登録の実績データ「user_data.csv」が「df_past」というデータフレームに、アイスクリームの売上を予測したいデータ「user_data_future.csv」が「df_future」に格納されます。
df_past = pd.read_csv('4-5_user_data.csv')
df_future = pd.read_csv('4-5_user_data_future.csv')
「df_past」のカラムを見てみましょう。
df_past.columns
- Index(['sex', 'student', 'stay time', 'registration'], dtype='object')
この例では、'sex', 'student', 'stay time' という説明変数X で、'registration'という目的変数y を予測することになるので、まず、以下のコードで X,y の割り当てを行います。
X_name = ['sex', 'student', 'stay time']
X = df_past[X_name]
y = df_past['registration']
X,y が割当てられれば、早速、ロジスティック回帰分析の実行です。
なお、インポートライブラリや、重回帰で [sm.OLS] とされていた箇所が [sm.Logit] とされる点が重回帰との違いとなってます。
import statsmodels.api as sm
from sklearn.linear_model import LogisticRegression #ロジット回帰の場合、このライブラリが必要
model = sm.Logit(y,sm.add_constant(X))
result = model.fit()
result.summary()

これが、ロジスティック回帰分析の結果です。
sexのP値(出力された表の P>|z| の値)か≧0.05となっていますので、説明変数から取り除くことを検討してもよさそうです。
この結果を受け、説明変数からsexを除き、再度、X を割り当てます。
X_name = ['student', 'stay time']
X = df_past[X_name]
y = df_past['registration']
もう一度、ロジスティック回帰分析を実行します。
import statsmodels.api as sm
from sklearn.linear_model import LogisticRegression #ロジット回帰の場合、このライブラリが必要
model = sm.Logit(y,sm.add_constant(X))
result = model.fit()
result.summary()

説明変数からsexを取り除いて再実行したロジスティック回帰分析の結果です。
説明変数のP値(出力された表の P>|z| の値)はいずれも≦0.05となっています。
目的変数は、よりすくない説明変数で説明できたほうがよいですが、Pseudo R-squ.が説明変数を取り除く前後で大きく変わらないことは確認しておいた方がよいようです。
この例では、先ほどとの違いはほとんどありません。
###予測
最後に、あらかじめ用意されていた「df_future」のデータの予測値を算出します。
result.predict(sm.add_constant(df_future[X_name]))
以下が出力値です。
0 0.617041
1 0.292847
2 0.034132
3 0.815431
4 0.508296
5 0.082051
6 0.461241
7 0.715211
8 0.382695
9 0.607463
dtype: float64
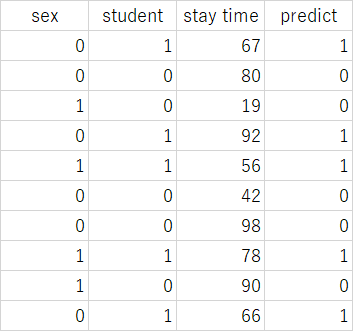
予測データと予測値(predict)の対応は以下の通りとなりました。
この事例の目的変数yは、registration=1,not registration=0 なので、予測値(predict)は、0~1の確率として表現されています。

##決定木分析(分類編)
CSVファイルの読み込み
以下コードの実行により、「df.past」というデータフレームに「user_data,csv」のデータが、「df_future」というデータフレームに「user_data_future」のデータが納められます。
#分類問題
df_past = pd.read_csv("4-5_user_data.csv")
df_future = pd.read_csv("4-5_user_data_future.csv")
X_name = ["sex","student","stay time"]
y_name = "registration"
X = df_past[X_name]
y = df_past[y_name]
###決定木の実行
まず、「df‗past」に格納したデータを見てみます。
df_past.head()
次に「決定木」の実行に必要なライブラリをインポートします。
from sklearn import tree
from dtreeviz.trees import *
import graphviz
いよいよ、決定木分析の実行です。
dtree = tree.DecisionTreeClassifier(max_depth=2)
dtree.fit(X,y)
viz = dtreeviz(dtree,X,y,
target_name = y_name,
feature_names = X_name,
class_names = ["not register","register"])
viz
結果の考察

まず一つ目の分岐ですが、stay time が44.5以下か、44.5よりも大きいかで分かれています。
「stay time≦44.5」の時、「register」は[0]となっています。
次の分岐は student(学生)か否かです。「stay time>44.5」の場合に register はあらわれ、内訳としては student の方がregister されるケースが多いことがわかります。
とても分かりやすく、かつ見やすいですね。
ある条件の予測
次にある結果の予想です。
事例の説明変数Xは、sex, student, stay time の3つ。男性, 学生, 滞在時間50 の場合、これを数値で表すと、X = [1,1,50] になります。
これを引数にセットして予想してみます。
dtree = tree.DecisionTreeClassifier(max_depth=2)
dtree.fit(X,y)
viz = dtreeviz(dtree,X,y,
target_name = y_name,
feature_names = X_name,
class_names = ["not register","register"],
X = [1,1,50]
)
viz

男性,学生,滞在時間50 = [1,1,50]で予測した結果が表示されました。
予測条件は、各分岐のグラフ上で▲で示され、どちらの分岐かはオレンジの枠で囲われて示され、とてもよくわかります。
この例では、最終の予測結果が register となっています。
まとまった対象の予測
次に、予測したい対象一覧(df_futureに格納したもの)を取り込んで、予測にかけます。
dtree.predict(df_future)
- array([1, 0, 0, 1, 1, 0, 0, 1, 0, 1])
分類予測データと分類予測結果(predict)の対応は以下の通りとなりました。
分類予測データでstudent=1となっているデータは、stay time≧44.5 となっていますので、student=1 → predct=1 となっています。先ほどの図表記の内容からもこの結果は素直に読み取れます。
##決定木分析(回帰編)
まず、この分析で使用するデータを読込みます。
#回帰問題
df_past = pd.read_csv("4-6_sales.csv")
df_future = pd.read_csv("4-6_sales_future.csv")
X_name = ["temperature", "price", "rainy"]
y_name = "sales"
X = df_past[X_name]
y = df_past[y_name]
早速、分析を行います。
dtree = tree.DecisionTreeRegressor(max_depth=2)
dtree.fit(X,y)
viz = dtreeviz(dtree,X,y,
target_name = y_name,
feature_names = X_name,
#X = [20,220,0]
)
viz

はじめにtemperature(19.35℃以下 or 19.35℃より大きい)で分岐し、次もtemperatureで分岐しています。
左側の分岐から先は、14.2℃以下なら sales は400.93に, 14.2℃より大きいなら609.00に、
右側の分岐から先をみると、24.9℃以下ならsalesは873.44に, 24.9℃より大きいならsalesは1347.33となっています。
temperatureがsalesに影響していること、それぞれの分岐においてどの程度のsalesとなるかがわかります。
ある条件の予測
次にある条件の予測です。
事例の説明変数Xは、temperature, price, rainy の3つ。20℃, 220円, 晴れ の場合、これを数値で表すと、X = [20,220,0] になります。
これを引数にセットして予測します。
dtree = tree.DecisionTreeRegressor(max_depth=2)
dtree.fit(X,y)
viz = dtreeviz(dtree,X,y,
target_name = y_name,
feature_names = X_name,
X = [20,220,0]
)
viz

20℃, 220円, 晴れ = [20,220,0]で予測した結果が表示されました。
予測条件は、各分岐のグラフ上で▲で示され、どちらの分岐かはオレンジの枠で囲われて示され、とてもよくわかります。
この条件におけるsales予測結果は[873.44]となっています。
まとまった対象の予測
次に、予測したい対象一覧(df_futureに格納したもの)を取り込んで、予測にかけます。
dtree.predict(df_future)
- array([470.93333333, 609. , 470.93333333, 609. , 873.44444444])
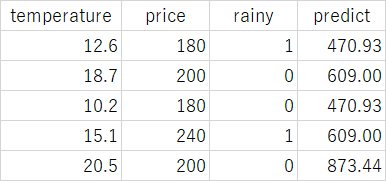
予測データと予測結果(predict)の対応は以下の通りとなりました。
先ほどの図表記の内容からもこの結果は素直に読み取れます。
手元にあったCSアンケート結果で「決定木(回帰)」を行ってみた
※2021/9/2追加
- データ数 = 169
- 説明変数は Tec.Skill(技術的フォロー)、Complain Act.(クレーム対応)、Call Act.(電話対応)、 Visit number(訪問回数)、Advice(アドバイス)、return act.(返品対応)、QA(保証期間)の7つ
- 目的変数は、S-CS(営業CS)。
- すべての項目が1~6の整数値。
- max_depth=2,3,4 とみた上、いちばん解釈しやすいと思えた [2] とした。
**重回帰分析**も行った
Complain Act.(クレーム対応)、Visit number(訪問回数)、QA(保証期間)は有意とならなかった。この説明変数を除いて行ったところ、すべてが高度に有意となり、自由度調整済決定係数はわずかによくなった。(0.842)
###考察
- アドバイス(Advice)のよしあしが最初の分岐となっている。
- アドバイス(Advice)が>4.5点(6.0点中)ならば、営業CSはほぼ5点(6.0点中)以上となっている。この上で電話対応(Call Act.)が抜群だと営業CSは満点に近づく。
- アドバイス(Advice)が≦4.5点(6.0点中)の場合でも、返品対応(return act.)が通常程度ならば営業CSは4点(6.0点中)、逆に返品対応(return act.)が2.5点を下回ると営業CSは1.25点(6.0点中)と極端に低下する。
⇒ 返品対応(return act.)に気を配り、確実に履行してゆきつつ、アドバイス(Advice)力を上げてゆくことができれば営業CSは高水準が維持できるのではないかと考えられる。
これまで、平均値を算出したり、ポートフォリオを描いたり、いろんな見方をしてきたが、この「決定木」による分析ほど状況を立体的に掴むことはできていなかったように思います。
「決定木」は、すごいな。
###参考サイト