【Unity】平面の鏡面反射を読み解く

Last updated at 2024-12-31Posted at 2024-12-30

はじめに

平面上で鏡面反射を実現するには、反射する平面と対となる反射用のカメラで構成するPlanar Reflectionと呼ばれる手法が用いられます。鏡面反射は床の情報量を簡単に増やせる一方、反射カメラによる描画負荷が生じるため仕組みをしっかり理解した上で使っていきたいところです。ここでは、自身の備忘録を兼ねつつ鏡面反射の手法を1つずつで読み解いていきます。

鏡面反射参考サイト

Unityで鏡面反射させる方法はネットで調べるとたくさんあります。

どのサイトも基本的には同じ手法を用いて鏡面反射を実現しています。今回は一番シンプルでわかりやすい最初に挙げた以下のサイトを参考に解説していきます。感謝

仕組み

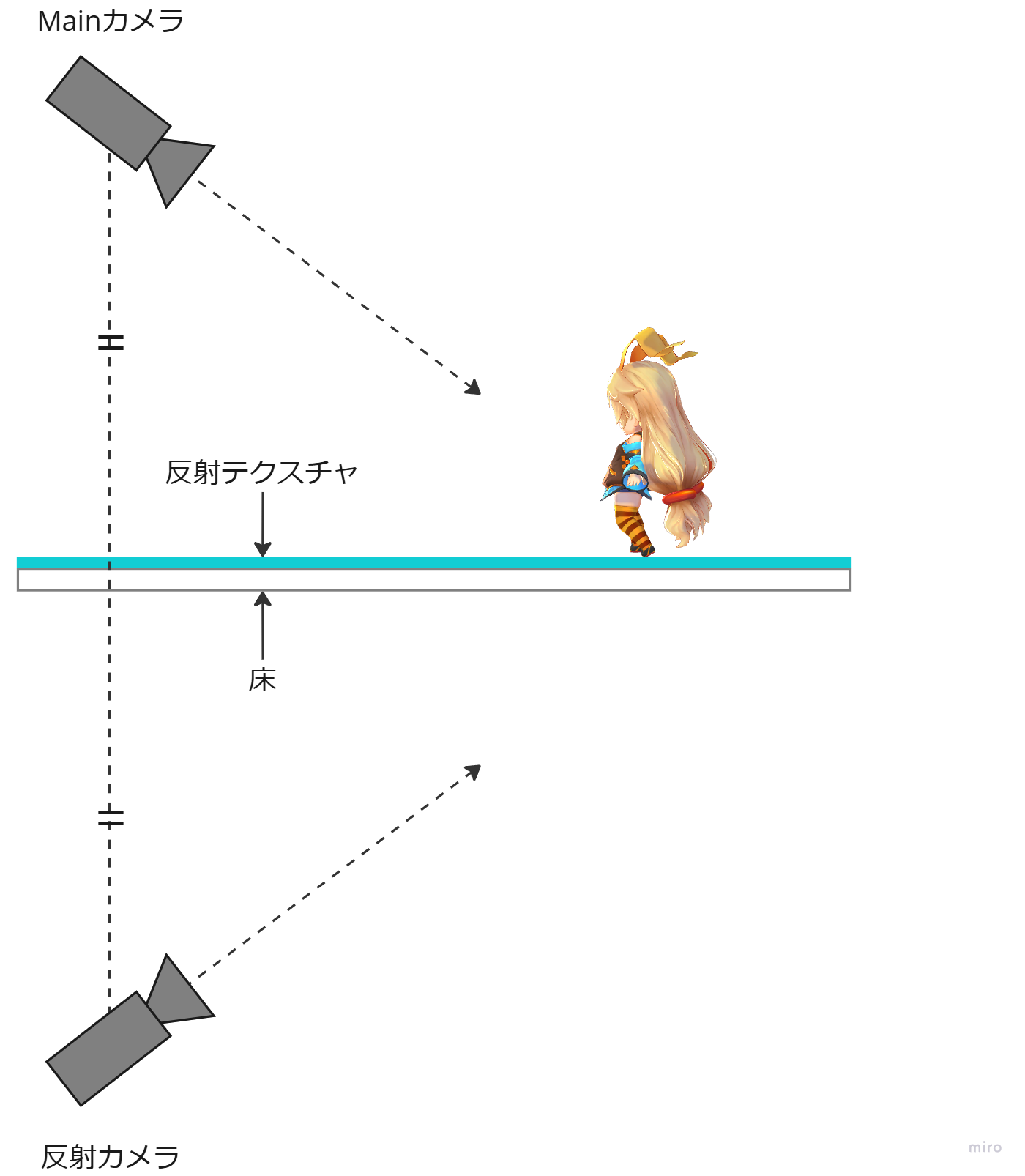
Planar Reflectionの仕組みは以下の図のようになっています。鏡面反射をさせるには、床面を基準にMainカメラと対となる反射カメラを用意します。この反射カメラの描画を床のテクスチャに反映させることで実現しています。

反射カメラの描画

Mainカメラの描画(鏡面反射をさせない場合)

反射カメラの描画を床面に適用+Mainカメラ描画

この例ではGameViewに描画するMainカメラと対となる反射カメラで描画を行っているため、SceneViewでは正しく表示されません。SceneViewでも適切に反射描画させるためには、SceneViewカメラの位置から反射カメラの位置計算を同様に行う必要があります。

SceneViewへの描画は負荷も増加するのと、今回は必要最低限の機能解説に留めるため省略しています。

コードと設定

全体のC#スクリプトとシェーダーは以下の通りです。

MirrorReflection.cs

using UnityEngine;

public class MirrorReflection : MonoBehaviour {

    private Camera m_MainCamera;
    private Camera m_RefCamera;
    private Material m_MatRefPlane;
    private RenderTexture m_RefTexture;
    
    private readonly int m_RefTexId = Shader.PropertyToID("_ReflectionTex");

    private void Start() {
        m_RefTexture = new RenderTexture(Screen.width, Screen.height, 24, RenderTextureFormat.ARGB32);

        m_MainCamera = Camera.main;

        m_RefCamera = gameObject.AddComponent<Camera>();
        m_RefCamera.cullingMask &= ~(1 << LayerMask.NameToLayer("Mirror"));
        m_RefCamera.enabled = false;
        m_RefCamera.hideFlags = HideFlags.HideAndDontSave;

        m_RefCamera.targetTexture = m_RefTexture;
        m_MatRefPlane = transform.GetComponent<Renderer>().sharedMaterial;
        m_MatRefPlane.SetTexture(m_RefTexId, m_RefTexture);
    }

    private void OnDestroy() {
        if (m_RefTexture == null) return;
        Destroy(m_RefTexture);
        m_RefTexture = null;
    }

    private void SetReflectionCamera() {
        // 平面の方程式を作成
        Vector3 planeNormal = transform.up;
        Vector3 planePos = transform.position;
        float d = -Vector3.Dot(planeNormal, planePos);
        Vector4 plane = new Vector4(planeNormal.x, planeNormal.y, planeNormal.z, d);
        
        // 反射行列の生成
        Matrix4x4 refMatrix = CalcReflectionMatrix(plane);
        // ワールド空間の反射行列を反射カメラのビュー行列で変換して代入
        m_RefCamera.worldToCameraMatrix = m_MainCamera.worldToCameraMatrix * refMatrix;

        // 床の下を貫通するオブジェクトを表示させないように
        Vector3 cPos = m_RefCamera.worldToCameraMatrix.MultiplyPoint(planePos);
        Vector3 cNormal = m_RefCamera.worldToCameraMatrix.MultiplyVector(planeNormal).normalized;
        Vector4 clipPlane = new Vector4(cNormal.x, cNormal.y, cNormal.z, -Vector3.Dot(cPos, cNormal));

        m_RefCamera.projectionMatrix = m_MainCamera.CalculateObliqueMatrix(clipPlane);
    }

    private Matrix4x4 CalcReflectionMatrix(Vector4 n) {
        var refMatrix = new Matrix4x4 {
            m00 = 1f - 2f * n.x * n.x,
            m01 = -2f * n.x * n.y,
            m02 = -2f * n.x * n.z,
            m03 = -2f * n.x * n.w,
            m10 = -2f * n.x * n.y,
            m11 = 1f - 2f * n.y * n.y,
            m12 = -2f * n.y * n.z,
            m13 = -2f * n.y * n.w,
            m20 = -2f * n.x * n.z,
            m21 = -2f * n.y * n.z,
            m22 = 1f - 2f * n.z * n.z,
            m23 = -2f * n.z * n.w,
            m30 = 0F,
            m31 = 0F,
            m32 = 0F,
            m33 = 1F
        };

        return refMatrix;
    }

    private void OnWillRenderObject() {
        // Mainカメラに映るときのみ反射描画を更新
        if (Camera.current != m_MainCamera) return;
        
        SetReflectionCamera();
        GL.invertCulling = true;
        m_RefCamera.Render();
        GL.invertCulling = false;
        m_MatRefPlane.SetTexture(m_RefTexId, m_RefTexture);
    }
}

MirrorReflection.shader

Shader "MirrorReflection"
{
	Properties
	{
		_ReflectionTex ("ReflectionTexture", 2D) = "white" {}
	}
	SubShader
	{
		Tags { "RenderType"="Opaque" }

		Pass
		{
			CGPROGRAM
			#pragma vertex vert
			#pragma fragment frag
			#include "UnityCG.cginc"

			struct appdata
			{
				float4 vertex : POSITION;
			};

			struct v2f
			{
				float4 vertex : SV_POSITION;
				float4 projCoord : TEXCOORD0;
			};
			
			sampler2D _ReflectionTex;
			
			v2f vert (appdata v)
			{
				v2f o;
				o.vertex = UnityObjectToClipPos(v.vertex);
				o.projCoord = ComputeScreenPos(o.vertex);
				return o;
			}
			
			fixed4 frag (v2f i) : SV_Target
			{
				// return tex2D(_ReflectionTex, i.projCoord.xy / i.projCoord.w);
				return tex2Dproj(_ReflectionTex, i.projCoord);
			}
			ENDCG
		}
	}
}

設定

「Plane」という名前のマテリアルを新規に作成して上記のシェーダーを割り当てます。

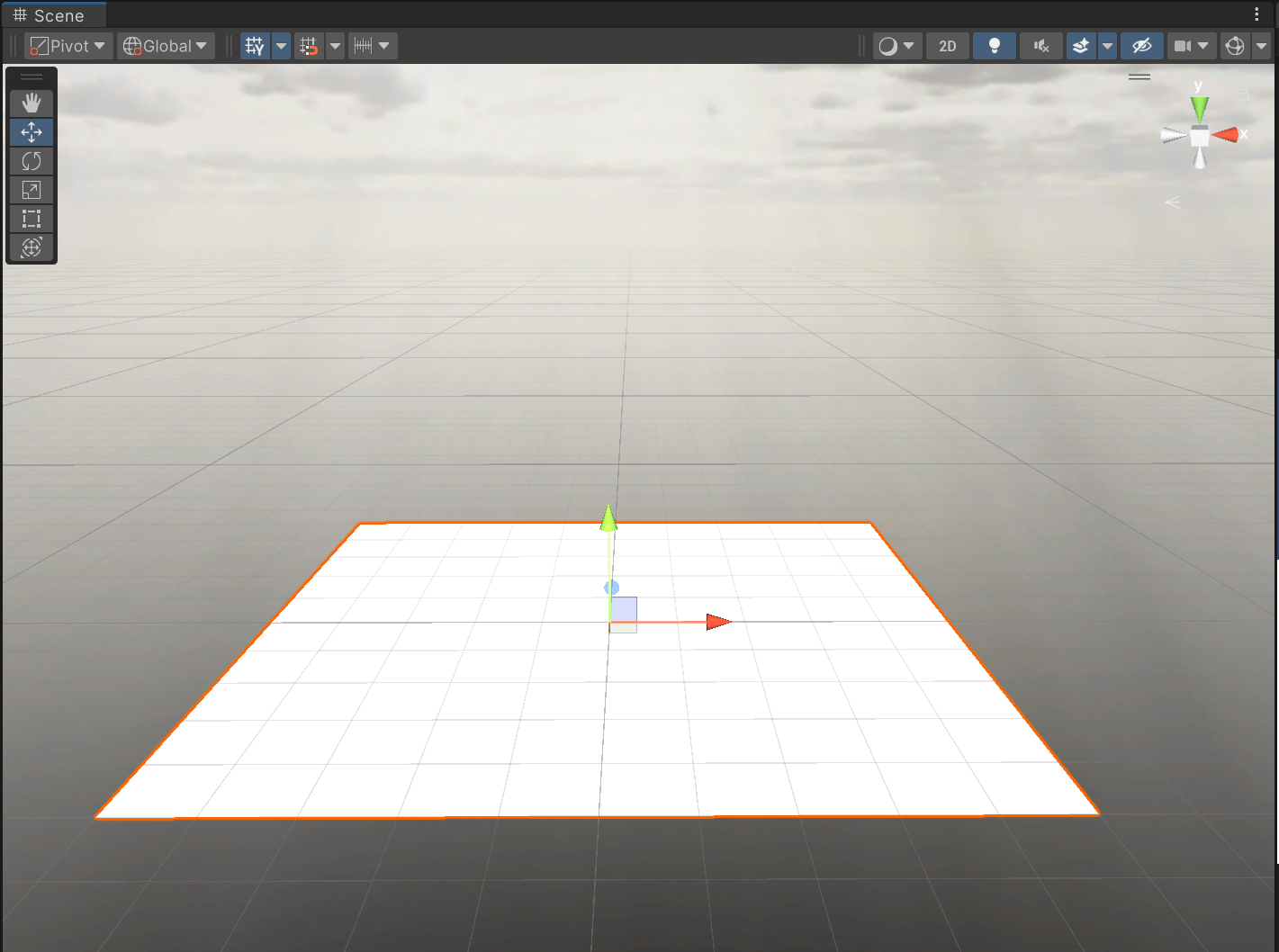
ヒエラルキー上で右クリック [3D Object] > [Plane]を選択してPlaneを配置します。

Planeオブジェクトをシーンに配置し、インスペクタから以下のように設定します。
①MirrorReflection.csをアタッチ(上記スクリプト)
②作成したPlaneマテリアルをアタッチ
③マテリアルにMirrorReflectionシェーダーが割り当てられていることを確認
④レイヤーにMirrorを追加してPlaneのオブジェクトに設定

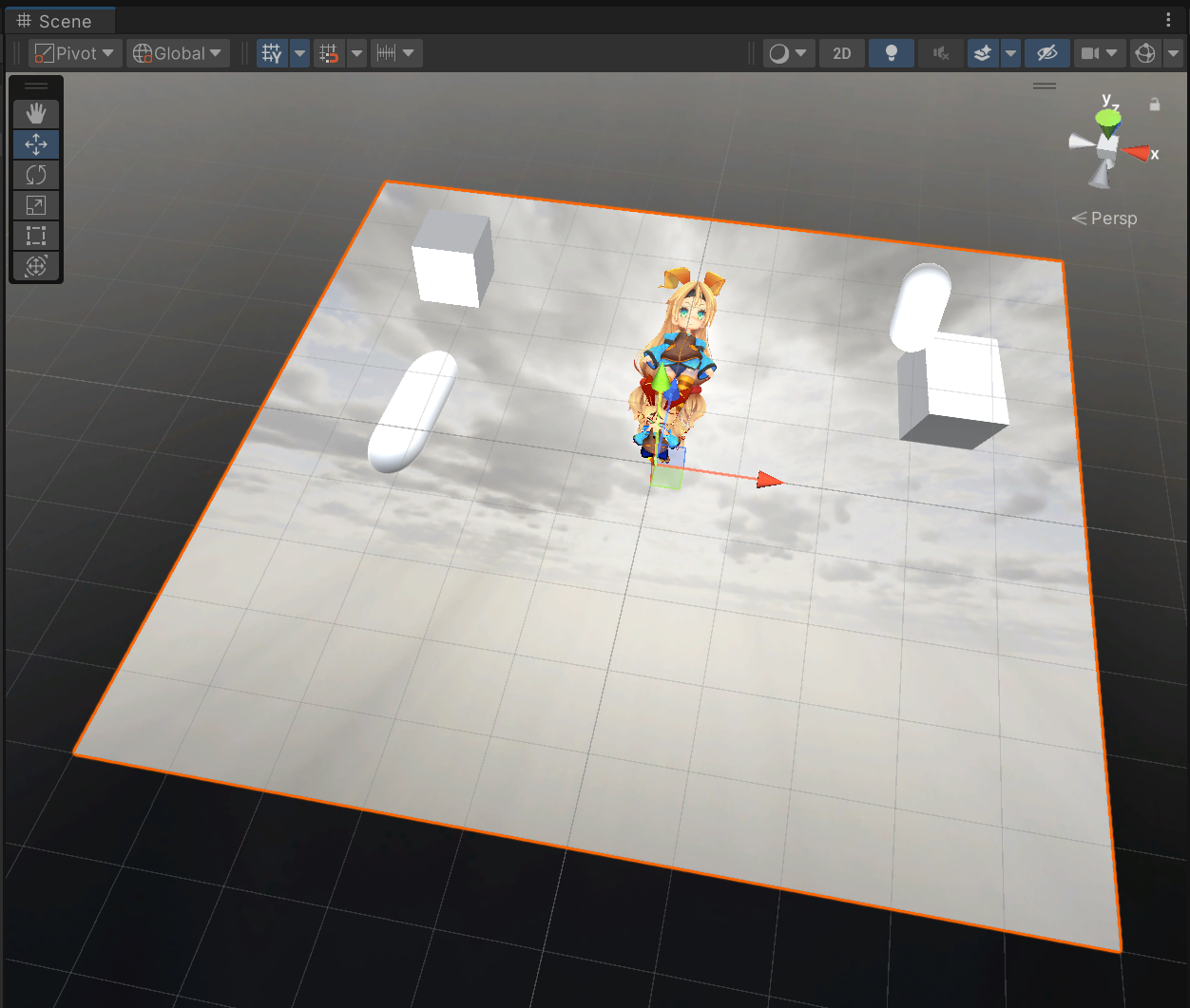
設定は以上で完了です。反射が分かりやすいようにPlane上に適当なオブジェクトを配置し、実行すると鏡面反射の効果を確認することができます。

このスクリプトでは随時、描画の更新を行っているためMainカメラの位置が変わっても破綻なく反射描画を再現することができます。

コード解説

ここからは順を追ってコードの解説を行っていきます。まずフィールド変数について。

private Camera m_MainCamera;
private Camera m_RefCamera;
private Material m_MatRefPlane;
private RenderTexture m_RefTexture;
private readonly int m_RefTexId = Shader.PropertyToID("_ReflectionTex");

型	変数	用途
Camera	m_MainCamera	GameViewに描画するMainカメラ
Camera	m_RefCamera	反射カメラ
Material	m_MatRefPlane	床のマテリアル
RenderTexture	m_RefTexture	床のテクスチャ
int	m_RefTexId	シェーダーで使用する床テクスチャ変数ID

m_RefTexIdはなくても構いませんが、床のテクスチャをマテリアルへ適用するときにstring型ではなくint型で指定すると処理負荷を抑えられます。

初期化

private void Start() {
    // 反射カメラの描画結果をTextureとして渡すためのRenderTexture
    m_RefTexture = new RenderTexture(Screen.width, Screen.height, 24, RenderTextureFormat.ARGB32);

    m_MainCamera = Camera.main;

    // 反射カメラをアタッチ
    m_RefCamera = gameObject.AddComponent<Camera>();
    // "Mirror"レイヤーを非表示
    m_RefCamera.cullingMask &= ~(1 << LayerMask.NameToLayer("Mirror"));
    m_RefCamera.enabled = false;
    m_RefCamera.hideFlags = HideFlags.HideAndDontSave;

    m_RefCamera.targetTexture = m_RefTexture;
    m_MatRefPlane = transform.GetComponent<Renderer>().sharedMaterial;
    m_MatRefPlane.SetTexture(m_RefTexId, m_RefTexture);
}

"Mirror"レイヤーのオブジェクト(=床)は映さないようにしています。

m_RefCamera.cullingMask &= ~(1 << LayerMask.NameToLayer("Mirror"));

m_RefCamera.enabled = falseで毎フレーム更新ではなく、負荷対策として後述する床がMainカメラに描画されるOnWillRenderObjectのタイミングで描画更新を行うようにします。また、反射カメラはスクリプトのみによる動的制御にするため、HideAndDontSaveに設定してインスペクタからは変更できないようにします。

m_RefCamera.enabled = false;
m_RefCamera.hideFlags = HideFlags.HideAndDontSave;

反射カメラの描画

床がMainカメラに描画されるタイミングで実行されます。ここからは数学の知識が必要になります。

private void SetReflectionCamera() {
    // 平面の方程式を作成
    Vector3 planeNormal = transform.up;
    Vector3 planePos = transform.position;
    float d = -Vector3.Dot(planeNormal, planePos);
    // 反射行列の生成
    Matrix4x4 refMatrix = CalcReflectionMatrix(new Vector4(planeNormal.x, planeNormal.y, planeNormal.z, d));
    // メインカメラの座標と反射行列を使って反射カメラの座標を代入
    m_RefCamera.worldToCameraMatrix = m_MainCamera.worldToCameraMatrix * refMatrix;

    // 床の下を貫通するオブジェクトを表示させないようにクリッピング
    Vector3 cPos = m_RefCamera.worldToCameraMatrix.MultiplyPoint(planePos);
    Vector3 cNormal = m_RefCamera.worldToCameraMatrix.MultiplyVector(planeNormal).normalized;
    Vector4 clipPlane = new Vector4(cNormal.x, cNormal.y, cNormal.z, -Vector3.Dot(cPos, cNormal));
    
    m_RefCamera.projectionMatrix = m_MainCamera.CalculateObliqueMatrix(clipPlane);
}

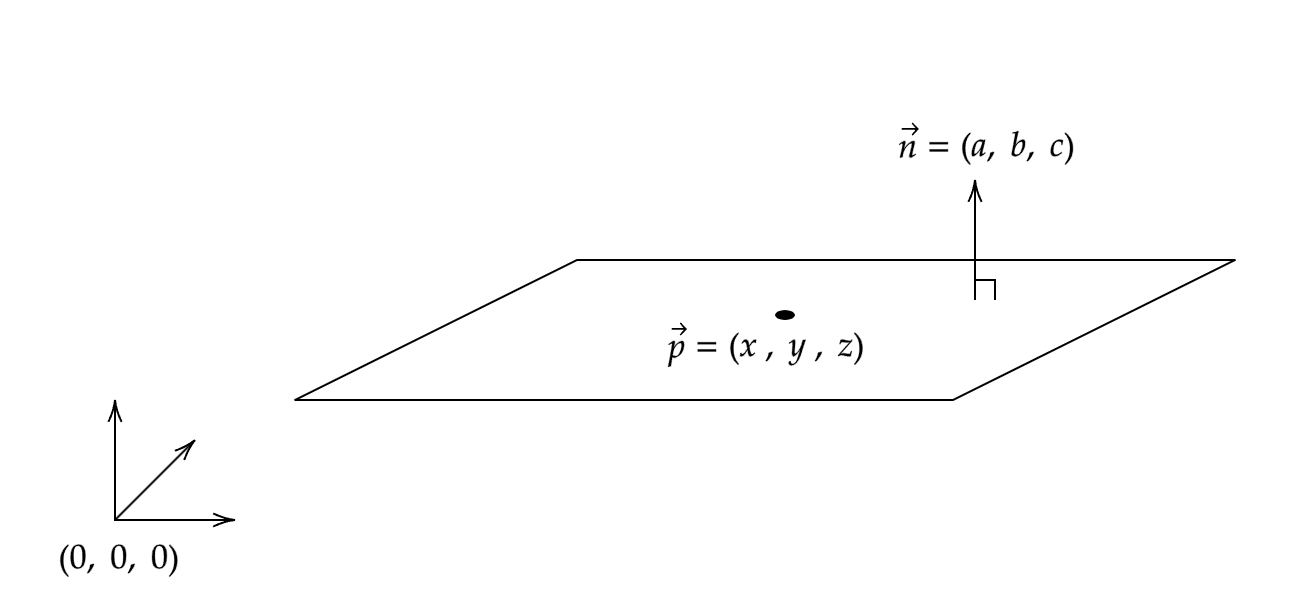
まず、平面床を基準とした反射位置を計算するために平面の方程式を作ります。平面上の座標ベクトルを $\vec{p} =( x,\ y,\ z)$ 、平面の法線ベクトルを $\vec{n} =( a,\ b,\ c)$ とすると平面の方程式は以下で表されます。

ax+by+cz+d=0

これを $d$ の式で表すと以下の通りになります。

-d=ax+by+cz

右辺を行列、ベクトル式で表すと

\begin{aligned}
ax+by+cz & =\begin{pmatrix}
a & b & c
\end{pmatrix}\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}\\
 & =\vec{n} \cdot \vec{p}
\end{aligned}

整理すると $d$ は次式で表されます。

d=-\vec{n} \cdot \vec{p}

これらの結果を使って平面の成分ベクトル Vector4(a, b, c, d) を作ります。

Vector3 planeNormal = transform.up;// 平面の法線
Vector3 planePos = transform.position;// 平面の位置ベクトル
float d = -Vector3.Dot(planeNormal, planePos);// 法線と位置ベクトルの内積
var plane = new Vector4(planeNormal.x, planeNormal.y, planeNormal.z, d)// 平面のベクトル成分

次に空間座標を反転させるための反射行列を作成します。Mainカメラのベクトルを$\vec{a}$、反射カメラのベクトルを$\vec{b}$、平面床の法線ベクトルを$\vec{n}$、Mainカメラから平面床に向かって下した垂線ベクトルを$\vec{c}$、$\vec{a}$と$\vec{c}$のなす角を$\theta$として図に示します。

このとき、$\vec{b}$は次式で表されます。

\vec{b} =\vec{a} +2\vec{c}

$\vec{c}$と平面床の法線ベクトル$\vec{n}$は逆向きのベクトルであるため、それぞれの単一ベクトルの関係式は

\frac{\vec{c}}{|\vec{c} |} =-\frac{\vec{n}}{|\vec{n} |}

となり、

|\vec{c} |=|\vec{a} |\cos \theta

と合わせて$\vec{b}$を表すと以下のようになります。

\begin{aligned}
\vec{b} & =\vec{a} +2\vec{c}\\
 & =\vec{a} -2\frac{\vec{n}}{|\vec{n} |} |\vec{c} |\\
 & =\vec{a} -2\frac{\vec{n}}{|\vec{n} |} |\vec{a} |\cos \theta 
\end{aligned}

これで式から$\vec{c}$を消すことができました。さらに内積の公式より

\vec{n} \cdot \vec{a} =|\vec{n} ||\vec{a} |\cos \theta

|\vec{a} |\cos \theta =\frac{\vec{n} \cdot \vec{a}}{|\vec{n} |}

これを$\vec{b}$式に代入し、平面の法線ベクトルの大きさ$|\vec{n} |=1$のとき次式が得られます。

\begin{aligned}
\vec{b} & =\vec{a} -2\frac{\vec{n}}{|\vec{n} |} |\vec{a} |\cos \theta \\
 & =\vec{a} -2\frac{\vec{n}}{|\vec{n} |}\frac{\vec{n} \cdot \vec{a}}{|\vec{n} |}\\
 & =\vec{a} -2\vec{n}\frac{\vec{n} \cdot \vec{a}}{|\vec{n} |^{2}}\\
 & =\vec{a} -2(\vec{n} \cdot \vec{a})\vec{n}\\
 & =( 1-2\vec{n}\vec{n})\vec{a}
\end{aligned}

$\vec{a}$の係数を抜き出して行列式に置き換えると

\begin{aligned}
( 1-2\vec{n}\vec{n}) & =I-2NN^{T}\\
 & =R
\end{aligned}

となりワールド空間における平面反射変換行列$R$が得られます。

R=I-2NN^{T}

平面方程式の成分を$\vec{n} =( n_{x} ,\ n_{y} ,\ n_{z} ,\ n_{w})$として、この変換行列を単一の行列に置き換えると平面反射変換行列$R$は以下のようになります。

\begin{aligned}
I-2NN^{T} & =\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix} -2\begin{pmatrix}
n_{x}\\
n_{y}\\
n_{z}\\
n_{w}
\end{pmatrix}\begin{pmatrix}
n_{x} & n_{y} & n_{z} & n_{w}
\end{pmatrix}\\
 & =\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix} -2\begin{pmatrix}
n_{x}^{2} & n_{x} n_{y} & n_{x} n_{z} & n_{x} n_{w}\\
n_{x} n_{y} & n_{y}^{2} & n_{y} n_{z} & n_{y} n_{w}\\
n_{x} n_{z} & n_{y} n_{z} & n_{z}^{2} & n_{z} n_{w}\\
n_{x} n_{w} & n_{y} n_{w} & n_{z} n_{w} & n_{w}^{2}
\end{pmatrix}\\
 & =\begin{pmatrix}
1-2n_{x}^{2} & -2n_{x} n_{y} & -2n_{x} n_{z} & -2n_{x} n_{w}\\
-2n_{x} n_{y} & 1-2n_{y}^{2} & -2n_{y} n_{z} & -2n_{y} n_{w}\\
-2n_{x} n_{z} & -2n_{y} n_{z} & 1-2n_{z}^{2} & -2n_{z} n_{w}\\
-2n_{x} n_{w} & -2n_{y} n_{w} & -2n_{z} n_{w} & 1-2n_{w}^{2}
\end{pmatrix}
\end{aligned}

この行列は3次元空間における反射のアフィン変換となるため、4行目は使用せず対角成分だけ残すと最終的な平面の反射行列$R$は次式となります。

R=\begin{pmatrix}
1-2n_{x}^{2} & -2n_{x} n_{y} & -2n_{x} n_{z} & -2n_{x} n_{w}\\
-2n_{x} n_{y} & 1-2n_{y}^{2} & -2n_{y} n_{z} & -2n_{y} n_{w}\\
-2n_{x} n_{z} & -2n_{y} n_{z} & 1-2n_{z}^{2} & -2n_{z} n_{w}\\
0 & 0 & 0 & 1
\end{pmatrix}

長い道のりでしたが、これをUnityのMatrix4x4のコードに置き換えたものが以下になります。

M_{matrix4x4} =\begin{pmatrix}
m00 & m01 & m02 & m03\\
m10 & m11 & m12 & m13\\
m20 & m21 & m22 & m23\\
m30 & m31 & m32 & m33
\end{pmatrix}

private Matrix4x4 CalcReflectionMatrix(Vector4 n) {
    var refMatrix = new Matrix4x4 {
        m00 = 1f - 2f * n.x * n.x,
        m01 = -2f * n.x * n.y,
        m02 = -2f * n.x * n.z,
        m03 = -2f * n.x * n.w,
        m10 = -2f * n.x * n.y,
        m11 = 1f - 2f * n.y * n.y,
        m12 = -2f * n.y * n.z,
        m13 = -2f * n.y * n.w,
        m20 = -2f * n.x * n.z,
        m21 = -2f * n.y * n.z,
        m22 = 1f - 2f * n.z * n.z,
        m23 = -2f * n.z * n.w,
        m30 = 0F,
        m31 = 0F,
        m32 = 0F,
        m33 = 1F
    };

    return refMatrix;
}

生成した反射行列はworldToCameraMatrixと掛け合わせて代入します。右から反射行列を掛けている理由としては、ワールド空間座標における反射行列を反射カメラのビュー行列に変換しているというように私は解釈しています。この辺りは、前回の記事で検証を行っているので参考にしてみてください。

// 反射行列の生成
Matrix4x4 refMatrix = CalcReflectionMatrix(plane);
// ワールド空間の反射行列を反射カメラのビュー行列で変換して代入
m_RefCamera.worldToCameraMatrix = m_MainCamera.worldToCameraMatrix * refMatrix;

また、以下のコードで反射カメラと平面床との間をクリッピングすることで床を貫通したオブジェクトを非表示にしています。

// 床の下を貫通するオブジェクトを表示させないようにクリッピング
Vector3 cPos = m_RefCamera.worldToCameraMatrix.MultiplyPoint(planePos);
Vector3 cNormal = m_RefCamera.worldToCameraMatrix.MultiplyVector(planeNormal).normalized;
Vector4 clipPlane = new Vector4(cNormal.x, cNormal.y, cNormal.z, -Vector3.Dot(cPos, cNormal));

m_RefCamera.projectionMatrix = m_MainCamera.CalculateObliqueMatrix(clipPlane);

// クリッピングしない場合(床貫通オブジェクト表示)
// m_RefCamera.projectionMatrix = m_MainCamera.projectionMatrix;

クリップしない場合

クリップする場合

最後にOnWillRenderObjectでMainカメラから床が描画されたときに以下のコードが実行されます。

private void OnWillRenderObject() {
    // Mainカメラに映るときのみ反射描画を更新
    if (Camera.current != m_MainCamera) return;
    
    SetReflectionCamera();
    GL.invertCulling = true;
    m_RefCamera.Render();
    GL.invertCulling = false;
    m_MatRefPlane.SetTexture(m_RefTexId, m_RefTexture);
}

反射カメラのビュー行列ではポリゴンの面の向きが変わるため裏面表示されます。そのためGL.invertCullingを使ってCullingの扱いを反転させてからレンダリングし、その後元に戻しています。レンダリング後は描画結果をマテリアルに渡してC#側の処理は完了です。

シェーダー

シェーダー側は、ComputeScreenPosで床の頂点をスクリーン座標に変換します。

o.projCoord = ComputeScreenPos(o.vertex);

その後、反射カメラの描画結果を_ReflectionTexで受け取り、スクリーン座標を基に投影テクスチャマッピング(tex2Dproj)で描画します。手動で行う場合はprojCoord.wで除算します。

fixed4 frag (v2f i) : SV_Target
{
    // return tex2D(_ReflectionTex, i.projCoord.xy / i.projCoord.w);
    return tex2Dproj(_ReflectionTex, i.projCoord);
}

単純にuvでtex2Dサンプリングすると以下のように正しい描画にはなりません。

意図する描画

おわりに

ここまで数学の知識を交えながら鏡面反射の仕組みをみてきました。Planar Reflectionは同じ反射を表現する仕組みのScreen Space Reflection(SSR)と比較すると高品質ではあるものの、高負荷になりがちです。

冒頭で触れた通りPlanar Reflectionの仕組みをしっかりと理解した上で使いこなしたいという思いからこの記事を書きました。記事を書き終わった今、理解は進んだものの、私自身まだ「完全に理解した」とは言えませんが、皆様にとってこの記事が少しでも鏡面反射の仕組みを理解する手助けになれば幸いです。🌱

参考リンク

今回の記事作成では様々なサイトを参考にさせていただきました。改めてこの場をお借りしてお礼申し上げます。

https://karanokan.info/2018/10/17/post-1284/
https://community.arm.com/arm-community-blogs/b/graphics-gaming-and-vr-blog/posts/combined-reflections-stereo-reflections-in-vr
https://gamedev.stackexchange.com/questions/43615/how-can-i-reflect-a-point-with-respect-to-the-plane/43692
https://math.stackexchange.com/questions/693414/reflection-across-the-plane
https://en.wikipedia.org/wiki/Transformation_matrix#Reflection_2
https://github.com/Unity-Technologies/BoatAttack/blob/master/Packages/com.verasl.water-system/Scripts/Rendering/PlanarReflections.cs
https://github.com/unity3d-jp/unitychan-crs/blob/master/Assets/UnityChanStage/Visualizer/MirrorReflection.cs
http://blog.livedoor.jp/take_z_ultima/archives/51754969.html
https://inarijuku-online.com/blog/20230612-1351/
https://manabitimes.jp/math/679
https://light11.hatenadiary.com/entry/2018/06/13/235543

使用モデルのライセンス

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up