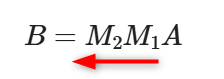行列の世界
行列を用いて座標変換を行うことができることは知られていますが、クォータニオンやベクトルと比較するとパラメータ数が多い行列はあまり使用されません。しかしながら、カメラの描画周りでは行列を扱う場面が稀にあり行列の特徴や特性を理解することでより幅広い演出が可能になります。
Unityで行列を扱うにはMatrix4x4クラスを使用します。ここでは、Unityで行列を少しでも扱えるようにネットの記事やUnity公式リファレンスと照らし合わせながら、Matrix4x4クラスの謎を紐解いていきます。
行オーダーと列オーダー
行列演算を行うとき、最初に立ちはだかる壁が行列の掛け算(積)です。行列は掛け算の順序によって結果が異なることを学びますが、Unityの世界ではどの順番で掛けるのが正しいのでしょうか。まずネットで調べてみるとコンピューターグラフィックスでは行列を扱うときに、プラットフォームによって行オーダーか列オーダーが定義されており、どちらで採用されているかで掛け算の順序が変わるようです。
行オーダー
\begin{pmatrix}
x' & y' & z' & 1
\end{pmatrix} =\begin{pmatrix}
x & y & z & 1
\end{pmatrix} \times \begin{pmatrix}
mat[ 0] & mat[ 1] & mat[ 2] & mat[ 3]\\
mat[ 4] & mat[ 5] & mat[ 6] & mat[ 7]\\
mat[ 8] & mat[ 9] & mat[ 10] & mat[ 11]\\
mat[ 12] & mat[ 13] & mat[ 14] & mat[ 15]
\end{pmatrix}
列オーダー
\begin{pmatrix}
x'\\
y'\\
z'\\
1
\end{pmatrix} =\begin{pmatrix}
mat[0] & mat[4] & mat[8] & mat[12] \\
mat[1] & mat[5] & mat[9] & mat[13] \\
mat[2] & mat[6] & mat[10] & mat[14]\\
mat[3] & mat[7] & mat[11] & mat[15]
\end{pmatrix} \times \begin{pmatrix}
x\\
y\\
z\\
1
\end{pmatrix}
なるほど、なるほど...
行オーダーであれば変換行列を右、列オーダーであれば左から掛ければよさそうです。
ではUnityではどうでしょうか。以下のコードを実行してみます。
private void Start() {
var matrix = new Matrix4x4 {
[0] = 0,
[1] = 1,
[2] = 2,
[3] = 3,
[4] = 4,
[5] = 5,
[6] = 6,
[7] = 7,
[8] = 8,
[9] = 9,
[10] = 10,
[11] = 11,
[12] = 12,
[13] = 13,
[14] = 14,
[15] = 15
};
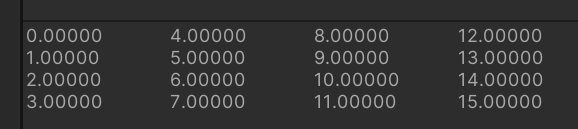
Debug.Log(matrix);
}
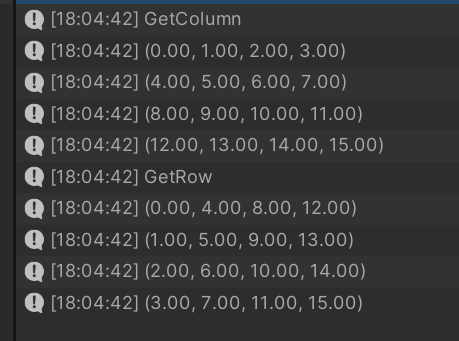
Matrix4x4には列と行をインデックスで指定して取得するメソッド(GetColumn/GetRow)があるので念のため確認してみます。
Debug.Log("GetColumn");
Debug.Log(matrix.GetColumn(0));// (0.00, 1.00, 2.00, 3.00)
Debug.Log(matrix.GetColumn(1));// (4.00, 5.00, 6.00, 7.00)
Debug.Log(matrix.GetColumn(2));// (8.00, 9.00, 10.00, 11.00)
Debug.Log(matrix.GetColumn(3));// (12.00, 13.00, 14.00, 15.00)
Debug.Log("GetRow");
Debug.Log(matrix.GetRow(0));// (0.00, 4.00, 8.00, 12.00)
Debug.Log(matrix.GetRow(1));// (1.00, 5.00, 9.00, 13.00)
Debug.Log(matrix.GetRow(2));// (2.00, 6.00, 10.00, 14.00)
Debug.Log(matrix.GetRow(3));// (3.00, 7.00, 11.00, 15.00)
結果よりUnityは列オーダーの雰囲気を感じます。
ではもう少し踏み込んでUnity社が公開しているMatrix4x4のC#リファレンスを確認してみます。
Matrix4x4には各成分をmXXで指定してアクセスできるプロパティが用意されており、演算はこのプロパティを介して行われています。では先ほど確認した配列の成分がどのように対応しているかをコードから読み解くと以下の通りになっていました。
\begin{pmatrix}
m00 & m01 & m02 & m03\\
m10 & m11 & m12 & m13\\
m20 & m21 & m22 & m23\\
m30 & m31 & m32 & m33
\end{pmatrix} =\begin{pmatrix}
mat[ 0] & mat[ 4] & mat[ 8] & mat[ 12]\\
mat[ 1] & mat[ 5] & mat[ 9] & mat[ 13]\\
mat[ 2] & mat[ 6] & mat[ 10] & mat[ 14]\\
mat[ 3] & mat[ 7] & mat[ 11] & mat[ 15]
\end{pmatrix}
実行して確認してみました。
private void Start() {
var matrix = new Matrix4x4 {
[0] = 0,
[1] = 1,
[2] = 2,
[3] = 3,
[4] = 4,
[5] = 5,
[6] = 6,
[7] = 7,
[8] = 8,
[9] = 9,
[10] = 10,
[11] = 11,
[12] = 12,
[13] = 13,
[14] = 14,
[15] = 15
};
Debug.Log($"{matrix.m00}, {matrix.m10}, {matrix.m20}, {matrix.m30}, " +
$"{matrix.m01}, {matrix.m11}, {matrix.m21}, {matrix.m31}, " +
$"{matrix.m02}, {matrix.m12}, {matrix.m22}, {matrix.m32}, " +
$"{matrix.m03}, {matrix.m13}, {matrix.m23}, {matrix.m33}");
}
しかし、公式リファレンスの冒頭には気になる記述を見つけることができます。
https://github.com/Unity-Technologies/UnityCsReference/blob/cc8ba043128e585c40ce3e1de4d745a3407e129e/Runtime/Export/Math/Matrix4x4.cs#L23-L33

(実際のコードと並びが違うぞ?...![]() それに
それに *undocumented* ...?)
\begin{pmatrix}
m00 & m01 & m02 & m03\\
m10 & m11 & m12 & m13\\
m20 & m21 & m22 & m23\\
m30 & m31 & m32 & m33
\end{pmatrix} =\begin{pmatrix}
mat[ 0] & mat[ 4] & mat[ 8] & mat[ 12]\\
mat[ 1] & mat[ 5] & mat[ 9] & mat[ 13]\\
mat[ 2] & mat[ 6] & mat[ 10] & mat[ 14]\\
mat[ 3] & mat[ 7] & mat[ 11] & mat[ 15]
\end{pmatrix}
とりあえず次のステップに進みます。
掛け算オペレーター
配列の成分が確認できたので、次は実際に掛け算の処理を見てみます。Matrix4x4では積のオペレーターが定義されておりリファレンスより以下のようになっています。
// Multiplies two matrices.
public static Matrix4x4 operator*(Matrix4x4 lhs, Matrix4x4 rhs)
{
Matrix4x4 res;
res.m00 = lhs.m00 * rhs.m00 + lhs.m01 * rhs.m10 + lhs.m02 * rhs.m20 + lhs.m03 * rhs.m30;
res.m01 = lhs.m00 * rhs.m01 + lhs.m01 * rhs.m11 + lhs.m02 * rhs.m21 + lhs.m03 * rhs.m31;
res.m02 = lhs.m00 * rhs.m02 + lhs.m01 * rhs.m12 + lhs.m02 * rhs.m22 + lhs.m03 * rhs.m32;
res.m03 = lhs.m00 * rhs.m03 + lhs.m01 * rhs.m13 + lhs.m02 * rhs.m23 + lhs.m03 * rhs.m33;
res.m10 = lhs.m10 * rhs.m00 + lhs.m11 * rhs.m10 + lhs.m12 * rhs.m20 + lhs.m13 * rhs.m30;
res.m11 = lhs.m10 * rhs.m01 + lhs.m11 * rhs.m11 + lhs.m12 * rhs.m21 + lhs.m13 * rhs.m31;
res.m12 = lhs.m10 * rhs.m02 + lhs.m11 * rhs.m12 + lhs.m12 * rhs.m22 + lhs.m13 * rhs.m32;
res.m13 = lhs.m10 * rhs.m03 + lhs.m11 * rhs.m13 + lhs.m12 * rhs.m23 + lhs.m13 * rhs.m33;
res.m20 = lhs.m20 * rhs.m00 + lhs.m21 * rhs.m10 + lhs.m22 * rhs.m20 + lhs.m23 * rhs.m30;
res.m21 = lhs.m20 * rhs.m01 + lhs.m21 * rhs.m11 + lhs.m22 * rhs.m21 + lhs.m23 * rhs.m31;
res.m22 = lhs.m20 * rhs.m02 + lhs.m21 * rhs.m12 + lhs.m22 * rhs.m22 + lhs.m23 * rhs.m32;
res.m23 = lhs.m20 * rhs.m03 + lhs.m21 * rhs.m13 + lhs.m22 * rhs.m23 + lhs.m23 * rhs.m33;
res.m30 = lhs.m30 * rhs.m00 + lhs.m31 * rhs.m10 + lhs.m32 * rhs.m20 + lhs.m33 * rhs.m30;
res.m31 = lhs.m30 * rhs.m01 + lhs.m31 * rhs.m11 + lhs.m32 * rhs.m21 + lhs.m33 * rhs.m31;
res.m32 = lhs.m30 * rhs.m02 + lhs.m31 * rhs.m12 + lhs.m32 * rhs.m22 + lhs.m33 * rhs.m32;
res.m33 = lhs.m30 * rhs.m03 + lhs.m31 * rhs.m13 + lhs.m32 * rhs.m23 + lhs.m33 * rhs.m33;
return res;
}
式を確認すると通常の行列の掛け算として定義されていることがわかります。
\begin{aligned}
AB & =\begin{pmatrix}
a_{00} & a_{01} & a_{02} & a_{03}\\
a_{10} & a_{11} & a_{12} & a_{13}\\
a_{20} & a_{21} & a_{22} & a_{23}\\
a_{30} & a_{31} & a_{32} & a_{33}
\end{pmatrix}\begin{pmatrix}
b_{00} & b_{01} & b_{02} & b_{03}\\
b_{10} & b_{11} & b_{12} & b_{13}\\
b_{20} & b_{21} & b_{22} & b_{23}\\
b_{30} & b_{31} & b_{32} & b_{33}
\end{pmatrix}\\
& \\
& =\begin{pmatrix}
a_{00} b_{00} +a_{01} b_{10} +a_{02} b_{20} +a_{03} b_{30} & a_{00} b_{01} +a_{01} b_{11} +a_{02} b_{21} +a_{03} b_{31} & a_{00} b_{02} +a_{01} b_{12} +a_{02} b_{22} +a_{03} b_{32} & a_{00} b_{03} +a_{01} b_{13} +a_{02} b_{23} +a_{03} b_{33}\\
a_{10} b_{00} +a_{11} b_{10} +a_{12} b_{20} +a_{13} b_{30} & a_{10} b_{01} +a_{11} b_{11} +a_{12} b_{21} +a_{13} b_{31} & a_{10} b_{02} +a_{11} b_{12} +a_{12} b_{22} +a_{13} b_{32} & a_{10} b_{03} +a_{11} b_{13} +a_{12} b_{23} +a_{13} b_{33}\\
a_{20} b_{00} +a_{21} b_{10} +a_{22} b_{20} +a_{23} b_{30} & a_{20} b_{01} +a_{21} b_{11} +a_{22} b_{21} +a_{23} b_{31} & a_{20} b_{02} +a_{21} b_{12} +a_{22} b_{22} +a_{23} b_{32} & a_{20} b_{03} +a_{21} b_{13} +a_{22} b_{23} +a_{23} b_{33}\\
a_{30} b_{00} +a_{31} b_{10} +a_{32} b_{20} +a_{33} b_{30} & a_{30} b_{01} +a_{31} b_{11} +a_{32} b_{21} +a_{33} b_{31} & a_{30} b_{02} +a_{31} b_{12} +a_{32} b_{22} +a_{33} b_{32} & a_{30} b_{03} +a_{31} b_{13} +a_{32} b_{23} +a_{33} b_{33}
\end{pmatrix}
\end{aligned}
以上を踏まえるとUnityの行列の掛け算は通常の行列の掛け算として扱っても問題なさそうです。次は行列成分の意味をみていきます。
ベクトルと行列成分
行列成分の前に2次元のベクトル式についておさらいします。
平行移動
$x, y$軸方向に$t_{x}, t_{y}$移動
\begin{array}{l}
x'=x+t_{x}
\\
y'=y+t_{y}
\end{array}
スケール
$x, y$軸方向に$s_{x}, s_{y}$移動
\begin{array}{l}
x'=s_{x}x
\\
y'=s_{y}y
\end{array}
回転
原点を中心に角度$\theta$回転
\begin{array}{l}
x'=x\cos \theta -y\sin \theta \\
y'=x\sin \theta +y\cos \theta
\end{array}
これらを行列とベクトルの関係式で表すと以下の通りになります。
平行移動
\begin{pmatrix}
x'\\
y'
\end{pmatrix} =\begin{pmatrix}
x\\
y
\end{pmatrix} +\begin{pmatrix}
t_{x}\\
t_{y}
\end{pmatrix} =\begin{pmatrix}
x+t_{x}\\
y+t_{y}
\end{pmatrix}
スケール
\begin{pmatrix}
x'\\
y'
\end{pmatrix} =\begin{pmatrix}
s_{x} & 0\\
0 & s_{y}
\end{pmatrix}\begin{pmatrix}
x\\
y
\end{pmatrix} =\begin{pmatrix}
s_{x} x\\
s_{y} y
\end{pmatrix}
回転
\begin{pmatrix}
x'\\
y'
\end{pmatrix} =\begin{pmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix}\begin{pmatrix}
x\\
y
\end{pmatrix} =\begin{pmatrix}
x\cos \theta -y\sin \theta \\
x\sin \theta +y\cos \theta
\end{pmatrix}
さらに3次元に拡張して4x4行列として表すと以下の通りになります。
平行移動
\begin{pmatrix}
x'\\
y'\\
z'\\
1
\end{pmatrix} =\begin{pmatrix}
1 & 0 & 0 & t_{x}\\
0 & 1 & 0 & t_{y}\\
0 & 0 & 1 & t_{z}\\
0 & 0 & 0 & 1
\end{pmatrix}\begin{pmatrix}
x\\
y\\
z\\
1
\end{pmatrix} =\begin{pmatrix}
x+t_{x}\\
y+t_{y}\\
z+t_{z}\\
1
\end{pmatrix}
スケール
\begin{pmatrix}
x'\\
y'\\
z'\\
1
\end{pmatrix} =\begin{pmatrix}
s_{x} & 0 & 0 & 0\\
0 & s_{y} & 0 & 0\\
0 & 0 & s_{z} & 0\\
0 & 0 & 0 & 1
\end{pmatrix}\begin{pmatrix}
x\\
y\\
z\\
1
\end{pmatrix} =\begin{pmatrix}
s_{x} x\\
s_{y} y\\
s_{z} z\\
1
\end{pmatrix}
回転
$x$軸まわりの回転
\begin{pmatrix}
x'\\
y'\\
z'\\
1
\end{pmatrix} =\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & \cos \theta & -\sin \theta & 0\\
0 & \sin \theta & \cos \theta & 0\\
0 & 0 & 0 & 1
\end{pmatrix}\begin{pmatrix}
x\\
y\\
z\\
1
\end{pmatrix} =\begin{pmatrix}
x\\
y\cos \theta -\sin \theta \\
y\sin \theta +\cos \theta \\
1
\end{pmatrix}
$y$軸まわりの回転
\begin{pmatrix}
x'\\
y'\\
z'\\
1
\end{pmatrix} =\begin{pmatrix}
\cos \theta & 0 & \sin \theta & 0\\
0 & 1 & 0 & 0\\
-\sin \theta & 0 & \cos \theta & 0\\
0 & 0 & 0 & 1
\end{pmatrix}\begin{pmatrix}
x\\
y\\
z\\
1
\end{pmatrix} =\begin{pmatrix}
x\cos \theta +z\sin \theta \\
y\\
-x\sin \theta +z\cos \theta \\
1
\end{pmatrix}
$z$軸まわりの回転
\begin{pmatrix}
x'\\
y'\\
z'\\
1
\end{pmatrix} =\begin{pmatrix}
\cos \theta & -\sin \theta & 0 & 0\\
\sin \theta & \cos \theta & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix}\begin{pmatrix}
x\\
y\\
z\\
1
\end{pmatrix} =\begin{pmatrix}
x\cos \theta -\sin \theta \\
x\sin +y\cos \theta \\
z\\
1
\end{pmatrix}
このように座標を変換するには、変換行列と元の座標(3次元ベクトル)との積で求めることができます。また、変換行列に掛ける3次元ベクトルを回転、スケールと組み合わせた4x4行列とした場合も同様に変換行列の式が成り立ちます。
変換行列をA、変換前の行列をB、変換後の行列をCとすると以下のようになります。
\begin{aligned}
C & =AB\\
\begin{pmatrix}
c_{00} & c_{01} & c_{02} & c_{03}\\
c_{10} & c_{11} & c_{12} & c_{13}\\
c_{20} & c_{21} & c_{22} & c_{23}\\
c_{30} & c_{31} & c_{32} & c_{33}
\end{pmatrix} & =\begin{pmatrix}
a_{00} & a_{01} & a_{02} & a_{03}\\
a_{10} & a_{11} & a_{12} & a_{13}\\
a_{20} & a_{21} & a_{22} & a_{23}\\
a_{30} & a_{31} & a_{32} & a_{33}
\end{pmatrix}\begin{pmatrix}
b_{00} & b_{01} & b_{02} & b_{03}\\
b_{10} & b_{11} & b_{12} & b_{13}\\
b_{20} & b_{21} & b_{22} & b_{23}\\
b_{30} & b_{31} & b_{32} & b_{33}
\end{pmatrix}
\end{aligned}
UnityのTransformからMatrix4x4を作成するにはMatrix4x4.TRSやTransform.localToWorldMatrixなどの便利なメソッドとプロパティが用意されているため、変換行列との積の式を作る場合はこれを利用します。
Matrix4x4 matrix1 = Matrix4x4.TRS(transform.position, transform.rotation, transform.localScale);
Matrix4x4 matrix2 = transform.localToWorldMatrix;
変換行列の成分と演算式の作り方がわかってきたところで、実際のコードで確認してみます。
平行移動
public class TransformMatrix : MonoBehaviour {
[SerializeField] private Transform m_Target;
private void Start() {
var pos = new Vector3(1, 0.5f, -1.2f);
var posMatrix = new Matrix4x4 {
m00 = 1,
m01 = 0,
m02 = 0,
m03 = pos.x,
m10 = 0,
m11 = 1,
m12 = 0,
m13 = pos.y,
m20 = 0,
m21 = 0,
m22 = 1,
m23 = pos.z,
m30 = 0,
m31 = 0,
m32 = 0,
m33 = 1
};
var matrix = posMatrix * m_Target.localToWorldMatrix;
// m_Target.position = new Vector3(matrix.m03, matrix.m13, matrix.m23);
m_Target.position = matrix.GetPosition();
}
}
スケール
public class ScaleMatrix : MonoBehaviour {
[SerializeField] private Transform m_Target;
private void Start() {
var scale = new Vector3(2, 2, 2);
var scaleMatrix = new Matrix4x4 {
m00 = scale.x,
m01 = 0,
m02 = 0,
m03 = 0,
m10 = 0,
m11 = scale.y,
m12 = 0,
m13 = 0,
m20 = 0,
m21 = 0,
m22 = scale.z,
m23 = 0,
m30 = 0,
m31 = 0,
m32 = 0,
m33 = 1
};
var matrix = scaleMatrix * m_Target.localToWorldMatrix;
m_Target.localScale = matrix.lossyScale;
}
}
回転(Y軸)
public class RotationMatrix : MonoBehaviour {
[SerializeField] private Transform m_Target;
private void Start() {
var rot = Mathf.Deg2Rad * 30;
// Y軸で回転
var rotMatrix = new Matrix4x4 {
m00 = Mathf.Cos(rot),
m01 = 0,
m02 = Mathf.Sin(rot),
m03 = 0,
m10 = 0,
m11 = 1,
m12 = 0,
m13 = 0,
m20 = -Mathf.Sin(rot),
m21 = 0,
m22 = Mathf.Cos(rot),
m23 = 0,
m30 = 0,
m31 = 0,
m32 = 0,
m33 = 1
};
var matrix = rotMatrix * m_Target.localToWorldMatrix;
m_Target.rotation = matrix.rotation;
}
}
複数の変換行列
複数の変換行列の積は右から順に適用されます。
コードで確認してみます。
private void YXRotation() {
Matrix4x4 matrix = XRotate(-90) * YRotate(90) * m_Target.localToWorldMatrix;
m_Target.rotation = matrix.rotation;
}
private void XYRotation() {
Matrix4x4 matrix = YRotate(90) * XRotate(-90) * m_Target.localToWorldMatrix;
m_Target.rotation = matrix.rotation;
}
private Matrix4x4 XRotate(float degree) {
var rot = Mathf.Deg2Rad * degree;
return new Matrix4x4 {
m00 = 1,
m01 = 0,
m02 = 0,
m03 = 0,
m10 = 0,
m11 = Mathf.Cos(rot),
m12 = -Mathf.Sin(rot),
m13 = 0,
m20 = 0,
m21 = Mathf.Sin(rot),
m22 = Mathf.Cos(rot),
m23 = 0,
m30 = 0,
m31 = 0,
m32 = 0,
m33 = 1
};
}
private Matrix4x4 YRotate(float degree) {
var rot = Mathf.Deg2Rad * degree;
return new Matrix4x4 {
m00 = Mathf.Cos(rot),
m01 = 0,
m02 = Mathf.Sin(rot),
m03 = 0,
m10 = 0,
m11 = 1,
m12 = 0,
m13 = 0,
m20 = -Mathf.Sin(rot),
m21 = 0,
m22 = Mathf.Cos(rot),
m23 = 0,
m30 = 0,
m31 = 0,
m32 = 0,
m33 = 1
};
}
Y→X回転
B=M_{rx} M_{ry} A
X→Y回転
B=M_{ry} M_{rx} A
変換行列が3つ以上になっても右から順に積の演算が行われます。また、変換行列は1つの変換行列としてまとめることもできます。
\begin{aligned}
B & =Mn...M_{3} M_{2} M_{1} A\\
& =MA
\end{aligned}
カメラと行列
Matrix4x4行列の仕組みを辿ってきたところで最後にカメラと行列の組み合わせについてみていきます。Unityのカメラにはワールド空間からカメラ空間に変換する行列を取得または設定するworldToCameraMatrix(ビューマトリックス)プロパティが用意されています。
worldToCameraMatrixはカメラからみてオブジェクトがどのような座標空間で描画するるかを決める変換行列であり、またワールド空間上におけるカメラの位置や視点を司る行列であると考えられます。
そのため、何を基準にした行列を代入するかで結果が変わります。以下のコードで変換行列を右から掛けるか左から掛けるかで見え方の変化を確認することができます。
public class CameraMatrix : MonoBehaviour {
[SerializeField] private Camera m_Camera;
[SerializeField] private bool m_SetRightRotation;
private Matrix4x4 m_Matrix;
private void Start() {
// Y軸回転
m_Matrix = Matrix4x4.TRS(Vector3.zero, Quaternion.Euler(new Vector3(0, 0.1f, 0)), Vector3.one);
}
private void Update() {
if (m_SetRightRotation) {
SetRightRotation();
} else {
SetLeftRotation();
}
}
// 右掛け:変換行列(World空間座標)をCameraWorldに変換=Worldが回転
private void SetRightRotation() {
m_Camera.worldToCameraMatrix = m_Camera.worldToCameraMatrix * m_Matrix;
}
// 左掛け:CameraWorld空間を変換行列で変換=Cameraが回転
private void SetLeftRotation() {
m_Camera.worldToCameraMatrix = m_Matrix * m_Camera.worldToCameraMatrix;
}
}
右掛け
M'_{worldToCam} =\ M_{worldToCam} R_{yWorld}
左掛け
M'_{worldToCam} =\ R_{yWorld} M_{worldToCam}
このように結果が変わることから、以下の用途で使い分けるのがよさそうです。
右掛け:カメラの描画空間に変更を加えたいとき
左掛け:カメラの向きや位置の変更を加えたいとき
worldToCameraMatrixを使用する場合の注意点
worldToCameraMatrixに行列を設定すると、Transformに基づいた描画を行わなくなるため再度Transformによる更新を行いたい場合はResetWorldToCameraMatrixメソッドを呼び出す必要があります。
おわりに
この記事を書いた動機はカメラのworldToCameraMatrixを使いこなせるように調べた内容をまとめたかったからでした。記事を書き終わってみると今までおぼろげだった行列の理解が少しだけ進んだように感じます。
冒頭で触れたようにUnityでオブジェクトの座標変換を行う場合は、Transformやクォータニオンを操作することがパフォーマンス的にも一般的です。しかしカメラの描画空間の変換処理はどうしても行列の知識が必要になってくるため、この記事が少しでも行列の理解のお役に立てれば幸いです。🌱
参考リンク
https://github.com/Unity-Technologies/UnityCsReference/blob/master/Runtime/Export/Math/Matrix4x4.cs
https://edom18.hateblo.jp/entry/2019/01/04/153205
http://hideki-todo.com/cgu/lectures/cg2015/04_basic1/04_basic1.pdf
https://light11.hatenadiary.com/entry/2019/01/07/213408
https://imagingsolution.net/imaging/affine-transformation/
https://docs.unity3d.com/ScriptReference/Matrix4x4.html
使用した3Dモデルライセンス
© Unity Technologies Japan/UCL