任意のデータをより効率的に検索する実用的な方法として、
ハッシュテーブルを用いた実装が挙げられます。
ハッシュテーブルの長さには任意の値をとることが出来ますが、
一般的には「素数」を用いるのが良いと言われています。
その理由について厳密な証明をするためには、離散数学に関する知見が必要ですが、
ここでは簡単に、ハッシュテーブルの各スロットに線形リストを持たせた
「チェイン法」を例に、図を用いて説明していきます。
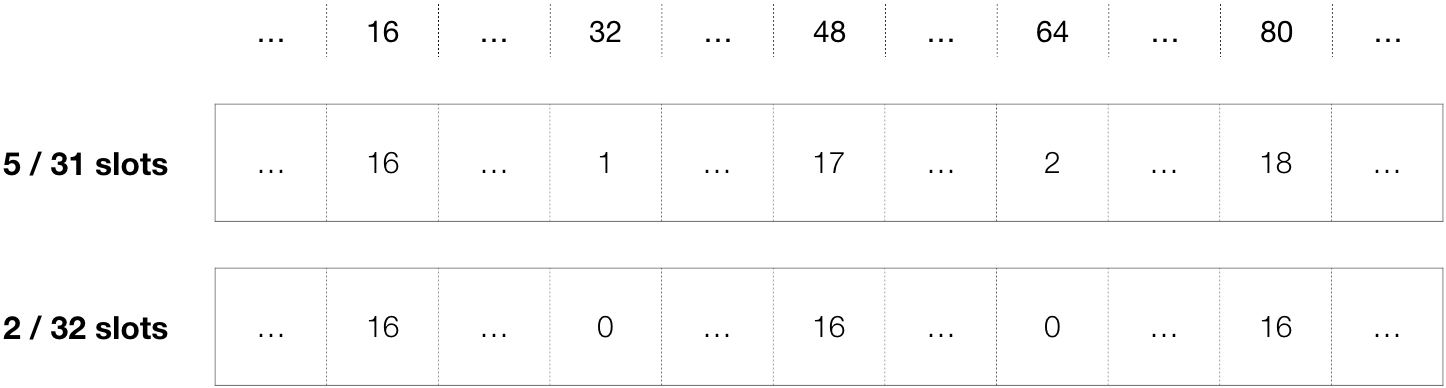
上図のように、ハッシュテーブルの長さが31スロットのものと32スロットのものを考えます。
ハッシュ関数への入力するキーを「1 ~ 100」までの連番としたとき、
それらの中でも、例えば「16, 32, 48, 64, 80」に注目してみましょう。
ハッシュテーブルの長さに「31」という「素数」を指定した場合は、
先ほどピックアップしたキーに対する剰余(ハッシュ値)が「16, 1, 17, 2, 18」となり、
これらの番号のスロットへ、データが挿入されることになります。
このとき、スロットの使用率は$\frac{5}{31}$です。
しかしながら、ハッシュテーブルの長さに「32」という「2のべき乗」を指定した場合、
各キーに対する剰余(ハッシュ値)は「16, 0, 16, 0, 16」となり、
これらの番号を持つスロットへ、データが挿入されます。
そして、スロットの使用率は$\frac{2}{32}$です。
後者は、明らかにハッシュ値が重複しており、
結果的に、特定のスロットに偏ってデータが挿入されています。
このような事例を回避するために、ハッシュテーブルの長さには「素数」を用いると良いのですが、
それが適当であるのは、今回のように整数や文字列など、全体として連番に近い値をキーとして扱う場合のみです。
逆にそうでない場合は、あえて「2のべき乗」を用いると良いときもあります。
いずれにせよ、入力するデータの性質に応じて、適切なハッシュテーブルの長さを用いていきましょう。
当記事が、どなたかの一助となれば幸いです。