はじめに
『統計にそんなに詳しくないけど、機械学習とかのモデルを自分で実装してみたい!』
ってことよくありますよね?
『そんなこと全くないわー(#^ω^)』って思った人も素直になってください。
絶対に一度は思ったことがあるはずです。
とくにPythonでロジスティック回帰を実装したいと思ったことがある人は多いと思います。
多いはずです。
ここでは、統計の知識をヌルくと説明しつつPythonで実際に動くLogistic回帰モデルを実装します。
統計に詳しくない方でも無理なく出来るよう、統計の説明➔実装 を1ステップづつ進められるようにしました。
なんでかんで、統計モデルとか機械学習も自分で実装しながら覚えると効率がよかったりします。
この記事の対象読者
基本的にはデータサイエンスに多少興味ある方向けです。
- ロジスティック回帰って聞いたことあるけど、よくわからん
- 上司がロジスティック回帰でクラシファイしろとうるさい
- 統計は詳しくないけど、実装しながらなら学べる気がする
- 最低限の知識はあるけど、どうやって動いてるのか知りたい
- ロジスティック回帰ならもちろん使ったことあるよ?パッケージで一発じゃん。
じ、自前実装はしたこと無いけど/// な、なんか文句あんの?
あわせて読みたい
データサイエンティストに興味があるならまずこの辺りを見ておきな、って文献・動画のまとめ
http://qiita.com/hik0107/items/ef5e044d2f47940ba712
そろそろデータサイエンティストの定義とスキルセットについて本気で考えてみる
http://qiita.com/hik0107/items/f9bf14a7575d5c885a16
準備
次の設定をしておいてください。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import optimize
plt.style.use('ggplot')
あとこちらの記事でロジスティック回帰の概要だけ勉強するとより良いかも
(なんとなく雰囲気がわかれば大丈夫です。)
http://gihyo.jp/dev/serial/01/machine-learning/0018
実装
データを生成する
今回は簡単のために要素2つと、2値の分類だけを持つデータを作ります。
$x,y$ が要素、$c=[1,0]$の2値分類とします。
この組み合わせを$N点$生成してPandas Data Frameに格納する関数を作りましょう。
$ obs_i = (x_i, y_i, c_i) $ ただし $i = 1,2,3 ....N$
$x_i, y_i$は numpyのモジュール "np.random" で簡単に作ることが出来ます。
$c$に関しては、ある分離線を人為的に定義し、その分離線のどちら側にいるかで割り振ることにします。
仮に分離線を $ 5x + 3 y = 1 $ としましょう。
つまり、 $g(x,y) = 5x_i + 3y_i -1$ として、 $g(x, y) >0 ⇛ c=1$ 、$g(x, y) < 0 ⇛ c=0$ となるようにします。
def make_data(N, draw_plot=True, is_confused=False, confuse_bin=50):
'''N個のデータセットを生成する関数
データをわざと複雑にするための機能 is_confusedを実装する
'''
np.random.seed(1) # シードを固定して、乱数が毎回同じ出力になるようにする
feature = np.random.randn(N, 2)
df = pd.DataFrame(feature, columns=['x', 'y'])
# 2値分類の付与:人為的な分離線の上下どちらに居るかで機械的に判定
df['c'] = df.apply(lambda row : 1 if (5*row.x + 3*row.y - 1)>0 else 0, axis=1)
# 撹乱:データを少し複雑にするための操作
if is_confused:
def get_model_confused(data):
c = 1 if (data.name % confuse_bin) == 0 else data.c
return c
df['c'] = df.apply(get_model_confused, axis=1)
# 可視化:どんな感じのデータになったか可視化するモジュール
# c = df.c つまり2値の0と1で色を分けて表示するようにしてある
if draw_plot:
plt.scatter(x=df.x, y=df.y, c=df.c, alpha=0.6)
plt.xlim([df.x.min() -0.1, df.x.max() +0.1])
plt.ylim([df.y.min() -0.1, df.y.max() +0.1])
return df
この関数の出力を見てみましょう
df = make_data(1000)
df.head(5)
Out[24]:
x y c
0 1.624345 -0.611756 1
1 -0.528172 -1.072969 0
2 0.865408 -2.301539 0
3 1.744812 -0.761207 1
4 0.319039 -0.249370 0
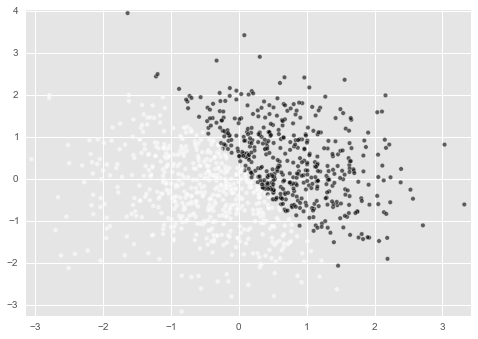
ある線を堺にc=1とc=0分かれているのがわかると思います。
ここが上記で定義した $ 5x + 3 y = 1 $の線になっています。
これから実装するLogistic回帰モデルがこの分離線を予測することができれば成功です。
なお、今回はこのデータ生成関数に少しおまけを付けました。
df_data = make_data(1000, is_confused=True, confuse_bin=10)
このように引数を指定すると、白点の領域に黒点を紛れ込ませることが出来ます。
紛れ込む量はconfuse_binが小さくなるほど大きくなるように設定してあります。
これがどのような意味を持つかは後ほど(もうわかってる方もいると思いますが)
確率値を計算する
ロジスティック回帰の冥利は、『c=1と考えてよいかどうかの可能性の高さ』を $ 0 ≦ p ≦1$ の確率値として出力することで、各データがどの程度の確からしさで $[1, 0]$ の2値いずれに分類されるかを明らかに出来る点にあります。
なので、次はこの確率値pの計算を実装します。これは理論的な側面を横に置けば簡単です。
まず結論のコードから見てしまいましょう。
def sigmoid(z):
return 1.0 / (1 + np.exp(-z))
def get_prob(x, y, weight_vector):
'''特徴量と重み係数ベクトルを与えると、確率p(c=1 | x,y)を返す関数
'''
feature_vector = np.array([x, y, 1])
z = np.inner(feature_vector, weight_vector)
return sigmoid(z)
以上です。すごく簡単ですよね?
少しだけ補足します。(理論面に興味がある方はググれば大量に情報はあります。)
ある観測点が $c=1$ に分類される確率 $p(c=1 | x )$ は次のように記述されます。
$ p = \frac{1}{1 + exp(-f)}$ ただし $ f = ∑ w_iφ(x_i) $
今回で言うと、 $ f = w_1x + w_2y + w_3$ です。
ここで $w_1,w_2,w_3$は 重み と呼ばれるパラメータを指します。
要は、x-y軸のグラフ上でいうところの、線の傾きとか切片を指しています。
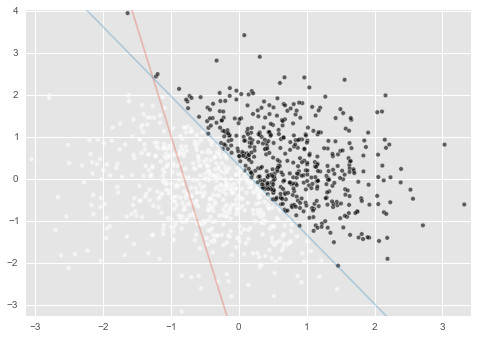
この図で、赤の線は c=1とc=0(黒と白)を上手く分離してない感が凄いですよね。
これは$w_1,w_2,w_3$といった各重みが、このデータの分類をおこなうためのモデルとして間違っているからです。
この赤い線じゃ嫌なので、青い線みたくc=1とc=0(黒と白)を上手く分離できてるっぽい重みを探すというのが、『ロジスティック回帰のモデルを作る』ということに相当します。
うーん、簡単そう。
じゃあ一番いい"重み"を探そうぜ
ここから少しやっつけで行きます。みんな大好き最尤推定です。
尤度(ゆーど)は重みベクトル $w$ をパラメータとして、次のように記述できる
$ E(w) = ∑- log(L_i) $
ただし、$c_i= [1 , 0]$を正解として持つある観測点の尤度 $L_i$は次のように定義される。上述のように $p_i$は$w$の関数となっている。
$L_i = c_i log (p_i) +(1-c_i) log(1-p_i) $
なんだか難しそうなことを言っていますが、そんなに難しくありません。
このように考えてみましょう。
3つの点があり、この点の分類値は$(c_1, c_2, c_3) =(1,1,0)$ が正解だったとします。
黒黒白 ですね。
さて、ここにロジスティック回帰で作った2つの予測モデルがあったとしましょう。
それぞれのモデルは、この3つの点が1(黒)である確率を次のように予想しました。
どちらが良いモデルでしょうか?
$M_1 : (p_1,p_2,p_3) = (0.8, 0.6, 0.2)$
$M_2 : (p_1,p_2,p_3) = (0.9, 0.1, 0.1)$
直感的には、
①各点(1~3)の予測がどの程度あたっているかを考え
②その3つの合算を考えれば
全体として、どの程度よい良い予測かということが言えそうな気がしますね。
統計的には次のように考えます。例えば$M_1$の例では
$p_1$は $正解:c=1$に対して、0.8と予測しているので、0.8ポイント
$p_2$は $正解:c=1$に対して、0.6と予測しているので、0.6ポイント
$p_3$は $正解:c=0$に対して、0.2と予測しているので、(1.0-0.2)=0.8ポイント
合計の得点は 0.8, 0.6, 0.8を 掛けあわせたもの とする。
※ $p_3$は0.2ポイントではないことに注意
このやり方で、$M_1$と$M_2$の得点を比べれば『どちらがいいモデルかが比較できる』というやり方です。
実際にはN点のデータで予測する場合は$p_1, p_2 ...p_N$の予測の掛け合わせになります。
また、モデルは2個ではなく無数に考えられる可能性の中から一番良い物を探します。
おそらくこの点で疑問はたくさんあると思います。
詳しくは『最尤推定 さいゆーすいてー 』でググって下さい
Q. なんで得点を掛け合わせるんだよ
A. 確率だからです
Q. 上の式で出てきた$log$は何なんだ?
A. $log$は掛け算を足し算に変換できるなど、利点があります。
Q. 勝手に$log$とかしたら式の意味が変わるじゃねーか。あとマイナスは何だよ
A. $log$ を取った値の最大化は元の値の最大化と一致するんです
A. 最大化問題を最小化問題に置き換えています > マイナス
Q. どうやって無数に考えられる可能性から一番いいものを探すんだ?
A. 次の章で扱いますが、あまり詳細に説明していません。
重みを探してくれ:最尤推定
まず、最適化したい尤度を実装します。
再掲ですが、あるモデル(= ある重み $w_1,w_2,w_3$)の尤度は下記のように定式化されるので、それをコード化しているだけです。
$ E(w) = ∑- log(L_i) $
ただし、$L_i = c_i log (p_i) +(1-c_i) log(1-p_i) $
def define_likelihood(weight_vector, *args):
'''dfのデータセット分をなめていき、対数尤度の和を定義する関数
この関数をOptimizerに喰わせてパラメータの最尤推定を行う
'''
likelihood = 0
df_data = args[0]
for x, y, c in zip(df_data.x, df_data.y, df_data.c):
prob = get_prob(x, y, weight_vector)
i_likelihood = np.log(prob) if c==1 else np.log(1.0-prob)
likelihood = likelihood - i_likelihood
return likelihood
そして上記コードで定義した尤度が一番いい感じになるような重み$w_1,w_2,w_3$を探します。
ここは自前実装は避け、scipy.optimizeという、関数の最小化解などを探すためのパッケージに任せます。
def estimate_weight(df_data, initial_param):
'''学習用のデータとパラメータの初期値を受け取って、
最尤推定の結果の最適パラメータを返す関数
'''
parameter = optimize.minimize(define_likelihood,
initial_param, #適当に重みの組み合わせの初期値を与える
args=(df_data),
method='Nelder-Mead')
return parameter.x
ここで行ったような、
- 分類の結果を要素($x$とか$y$とか)x その重み $w_1,w_2,w_3$ で表現
- 尤度を重みの関数として表現
- 尤度を最適化するような重みの組み合わせを探す
という流れは統計モデルや機械学習の世界だと非常によく出てきます。
是非覚えておいて損はないと思います。
では実装した関数を実行して、最適な重みを見つけてみましょう。
まず適当に重みの初期値を定義します。これは完全に適当です。
※最適化の問題によっては初期値の値によって結果が変わることがありますが、ここでは適当で大丈夫です。
weight_vector = np.random.rand(3)
weight_vector
Out[26]:
array([ 0.91726016, 0.15073966, 0.24376398])
# データを作成するして、プロットする
df_data = make_data(1000)
# 適当な初期値の重みを設定して、分離面を描画してみる
weight_vector = np.random.rand(3)
draw_split_line(weight_vector)
ここでは、分離面を描画するために次のような関数を作っておきました。
def draw_split_line(weight_vector):
'''分離線を描画する関数
'''
a,b,c = weight_vector
x = np.array(range(-10,10,1))
y = (a * x + c)/-b
plt.plot(x,y, alpha=0.3)
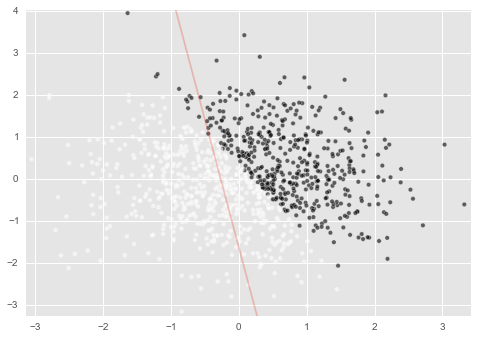
結果はこんな感じです。適当に引いたので当然的外れですね。
では、白と黒を上手いこと分けるように、いい感じの重みを見つけましょう。
weight_vector = estimate_weight(df_data, weight_vector) #最尤推定の実行
weight_vector
Out[30]:
array([ 10013.66435446, 6084.79071201, -2011.60925704])
最適な重みが発見されました。
ここで、今回定義した分離面が$ 5x + 3 y = 1 $ であったことを思い出してください。
重み $(w_1,w_2,w_3)$ が $(5:3:-1)$ に近い関係になっているのがわかるでしょうか?
draw_split_line()で線を引いてやると下図のようになります。
溢れでる上手いこといってる感
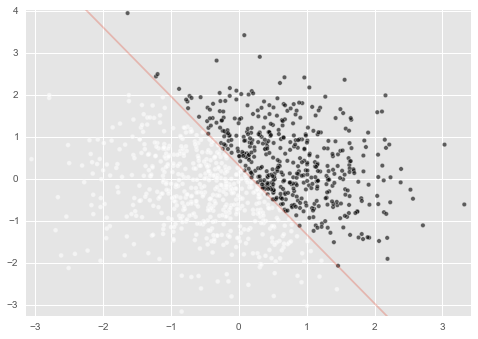
c=1 の 確率pはどうなった
あと一息です。
とりあえず次のような関数を実装します。
def validate_prediction(df_data, weight_vector):
a, b, c = weight_vector
df_data['pred'] = df_data.apply(lambda row : 1 if (a*row.x + b*row.y + c) >0 else 0, axis=1)
df_data['p'] = df_data.apply(lambda row : sigmoid(a*row.x + b*row.y + c), axis=1)
return df_data
**"pred"**はP=0.5以上になった点をc=1と予測した時の予測値
**"p"**はc=1である確率の予測値です。
df_pred = validate_prediction(df_data, weight_vector)
df_pred.head(10)
Out[33]:
x y c pred p
0 1.624345 -0.611756 1 1 1.000000e+00
1 -0.528172 -1.072969 0 0 0.000000e+00
2 0.865408 -2.301539 0 0 0.000000e+00
3 1.744812 -0.761207 1 1 1.000000e+00
4 0.319039 -0.249370 0 0 7.043082e-146
5 1.462108 -2.060141 1 1 1.000000e+00
6 -0.322417 -0.384054 0 0 0.000000e+00
7 1.133769 -1.099891 1 1 1.000000e+00
8 -0.172428 -0.877858 0 0 0.000000e+00
9 0.042214 0.582815 1 1 1.000000e+00
実際のcの値とpredの値が一致しているので、予測が成功というところでしょうか。
気になる方は1000データ全て確認してみてください。
また、確率値pが求められています。
単純に1,0いずれかの答えを吐くのでなく、この$p$を得ることが出来るのがロジスティック回帰の特性です。
pがどんな感じになっているか見てみましょう。
def draw_prob(df_data):
df = validate_prediction(df_data, weight_vector)
plt.scatter(df_data.x, df_data.y, c=df_data.p, cmap='Blues', alpha=0.6)
plt.xlim([df_data.x.min() -0.1, df.x.max() +0.1])
plt.ylim([df_data.y.min() -0.1, df.y.max() +0.1])
plt.colorbar()
plt.title('plot colored by probability', size=16)
こんな感じで$p$を可視化する関数を適当に作りました。
せっかくなのでここまで作った関数を使って、全体の流れを通しで実行します。
plt.figure(figsize=(16, 4))
plt.subplot(1,2,1) #2つの図を並べて表示する準備
# データを作成するして、プロットする
df_data = make_data(1000)
# 適当な初期値の重みを設定して、分離面を描画してみる
weight_vector = np.random.rand(3)
draw_split_line(weight_vector)
# 最尤推定で重みを推定し、分離面を描画してみる
weight_vector = estimate_weight(df_data, weight_vector)
draw_split_line(weight_vector)
plt.title('plot with split line before/after optimization', size=16)
# pの可視化
plt.subplot(1,2,2)
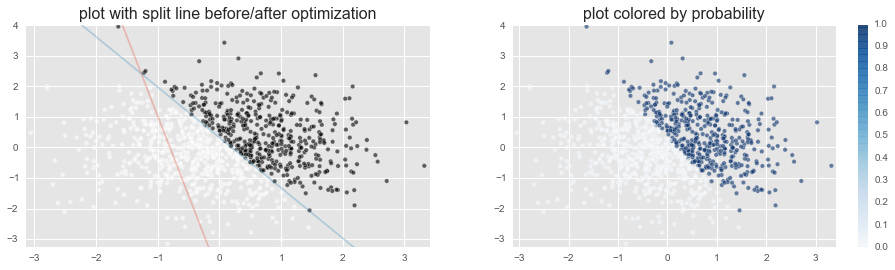
draw_prob(df_data)
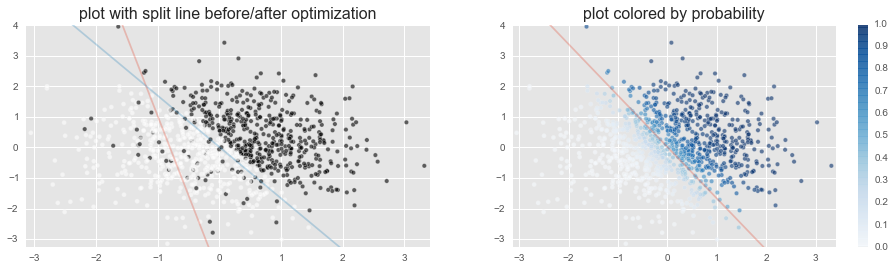
分離面を堺に、c=1である確率p(右図の青さの度合い)がくっきり分かれているのがわかります。
これはデータ自体が、分離面の上下で c= 1 or 0 がはっきり別れたようなデータだったからです。
言葉通り、白黒はっきり というやつです。
実際のデータでは、こんなにキレイにcの値が別れることはないでしょう。
もう少し複雑なデータでやってみる
そこで、もう少し複雑性の高いデータでやってみます。
上記のデータを思いだして下さい。
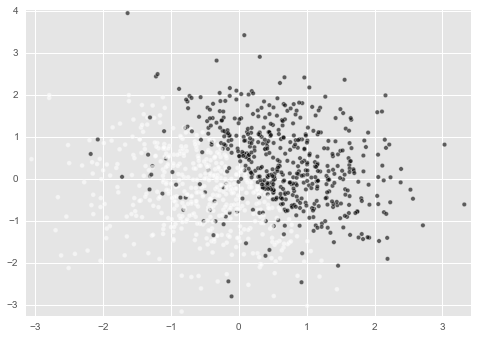
現実はこんな感じに同じ領域に居るデータでもc=1だったりc=0だったりするのが普通です。
この場合どうなるでしょうか?
plt.figure(figsize=(16, 4))
plt.subplot(1,2,1)
# データを作成するして、プロットする(ここだけさっきと違う)
df_data = make_data(1000,is_confused=True, confuse_bin=10)
# 適当な初期値の重みを設定して、分離面を描画してみる
weight_vector = np.random.rand(3)
draw_split_line(weight_vector)
# 最尤推定で重みを推定し、分離面を描画してみる
weight_vector = estimate_weight(df_data, weight_vector)
draw_split_line(weight_vector)
plt.title('plot with split line before/after optimization', size=16)
plt.subplot(1,2,2)
draw_prob(df_data)
# draw_split_line(weight_vector)
だいぶ結果が変わりました。
左図では、分離面の位置が少し白のカタマリ群の方に寄り、右図では分離面付近の色がモヤッとしています。
これは、 データが先程より白黒はっきりしたものでないので、モデルも白黒はっきりできないということです。
この青さが◯◯以上の時にc=1を判断する(例えば0.6以上など)、ロジスティック回帰の考え方です。
まとめ
- ロジスティック回帰をPythonで自前実装しました
- ロジスティック回帰の理論についてなんとなく学びました
- 機械学習の分類モデルが自分で作れそうという自信がつきました