RDBのインデックスについて理解を深めようとすると必ず行き当たるのがB木ですが、なんとなくわかっているけどきちんと理解できていなかったので学んだことを10分程度で理解できるよう具体的なケースでまとめました。
B木(B-tree)
特徴
B木は木構造の一種で、全レコードを順番に探索（シーケンシャルスキャン） O(N) するよりも少ない計算量 O(logN) で目的のデータまで到達できるアルゴリズムです。
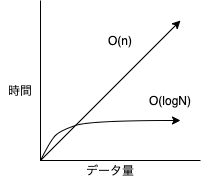
計算量のイメージとしては上図のようになり、データ量が増えても計算時間がほとんど変わらないのが一番の特徴です。
以下の特徴があるため、バランス良くデータが配置され安定したパフォーマンスを発揮できます。（値によって遅いときと速いときの差が出にくい）
- 葉ノード以外はすべて2つ以上の子ノードを持つ
- M個のキーを持つ節点はM＋1個の子ノードを持つ
- 葉ノードはすべて同じレベルになる
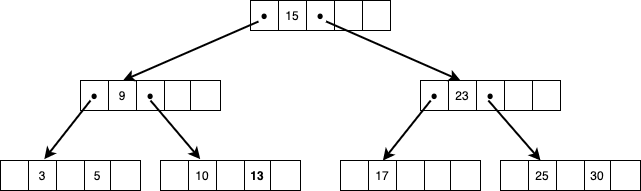
- 子ノードには小さい値と大きい値が入り、親ノードには中間値が入る構造になる
論理イメージとしては上図のようになり、左に小さい値、右に大きい値のノードをぶら下げる構造となっています。
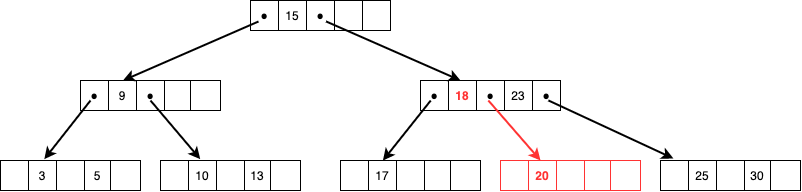
値の検索
- ルートノードからポインタをたどる
- 葉ノードの前のノードで見つかる場合もある
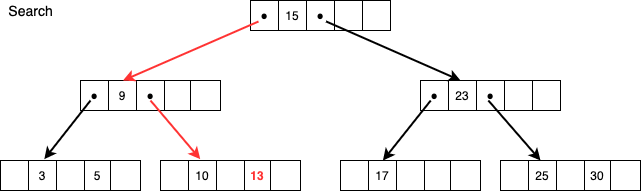
上図のように13という値を検索する場合、ルートノードが15なので左のポインタをたどり、9よりも大きいので右のポインタをたどり、目的の13が含まれるノードに辿り着きます。
値の挿入
- ノードに空きがある場合はそのまま追加する
- オーバーフローする場合は中間値を親ノードに追加して新しいノードを作成する
- オーバーフローはさらに親ノードに波及する場合があり、最終的にルートノードまで実施する
ノードに空きがあるケース
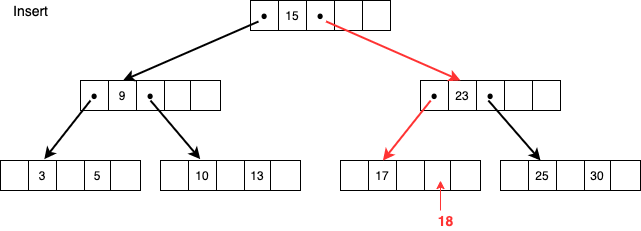
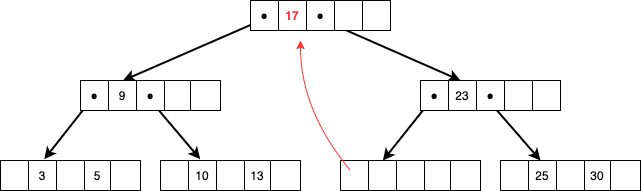
上図は18を挿入する例で、検索時と同様にルートノードからたどって17が含まれているノードに空きがあるのでそのまま挿入してこのケースは終了となります。
ノードに空きがなく、オーバーフローするケース
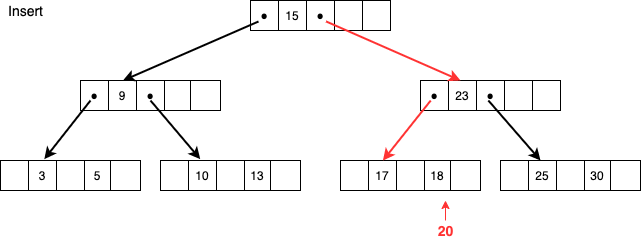
この状態から次に20を追加しようとした場合、同様に17が含まれているノードに追加するのが適当なのですが、空きがないため新しいノードを作る必要があります。
ルールに則り17,18,20の中間値18を親ノードに追加して17,20を子ノードとして新たにひとつ作成しポインターを親ノードに追加して終了です。
親ノードにも空きがないケース
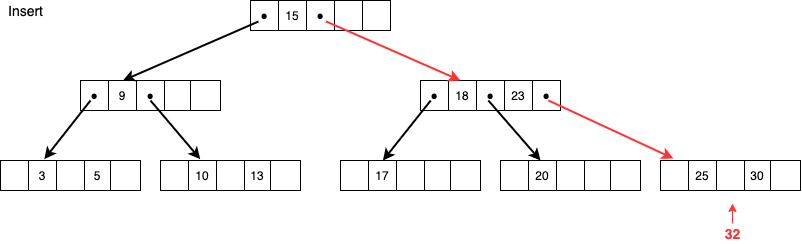
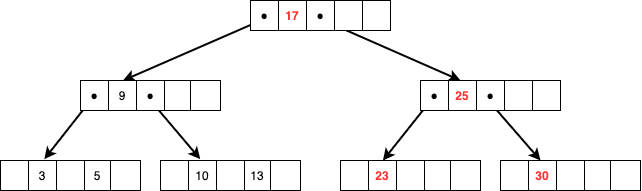
この状態からさらに32という値を追加する場合、同様に25,30,32から中間値である30を親ノードに追加して32を持つ子ノードを追加しようとします。
しかし親ノードに空きがないため、18,23,30で同様に分割します。
中間値である23をルートノードに追加し、新たに30の値を持つノードを追加して無事終了です。
値の削除
削除は大きく2つのケースがあり、削除対象が「葉ノードにある場合」と「葉ノード以外の場合」があります。
葉ノードの場合
- ノードに2つ以上のレコードがあるならそのまま削除
- 削除する値があるノードに値が1つしかないならアンダーフロー処理する
- 同じ親ノードにぶら下がっている別ノードから値を持ってきて、親ノードに中間値を置き換える
- 別ノードにもってこれる値がない場合、中間値を親ノードから持ってきて、親ノードからその中間値を削除する
ノードに2つ以上のレコードがあるケース
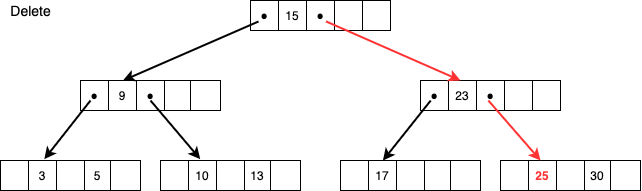
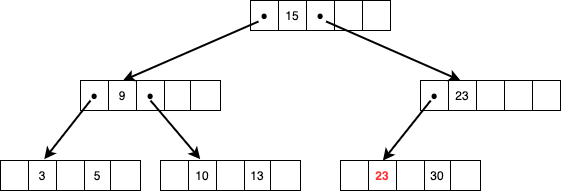
上図のように25を削除する場合、同じノードに30という値があるため25を削除後も1つ以上の値があるという条件が満たされるためこれ以上は特になく終了です。
ノードに値が1つしかないケース
さらに17を削除しようとするとそのノードに値が1つもない状態となってしまうため、アンダーフロー処理を行います。
同じ親ノードにぶら下がっているノードに2つ以上の値をもっているものがあればそこからとって中間値を親ノードに置き換える処理をすればいいのですが、今回は301つしか持っていないノードしかないため、親ノードにある23をもってきて30のノードにマージします。
親ノードの23は削除するため今度はさらに親ノードであるルートノードから15を持ってきます。
ルートノードにあった15を削除したためルートノードが1段すくなくなり終了です。
葉ノード以外の場合
- 右側の葉ノードにある、削除する値とその次に大きな値を置き換える
- その際にアンダーフローが発生する場合は葉ノードでアンダーフローが発生した際の処理を行う
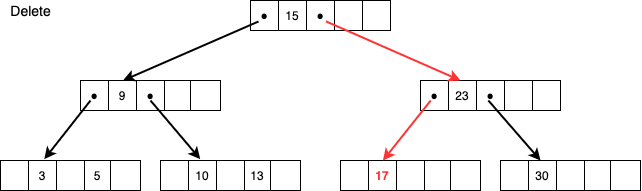
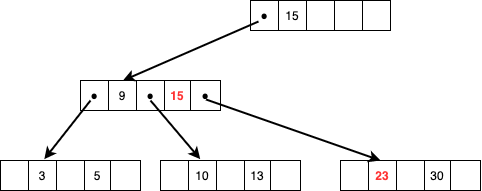
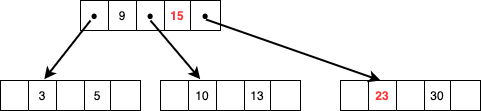
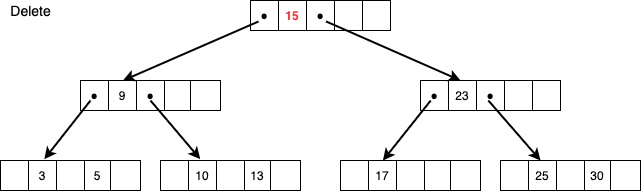
上図のようにルートノードの15を削除するケースを考えます。
ルールに則り、右側のポインタにぶら下がっている一番小さい値17を持ってきて15があったところに格納します。
元々17があったノードに値がなくなったためアンダーフロー処理を行い、23,25,30のうちの中間値である25を親ノードにして23,25を子ノードに格納して終了です。
B+木(B+ -tree)
B木の発展版で、MySQLやPostgreSQL、Oracle等メジャーなRDBで広く使われているアルゴリズムです。
検索、挿入、削除いずれも基本的にはB木と同じロジックとなるためここではB木の違いと検索の説明までに留めます。
B木との違い
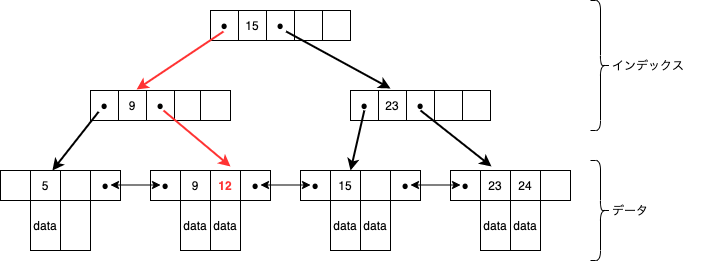
B木で構成されたインデックス部と、データを葉ノードに格納した構造となっています。
このためB+木では比較的大きなデータも扱えるようになり、ページあたりのポインタも増やしやすくなるためB木と比較して検索効率も高いようです。
また、葉ノードにシーケンシャルなデータが格納されているため範囲検索が得意なことも特徴です。
値の検索
B木と同様にポインターをたどりますが、図にあるようにデータは一番下の葉ノードに存在します。
範囲検索
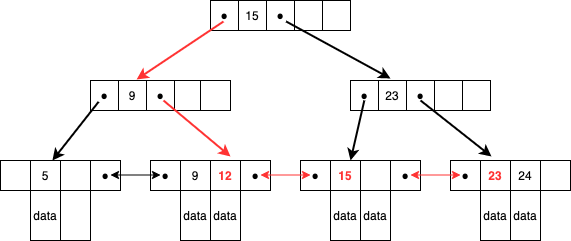
例として12〜23の範囲検索を行った場合、まず小さい方の値である12を検索し、そこから右のポインタをたどって23で終了します。
葉ノードがポインターで繋がっているためB木よりも効率的に範囲検索が行えることがわかります。
おわりに
メジャーなRDBに広く使われているB木ですが、基礎を固めておくと様々なケースで応用が効き理解が深まりそうですね