information
本記事は2025年4月26日(土)開催のTokyoRにて発表予定の初心者セッション資料その2です。
TokyoR発表資料
その1 「"The R Foundation for Statistical Computing"を実感する」
その3 「Rの統計関連(dpqr)関数の書き方」
その4 「誕生日のパラドックスをRの関数で求める方法」
Rを利用し始めると、dnorm(), pnorm(), qnorm(), rnorm()は早晩見ることになるかと思います。ただ、rnorm()以外は慣れないと、どのときにどれを使えばよいかわからなくなってしまうことも多いかと思います。そこで、d,p,q,rが何の意でどのように使用するのか、まとめてみます。
d*,p*,q*,r*の意味を改めて知る
そもそもRには単体の関数として、d(), p(), qn(), r()があります。
Four generic functions that take a distribution object (e.g. Bern) and return the density, cumulative probability, quantile, and random generator functions, respectively.
(日本語訳)
分布オブジェクト(ベルヌーイ分布など)を受け取り、それぞれ密度関数、累積確率関数、分位関数、ランダム生成関数を返す4つの汎用関数。
実際に上記リンクのExamplesを実行してみると理解が進むと思います。
1. d*: 確率密度関数 (Probability Density Function)
指定した値におけるの確率密度を計算します。グラフで言うと「高さ」を返します。
- 引数:確率密度を計算したい$x$(ベクトルでも可)
- 戻り値:$x$における確率密度(グラフの高さ、$y$の値)
2. p*: 累積分布関数 (Cumulative Distribution Function, CDF)
指定した値以下の確率(累積確率)を計算します。グラフで言うと、左側($x$の最小値)から$x(q)$までの面積を返します。
- 引数:累積確率を計算したい$q$(ベクトルでも可)
- 戻り値:$x \leq q$の確率(グラフの面積、累積確率$p \mid 0 \leq p \leq 1$)
3. q*: 分位点関数 (Quantile Function)
指定した確率に対応する分位点(値)を計算します。p*()の逆関数で、累積確率から$x$を求めます。グラフで言うと、累積面積からその地点の$x$の値をかえします。
- 引数:求めたい:$x \leq q$の確率(グラフの面積、累積確率$p \mid 0 \leq p \leq 1$)
- 戻り値:指定した確率に対応する $x$ の値
4. r*: 乱数生成関数 (Random Number Generation)
正規分布に従う乱数を生成します。シミュレーションやデータ生成に使用されます。
- 引数:生成する乱数の個数$n$
- 戻り値:乱数のベクトル
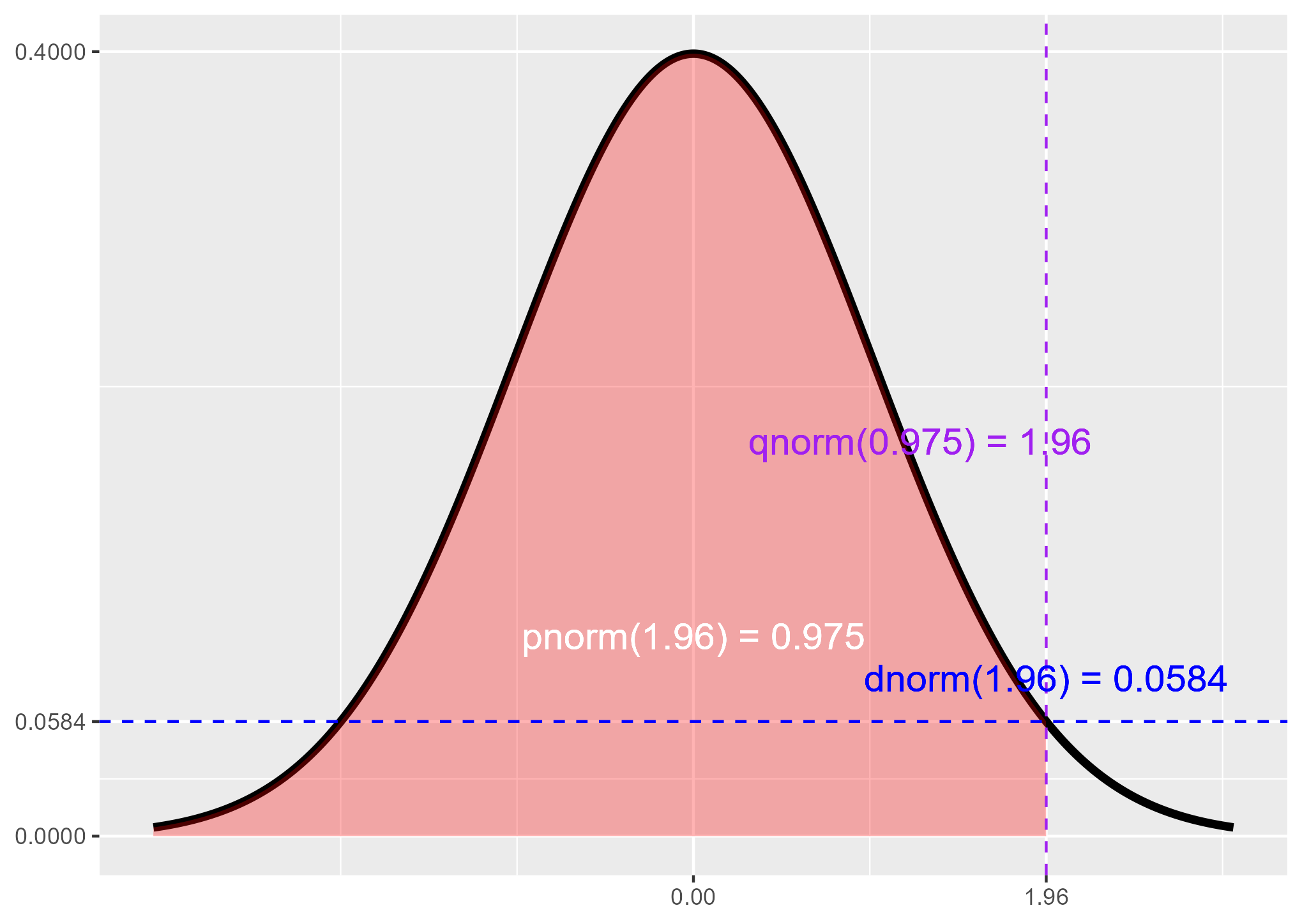
標準正規分布グラフでdnorm() pnorm() qnorm()を理解する
> dnorm(1.96)
[1] 0.05844094
> qnorm(0.975)
[1] 1.959964
> pnorm(1.96)
[1] 0.9750021
と記載されてもなかなかイメージができないと思いますので、ggplot()で作成した標準正規分布グラフを貼っておきます。
q=1.96の時のグラフとRの関数
乱数を生成するrnorm() runif()
rnorm()は正規分布の中からn個のサンプルを抽出してくれます。どの値も均等の確率(一様分布)の中からn個のサンプルを抽出したい場合はrunif()を使います。私はrunif()をrun + if かと思っていましたが、r + unifだったんですね笑。
また、r*ではありませんが、整数値の乱数生成にはsample()もよく使われます。
> rnorm(5)
[1] -1.92688778 -0.47249826 0.04947606 0.38249702 -1.94726251
> # runifのデフォルトはmin = 0, max = 1
+ runif(5)
[1] 0.5810854 0.8058259 0.2944058 0.2467517 0.6735231
> # 整数の乱数生成の場合はsample()が便利。
+ sample(1:100, size = 5, replace = TRUE)
[1] 84 45 20 14 26
base Rで使える統計関連(dpqr)関数チートシート
以下にRの基本パッケージ(stats)で使える関数一覧をまとめました。
| 日本語区分名 | 英語名 | d* | p* | q* | r* |
|---|---|---|---|---|---|
| ベータ分布 | beta | dbeta |
pbeta |
qbeta |
rbeta |
| 二項分布 | binom | dbinom |
pbinom |
qbinom |
rbinom |
| 誕生日パラドックス | birthday | pbirthday |
qbirthday |
||
| コーシー分布 | cauchy | dcauchy |
pcauchy |
qcauchy |
rcauchy |
| カイ二乗分布 | chisq | dchisq |
pchisq |
qchisq |
rchisq |
| 指数分布 | exp | dexp |
pexp |
qexp |
rexp |
| F分布 | f | df |
pf |
qf |
rf |
| ガンマ分布 | gamma | dgamma |
pgamma |
qgamma |
rgamma |
| 幾何分布 | geom | dgeom |
pgeom |
qgeom |
rgeom |
| 超幾何分布 | hyper | dhyper |
phyper |
qhyper |
rhyper |
| 対数正規分布 | lnorm | dlnorm |
plnorm |
qlnorm |
rlnorm |
| ロジスティック分布 | logis | dlogis |
plogis |
qlogis |
rlogis |
| 多項分布 | multinom | dmultinom |
rmultinom |
||
| 負の二項分布 | nbinom | dnbinom |
pnbinom |
qnbinom |
rnbinom |
| 正規分布 | norm | dnorm |
pnorm |
qnorm |
rnorm |
| ポアソン分布 | pois | dpois |
ppois |
qpois |
rpois |
| 符号順位分布 | signrank | dsignrank |
psignrank |
qsignrank |
rsignrank |
| t分布 | t | dt |
pt |
qt |
rt |
| テューキー分布 | tukey | ptukey |
qtukey |
||
| 一様分布 | unif | dunif |
punif |
qunif |
runif |
| 離散一様分布 | unifdisc | dunifdisc |
punifdisc |
qunifdisc |
runifdisc |
| ワイブル分布 | weibull | dweibull |
pweibull |
qweibull |
rweibull |
| ウィルコクソン分布 | wilcox | dwilcox |
pwilcox |
qwilcox |
rwilcox |
もちろんライブラリインストールで更なる関数も
base Rでこれだけの関数が用意されているのがRの美点ですが、ライブラリをインストールすることで他にもいろいろな関数が使えます。特にlibrary(extraDistr)は様々な関数を用意してくれています。統計に精通している方はextraDistrマニュアルは一読の価値ありです。
information
TokyoRの発表はその3に続きます。
TokyoR発表資料
その1 「"The R Foundation for Statistical Computing"を実感する」
その3 「Rの統計関連(dpqr)関数の書き方」
その4 「誕生日のパラドックスをRの関数で求める方法」