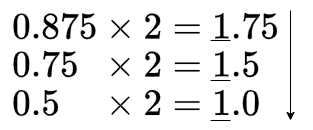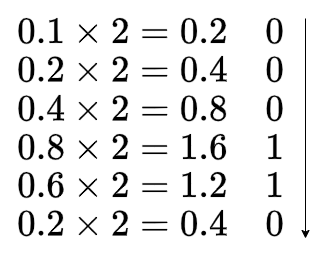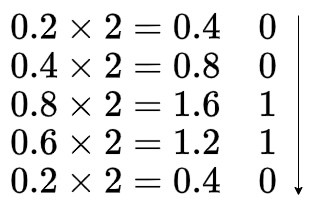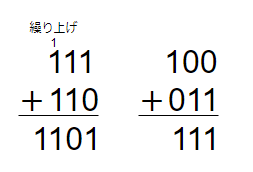この記事はNuco Advent Calendar 2023の4日目の記事です。
弊社では、経験の有無を問わず、社員やインターン生の採用を行っています。
興味のある方はこちらをご覧ください。
はじめに
後輩に 「なぜ0.1+0.2≠0.3になるんですか？」 と聞かれて答えられますか？
コンピュータの計算では「0.1+0.2」は「0.3」になりません。
これを理解していないと予期せぬ重大なバグを生み出す可能性があります。
分からない方、どうぞ安心してください。
この記事を読んだ全員が「0.1+0.2≠0.3」を理解できるように分かりやすく説明していきます。
コンピュータが計算を間違う理由
まず、そもそも「0.1+0.2=0.3」で正しい！「0.1+0.2≠0.3」なんてあり得ない！
という方のために、プログラミング言語のフォーマット処理を経ない、コンピュータの計算結果を見てみます。
result = 0.1 + 0.2
print(f"{result:.55f}") # 0.3000000000000000444089209850062616169452667236328125000
コードの右側のコメントが出力結果です。
この通り「0.1+0.2」は「0.3」にはなりません。
なぜこのような現象が起こるのでしょうか。
一言で説明すると「コンピュータは2進数を使っており、10進数から2進数へ正確に変換できない場合がある」からです。
まだ、よく分からないと思いますが、この記事を読み終えた頃には意味が分かるようになっています。理解するために必要な知識は次の2つです。
💡理解するために必要な知識
・ 進法
・ 浮動小数点数
これらを順番に説明していきます。
10進法と2進法の基本
いきなりですが問題です。
2進数の「11011」を10進数に変換してください
この問題を見て、「2進数の1が1で、10が2で、11が3で...」と数えた人は2進法を理解できていません。流し読みせずに、ここから先の説明をしっかり理解しながら読み進めてください。
進法とは
進法とは、数を表す方法です。進数は、進法で表される具体的な数字を指します。
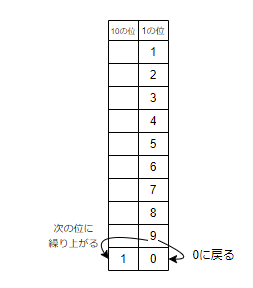
- 10進法：日常生活で一般的に使用される数の表し方です。0から9までの10個の数字を使用し、10進むごとに次の位に繰り上げる方法を指します。
- 2進法：コンピュータ科学で広く使用される数の表し方です。0と1の2つの数字のみを使用し、2進むごとに次の位に繰り上げる方法を指します。
n進法の特徴
$n$進法の特徴
- $0$から$n-1$までの$n$種類の数字を使って数を表す
- 右から順に$n^0,n^1,n^2,....$の位になる
- $n$進むごとに次の位に繰り上がる
10進法
いつも私たちが使っている10進法を例に考えてみましょう。
まず1番目の特徴は「$0$から$n-1$までの$n$種類の数字を使って数を表す」です。10進法は0から9までの10種類の数字を使って数を表しています。
2番目の特徴は「右から順に$n^0,n^1,n^2,....$の位になる」です。10進法では右から順番に、1の位、10の位、100の位、1000の位と呼びます。
3番目の特徴は「$n$進むごとに次の位に繰り上がる」です。
10進むごとに0に戻り、次の位に繰り上がっていることが分かります。
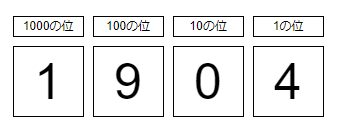
10進法をもう少しよく理解するために、例として「1904」という数字が何を意味しているのか考えてみましょう。
1000の位は1、100の位は9、10の位は0、1の位は4です。
つまり
- 1000が1個
- 100が9個
- 10が0個
- 1が4個
ということを表しているのです。
数式で考えると次のようになります。
$1×1000 + 9×100 + 0×10 + 4×1 = 1904$
$1×10^3 + 9×10^2 + 0×10^1 + 4×10^0 = 1904$
ここでは
$1×10$$^3$ + $9×10$$^2$ + $0×10$$^1$ + $4×10$$^0$
と指数部が規則的になっていることがポイントです。
私たちは普段から10進法を使っているので、なかなか数字の意味を意識することは無いですが、このような考え方になっています。
2進法
次に2進法を考えてみましょう。
$n$進法の1番目の特徴「$0$から$n-1$までの$n$種類の数字を使って数を表す」ですが、2進法は0と1の2種類の数字を使って数を表します。
2番目の特徴「右から順に$n^0,n^1,n^2,....$の位になる」ですが、2進法では右から順番に、1の位、2の位、4の位、8の位となります。
3番目の特徴は「$n$進むごとに次の位に繰り上がる」です。下の表を見ると、2進むごとに、次の位に繰り上がっていることが分かると思います。
| 10進法 | 2進法 | 10進法 | 2進法 | 10進法 | 2進法 |
|---|---|---|---|---|---|
| 0 | 0 | 10 | 1010 | 20 | 10100 |
| 1 | 1 | 11 | 1011 | 21 | 10101 |
| 2 | 10 | 12 | 1100 | 22 | 10110 |
| 3 | 11 | 13 | 1101 | 23 | 10111 |
| 4 | 100 | 14 | 1110 | 24 | 11000 |
| 5 | 101 | 15 | 1111 | 25 | 11001 |
| 6 | 110 | 16 | 10000 | 26 | 11010 |
| 7 | 111 | 17 | 10001 | 27 | 11011 |
| 8 | 1000 | 18 | 10010 | 28 | 11100 |
| 9 | 1001 | 19 | 10011 | 29 | 11101 |
2進数から10進数への変換
2進数の「11011」を10進数に変換する問題を改めて考えてみましょう。
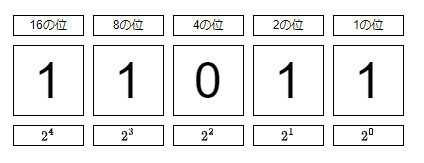
「11011」は5桁で、右から順に1の位、2の位、4の位、8の位、16の位です。
16の位は1、8の位は1、4の位は0、2の位は1、1の位は1です。
つまり
- 16が1個
- 8が1個
- 4が0個
- 2が1個
- 1が1個
ということを表しています。
数式で考えると次のようになります。
$1×16 + 1×8 + 0×4 + 1×2 + 1×1 = 27$
$1×2^4 + 1×2^3 + 0×2^2 + 1×2^1 + 1×2^0 = 27$
このことから2進数の「11011」は、10進数では「27」になることが分かりました。
小数を含む場合の2進数から10進数への変換
小数を含む場合でも考え方は同じです。2進数の「11011.111」を10進数に変換すると、次のようになります。
$1×2^4 + 1×2^3 + 0×2^2 + 1×2^1 + 1×2^0$
$+ 1×2^{-1} + 1×2^{-2} + 1×2^{-3}= 27.875$
📝補足説明
$2^0$は$2^1$を$2$で割った数なので$1$になります。$2^0$を$2$で割った$2^{-1}$は$0.5$になり、そこから更に$2$で割った$2^{-2}$は$0.25$になります。
$2^1÷2=2^0=1$
$2^0÷2=2^{-1}=0.5$
$2^{-1}÷2=2^{-2}=0.25$
$2^{-2}÷2=2^{-3}=0.125$
10進数から2進数への変換
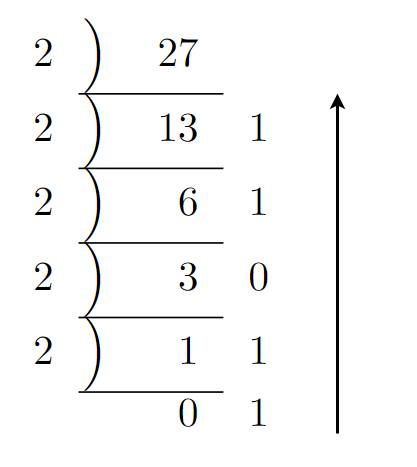
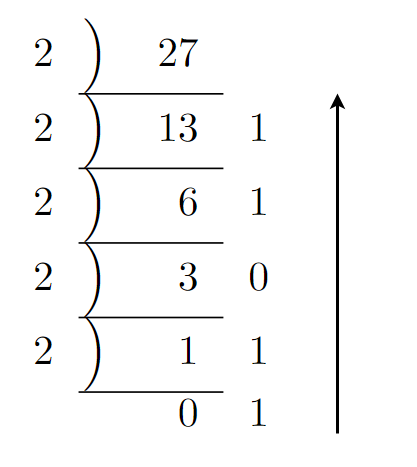
27を2進数へ変換します。
1. 10進数の実数部を2で割ります。
2. その結果の商と余りを記録します。
3. 商が0になるまでこのプロセスを繰り返します。
4. 得られた余りを逆順に並べて、2進数を得ます。
すだれ算という計算方法で変換することが出来ます。
$27÷2=13・・・1$
$13÷2=6・・・1$
$ 6÷2=3・・・0$
$ 3÷2=1・・・1$
$ 1÷2=0・・・1$
得られた余りを逆順に並べ、10進数の「27」を2進数の「11011」へ変換できました。
小数を含む場合の10進数から2進数への変換
0.875を2進数へ変換します。
1. 10進数の小数部を2倍します。
2. 結果の整数部分を記録します。
3. 新しい小数部を再び2倍します。
4. このプロセスを望む精度に達するまで続けます。
小数部分が0になればその後はずっと0が続きますので、計算を終了します。10進数の「0.875」を2進数の「0.111」へ変換できました。
循環小数とは
循環小数とは、同じ数字が決まった順に繰り返す小数のことです。
例えば$1/3$は$0.33333......$となる循環小数です。
0.1を2進数に変換してみましょう。
このとおり小数部分が2,4,8,6でループし、0になりません。10進数の「0.1」は、2進数では$0.0001100110011....$という循環小数になることが分かりました。
次に、0.2を2進数に変換してみましょう。
「0.1」と同様に、小数部分が2,4,8,6でループし、0になりません。このとおり10進数の「0.2」は、2進数では$0.0011001100....$という循環小数になることが分かりました。
上記のとおり、10進数における有限小数0.1と0.2が、2進数では循環小数になってしまいました。
循環小数を計算するには、無限に続く数値をどこかで区切らなければいけません。
$3.1415926....$と無限に続く円周率$π$が$3.14$として用いられているのを見たことがあると思います。これは無限小数である円周率を、小数点第2位まで表現するというルールによって数値を確定させています。同じように、2進数の循環小数も一定のルールで数値を確定させるために、コンピュータ内部で、ある部分で区切られて表現されます。このことを理解するために、浮動小数点数について見ていきましょう。
ここまで理解したこと
- 進法について
- 10進数から2進数、2進数から10進数への変換方法
- 10進数の小数は2進数への変換で循環小数になることがある
浮動小数点数の基本
ここからは日常生活では目にしない用語が多くなり、少し難しくなってきますが、ここを乗り越えればほとんど終わりです。頑張りましょう。
浮動小数点数のルールについては、IEEE（Institute of Electrical and Electronics Engineers）「米国電気電子技術者協会」で制定されています。
小数点数を表すデータ型
浮動小数点数に関する標準規格IEEE754では5つのデータ型が定められています。
この記事では64ビットの倍精度浮動小数点数型に焦点を当てていきます。
浮動小数点数とは
浮動小数点数は、現実世界で見られる広範囲の数値をコンピュータで表現するための方法です。
コンピュータは、「符号(ふごう)」「仮数(かすう)」「基数(きすう)」「指数(しすう)」という4つの部分で浮動小数点数を表します。
倍精度浮動小数点数の内部構造です。
- 符号部(正負を示す部分)：数値の正負を表します。1ビットで構成され、0は正、1は負を意味します。
- 指数部(数の大きさを示す部分)：数値の大きさを決定します。指数部のビット数は浮動小数点数の型によって異なります。倍精度浮動小数点数では11ビットが使われます。指数値に、所定のバイアスを加えて表現します。バイアスについては後述します。
- 基数部：2進数を使うので、基数は必ず2になります。そのため実際のデータでは省略されます。
- 仮数部(数値の詳細を示す部分)：数値の精度を担当します。仮数部のビット数も型によって異なります。倍精度浮動小数点数では52ビットが使われます。仮数部は、基本的に1.xxxxxの形式の数値を表し、先頭の1は省略されます（これを「正規化」と言います）。
📝補足説明
ビットとは？
ビットとはコンピュータの基本的な情報単位です。考え方としては、「はい」か「いいえ」、「オン」か「オフ」など、二つの選択肢を表すのに使います。コンピュータでは、これを「0」と「1」という数字で表現します。
バイトは、8つのビットから成り立っています。たとえば「01010101」のように、0と1が8つ並んだものです。
よく目にする単位として、
1キロバイト(KB)は1024バイト
1メガバイト(MB)は1024キロバイト
1ギガバイト(GB)は1024メガバイト
となっています。
正規化
正規化とは、特定のルールに従って、数値を調整することです。
浮動小数点数における正規化は、仮数部が1から始まるように数値を調整するプロセスです。
正規化をしないとどうなるでしょうか。
浮動小数点数は同じ数値を様々な表現で表すことができます。
10進数の「27.875」には、例えば次のような表現方法があります。
- $27875×10^{-3}$
- $27.875×10^0$
- $0.27875×10^2$
2進数についても同様に、同じ値を様々な表現ができます。
10進数の「27.785」は2進数で「11011.111」です。例えば次のような表現方法があります。
- $11011111×2^{-3}$
- $11011.111×2^0$
- $0.11011111×2^5$
コンピュータが浮動小数点数を効率的に扱い、計算の一貫性と正確性を保つためには、異なる方法で表現可能な数値を、一貫した形式に統一する必要があります。
ここで活躍するのが、正規化です。
2進数の「11011.111」を仮数部が1から始まるように正規化すると次のようになります。
$1.1011111×2^4$
正規化により、様々な表現方法を統一化することができるのです。
さて、正規化された2進数の「$1.1011111×2^4$」は、コンピュータではどのようなデータになっているのでしょうか。
先に答えを出すと次のようになっています。
符号部:0
指数部:10000000011
仮数部:1011111000000000000000000000000000000000000000000000
浮動小数点数：0-10000000011-1011111000000000000000000000000000000000000000000000
符号部
数値の正負を1ビットで表します。0は正、1は負を意味します。今回は正の数値なので0が入ります。
指数部
数値の大きさを11ビットで表します。指数値にバイアスを加えた後、2進数に変換します。バイアスとは、指数部の値を非負の範囲に調整するために加えられる固定値です。倍精度浮動小数点数では、バイアスは1023というルールになっています。
正規化された「$1.1011111×2^4$」の指数部は$4$で、$1023$のバイアスが加えられます。
$4+1023$の和である$1027$を2進数変換すると$10000000011$になります。
すだれ算がしっくりこない方のために違う方法で変換してみます。
$□×2^{10}+□×2^9+□×2^8+□×2^7+□×2^6+□×2^5$
$+□×2^4+□×2^3+□×2^2+□×2^1+□×2^0$
$=1027$
上の式が成立するように$□$を埋めれば1027を2進数に変換した値を得られます。
1027に1番近く、1027以下の2の累乗は$2^{10}$なので、$□×2^{10}$からスタートします。
2進数なので$□$には1か0が入ります。
$2^{10}$を使わないと1023までしか表現できないので、$□×2^{10}$に1を入れます。
$1027-1024$で残りは3、$□×2^1+□×2^0$に1を入れれば1027の完成です。
$10000000011$となりました。
次に、バイアスを使用する理由を説明します。
通常、指数部は符号付きの数値($n$乗を$+$でも$-$でも表すことが可能)ですが、浮動小数点数の指数部は符号なしです。バイアスを加えることで、指数部の実際の値が負になる場合でも、符号なしの数値として表現できます。これにより、浮動小数点数はより広範囲の数値を効率的に表現できます。
仮数部
数値の精度を52ビットで表します。基本的に1.xxxxxの形式の数値を表し、先頭の1は省略します。
つまり、正規化された「$1.1011111×2^4$」の仮数部（小数部）は1.xxxxxのxxxxxの部分なので、$1011111$となり、残りのビットを0で埋めています。
$1011111000000000000000000000000000000000000000000000$となりました。
変換方法の確認
1. 2進数に変換
2. 正規化
3. 符号部
4. 指数部
5. 仮数部
27.875を倍精度浮動小数点数で表す方法を再度確認しましょう。変換のプロセスは次のようになります。
2進数に変換
27.875を2進数に変換すると、「11011.111」になります。
正規化
「11011.111」を1.xxxxxの形式に変換すると、
$1.1011111×2^4$になります。
指数部
倍精度浮動小数点数では、指数部に1023のバイアスが加えられます。
4(実際の指数)+1023(バイアス)=1027。これを2進数に変換すると、10000000011になります。
仮数部
正規化された数「$1.1011111×2^4$」の仮数部（小数部）は、1011111です。
倍精度浮動小数点数の仮数部は52ビットなので、残りのビットを0で埋めます。
組み立て
符号部（0）、指数部（10000000011）、仮数部（1011111...（残りは0で埋める））を組み合わせます。
符号部:0
指数部:10000000011
仮数部:1011111000000000000000000000000000000000000000000000
浮動小数点数: 0-10000000011-1011111000000000000000000000000000000000000000000000
ここまで、10進数を2進数の倍精度浮動小数点数として表す方法を説明しました。
ここまで理解したこと
- 進法について
- 10進数から2進数、2進数から10進数への変換方法
- 10進数の小数は2進数への変換で循環小数になることがある
- 🆕 浮動小数点数の表し方
0.1 + 0.2 ≠ 0.3問題
さて本題に戻りましょう。
ここからは今までの内容を踏まえて、「0.1+0.2」を見ていきたいところですが、その前に丸めについて説明します。
丸め
仮数部が循環小数の場合、決められた52ビットに収まりきりません。IEEE754では、52ビットで表すためのルールが定められています。表現可能な2つの数値の中間点であった場合、最も近い偶数に丸めるという方法です。
一番身近な丸めの例は四捨五入ですが、浮動小数点数の丸めには四捨五入は採用されていません。
言葉の説明だけだと分かりづらいと思うので、まずは10進数で考えてみましょう。
整数になるように丸めると次のようになります。
1. 中間点より大きい
100.xxxxを整数で表現すると100か101になります。中間点は100.5です。
例えば「100.578990」は中間点より大きいので101になります。
2. 中間点より小さい
例えば「100.222222」は中間点より小さいので100になります。
3. 中間点
「100.5」の場合、100と101の中間点になります。
この場合は、最も近い偶数に丸めるので100になります。
2進数ではどうでしょう。
1. 中間点より大きい
100.xxxxを整数で表現すると100(10進数の4に相当)か101(10進数の5に相当)になります。
中間点は100.1（10進数の4.5に相当）です。
例えば「100.11111」は中間点より大きいので101になります。
2. 中間点より小さい
例えば「100.00110011」は中間点より小さいので100になります。
3. 中間点
「100.1」の場合、100と101の中間点になります。
この場合は、最も近い偶数に丸めるので100になります。
仮数部の丸め処理のルール
- 丸めたい数値が表現可能な2つの数値の中間点より大きい場合、丸めたいビットの次のビットを切り上げる。
- 丸めたい数値が表現可能な2つの数値の中間点より小さい場合、丸めたいビットの次のビットを切り捨てる。
- 丸めたい数値が表現可能な2つの数値の中間点の場合、最も近い偶数に丸める。
丸め処理について理解したところで、「0.1+0.2」の計算に入りましょう。
0.1と0.2をそれぞれ浮動小数点数で表します。
まず「0.1」を変換します。
符号部
正なので符号部は0です。
指数部
指数部は-4なので、バイアス1023を足した和1019を2進数変換して$01111111011$となります。
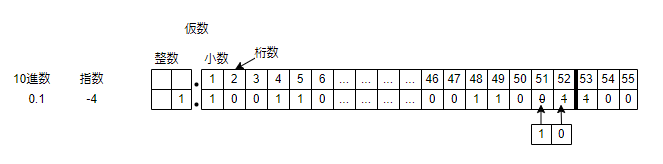
仮数部
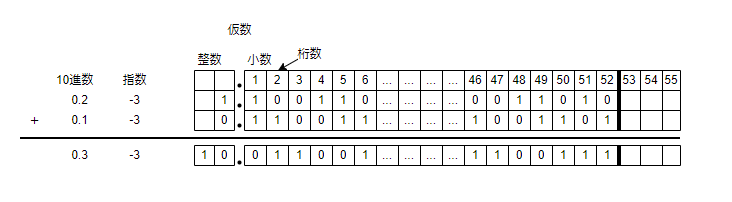
循環小数のトピックで計算した通り「0.1」を2進数に変換すると$0.000110001100011....$という循環小数になります。倍精度浮動小数点型の決まりで、仮数部を52ビットにする必要があります。53ビット目が1で、画像では隠れていますが、56ビット目にも1がくるので、53ビット目を繰り上げます。そうすると仮数部は$1001100110011001100110011001100110011001100110011010$で定まります。
「0.1」の2進数への変換ができました。これをさらに10進数に変換するとどうなるでしょうか。
$1.1001100110011001100110011001100110011001100110011010×10^{-4}$
これを10進数に変換する計算は次のとおりです。$1×2^{-1}+0×2^{-2}+0×2^{-3}+1×2^{-4}.....+0×2^{-50}+1×2^{-51}+0×2^{-52}×10^{-4}$
計算過程は省きますが
$0.1000000000000000055511151231257827021181583404541015625$が得られます。
10進数の「0.1」を2進数に変換して、10進数に変換し直す過程はこのようになっているのです。
実際に次のプログラムを実行すると同じ結果が得られます。
# 10進数→2進数→10進数の結果
print(f"{0.1:.55f}") # 0.1000000000000000055511151231257827021181583404541015625
符号部:0
指数部:01111111011
仮数部:1001100110011001100110011001100110011001100110011010
浮動小数点数：0-01111111011-1001100110011001100110011001100110011001100110011010
10進数へ変換:0.1000000000000000055511151231257827021181583404541015625
次に「0.2」を変換します。
符号部
正なので符号部は0です。
指数部
指数部は-3なので、バイアス1023を足した和2020を2進数変換して$01111111100$となります。
仮数部
こちらも循環小数のトピックで計算した通り「0.2」を2進数に変換すると$0.0011001100....$という循環小数になります。「0.2」は「0.1」の2倍なので指数部の乗数が1大きくなるだけで、仮数部は0.1と同じになります。そのため、仮数部は$1001100110011001100110011001100110011001100110011010$となります。
ここから10進数に変換する方法は0.1のときと同じなので省きますが、
$0.2000000000000000111022302462515654042363166809082031250$が得られます。
実際に次のプログラムを実行すると同じ結果が得られます。
# 10進数→2進数→10進数の結果
print(f"{0.2:.55f}") # 0.2000000000000000111022302462515654042363166809082031250
符号部:0
指数部:01111111100
仮数部:1001100110011001100110011001100110011001100110011010
浮動小数点数：0-01111111100-1001100110011001100110011001100110011001100110011010
10進数へ変換:0.2000000000000000111022302462515654042363166809082031250
0.1と0.2を2進法の浮動小数点数に変換できたので、最後に和を求めましょう。
1. 指数を大きい方に合わせる。
2. 仮数部を足す。
3. 合計値を正規化する。
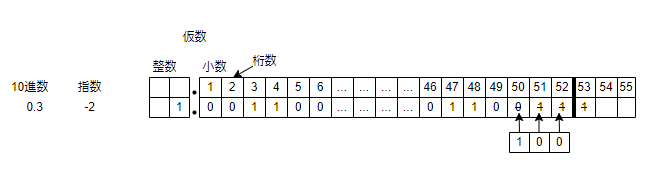
4. 丸め処理をする。
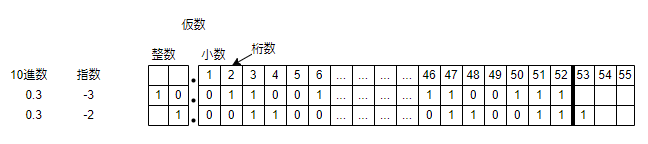
① 0.1を0.2の指数-3に合わせます。画像の通り右にひとつずらすだけです。ここでも丸め処理を行います。53ビット目が0なので切り捨てます。
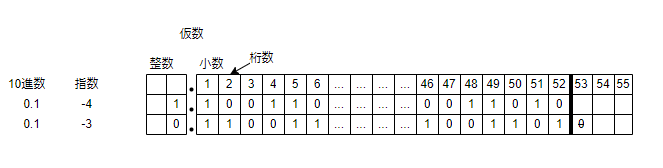
📝補足説明
指数を-4から-3にするとは？
10進数で考えると分かりやすいと思います。
$1.001100×10^{-4}$
$=(1.001100÷10)×(10^{-4}×10)$
$=0.1001100×10^{-3}$
指数調整のため10掛けた代わりに、仮数を10で割っているだけです。
② 仮数部を足します。
📝補足説明
2進数の足し算
💡ポイント「2進むごとに繰り上がる」
111(10進数で7)+110(10進数で6)=1101(10進数で13)
100(10進数で4)+011(10進数で3)=111(10進数で7)
同じ位がどちらも1なら繰り上がります。
③ 合計値を正規化(1.xxxxxの形式に変換)します。
④ 丸め処理をします。
最後に10進数に変換すると、0.3000000000000000444089209850062616169452667236328125000になります。実際に次のプログラムを実行すると同じ結果が得られます。
# 10進数→2進数→10進数の結果
result = 0.1 + 0.2
print(f"{result:.55f}") # 0.3000000000000000444089209850062616169452667236328125000
以下が計算結果のまとめです。
符号部:0
指数部:01111111101
仮数部:0011001100110011001100110011001100110011001100110100
浮動小数点数:0-01111111101-0011001100110011001100110011001100110011001100110100
10進数へ変換:0.3000000000000000444089209850062616169452667236328125000
人間は10進数で計算しますが、コンピュータは入力された10進数を2進数に変換した上で計算を行い、その後10進数に変換し直して結果を表示します。10進数を2進数に変換する過程で仮数部の丸め処理が行われるため、誤差が生じます。これが原因で、人間が行う計算結果と、コンピュータが行う計算結果には差が生じるのです。
まとめ
主なポイントは以下の通りです。
- コンピュータでは、数値は2進数で表現されます。
- 10進数での簡単な数(0.1や0.2など)も、2進数では循環小数になることがあります。
- 循環小数の丸め処理を行うことで誤差が生じます。
- 誤差が出た状態で2進数を10進数へ変換し直すと、人間が行う計算結果とコンピュータが行う計算結果には差が生じます。
- 0.1 + 0.2 が 0.3 にならない現象は、これらの2進数表現の制約によるものです。
これらの知識は、予期せぬバグを避け、より信頼性の高いソフトウェアを開発する際に役立ちます。浮動小数点数の扱いを理解することは、複雑な計算やデータ処理において重要なスキルです。皆さんが今後のプロジェクトでこの情報を活用し、より堅牢なプログラムを作成することを願っています。
最後に
弊社では、経験の有無を問わず、社員やインターン生の採用を行っています。
興味のある方はこちらをご覧ください。