ユニークビジョン株式会社 Advent Calendar 2024 12月17日の記事です。
そういえば3年ほど積んでいる本で『作って動かすALife』というのがあったんだったと思い出したので、遊んでみます。
ずっと読まずに積んでいた本ですが、少し思い入れのある本です。
おそらく、初めて買った技術書です。当時プログラミングをまったくやったことのなかった私は環境構築でつまづいて、この本を押入れの奥底にしまったのでした。
ALifeとは
Artificial Life(人工生命)の略です。ALife(エーライフ)と読みます。
コンピュータを使って生命をシミュレートし、そこから生命とはなにかを探る分野です。
やってみる
本書で使用するプログラムはすべてGitHubで公開されています。
これに従って実際にALifeを動かしてみます。
Gray-Scott モデル
$ cd chap02
$ python gray_scott.py
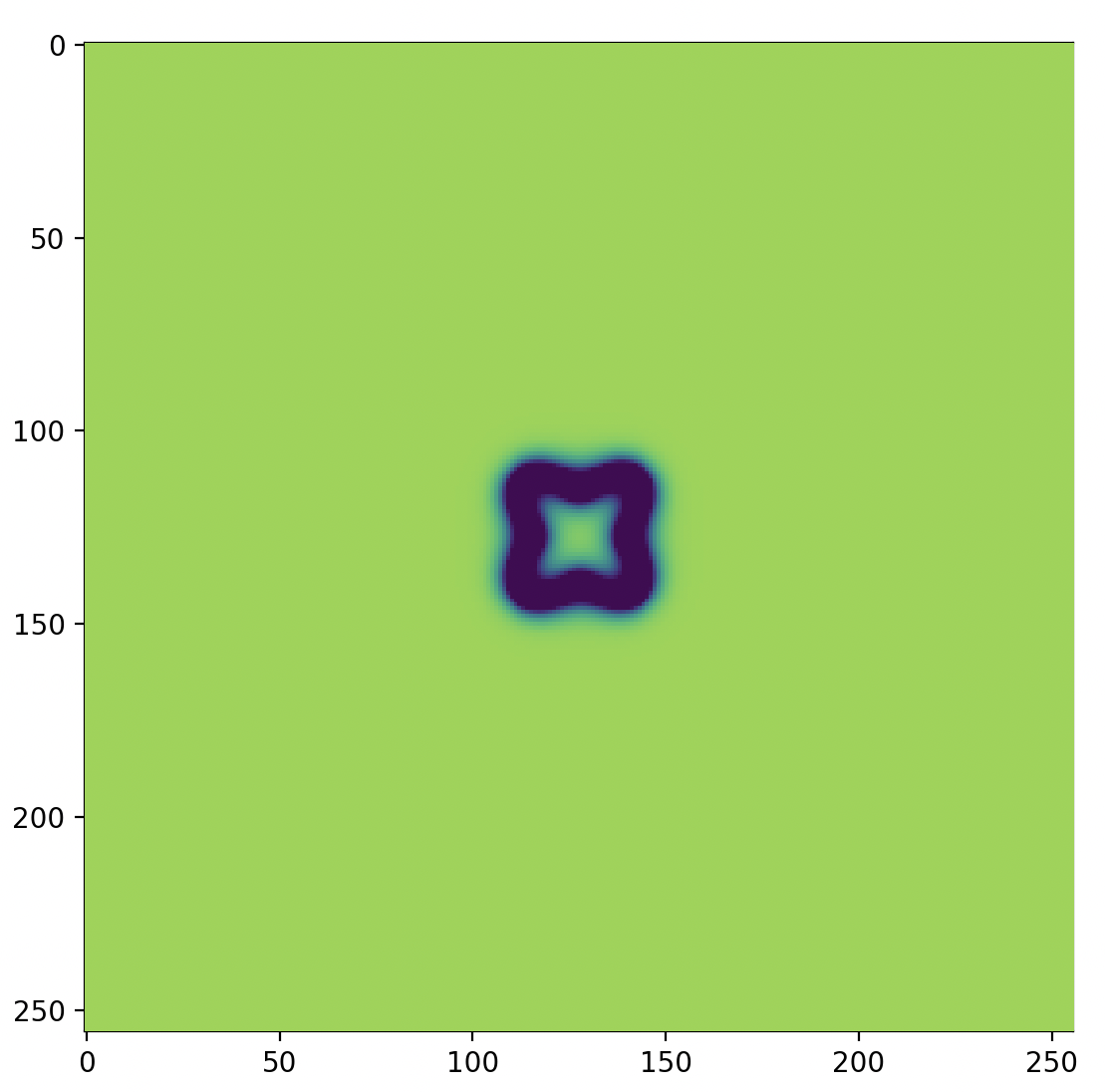
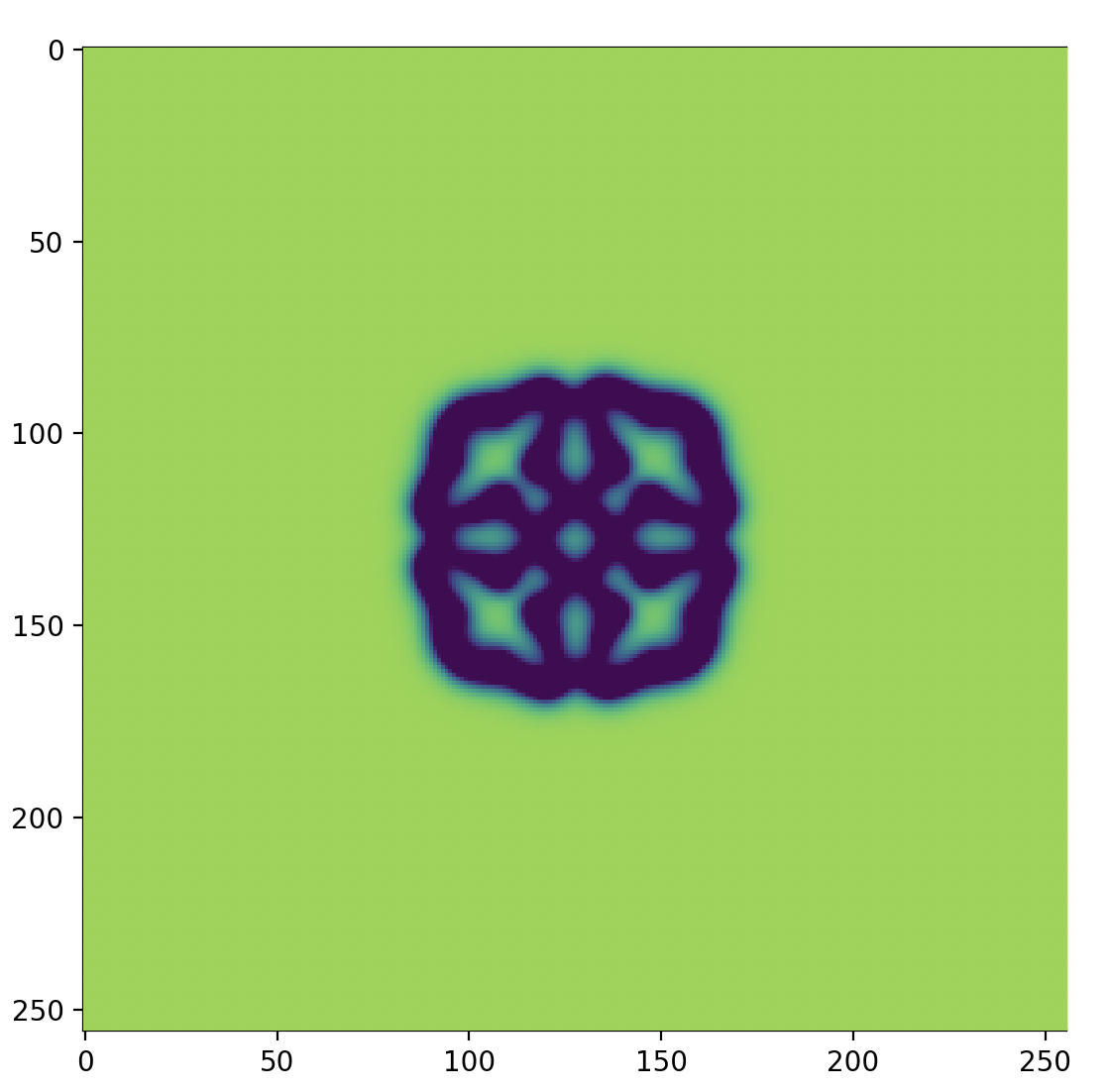
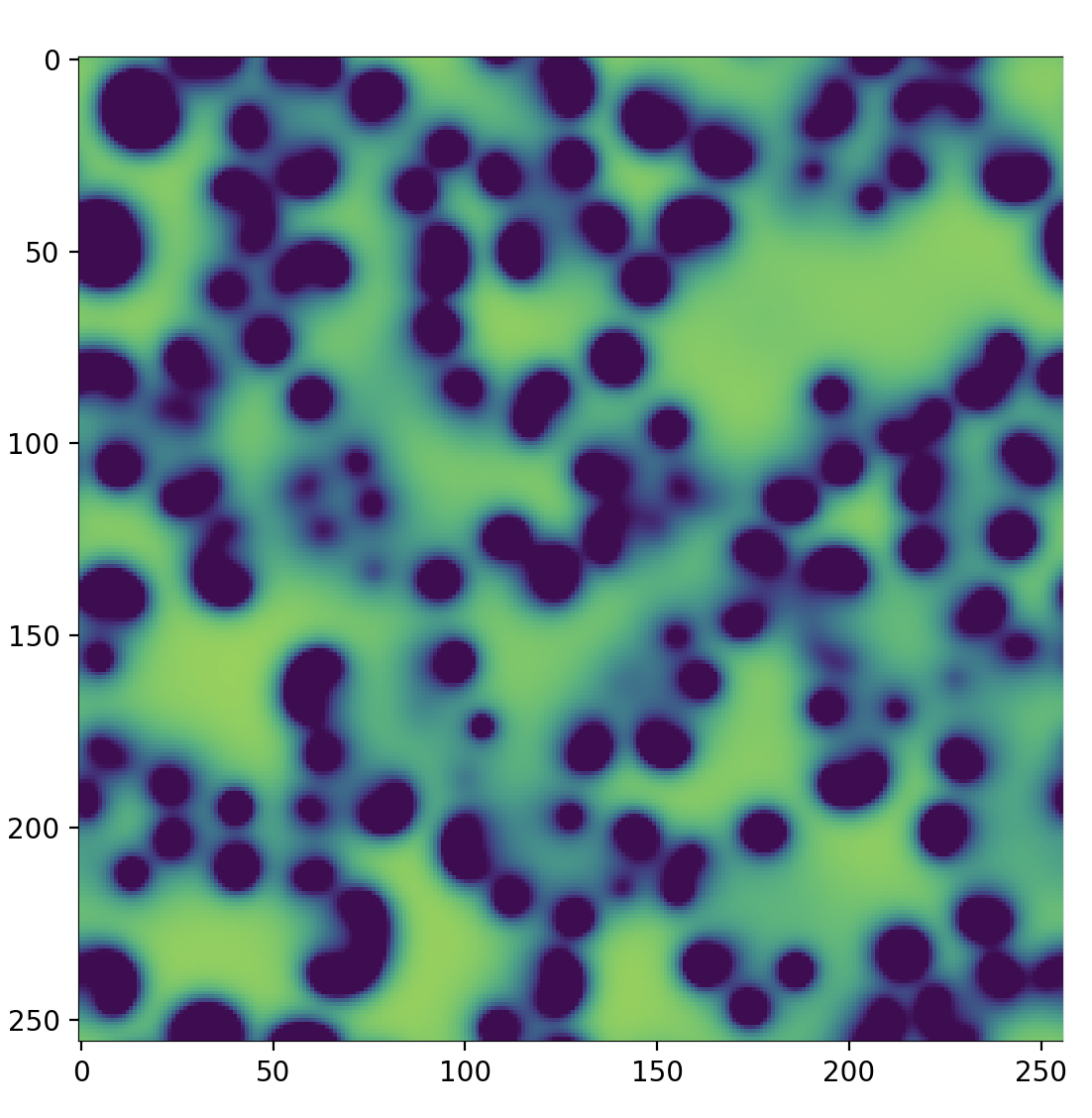
これを実行するとビジュアライザが開き、以下のような模様が描画されます
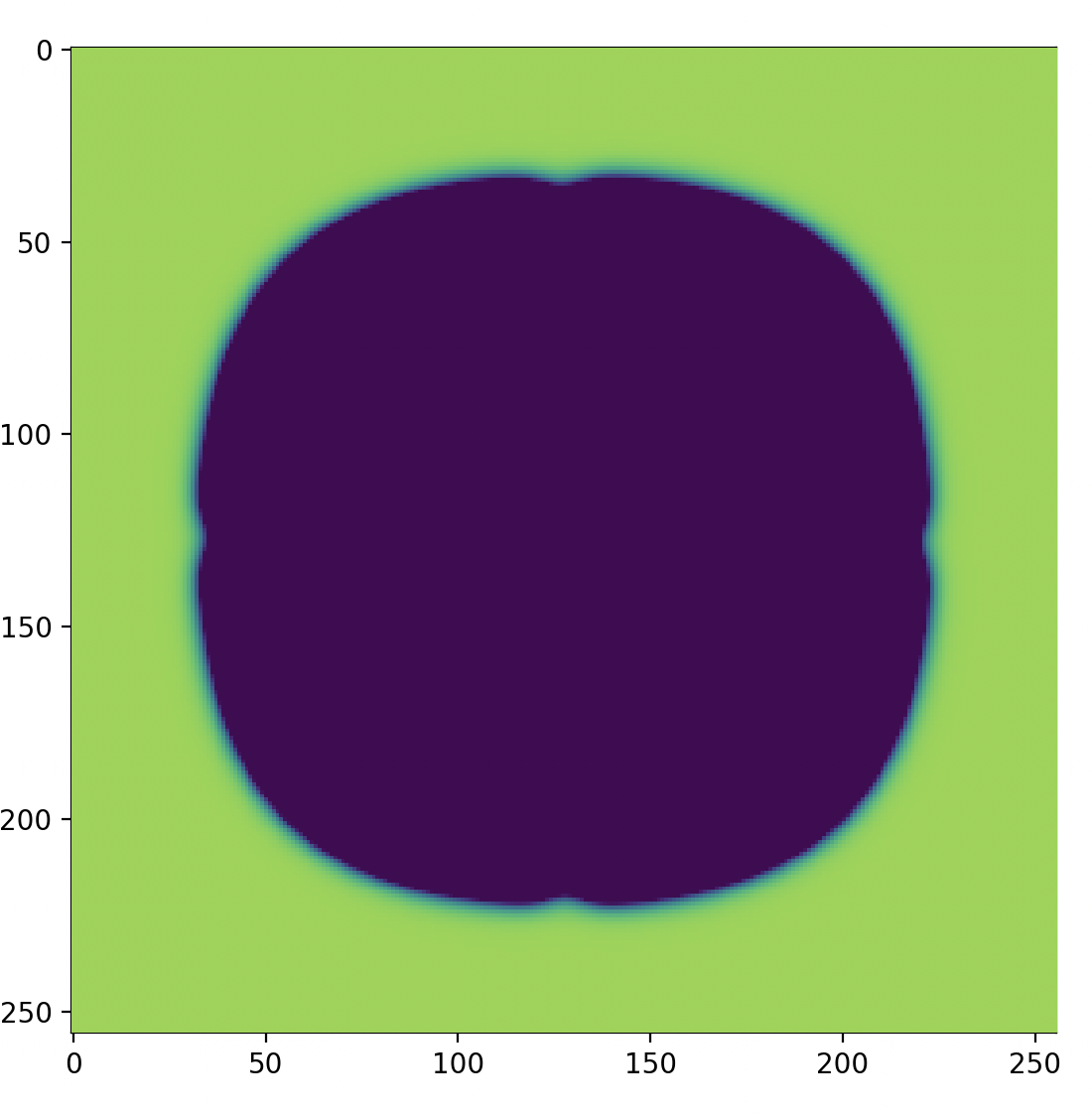
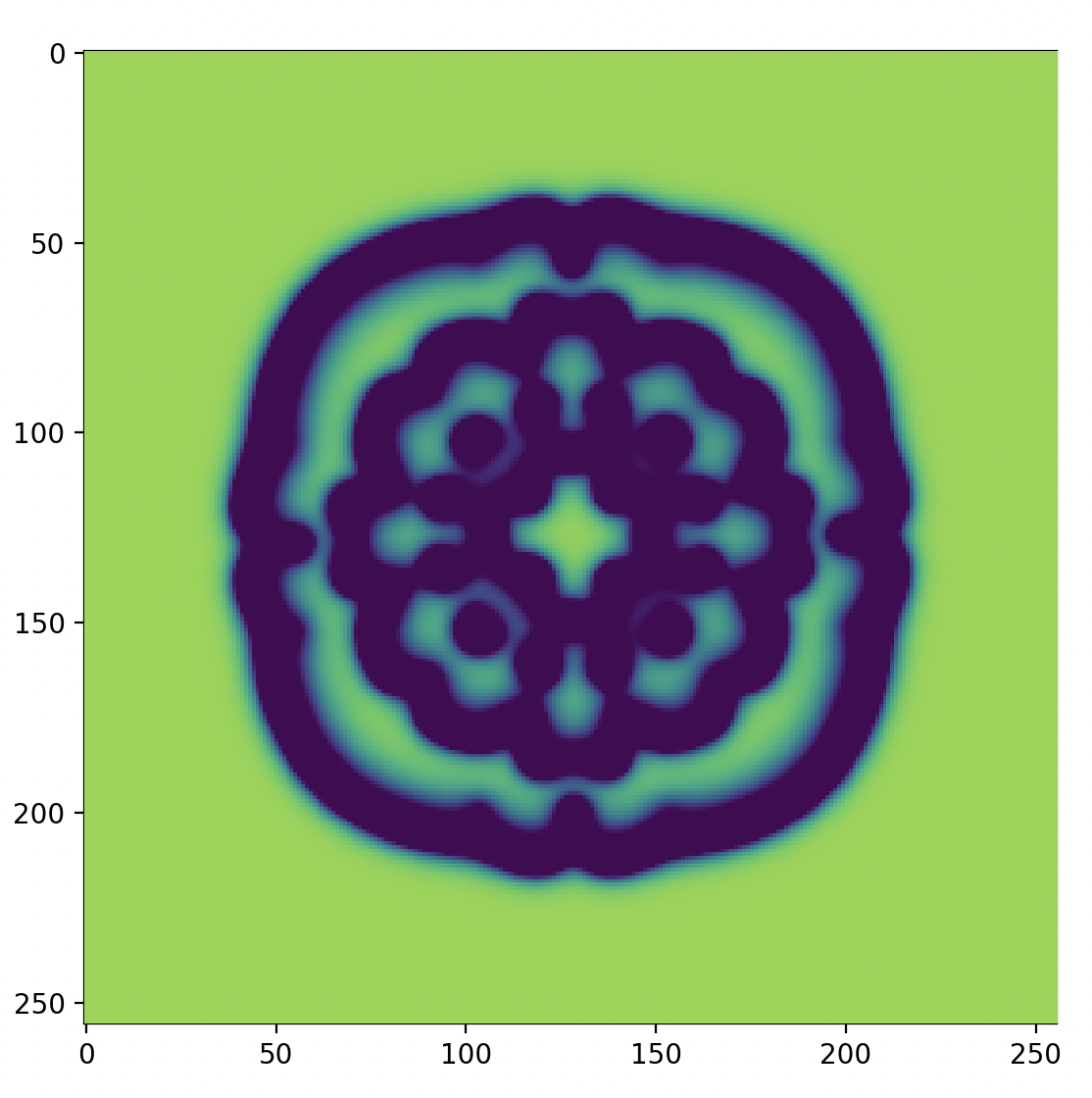
はじめ、中心に花のような模様が描画され、それが次第に枝を伸ばすように広がっていきます。
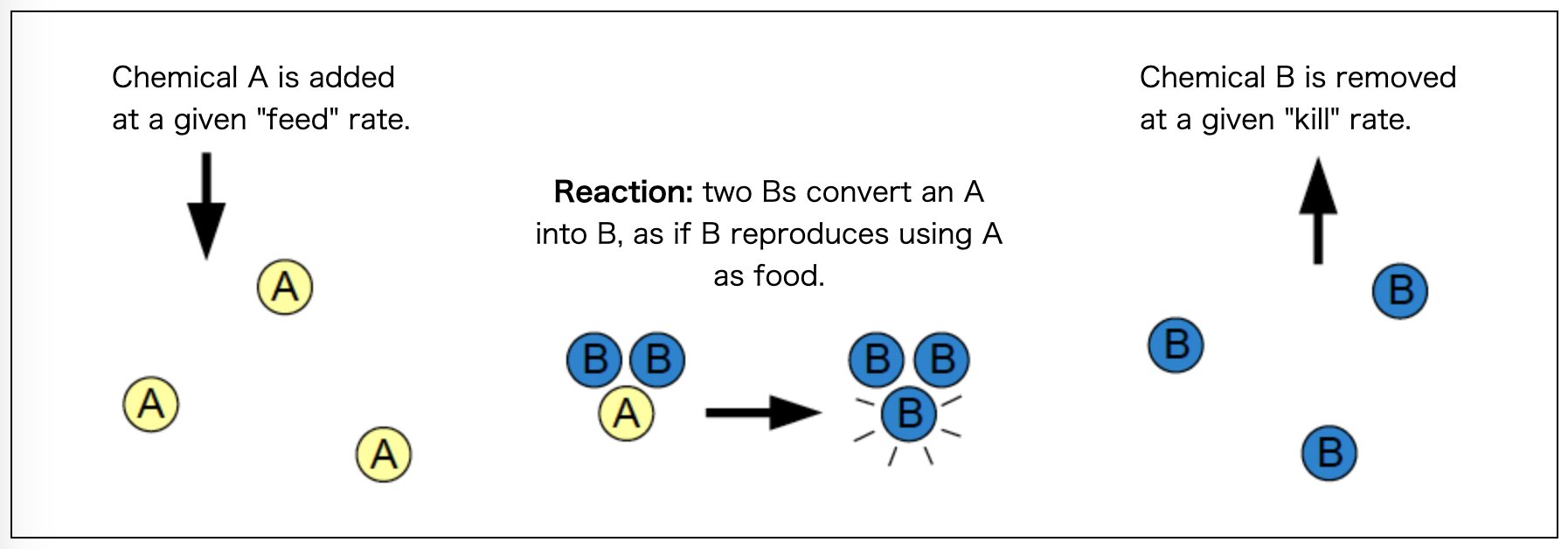
Gray-Scott モデルは単純な化学反応をモデル化したものです。「反応拡散系」と呼ばれる化学反応のひとつです
(https://www.karlsims.com/rd.html より)
これを二次元のグリッドで表現したものが先ほどのパターンです。
グリッドの各マスは物質a,bの濃度を持っています。
さて、このパターンを描画しているプログラムを見ていきます。
SPACE_GRID_SIZE = 256
dx = 0.01
dt = 1
VISUALIZATION_STEP = 8 # 何ステップごとに画面を更新するか。
まず、初期条件を決めます。
SPACE_GRID_SIZE はシミュレーション空間のグリッド数です。
dx はグリッド1目盛りに対するモデル空間の長さです。小さければ細かくシミュレーションでき、大きければ粗いシミュレーションになります。
dtはdx同様、シミュレーション1ステップごとのモデルのステップ数です。
Da = 2e-5
Db = 1e-5
f, k = 0.04, 0.06
さらに定数を設定します。
Da, Db は物質a,bの拡散の速度です。先ほどの化学反応の図の2つの物質にあたります。
そしてこのモデルで最も重要な定数f,kはfeedとkillを示し、物質aの補充と物質bの減量に関わります。
# 初期化
a = np.ones((SPACE_GRID_SIZE, SPACE_GRID_SIZE))
b = np.zeros((SPACE_GRID_SIZE, SPACE_GRID_SIZE))
# 中央にSQUARE_SIZE四方の正方形を置く
SQUARE_SIZE = 20
a[SPACE_GRID_SIZE//2-SQUARE_SIZE//2:SPACE_GRID_SIZE//2+SQUARE_SIZE//2,
SPACE_GRID_SIZE//2-SQUARE_SIZE//2:SPACE_GRID_SIZE//2+SQUARE_SIZE//2] = 0.5
b[SPACE_GRID_SIZE//2-SQUARE_SIZE//2:SPACE_GRID_SIZE//2+SQUARE_SIZE//2,
SPACE_GRID_SIZE//2-SQUARE_SIZE//2:SPACE_GRID_SIZE//2+SQUARE_SIZE//2] = 0.25
# 対称性を壊すために、少しノイズを入れる
a += np.random.rand(SPACE_GRID_SIZE, SPACE_GRID_SIZE)*0.1
b += np.random.rand(SPACE_GRID_SIZE, SPACE_GRID_SIZE)*0.1
コメントの通りですが、初期条件として中央に正方形を置き、そこから反応・拡散する様子を見ていきます
def update(frame):
global a, b
for i in range(VISUALIZATION_STEP):
# ラプラシアンの計算
laplacian_a = (np.roll(u, 1, axis=0) + np.roll(u, -1, axis=0) +
np.roll(u, 1, axis=1) + np.roll(u, -1, axis=1) - 4*u) / (dx*dx)
laplacian_b = (np.roll(v, 1, axis=0) + np.roll(v, -1, axis=0) +
np.roll(v, 1, axis=1) + np.roll(v, -1, axis=1) - 4*v) / (dx*dx)
# Gray-Scottモデル方程式
dudt = Du*laplacian_u - a*b*b + f*(1.0-a)
dvdt = Dv*laplacian_v + a*b*b - (f+k)*b
a += dt * dadt
b += dt * dbdt
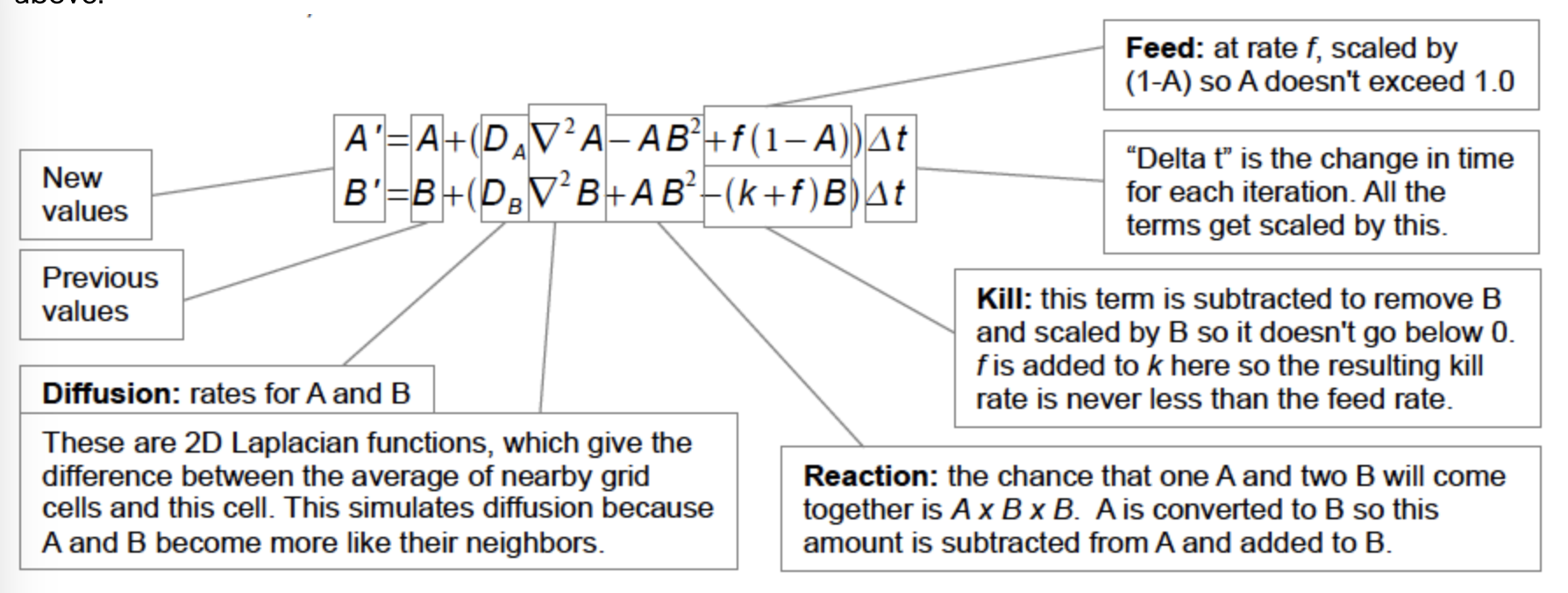
ここがGray-Scott モデルの本質です。
コメントにあるGray-Scottモデル方程式をまず確認します
(https://www.karlsims.com/rd.html より)
プログラムでは第1項は省略されています。
第2項は拡散を表しています。先ほど設定した拡散係数とラプラシアンを掛け算しています。
第3項は化学反応です。物質Aが失われて物質Bが生成される反応です。
第4項はAの補充とBの減量です。上式では1-Aとなっていることからわかるように、Aが増えると補充される量が減り、減ると補充量は増えるような、バランスをとっています。下式ではBに比例していることからBは増えすぎると減量される量も増えるようになっています。
AとBは、拡散しつつ、反応により増減し、さらに全体量に応じて補充・減量される、というモデルです。
アレンジ
Gray-Scott モデルのロジックはこれで以上です。
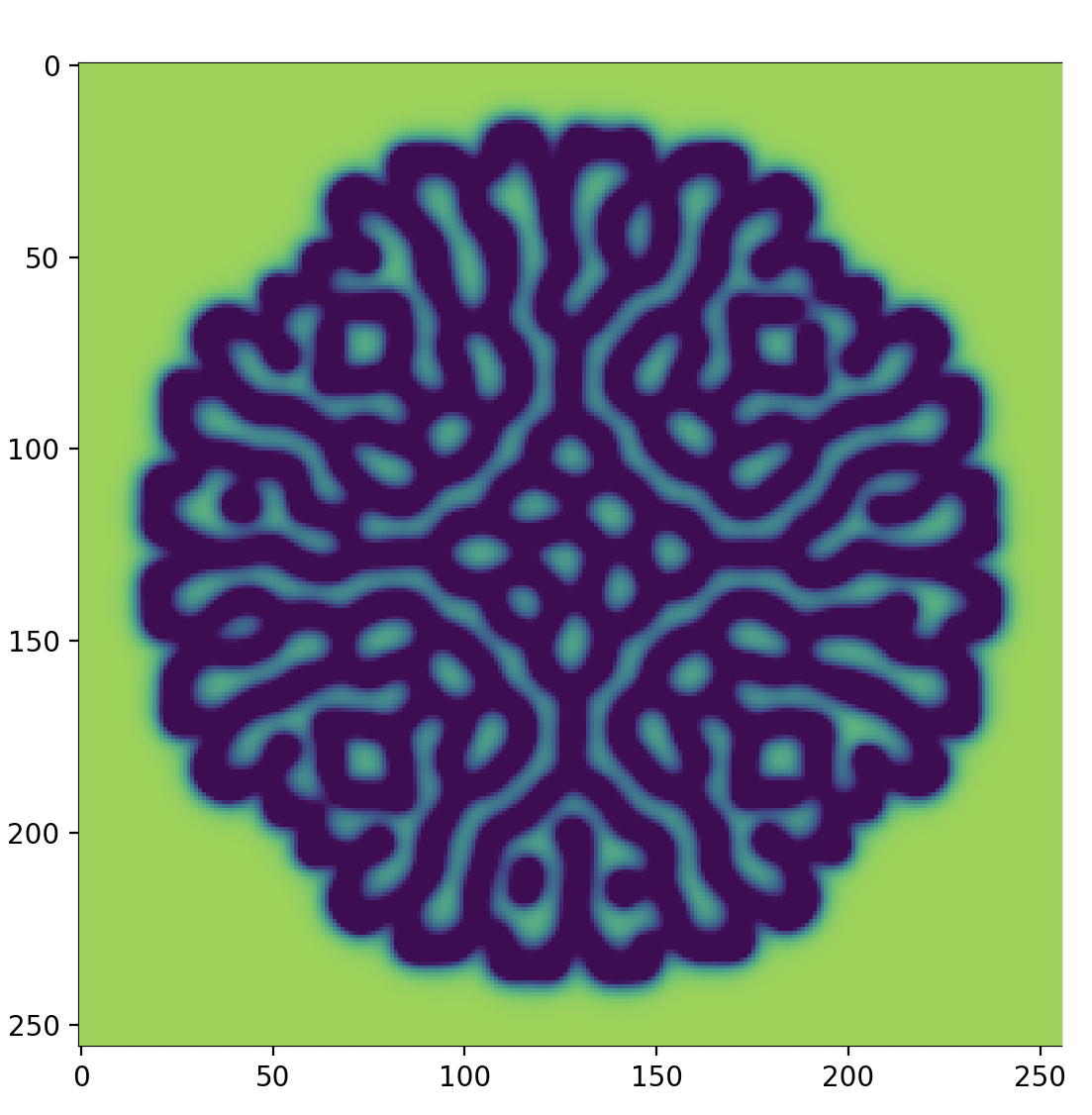
このモデルのおもしろいところは先ほど設定した係数を少し変えるだけで振る舞いを大きく変えるところです
f, k = 0.04, 0.06 # amorphous
aの補充とbの減量を司るこの係数をいくつか変えてみましょう。
先ほどの例ではamorphousでした
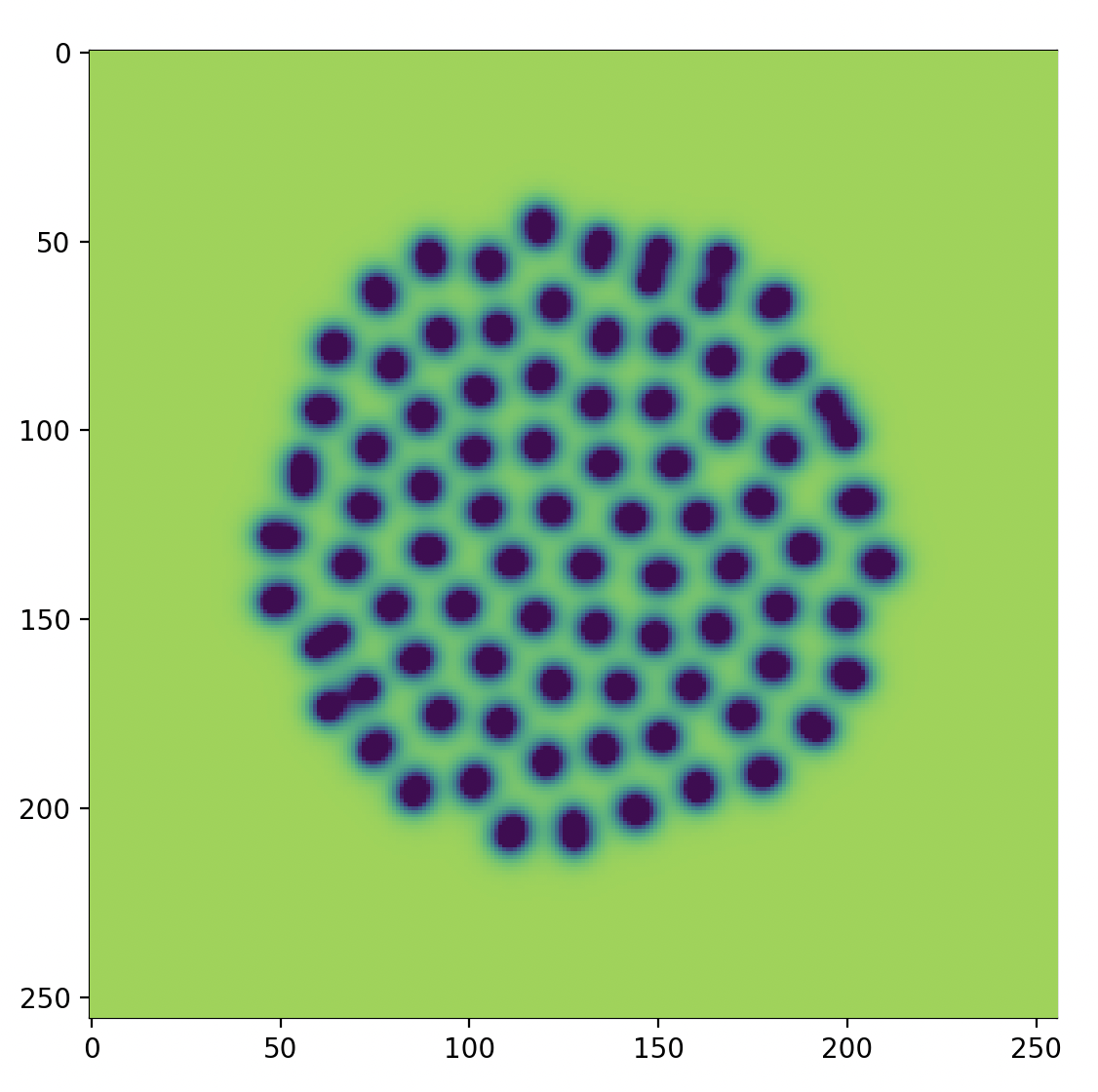
f, k = 0.035, 0.065 # spots
シンプルな斑点です。
f, k = 0.012, 0.05 # wandering bubbles
動かすとわかりますが、泡が生まれては弾け、見たいな動きをしています。
f, k = 0.025, 0.05 # waves
わかりにくいですが、中心から波が出ているように見えなくもないです。
f, k = 0.022, 0.051 # stripe
縞...っぽい。
aの補充とbの減量のパラメータを少しいじるだけで全く異なるパターンが描き出されます。
まとめ
読んでみると、コンピュータサイエンスの方面というより、生物・化学・数学方面の欲が満たされるような本でした。
実装せずともシミュレーションは動くし、軽くコードを確認するくらいで読み進めていけるので手軽でいい本です。