はじめに
アプリケーションが重くなる時、どこから調査しますか?どうやって解決しますか?
リファクタリングしてソースコードの行数だけ減らせば処理が軽くなるという考え方を耳にすることもありますがその根拠が薄いと毎回思っちゃいます。
代わりに自分の勉強からまとめたパフォーマンス診断の3ステップをご紹介します!
セオリーの部分読んでいただければリファクタリングだけはパフォーマンスの改善にならない理由がわかります。
Laravelに全く親しみがない方にもお役に立つと思います。
パフォーマンス3ステップ診断:
- データ使ってボトルネックを見つける
- 計算複雑度を分析する
- 計算複雑度を軽減する
目次
データ使ってボトルネックを見つける
If you fear performance may be a problem, I recommend that you conduct some experiments to prove that it will be a problem. Once proven, and only once proven, you should start considering how to speed things up.
パフォーマンスに問題があるのではないかと心配な場合は、実験を行って問題があることを証明することをお勧めします。 証明されたら、証明された場合だけは、パフォーマンス改善の方法を検討し始めて良いです。
– Robert Martin (Agile Software Development, Principles, Patterns, and Practices)
アンクルボブのお言葉に従えば良い:証拠のない最適化は自分でトラブルを作ることに違いありません。まずはデータから始めてください。
Laravelの場合、Debugbarがおすすめです。リクエストごとにデータベースのタブ見て、クエリ数が多すぎるかどうか、または 1 つのクエリに時間がかかりすぎるかどうかを確認してください。ウェブアプリケーションにおいては一番よく見るボトルネックです。
重いページがわからない場合、ウェブサーバのログ見て一番アクセスが多いページを特定する。ページのどのAPIが重いか、もしくはフロントエンドかバックエンドが原因かわからない場合、Google Chromeのネットワークタブ見て判断する。パフォーマンスの問題を再現できない場合、本番環境と同じ件数までデータベースをシードしてください。
とにかく、デバッグと同じくデータ使って絞り込んでください。ボトルネックが分からない限りパフォーマンスの最適化が出来ません。リファクタリングだけはパフォーマンス改善できないの1つ目の理由はボトルネックとその証拠になるデータはまず提出していないからです。
計算複雑度を分析する
計算複雑度理論さえ理解すれば、99%のパフォーマンス問題が解決できます。この理論は何か簡単に言うと、インプットデータが増加すると、実行時間 (と使用メモリ) がどのように増加するかの考え方です。
nをインプットデータの長さとします。何のインプットかと言うと、ステップ1からわかります!大きいテーブルに対してクエリが時間かかりすぎる場合、nはそのテーブルの件数になります。アップロードファイルが大きすぎる場合、nはそのファイルのバイト数になります。長いリストに対してループ実行している場合、nはそのリストの長さです。
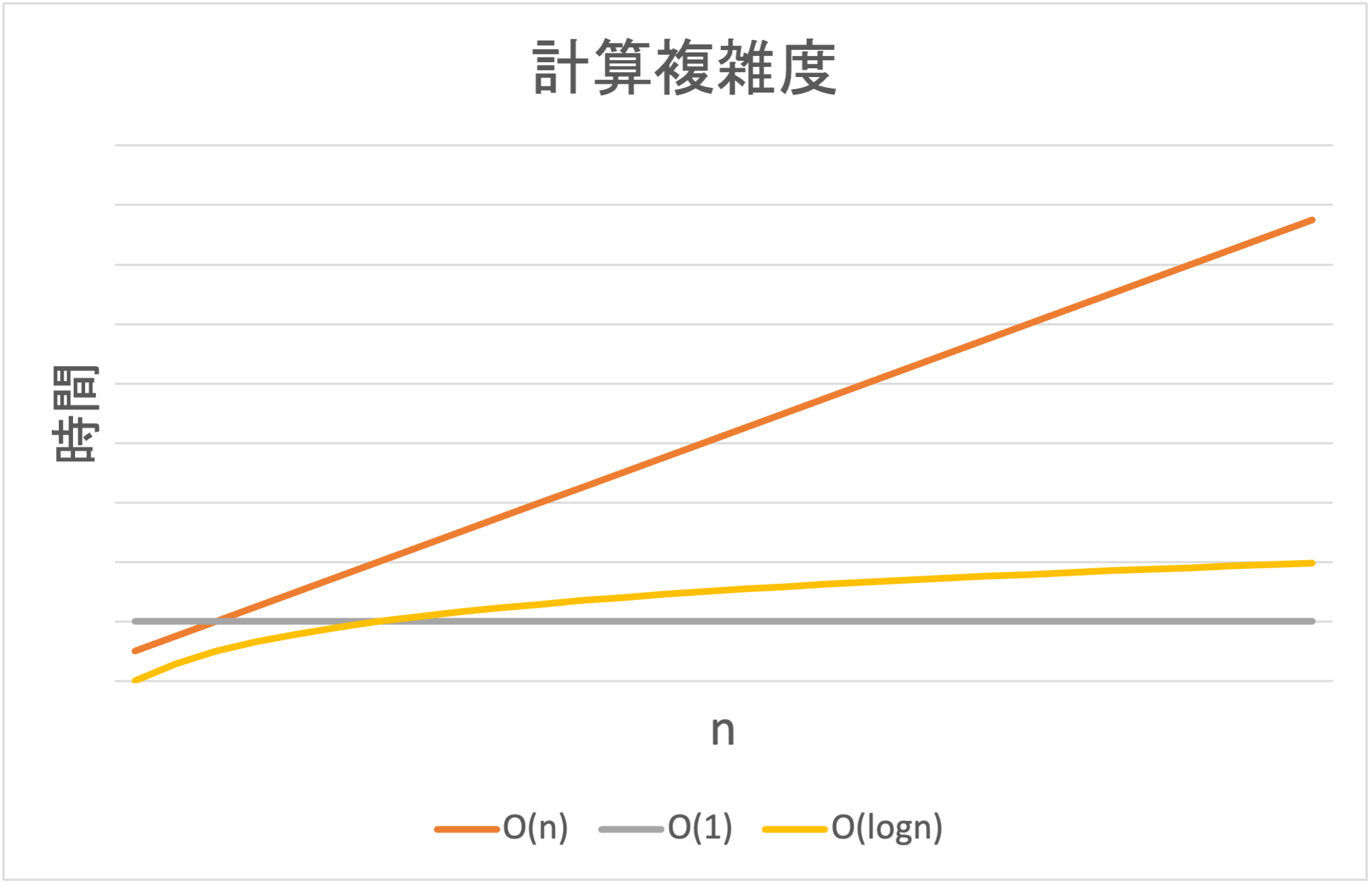
次ですが、nと実行時間の関係性をO記号で表します。例えば、O(f(n))がO(2n)の場合、アプリの実行時間がn * 2と比例します。知っておいて欲しいO関数は次のとおりです。
O(1)
まず、O(1)は最高です。nのサイズに関係なく実行時間が一定の時です。ループがない時は大体O(1)になります。1000行の関数でもO(1)である可能性があります。実際、O(1000)はO(1)と等しいと言います。nが無限になると1000と1は大して変わらないからです。つまり、ソースコードを1000行から1に片付いても、パフォーマンスを改善出来たとは言えません。
O(logn)
続いてO(logn)も結構速いです。ソートされたリストまたはハッシュインデックスを検索している場合、O(logn)になります。 (計算は省いておきますが、二項検索だからです。)この場合、実行時間はnに応じて増加はしますが、無視できるほどとして良いです。なので、テーブルを正しくインデックスしていると、テーブルのサイズが倍になっても検索時間が1ループしか増えない状態が出来ます。
O(n)
最後に、O(n)は実行時間がnに比例する時です。ちなみに、O(1000n)はO(n)に等しいです。ループが配列の全部の要素を実行する時、インデックスのない列で検索する時、O(n)になる可能性が高いです。nが無限になるとO(n)も無限になるので、O(n)以上のアルゴリズムはリリース前にリファクタリングする対象です。(何千件以上増えないnは無視して良いです。)
上記以外にも、O(nlogn) (ほとんどのソートのアルゴリズム)、O(n^2) (二重ネスト ループ)、O(2^n)、O(n!) などもありますが、今のところは上記のことだけでも十分です。
計算複雑度を軽減する
ここからが楽しい部分です。計算複雑度をランクダウンさせます。 ご参考になればと思います!
LaravelのEager Loading
Laravelでは一番簡単で認知度が高い問題です。Debugbarで数百件の重複クエリの表示はEager Loadingが効いていない証拠です。load()かwith()を使って修正してください。重複しているけどO(1)に等しい場合はパフォーマンス観点だけで言うと無視して良いです。
インデックス
検索されているカラムにインデックスがない場合はインデックス作ってください。インデックスがあるけど使われない場合は使われるように修正してください。Debugbarからクエリを切り取ってexplainでインデックスが使われているかどうか確認できます。 STR_TO_DATE()やCONCAT()、または %から始まるLIKE式はインデックスが使えない可能性が高いです。
インデックス使われる場合

CONCATによりインデックス使われない場合

また、インデックスが複合インデックスであり、検索されるカラムがインデックスの一番最初のカラムではない場合も、インデックスが使えません。インデックス作成は時間とメモリーのトレードオフであるため、本当に速度の向上が必要かどうか、またカラムが検索の絞り込みに役立つかどうかをよく検討してください (ステータスとかは通常、候補としては不適切です)。
連想配(ディクショナリ、ハッシュマップ)
ソート済み配列のO(logn)よりも検索時間が速いO(1)と言う素晴らしいデータタイプです。例えば、
$collection->where(‘id’, ‘=’, $foo)->first()
をループ内で使うと、最悪の場合の時間がO(n^2)になるので一回
$keyed = $collection->keyBy(‘id’)
でディクショナリを作ってから$keyed->get($foo)で検索した方がO(n)で済ませてパフォーマンスが良いです。
メモ化/キャッシュ (と動的計画法)
時間がかかる計算を何回もしている時はメモ化が有効です。動的計画法と言うメモ化を使って計算複雑度をO(2^n)からO(n)に変更できる魔法の技もありますが現場で適用できる場面があまり見たことないです。代わりに、メモ化でちゃんとボトルネックになっている計算結果を再利用できるように変換して保存しているば結構良いパフォーマンス改善になることはあります。
ページネーション
一覧を返却するAPIには必ずページネーションを入れた方が良いです。時間もメモリーも両方O(n)になる可能性が高いからです。1週間か1ヶ月分のデータしか返却しないAPIでも結構な量になり痛い目あったことありますので全然油断が出来ないです!Laravelのoffsetを使うページネーションはO(n)なので必要であればCursor Paginationの方がおすすめです。
チャンク
メモリーの計算複雑度はあまり触れていませんが、チャンクはその軽減が出来ます。PHPではよく見ることですが、Out of memory (allocated XXXXX) (tried to allocate XXXXX bytes) のエラーが出ると、安易にini_set(‘memory_limit’, 999999999)が使われて使用メモリーが極限まで伸びて最終的にサーバーのアップグレードが必要になる状態…もう見たくないです!チャンク(Laravelの場合$collection->chunk())を使ってください。アップロードファイルが大きすぎる時はブラウザでファイルをチャンクしてからアップロードした方が良いです。
キュー
計算複雑度がどうしても軽減できない場合(データのインポートや出力の時など)、キュー使って一気にO(1)にすることが出来ます。キューでも時間制限ありますのでチャンク使って分けてください。時間がO(n)以上の場合、timeoutがどれぐらい大きく設定しても足りません。チャンクをしないとtimeoutだけではなくLaravelのretry_afterとか、他にどこかの設定も変える必要があり忘れると地獄見ますので。
最後に
ベトナム人で日本語のブログを書いたことがないので日本語のご指摘はウエルカムです!
内容の異論だけは認めません^^