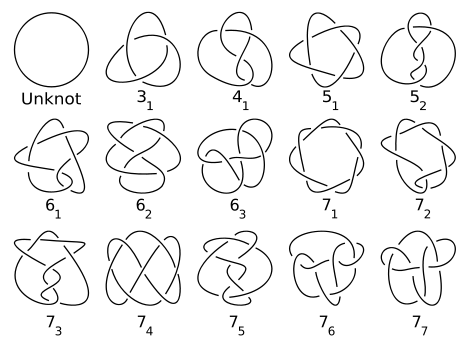
「結び目」について
この記事でいう「結び目」というのは、一つの閉じた円環がどのように絡まっているかを分類したものです。
参照:結び目理論(Wikipedia)
「結び目」に関する文書などを書く際に、簡単に結び目の画像を描くことが出来ないかと考えて、調査してみたことと合わせて記事を書いてみたいと思います。なお、今回の記事は、計算によって曲線を生成する、ということに着目したもので、「結び目理論」とは本質的に関係がありません。
グラフィックツールで描く
手作業で描く手順
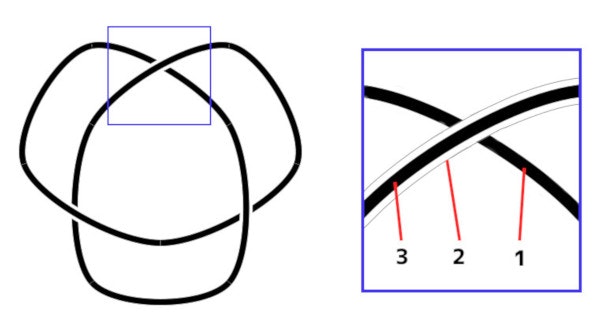
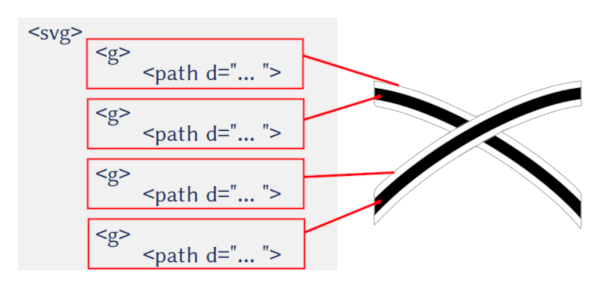
「交叉」している部分以外は、各グラフィックツールで閉曲線を描くことになるので省略します。
「交叉」している部分の描き方は様々な方法があると思いますが、今回は以下のようなやり方で表現しています。
- 下の線を「黒・細いストローク」で描く
- 交叉部分によって下の線を隠すため、上の線を「白・太いストローク」で描く
- 上の線を「黒・細いストローク」で描く
難点
- 曲線を上手に描くのが難しい
多くのグラフィックツールでは曲線を描く場合に、「ベジェ曲線」を使用して編集します。しかし、多数の点を滑らかに通過するような曲線を手作業で描くのは、ツールに慣れていないとなかなか骨が折れる作業です。
- 交叉部分を作るのが面倒
前述した「交叉する部分」の編集は単純ながら、グラフィックツールを使って手作業で行うのはなかなか面倒です。結び目が複雑になってくると、この交叉する箇所が多くなり編集時間や間違いの可能性が増えることが予想されます。
自動的に描くために
今回は、指定した点を通り、SVGを使って滑らかな曲線を表現する調整を計算により求め、また、交叉する部分のSVG編集を同時に行う、ということを目標とします。
入力は、グラフィックツール(Inkscapeを使用)により作成したSVGとして、下記のようなSVG画像を出力します。
基本の3次Bezier曲線
SVGでサポートされている曲線で、簡単な計算式によって様々な形の弧からなる曲線を描くことができます。
[Bézier curves, (Cubic Bézier curves)]
(https://en.wikipedia.org/wiki/Bézier_curve#Cubic_Bézier_curves)
B(t) = (1-t)^3 P_0 + 3(1-t)^2t P_1 + 3(1-t)t^2 P_2 + t^3 P_3 \hspace{10mm} (0 \leq t \leq 1)
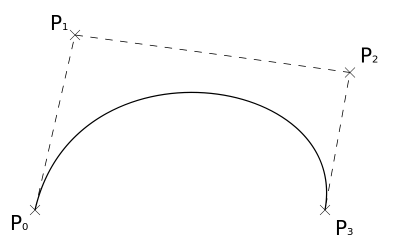
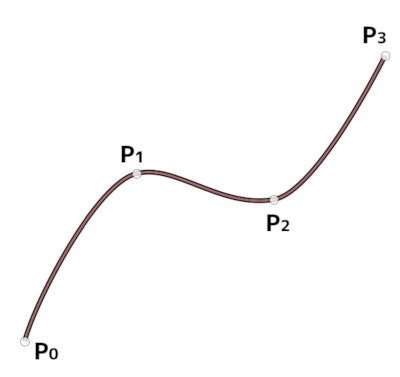
このベジェ曲線の複数の弧を使って、指定した点を通る曲線を生成します。
Catmull-Rom曲線
Bezier曲線を使って、指定した点を滑らかにつなぐには上記の$P_1$、$P_2$を別途計算することが必要になります。今回はCatmull-Rom曲線というものを利用して、Bezier曲線を生成しました。
["Centripetal Catmull–Rom spline" (Wikipedia)]
(https://en.wikipedia.org/wiki/Centripetal_Catmull–Rom_spline)
この曲線はBezier同様に簡単な式で表現できる上に、3次Bezier曲線と相互に変換することが可能です。入力として与えられた点を通るCatmull-Rom曲線をBezier曲線に変換することで、SVGの基本機能のみで描画することが可能になります。
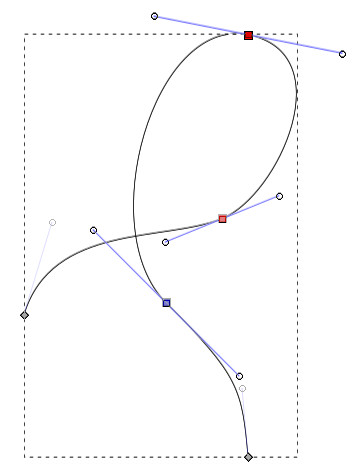
Catmull-RomからBezierへの変換
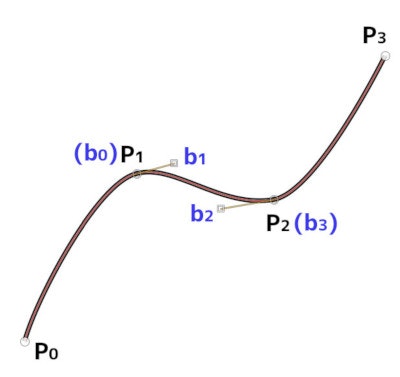
図中、$P_0, P_1, P_2, P_3$ を通るCatmull-Rom曲線の弧 $P_1P_2$ に相当するBezier曲線の点 $b_0, b_1, b_2, b_3$ を求める変換式は、下のようになります。
\begin{align}
b_0 & = P_1 \\
b_1 & = P_1 + \small{\frac{P_2 - P_0}{6}} \\
b_2 & = P_2 - \small{\frac{P_3 - P_1}{6}} \\
b_3 & = P_2
\end{align}
(注) 一般的なCatmull-Rom曲線には曲がり具合を調整するために計算に $\alpha$ という設定値を用いていますが、今回は、簡単のため $\alpha = 0$ として計算しています。
作業、および計算処理の流れ
直線で概形を描く(手作業)
最初に入力するSVGファイルを作成します。ここは手作業です。
このファイルを作る際に、下記の制限を設定しています。
- 制限1:2つの線分が交叉する場合は端点以外の場所で交叉する
- 制限2:全体として1個の閉じた曲線を構成する
作成した曲線(線分で構成された閉曲線)をSVGファイルとして保存し、プログラムの入力とします。
SVGファイルを読み込み、path要素内のd属性を見つける
以下、node.jsを使用して作成したものについて説明します。
上記のSVGドキュメント内に存在するpath要素のd属性を読み込みます。
ここでは、jsdomを利用してSVGをDOMとして扱っています。
const fs = require("fs");
const jsdom = require('jsdom');
const { JSDOM } = jsdom;
fs.readFile(process.argv[2], 'utf8', function(error, data) {
// obtain svg path string
const dom = new JSDOM(data);
const path_d = dom.window.document
.querySelector("svg path")
.getAttribute("d");
path要素のd属性を解析して頂点を求める
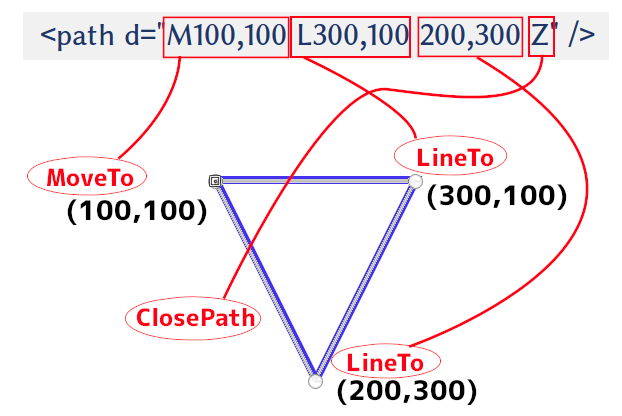
path要素のd属性には、SVGの描画命令文が格納されています。命令文を解析して座標を計算し、頂点として必要なものを抽出します。
今回は、MoveTo命令とLineTo命令のみを読み取れば良いので、ごく簡単な解析で済ませています。
// parse path string to get end points
let pathSentence = path_d.match(/[mzlhvcsqta][0-9\-., ]*/gi)
for (let phrase of pathSentence) {
let cmd = phrase[0];
if (cmd === "m" || cmd === "l") {
// move and lineTo
let points = phrase.slice(1)
.trim()
.split(/[\s,]+/)
let x = points.shift();
let y = points.shift();
//... (以下略、必要であれば後述のソースコードを参照してください)
交叉する弧を見つける
全ての2つの線分の組み合わせについて、「交叉するか否か」を判断し、その情報から配列を生成します。後の工程で曲線の弧が「上を通る」か「下を通る」かを切り替える場所となります。
なお、「入力の線分が交叉するなら、生成するCatmull-Rom曲線の弧が交叉する」、また「線分が交叉しないなら、弧は交叉しない」という前提です(その前提が成立するように入力用SVGファイルを作成する必要があります)。
function isCrossing(segments0, segments1) {
let [p0, p1] = segments0;
let [p2, p3] = segments1;
let [x0, y0] = p0;
let [x1, y1] = p1;
let [x2, y2] = p2;
let [x3, y3] = p3;
// bounding boxes test
let b = Math.max(x0, x1) > Math.min(x2, x3) &&
Math.min(x0, x1) < Math.max(x2, x3) &&
Math.max(y0, y1) > Math.min(y2, y3) &&
Math.min(y0, y1) < Math.max(y2, y3);
if (b) {
// cross product test
let cp0 = (x2 - x0) * (y3 - y0) - (y2 - y0) * (x3 - x0);
let cp1 = (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1);
let cp2 = (x0 - x2) * (y1 - y2) - (y0 - y2) * (x1 - x2);
let cp3 = (x0 - x3) * (y1 - y3) - (y0 - y3) * (x1 - x3);
return (cp0 * cp1 < 0) && (cp2 * cp3 < 0);
}
return false;
}
Catmull-Rom曲線をSVGのBezierで描く
前述の変換式を使って、Catmull-Rom曲線を生成するBezire曲線の各点を求めます。
//
// convert Catmull-Rom endpoints to cubic Bezier nodes
//
function catmullRomToBezier(endPoints) {
let bezierNode = [];
bezierNode.push(endPoints[0]);
endPoints.forEach((p, i, a) => {
let P0 = a[(i - 1 + a.length) % a.length]
let P1 = p
let P2 = a[(i + 1) % a.length]
let P3 = a[(i + 2) % a.length]
// Catmull-Rom to Bezier conversion (alpha=0)
let Cb1x = P1[0] + (P2[0] - P0[0]) / 6
let Cb1y = P1[1] + (P2[1] - P0[1]) / 6
let Cb2x = P2[0] - (P3[0] - P1[0]) / 6
let Cb2y = P2[1] - (P3[1] - P1[1]) / 6
// push cubic bezier points
bezierNode.push([Cb1x, Cb1y])
bezierNode.push([Cb2x, Cb2y])
bezierNode.push(P2)
});
return bezierNode;
}
交叉部分を作る
生成されたCatumull-Rom曲線(SVG内ではBezier曲線で表現)の弧で交叉する部分を作ります。
g要素をレイヤーとして用いることによって、基本的には手作業で作成したのと同じ表現方法です。
出力
jsdomのDOMを利用して全体をSVGドキュメントとして完成し、最終的にテキストとして出力して終了です。
//
// create simple svg document with a Catmull-Rom curve
//
function draw_svg(endPoints, crossing, viewBox) {
// create document root and body
const document = new JSDOM().window.document;
const body = document.body;
// create svg element
const svgns = "http://www.w3.org/2000/svg";
const svg = document.createElementNS(svgns, "svg");
// ... (中略)
// construct svg document and output as text
body.appendChild(svg);
return document.body.innerHTML;
}
完成したもの
以上を、コマンドラインから使用できるプログラムとして作成したものをGitHub上にまとめました。
node draw_knot.js input.svg > output.svg
生成したSVGドキュメントは標準出力に表示されます。
なお、今のところ、Inkscapeで作成したSVGでのみ動作を確認しています。今回の記事の内容のデモンストレーションが目的であって、あまり汎用的なツールとなることを目的とはしておりません。動作不良などは悪しからずご了承ください。
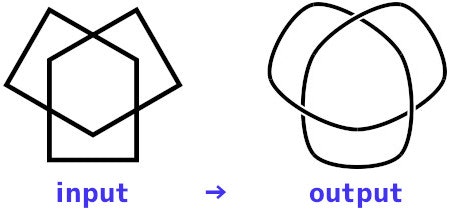
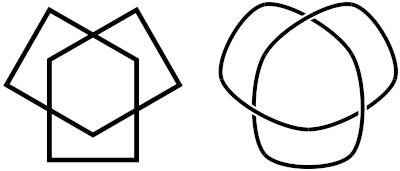
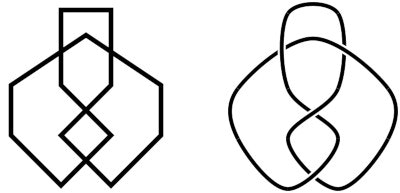
作図例(入力と出力)
まとめ
今回の調査の元々のきっかけは、様々なデータを可視化する際に、matplotlibやd3.jsを使ってカスタマイズした図を作るよりも、SVGなどの基本的な機能で描画したほうが手っ取り早く、見やすいものができるのではないか、という考えからSVGの基本機能を調査してみよう、というものでした。
簡素ではあるけれども、「特殊な用途のための図」にぴったりのものがない場合に、ひとつの選択肢として考慮してみるのも良いと思います。
参考にした記事など
[Centripetal Catmull–Rom spline]
(https://en.wikipedia.org/wiki/Centripetal_Catmull–Rom_spline)
[Bézier curves, (Cubic Bézier curves)]
(https://en.wikipedia.org/wiki/Bézier_curve#Cubic_Bézier_curves)
[A Primer on Bézier Curves: 34. Bézier curves and Catmull-Rom curves]
(https://pomax.github.io/bezierinfo/#catmullconv)