昭和以降の全横綱データをスクレイプしてサバイバル分析にかけたら、突っ張り横綱は短命なのがわかった。
Photo By Better Than Bacon CC BY 2.0
現在、日馬富士による暴行事件で相撲界は賑わっていますが、その中でもそうした騒動の問題を起こす中心に横綱がいるというのは誠に残念と言わざるを得ません。そんな中、先の場所で白鵬が優勝しました。彼は実はすでに40回も優勝していて、さらに横綱歴が10年らしいです。結構長い間横綱なんだなというかんじですが、そもそも今までの横綱というのは、普通どれくらいの間横綱でいつづけるのでしょうか?横綱の時期の一番長い、もしくは一番短い力士は誰なのでしょうか?さらに、横綱の時期の長い力士というのは、短い力士に比べて何か特徴があるのでしょうか?例えば、モンゴルなど外国人力士というのは日本人力士に比べて長いのでしょうか、それとも短いのでしょうか?
今日はこういった質問に答えるべくデータサイエンスの手法を使って分析をしてみたいと思います。方針としては、
- 横綱のデータをウェブ・スクレイピングして取ってくる。
- 可視化して簡単な質問に答える。
- サバイバル分析のアルゴリズムを使って、出身地別、体重別などのコホートごとの横綱引退率を分析する。
という感じで行います。今回もプログラミングなしでデータサイエンスができるツールであるExploratoryを使ってさくっと行ってみたいと思います。
データの取得
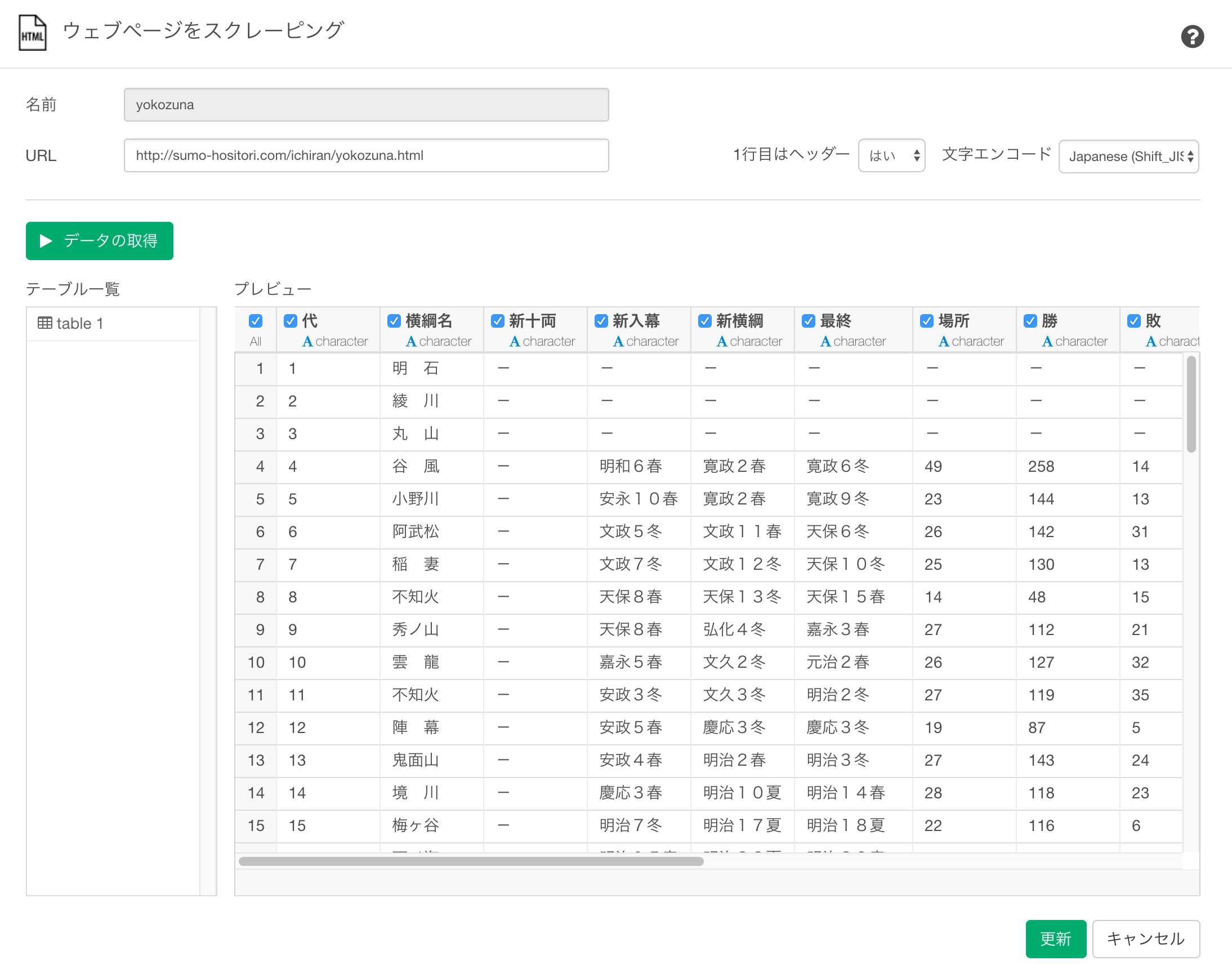
ありがたいことに、大相撲星取表に第4代横綱の谷風から第72代横綱の稀勢の里までの勝率や、横綱に昇進した年、引退した年のデータがまとめられています。さらにそれぞれの力士の出身地、身長、体重、得意技等の補足情報はWikipediaのそれぞれの力士のページにあります。ということで、これらをスクレイピングしてデータを揃えることができます。大相撲星取表のサイトはウェブページをスクレーピングのダイアログでURLを入れると取れます。
Wikipediaのサイトは作りが複雑なので、横綱の追加情報をスクレイピングするのに、ちょっとしたRのスクリプトを書いて、それをExploratoryから呼び出すとロードできます。
get_wiki_rikishi <- function(name) {
url <- paste0("https://ja.wikipedia.org/wiki/",name)
html <- read_html(url)
tb1 <- html %>% html_node("table") %>% html_table(header = FALSE, fill=TRUE)
tb2 <- tb1 %>% spread(X1, X2)
tb2
}
yokozuna_df <- data.frame(X1=character(0))
for (name in names_df$name[c(1:17, 19:39, 42, 44:54, 56:63,65,68:72)]) {
tryCatch({
df0 <- get_wiki_rikishi(name)
yokozuna_df <- yokozuna_df %>% bind_rows(df0)
}, error = {
cat(name)
})
}
可視化して簡単な質問に答える
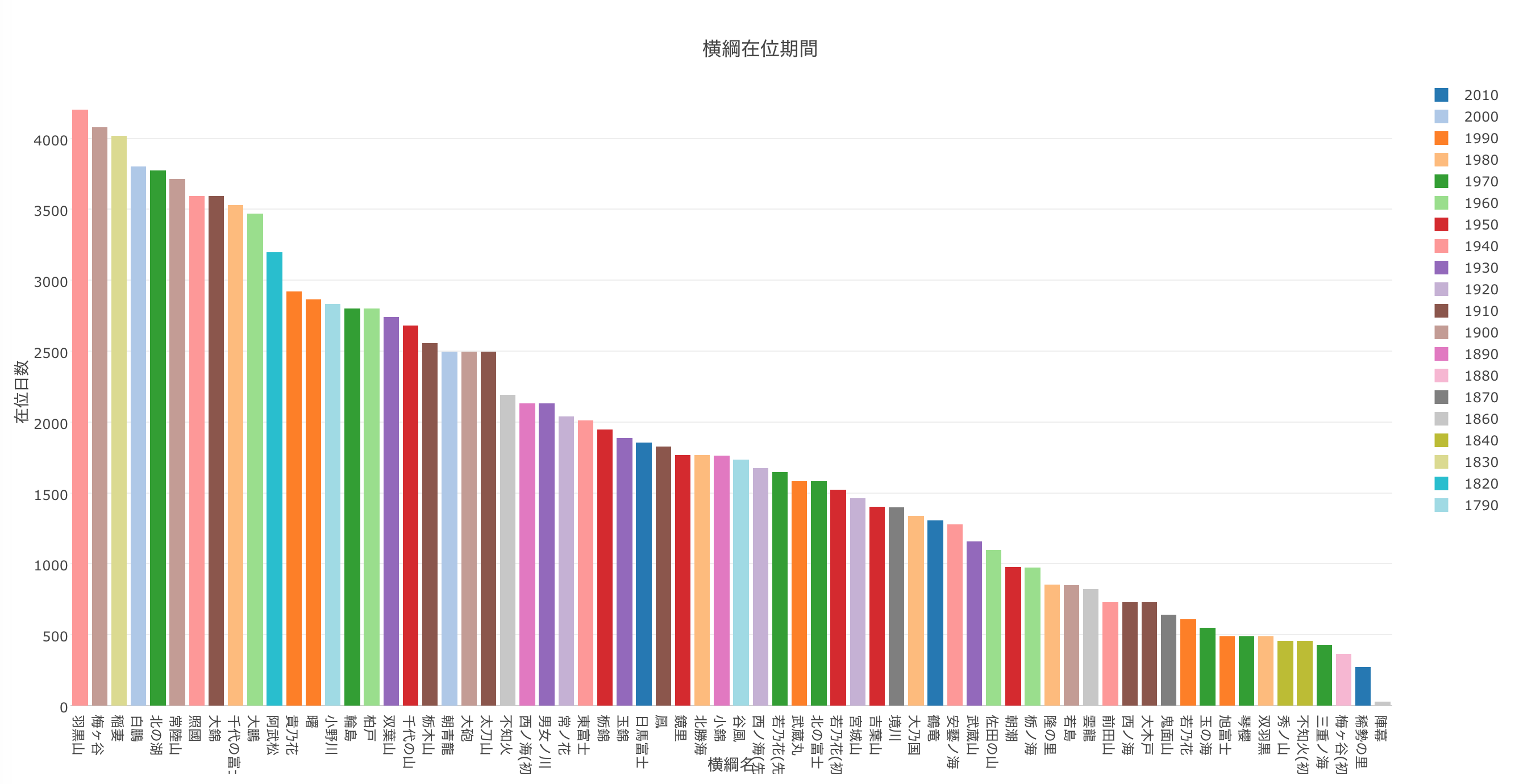
まずは、歴代の横綱の在位日数をバーグラフで表すと以下のようになります。色は「横綱に昇進した年」を10年毎に分けた年代となっています。
まず一番右側の在位期間が一番短い力士ですが、他と比べてとても短いのに気づきます。明治維新の頃の力士で陣幕、たった1ヶ月となっています。
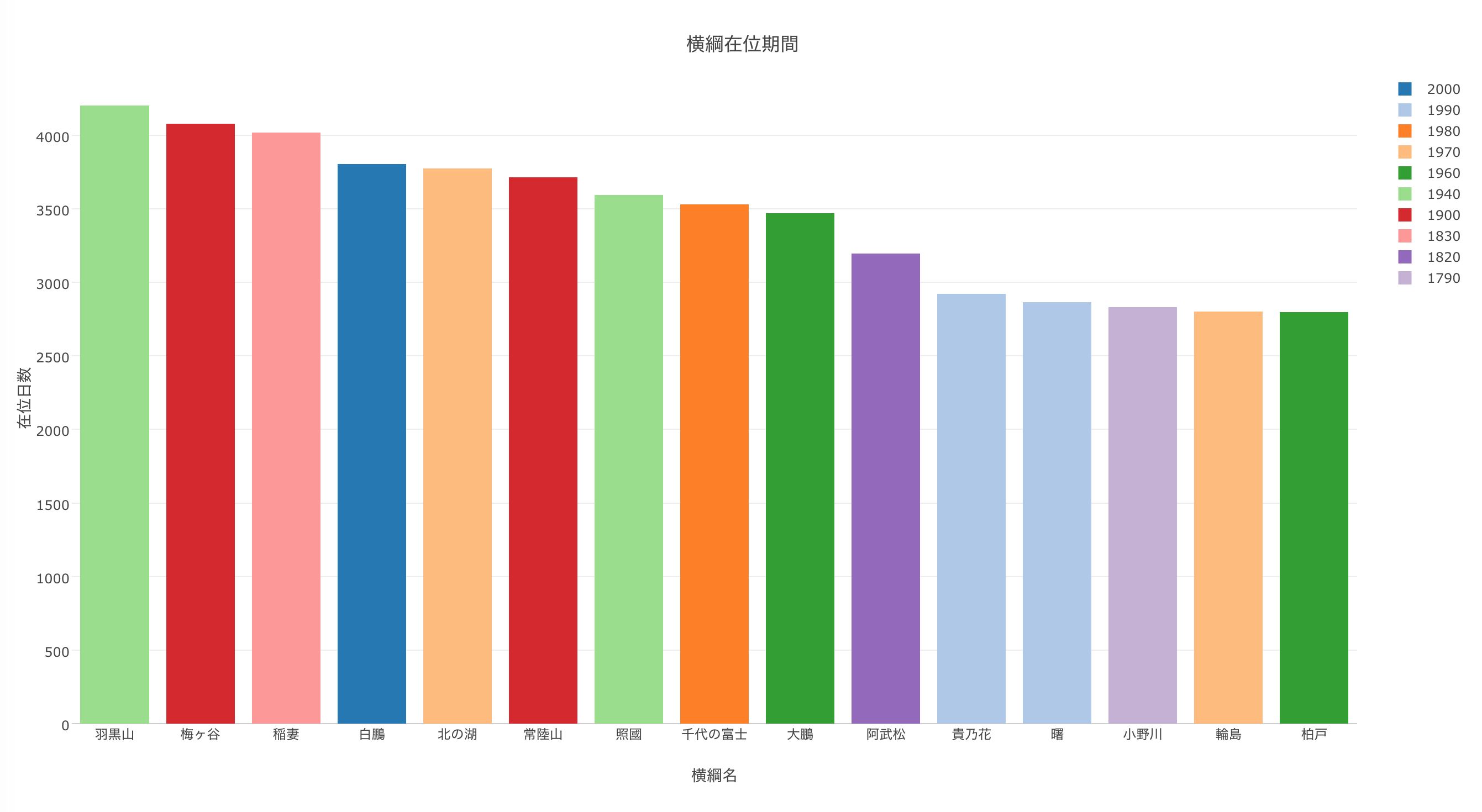
では、上位を確認しますが、上のチャートは若干混み合っているので、横綱在位日数のトップ15の横綱にして見ましょう。
左から4番目の青のバーが白鵬ですが、歴代4位の長さなんですね。ちなみに、一番長いのは1940年代に活躍した羽黒山で4202日でなんと11年6ヶ月です。
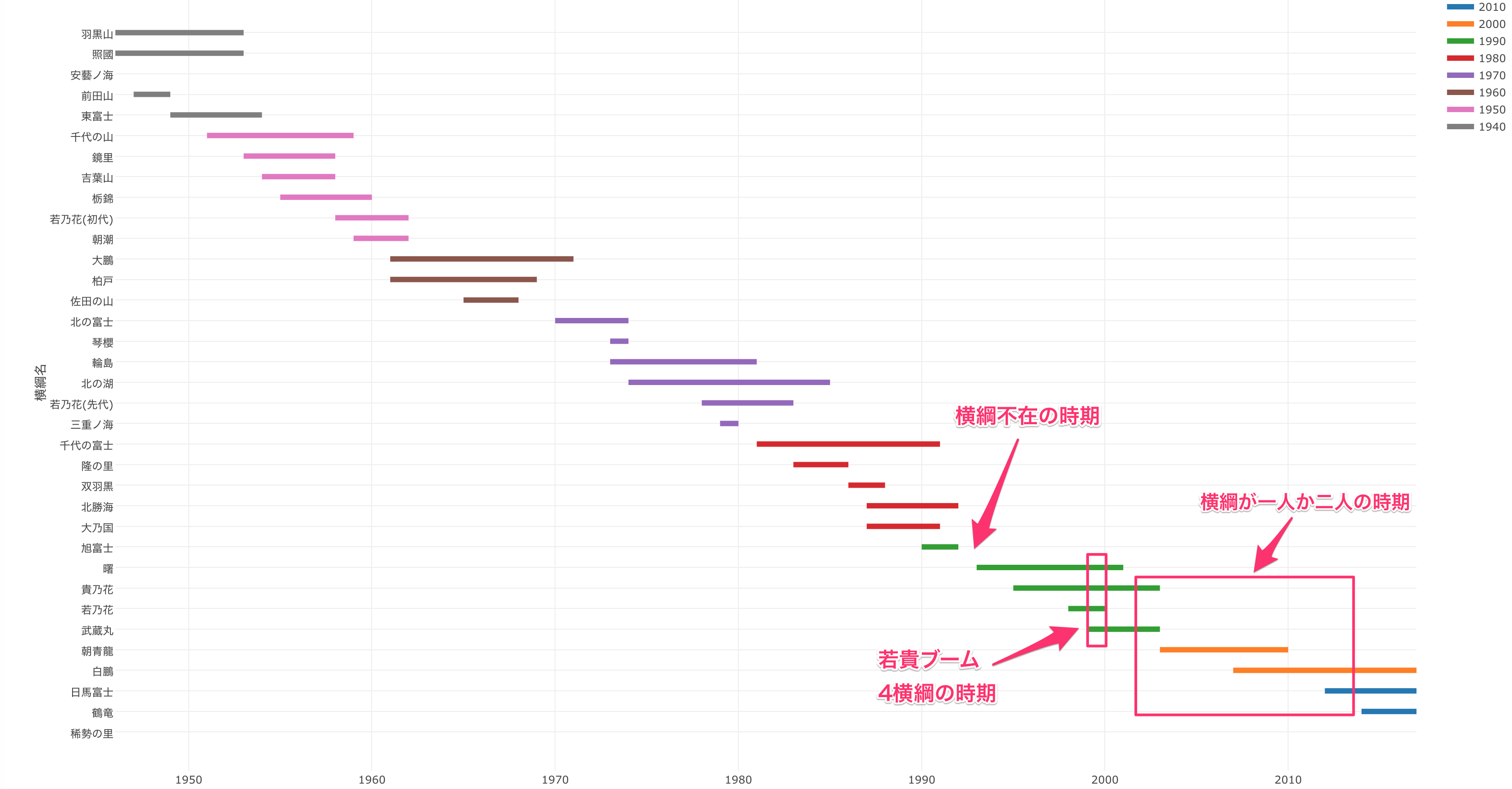
戦後(1945年以降)にどの力士が、どの時代にどれだけの期間横綱の座にいたのかを、以下のチャートで、それぞれの力士の在位期間を横軸にとって表してみました。
これを見ると、たいていの時代では二人か三人の横綱が同時にいますが、多い時は千代の富士が活躍した1980年代(赤)、若貴ブームの1990年代(緑)、現在の白鵬、日馬富士、鶴竜、稀勢の里の時代のように四人同時にいる時もあります。と思っていたら、昨日、日馬富士が引退のニュースが入ってきましたので、また3人に戻ってしまいますね。
ところで、90年代に旭富士が引退した後、曙が横綱になるまでの間、横綱不在の時期があったのですね。
コホートごとに昭和以降の横綱引退率を分析する
それでは、ここからが今日のメインの分析です。最初に述べたように、私が知りたいのは、横綱在位期間が長い/短い、つまりは 長寿の横綱と、そうでない横綱との違いは何なのかということです。例えば、モンゴルなど外国人力士というのは日本人力士に比べて現役続行する傾向にあるのか、体重の重い横綱は軽い横綱に比べて引退しやすいのか、または得意技によって違いがあるのかということです。
実はこうした分析はサバイバル分析系のKaplan-Meier というアルゴリズムを使って比較的簡単に行うことができます。このアルゴリズムはデータサイエンスの世界ではよく顧客の離脱率、従業員の離職率、製品の故障率、がん患者の死亡率など、時間が経てば経つほどそうした確率が高まっていくものの分析に使われます。
今回私の興味のある横綱の引退までの長さも、横綱になってから何日目にどれくらいの割合の横綱が引退しているのかという、いわゆる引退率という見方をすることで、同じ手法を使うことができます。ちなみに、このサバイバル分析系のKaplan-Meier というアルゴリズムの詳細についてはこちらに簡単な紹介ビデオがあるので、興味のある方は見てみて下さい。
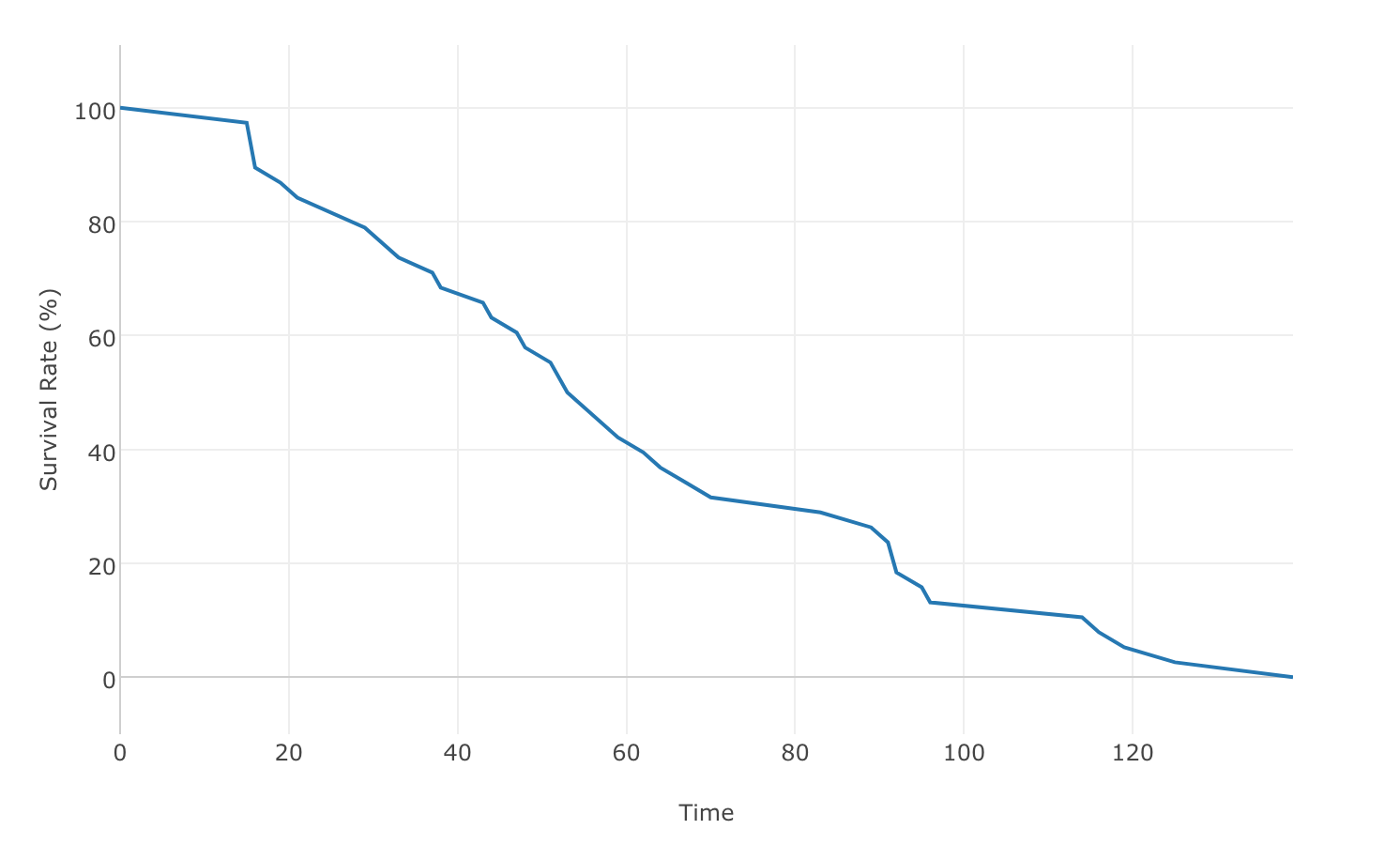
まずは、昭和以降に横綱になった力士の引退率を見てみましょう。
X軸が横綱に昇進してからの期間(単位は月)、Y軸が生存率、つまりどれくらの割合の横綱が引退しないで現役でいる率を示しています。この線の傾き - カーブ - が急な期間ではそこで引退していく率が高いと言えます。
それでは、このカーブをそれぞれのコホートに分けることで、それぞれのコホートを比べてみましょう。
(注意:まだ現役の横綱はここでは除外しています。)
体重区分毎の分析
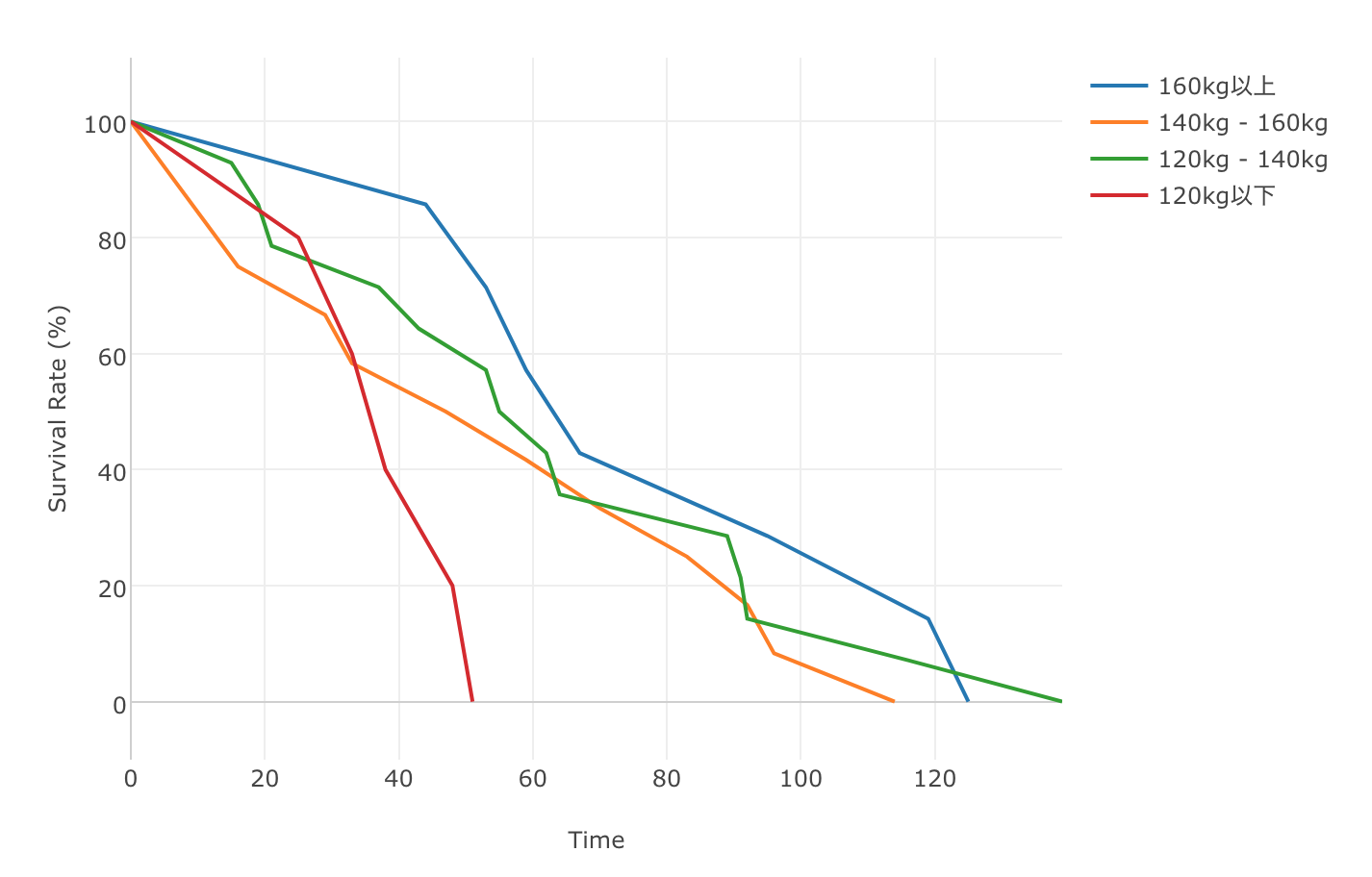
次に、体重を以下のように分けたコホートを作り「色」に割り当ててみます。
- 160kg以上
- 140kg - 160kg
- 120kg - 140kg
- 120kg以下
すると、体重が重いコホートが軽いコホートに比べて、カーブが緩やかになっていくのがみてとれます。つまり在位率が比較的高いということです。ところで、特に120kg以下である赤いカーブの傾きが急ですが、このコホートには武蔵山、若乃花(初代)といった横綱がいます。
それぞれのコホートに属する横綱は以下の通りです。
| カテゴリ | 横綱名 | 体重 |
|---|---|---|
| 160kg以上 | 北の湖 | 169 |
| 大乃国 | 203 | |
| 曙 | 233 | |
| 東富士 | 178 | |
| 武蔵丸 | 235 | |
| 照國 | 162 | |
| 鏡里 | 165 | |
| 140kg - 160kg | 北勝海 | 150 |
| 双羽黒 | 157 | |
| 吉葉山 | 143 | |
| 大鵬 | 153 | |
| 旭富士 | 143 | |
| 朝潮 | 145 | |
| 朝青龍 | 154 | |
| 柏戸 | 143 | |
| 琴櫻 | 150 | |
| 男女ノ川 | 146 | |
| 貴乃花 | 150 | |
| 隆の里 | 158.50 | |
| 120kg - 140kg | 三重ノ海 | 135 |
| 佐田の山 | 129 | |
| 北の富士 | 135 | |
| 千代の富士 | 126 | |
| 千代の山 | 122 | |
| 双葉山 | 135 | |
| 安藝ノ海 | 128 | |
| 栃錦 | 132 | |
| 玉の海 | 135 | |
| 玉錦 | 136 | |
| 羽黒山 | 130 | |
| 若乃花 | 134 | |
| 若乃花(先代) | 133 | |
| 輪島 | 132 | |
| 120kg以下 | 前田山 | 120 |
| 宮城山 | 113 | |
| 栃ノ海 | 110 | |
| 武蔵山 | 116 | |
| 若乃花(初代) | 107 |
出身地域毎の分析
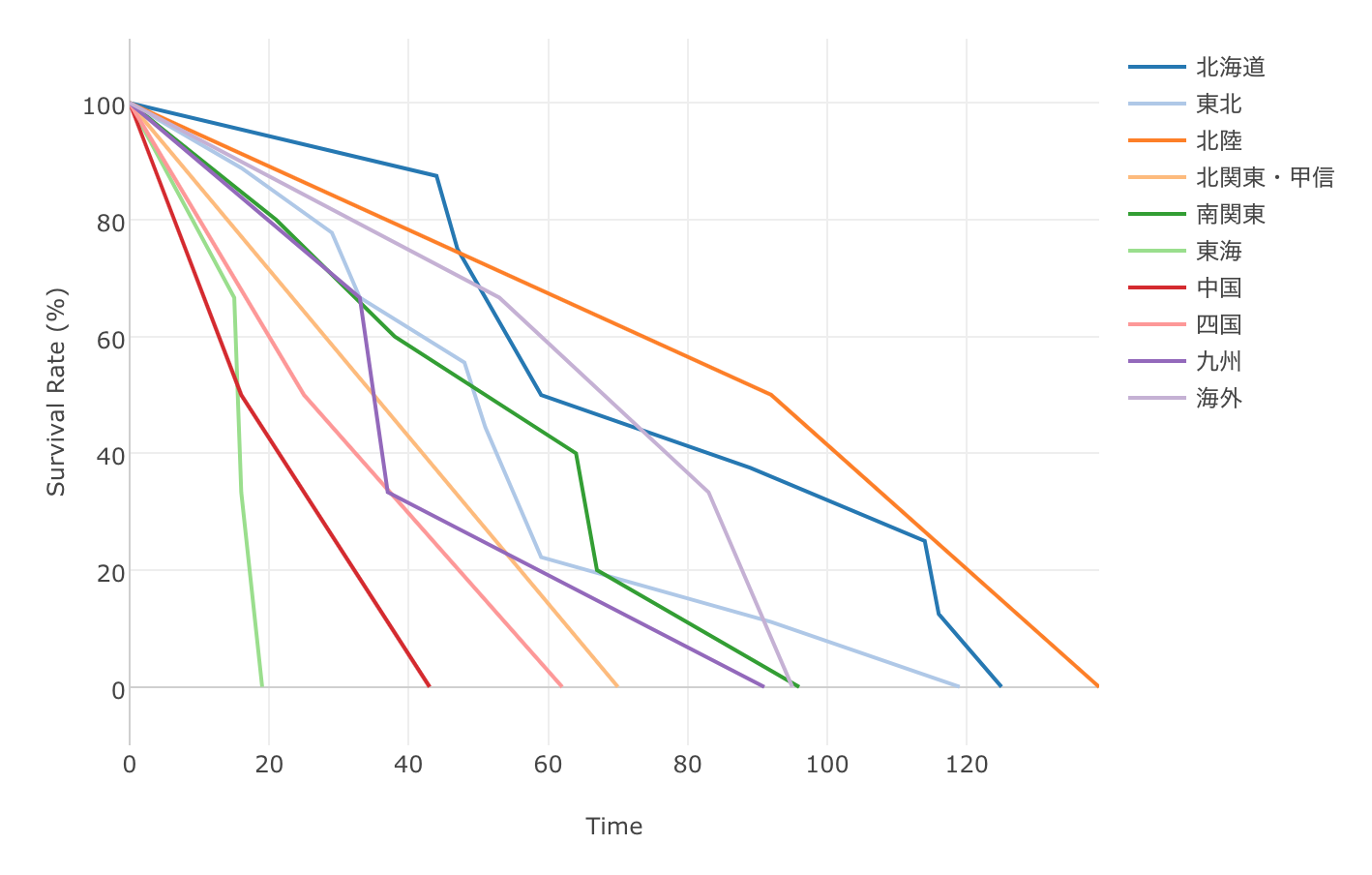
今度は地域に注目してみましょう。「色」に出身地域を割り当てると、出身地域毎の比較がしやすくなります。
これをみると北陸(オレンジの線)、北海道(濃い青の線)といった日本の北側、さらにモンゴル、ハワイなどの海外出身(薄い紫の線)の横綱は、他の地域と比べて在位期間が長く、引退していく割合も緩やかなのが分かります。逆に東海地方(薄い緑の線)と、中国地方(赤い線)出身の横綱は引退する率が急で、在位期間も短いことが分かります。
それぞれのコホートに属する横綱は以下の通りです。
| 地域 | 横綱名 | 都道府県 |
|---|---|---|
| 北海道 | 北の富士 | 北海道 |
| 北の湖 | 北海道 | |
| 北勝海 | 北海道 | |
| 千代の富士 | 北海道 | |
| 千代の山 | 北海道 | |
| 吉葉山 | 北海道 | |
| 大乃国 | 北海道 | |
| 大鵬 | 北海道 | |
| 東北 | 宮城山 | 岩手 |
| 旭富士 | 青森 | |
| 柏戸 | 山形 | |
| 栃ノ海 | 青森 | |
| 照國 | 秋田 | |
| 若乃花(先代) | 青森 | |
| 若乃花(初代) | 青森 | |
| 鏡里 | 青森 | |
| 隆の里 | 青森 | |
| 北陸 | 羽黒山 | 新潟 |
| 輪島 | 石川 | |
| 北関東・甲信 | 男女ノ川 | 茨城 |
| 南関東 | 東富士 | 東京 |
| 栃錦 | 東京 | |
| 武蔵山 | 神奈川 | |
| 若乃花 | 東京 | |
| 貴乃花 | 東京 | |
| 東海 | 三重ノ海 | 三重 |
| 双羽黒 | 三重 | |
| 玉の海 | 愛知 | |
| 中国 | 安藝ノ海 | 広島 |
| 琴櫻 | 鳥取 | |
| 四国 | 前田山 | 愛媛 |
| 玉錦 | 高知 | |
| 九州 | 佐田の山 | 長崎 |
| 双葉山 | 大分 | |
| 朝潮 | 鹿児島 | |
| 海外 | 曙 | 米 |
| 朝青龍 | モンゴル | |
| 武蔵丸 | 米 |
得意技毎の分析
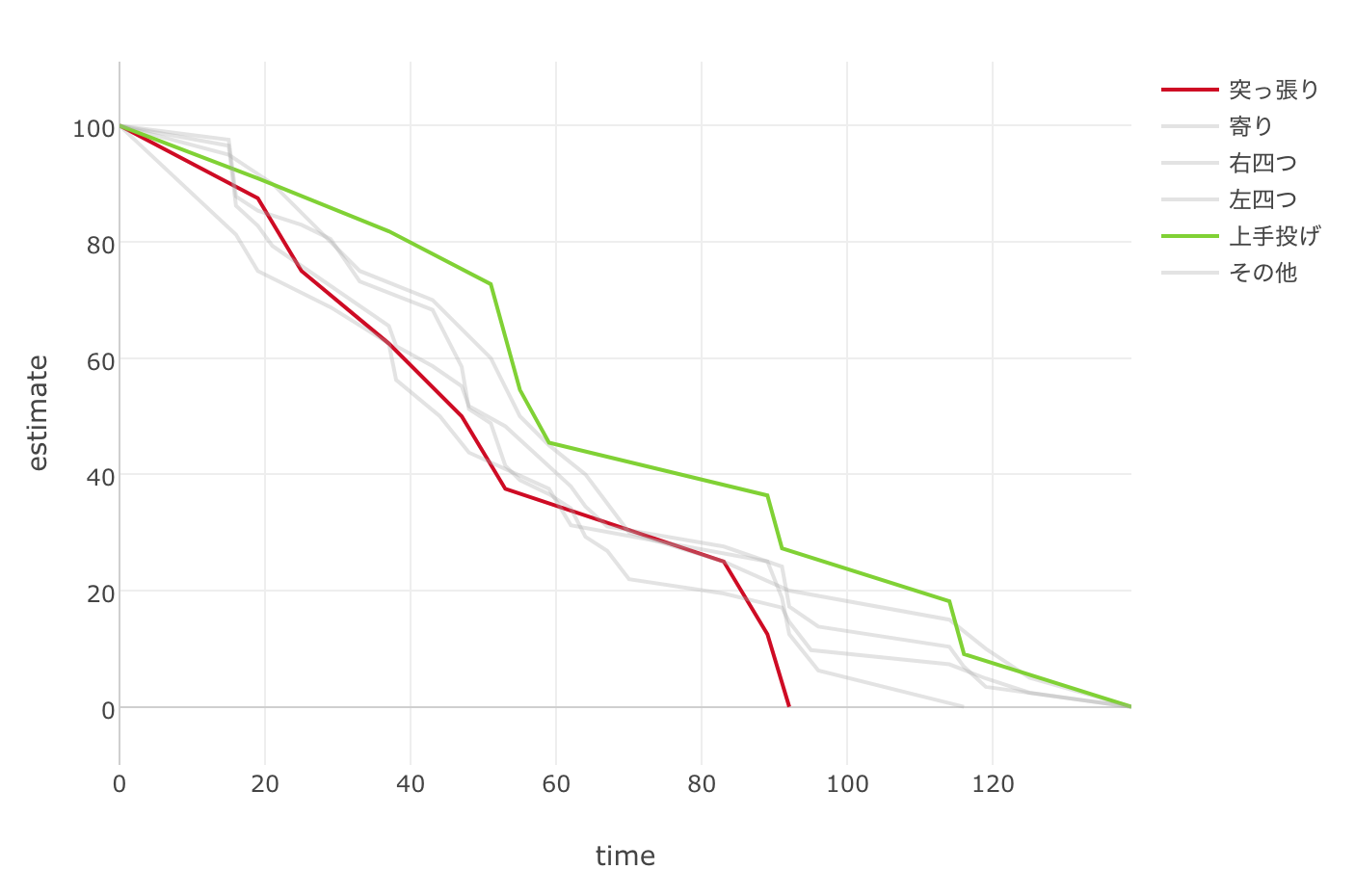
最後に、力士の得意技をもとにしたコホートを作って比べて見ましょう。
突っ張りを得意技とする力士のコホートの在位率の下落カーブが80ヶ月を超えたあたりで急激に下がるのがわかります。やはり、突っ張りというのは打撃系の勝負を挑むということなので勝とうが負けようが消耗が激しく、それによるダメージが蓄積されていくということでしょうか?
逆に、上手投げを得意技とする力士のコホートのカーブが他と比べて緩やかで、引退しにくいということが見て取れます。
ちなみに、ここでのインサイトは相関関係であり、原因ではありません。つまりそうした相関関係から私なりにその原因を推測しているということなので、横綱が急に突っ張りをやめたからといってそれで横綱在位期間が長くなるということでありませんので、もしこれをたまたま読んでいる力士の方がいたら、今後もどんどん突っ張っていって下さい。(笑)
ちなみに、突っ張りを得意としていた横綱といいますと、以下の面々です。
| 横綱名 |勝率 | 得意技 | 在位日数|在位期間ランク|
|----|----------|---------|---------|-------|--------|
| 柏戸 |0.714 |突っ張り |2799 | 24|
| 千代の山 |0.711 |突っ張り |2679 | 31|
| 朝青龍 |0.796 |突っ張り |2498 | 34|
| 北の富士 |0.668 |突っ張り |1583 | 62|
| 吉葉山 |0.668 |突っ張り |1402 | 75|
| 佐田の山 |0.726 |突っ張り |1096 | 89|
| 前田山 |0.665 |突っ張り |731 | 102|
| 玉の海 |0.68 |突っ張り |549 | 108|
まとめ
今日はWebスクレイピングして来た横綱のデータを使って、横綱の在位期間を生存分析のアルゴリズムを使って簡単にコホート分析してみました。横綱というのはそもそもそんなに数がいるわけではなく、ここで得られたインサイトは統計的な検証に耐えれるという保証はありません。しかしこうしてデータサイエンスのアルゴリズムを分析の初期のステップである探索的なデータ分析の段階でどんどん使っていくことで、効率的に大まかなトレンド、または隠されたパターンをすばやくつかんでいくことができます。
まだExploratory Desktopをお持ちでない場合は、こちらから30日間無料でお試しいただけます。
データサイエンスを本格的に学んでみたいという方へ
来年1月の中旬に、Exploratory社がシリコンバレーで行っているトレーニングプログラムを日本向けにした、データサイエンス・ブートキャンプが東京で行われます。データサイエンスの手法を基礎から体系的に、プログラミングなしで学んでみたい方、そういった手法を日々のビジネスに活かしてみたい方はぜひこの機会に、参加を検討してみてください。