高校数学の範囲のtan の逆関数については
公式的なものが数多くありますな
プログラマーの方ならマーチンの公式がすぐに思いつくかと思いますが
世の中一般的には
試験にも多く出題されている一番有名な式は以下ではないでしょうか?
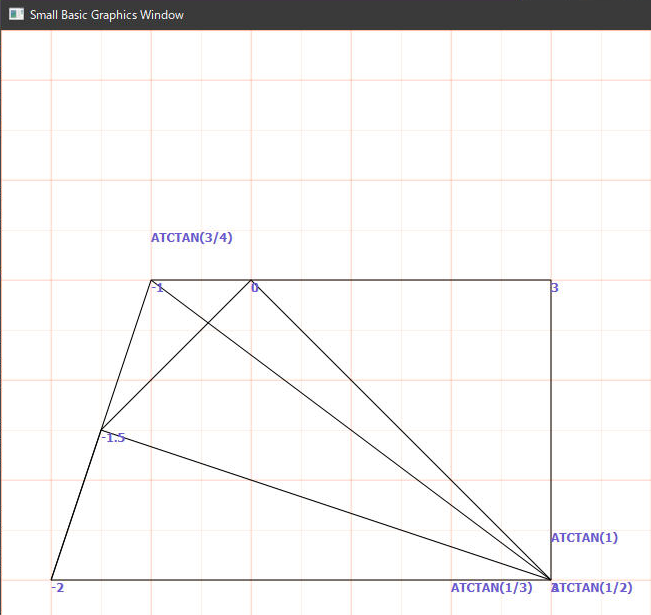
arctan(1/1)+arctan(1/2)+arctan(1/3)=π/2
もしくは
arctan(1/2)+arctan(1/3)=π/4
私は上の式のほうが美しさを感じますな
加法定理や倍角の公式を使って
数式変形でがしがし解くのは
つまらないし
式の美しさをまったく無視していると思いますな
上の式については
作図のみでの解法も
かなり有名でございますな
公式のシンプルさ、美しさと
その式の持つ意味を直接
解き明かして示しているのが
作図のみで解法ではないかと思いますな
というわけで・・・・
上の式の解法を作図してみたいわけですが
Small Basicで作成してみましたよ
数学などの学習を本願とする方々は
プログラム言語にまで時間をかけて習得することが
困難ではないかと思いますんで
初心者向けの専門知識がなくても
実行や理解ができるものが望まれますな
Scratch が有名ですが
自分の子供はもう中学生で
あういう子供っぽい雰囲気には
興味を示さないようになってますので・・・
ソースコードと実行は
こちらからどうそ
Program Listing - Microsoft Small Basic Online
Small Basic はソースコードが簡単に共有できる上に
最新版のSmall Basicなら
どのブラウザ経由でもそこそこちゃんと動いてくれるんで便利ですな
Small Basic Online のプレビュー版は期待させる内容でしたが
正式版は期待を裏切る内容でしたよ
もう更新もないようですしSmall Basicはオワコンかもしれませんな
子供向のプログラム言語でもう1つ
プチコン (smile basic)も同じく共有できますので
時間があればプチコン版も作成してみたいですな
Main()
Program.End()
'----------------------------------------------------
Sub plot
'ATCTAN(1)
L1=Shapes.AddLine(M0,M0,M6,M0)'(0,0)- (6,0) →
d50()'delay 500 msec
Shapes.AddLine(M6,M0,M6,M6)'(6,0)- (6,6) ↓
d50()
Shapes.AddLine(M6,M6,M0,M0)'(6,6)- (0,0)↖
d100()
Shapes.Move(Shapes.AddText(0),M0,M0)
Shapes.Move(Shapes.AddText(3),M6,M0)
Shapes.Move(Shapes.AddText(3),M6,M6)
Shapes.Move(Shapes.AddText("ATCTAN(1)"),M6,M5)
d100()
'ATCTAN(1/2)
Shapes.AddLine(M0,M0,MM3,M3)'(0,0)- (-3,3) '↙
d50()
Shapes.AddLine(MM3,M3,M6,M6)'(3,3)- (6,6)'↘
Shapes.Move(Shapes.AddText(-1.5),MM3,M3)
Shapes.Move(Shapes.AddText("ATCTAN(1/2)"),M6,M6)
d100()
'ATCTAN(1/3)
Shapes.AddLine(MM3,M3,MM4,M6)'(-3,3)- (-4,6)
d50()
Shapes.AddLine(MM4,M6,M6,M6)'(-4,6)- (6,6)
Shapes.Move(Shapes.AddText(-2),MM4,M6)
Shapes.Move(Shapes.AddText("ATCTAN(1/3)"),M4,M6)
d100()
'ATCTAN(3/4)
Shapes.AddLine(MM4,M6,MM2,M0)'(-4,6)- (-2,0)'↗
d50()
Shapes.AddLine(M0,M0,MM2,M0)'(0,0)- (-2,0)'←
d50()
Shapes.AddLine(MM2,M0,M6,M6)'(-4,6)- (6,6)
d50()
Shapes.Move(Shapes.AddText(-1),MM2,M0)
Shapes.Move(Shapes.AddText("ATCTAN(3/4)"),MM2,MM1)
d100()
d100()
EndSub
Sub TextWrite
TextWindow.Top=0
TextWindow.Left=M8
TextWindow.WriteLine("arctan(1/1)+arctan(1/2)+arctan(1/3)=π/2")
TextWindow.WriteLine("arctan(4/3)+2arctan(1/3)=π/2")
TextWindow.WriteLine("hypotenuse of right triangle(3 and 4 ) = 5")
EndSub
'----------------------------------------------------
Sub Main
INIT_CONST()
TextWrite()
'10 time repeat
repeat=10
isFirst=true
While(repeat>=0)
INIT_GraphicsWindow()
MakeHouganshi()
j=200+ (repeat-5)*(repeat-5)/2
R=j * Math.Remainder( Math.Remainder(repeat+2,5),2)
B=j * Math.Remainder(Math.Remainder(repeat,3),2)
G=j * Math.Remainder(Math.Remainder(repeat+1,3),2)
GraphicsWindow.PenColor= GraphicsWindow.GetColorFromRGB(R,B,G )
plot()
repeat=repeat-1
isFirst=false
EndWhile
EndSub
'----------------------------------------------------
Sub INIT_GraphicsWindow
'GraphicsWindow.top=0
'GraphicsWindow.Left=0
GraphicsWindow.Clear()
GraphicsWindow.Height=M12
GraphicsWindow.Width=M12
EndSub
'----------------------------------------------------
Sub MakeHouganshi
maxidth=1800
GraphicsWindow.PenColor="Coral"
For y=0 To maxidth Step M
GraphicsWindow.DrawLine(0,y,maxidth,y)
GraphicsWindow.DrawLine(y,maxidth,y,0)
If Math.Remainder(y/M,2)=0 Then
GraphicsWindow.PenWidth=0.4
Else
GraphicsWindow.PenWidth=0.063
EndIf
EndFor
GraphicsWindow.PenColor="blue"
GraphicsWindow.PenWidth=1
EndSub
Sub d50
Program.Delay(500)
EndSub
Sub d100
Program.Delay(1000)
EndSub
'----------------------------------------------------
Sub INIT_CONST
true=-1
false=0
M=50
OX=5M
OY=5M
M0=OX
M1=1M+OX
M2=2M+OX
M3=3M+OX
M4=4M+OX
M5=5M+OX
M6=6M+OX
M7=7M+OX
M8=8M+OX
M9=9M+OX
M10=10M+OX
M11=11M+OX
M12=12M+OX
'minus number
MM1=-1M+OX
MM2=-2M+OX
MM3=-3M+OX
MM4=-4M+OX
MM5=-5M+OX
MM6=-6M+OX
MM7=-7M+OX
MM8=-8M+OX
MM9=-9M+OX
MM10=-10M+OX
MM11=-11M+OX
MM12=-12M+OX
EndSub