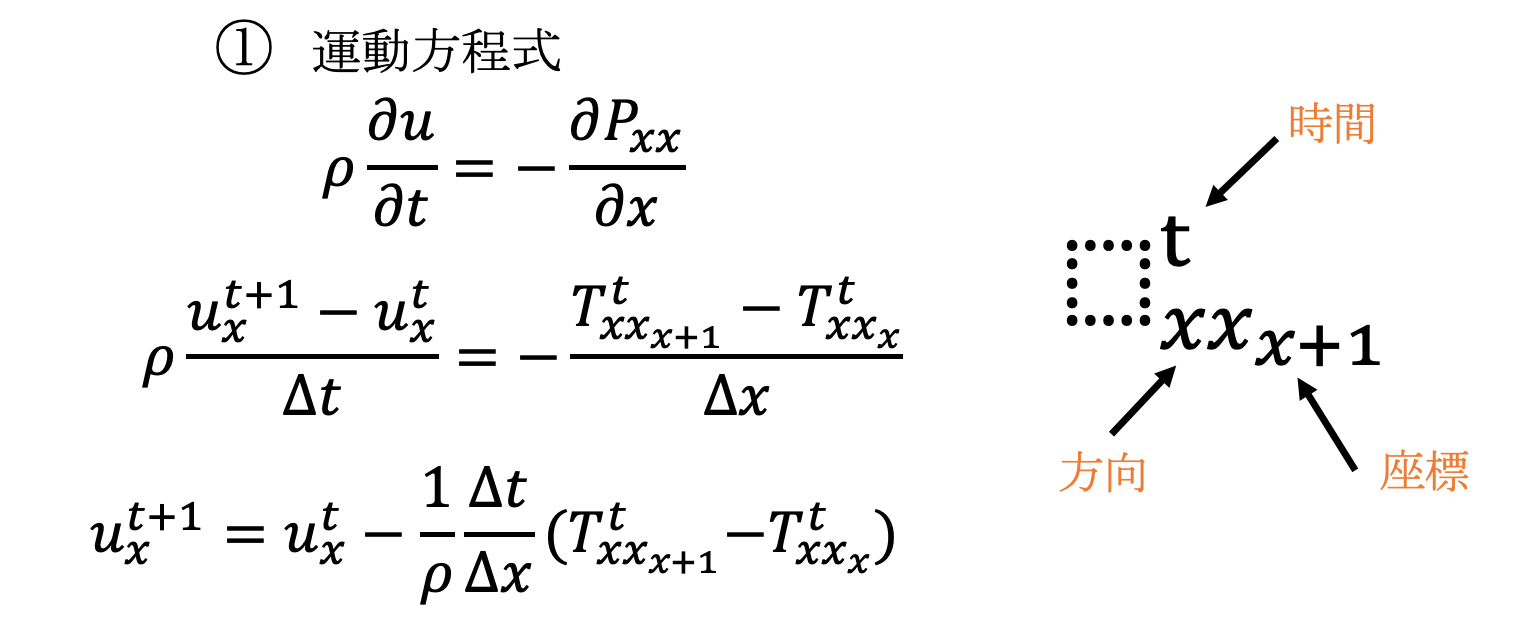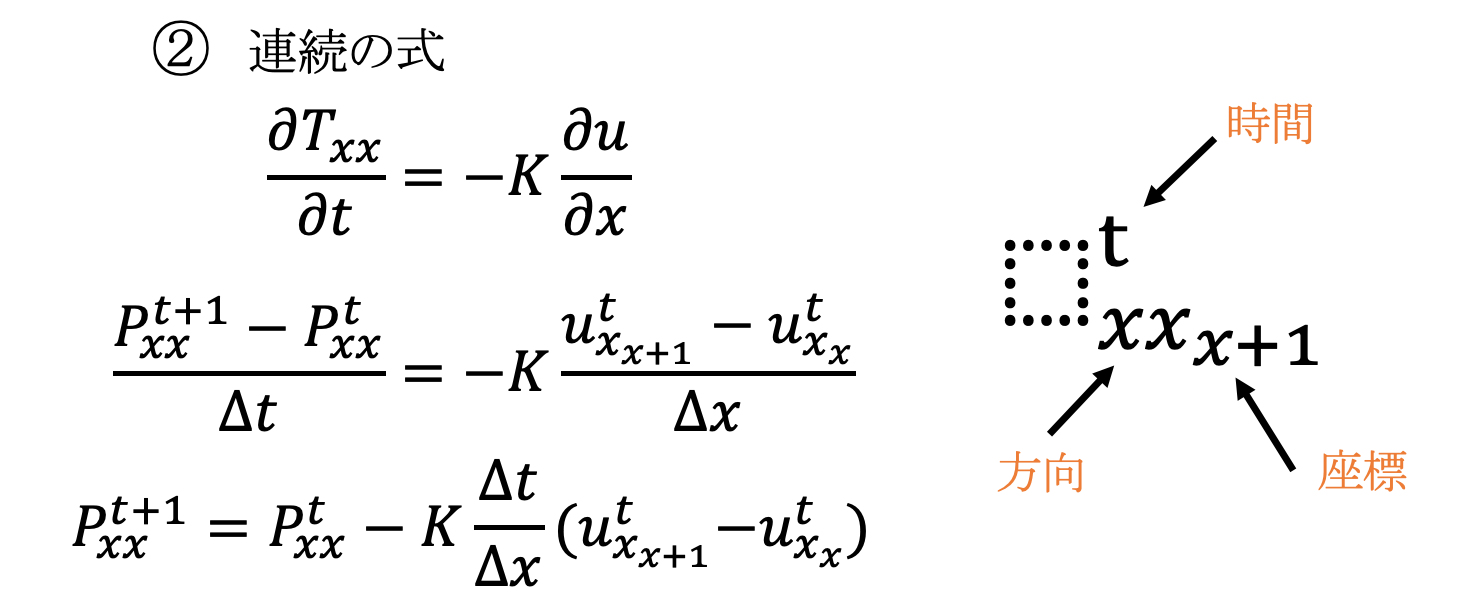はじめに
普段プログラミングを学んでいても、知る機会がないと思いこちらの記事を書きました。
シミュレーションのプログラムをまずは動かしてみて、楽しんでもらえたら幸いです。
そもそもシミュレーションって?
コンピュータ上で現象を観測や実験をすること
実物での実験ができなかったり、実験を行う前に検討する時に使います。
現実のモデル(環境)を作り、それを使って観測または実験することですね。
音響シミュレーションとは 読んで字のごとく、
音の現象をコンピュータ上で再現することです
今回紹介するのは音響FDTD法というものを紹介します。
これは、音の伝わり方などの観測に優れています。
そもそも音ってプログラムで書けるの?!
自分も最初は思ってました笑
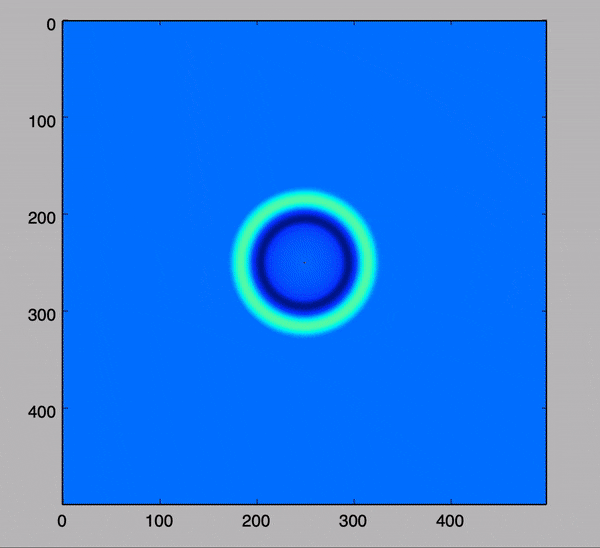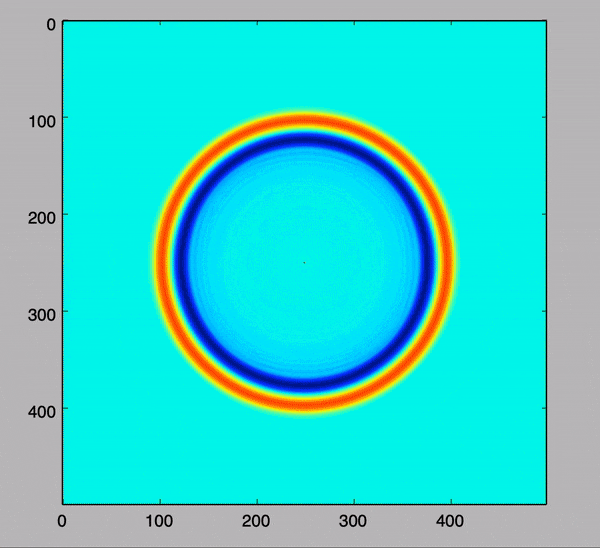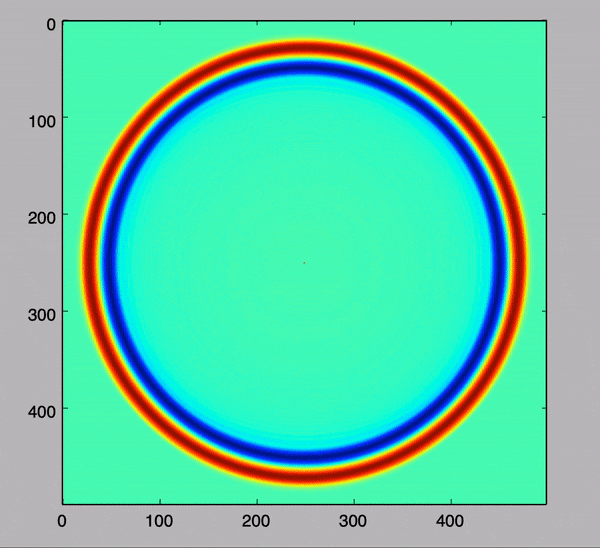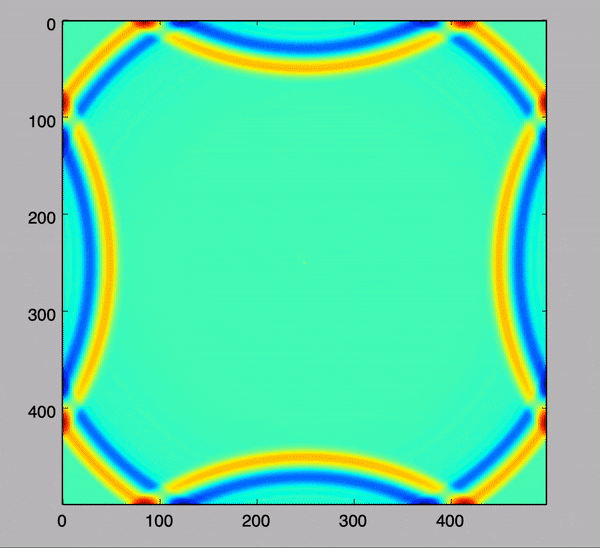
例は以下のものになります。
こちらは真ん中から1波を照射しているものです
音は以下の式で表現可能です。すごい!!

こんな式、プログラムで書けないでしょ!
偏微分とかをライブラリにあるのかな、、、。
難しそうって思った方ももう少し待ってください!
高校で習った最初の微分を思い出してみると、微分はある範囲の傾きということです。
右の図なら書けそうですよね?
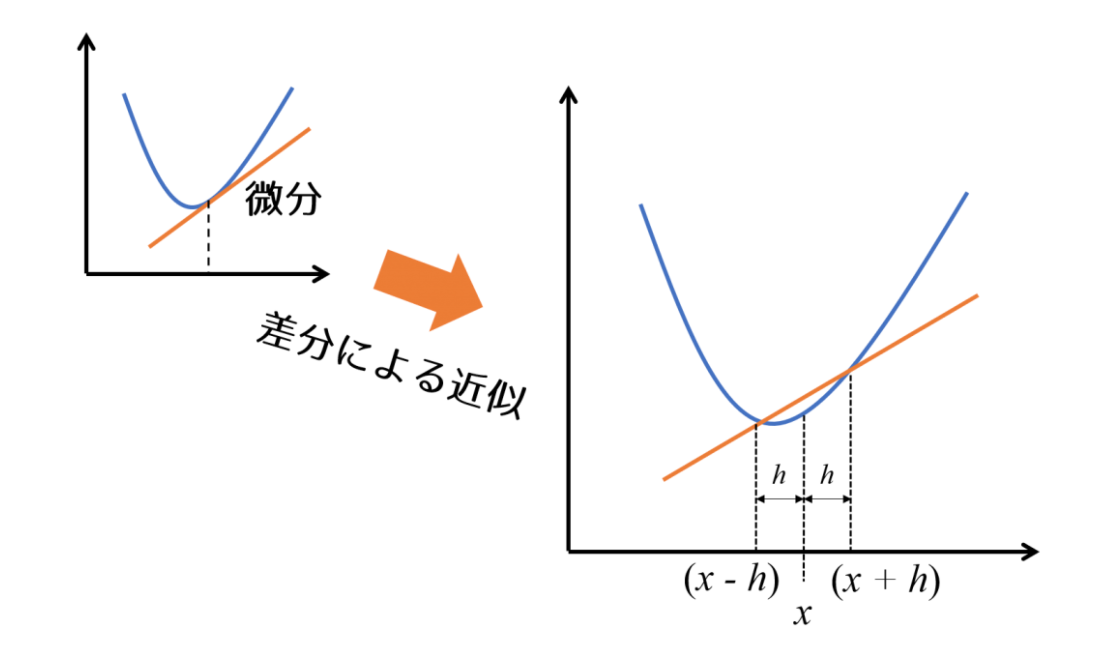
そして実際にPythonで書くとこちらです!!
1次元
Ux[1:nx] = Ux[1:nx] - 1/p * dt/dx * (Pxx[1:nx] - Pxx[0:nx-1])
Pxx[0:nx] = Pxx[0: nx] - K * dt/dx * (Ux[1: nx+1]-Ux[0: nx])
2次元
Ux[1: nx, 0: ny] = Ux[1: nx, 0: ny] - \
1/p * dt/dx * (Pxx[1: nx, 0: ny] - Pxx[0: nx-1, 0: ny])
Uy[0: nx, 1: ny] = Uy[0: nx, 1: ny] - \
1/p * dt/dy * (Pxx[0: nx, 1: ny] - Pxx[0: nx, 0: ny-1])
Pxx[0: nx, 0: ny] = Pxx[0: nx, 0: ny] - K * dt * \
((1/dx)*(Ux[1: nx+1, 0: ny]-Ux[0: nx, 0: ny]) + \
(1/dy)*(Uy[0: nx, 1: ny+1]-Uy[0: nx, 0: ny]))
時間軸はfor文で回すので考えなくて大丈夫です。
また、行列の中身の話をしようと思うと粒子速度と応力の関係についてもまた話さないといけないのでそれはまた後日。
今回使うライブラリをインストールしましょう。
pip install numpy
pip install math
pip install matplotlib
これをインストールできたらあとはコピペするだけです!笑
# -*-coding:utf-8-*-
# 2D_FDTD
import numpy
import math
import matplotlib.pyplot as plt
# 初期設定値(定数)
dimension = 2 #次元
rhow = 1000.0 #水密度
frequency = 1.0e+6 #周波数 1Mhz なんでも
vertical_wave_sound_velocity=1500.0 #水の縦波音速
T = 1/frequency
rhob = 2000.0
# 分解能 大きければ大きいほど精度が上がる
# 設定値によってはPCがフリーズするので注意
dx = 1e-5
dy = dx
dt = dx/vertical_wave_sound_velocity/math.sqrt(dimension)
# シミュレーション空間の範囲
model = numpy.zeros((500, 500))
nn = model.shape
nx = nn[0]-1
ny = nn[1]-1
nt = 1000
# 入力波形 今回は、sin 1波
n = int(T / dt)
wave2 = numpy.array([math.sin(math.pi * 2 / T * dt * ms)
for ms in range(0, n+2)])
# 音圧と音速行列を定義
Pxx = numpy.zeros((nx, ny), dtype=float)
Ux = numpy.zeros((nx+1, ny), dtype=float)
Uy = numpy.zeros((nx, ny+1), dtype=float)
# 音波発生位置 今回は、真ん中
inputpointx = int(nx/2)
inputpointy = int(ny/2)
for s in range(nt):
# 入力する波
if s <= n+2:
Pxx[inputpointx, inputpointy] = wave2[s-1]
else:
Pxx[inputpointx, inputpointy] = 0
# 波の伝わり方の計算
Ux[1: nx, 0: ny] = Ux[1: nx, 0: ny] - \
(1/rhow) * (dt/dx) * (Pxx[1: nx, 0: ny] - Pxx[0: nx-1, 0: ny])
Uy[0: nx, 1: ny] = Uy[0: nx, 1: ny] - \
(1/rhow) * (dt/dy) * (Pxx[0: nx, 1: ny] - Pxx[0: nx, 0: ny-1])
Pxx[0: nx, 0: ny] = Pxx[0: nx, 0: ny] - rhow * \
vertical_wave_sound_velocity ** 2 * dt * ((1/dx)*(Ux[1: nx+1, 0: ny]-\
Ux[0: nx, 0: ny]) + (1/dy)*(Uy[0: nx, 1: ny+1]-Uy[0: nx, 0: ny]))
# シミュレーションの表示
if s % 5 == 0:
print("count: {0}".format(s))
plt.cla()
plt.imshow(Pxx, vmin=-
1, vmax=1, origin=0)
plt.draw()
plt.pause(0.00001)
センサの場所を色々設定するとおもしもいです。(これは、四隅と真ん中)
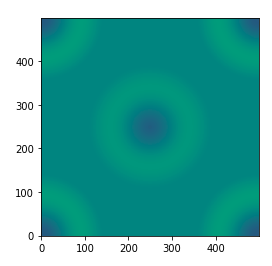
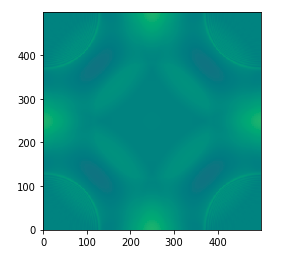
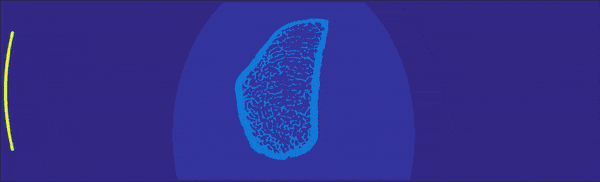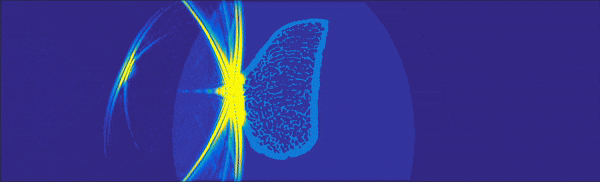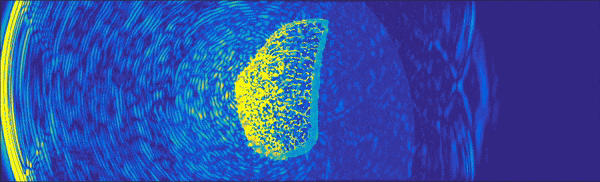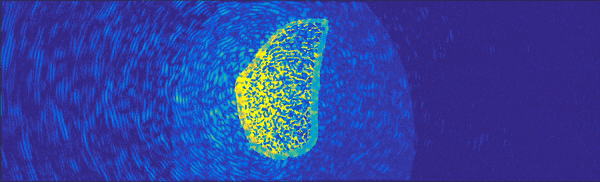
modelに画像とかを入れてみたりするとこんな感じになります。
よりシミュレーションっぽいですね。
まとめ
GoogleColabをみてもらうかぜひコピペしみて試してみてください🙏
音響の現象も様々で、音の伝播(伝わり方)、反射、回折、吸収などなどの様々な現象があります。
また、興味を持ったらFDTDシミュレーションって調べてみると詳しい記事もあるのでみてみてください。
こちらでDMMのアドベントカレンダーは最後になります。
おもしろい記事がいっぱいあるのでぜひ他のものもみてください!
ではまた来年👋