CS(コンピューターサイエンス)基礎の基礎
現在、CS基礎の基礎を一から学んでいるので、その学習成果のアウトプットに、、、
今回はCSを基礎から学習できるサービス「 Recursion」を参考にさせていただきました。興味のある方は以下からどうぞ!
↓↓↓↓↓↓
Recursion
今回は「データとデータ型」
1.データとは
データとは、 コンピューターで処理される特定の順序で示された記号や数字 のことを指します。
このデータを人間が理解できる形として示されているものを 情報 と呼びます。
2.データ型とは
前提として コンピュータはデータを「0」と「1」の2種類の数字の組み合わせでのみ表現する ことができます。
その時、組み合わせて表現されたものが どのような種類のデータを示すのか を判断できないと意味がないですね。その時に使用されるのが、 「データ型」 です。
例えば、プログラムで 「1」 と打った時と 「"1"」 と打った時では、人間は同じ1だと判断しますが、コンピューターは違う種類のデータだと判断します。これは、「1」は 「整数型」 というデータ型であり、「"1”」は 「文字列型(言語によっては『文字型』)」 というデータ型のため、違う種類だと判断されるからです。このようにして、「0」と「1」でしか表現できないデータを様々な種類で使用していくことができます。
#Rubyの場合
puts 1 #「整数型」の「1」だと認識される
puts "1" #「文字列型」の「1」だと判断される
puts 1 + 1 #結果は「2」
puts "1" + "1" #文字列の連結と判断され、結果は「11」
上記はあくまでRubyの場合のデータ型です。言語ごとに用意されているデータ型が異なるので、逐一確認するようにしましょう。
3.データ型の種類
3-1. Boolean(ブーリアン)型
コンピュータは「0」と「1」のみで表現しますが、その基本的な考え方を用いて、2通りのみで表現できるデータとして、 「真偽値」 があります。「1」を「True」、「0」を「False」のようにして扱い、その 「真偽値を出力するため」 に使用する型が Boolean型 です。
【具体例】
●アンケート機能の「はい」、「いいえ」
●チェックボックスにチェックを「入れた」、「入れていない」
●金融機関の預金口座に「預金した」、「預金していない」
#Ruby
puts true #結果は「true」
puts false #結果は「false」
3-2. Integer(整数)型
0と1の組み合わせの方法を増やすことで、日常的に用いるような整数を表現することができるようになります。そのための型 を Integer型 と言います。
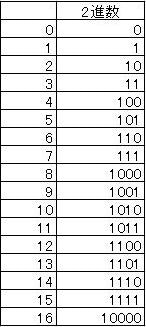
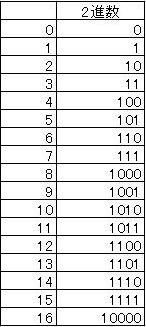
普段私たちは 10進法 を用いて、「0 1 2 3 4 5 6 7 8 9」の10個の数字の組み合わせで整数を表現していますが、コンピューターは先ほどの「0」と「1」の組み合わせ、つまり 2進数 で表現しています。この 10進数と2進数を対応させることで整数を表現 することができるのです。
※「bit」と「byte」
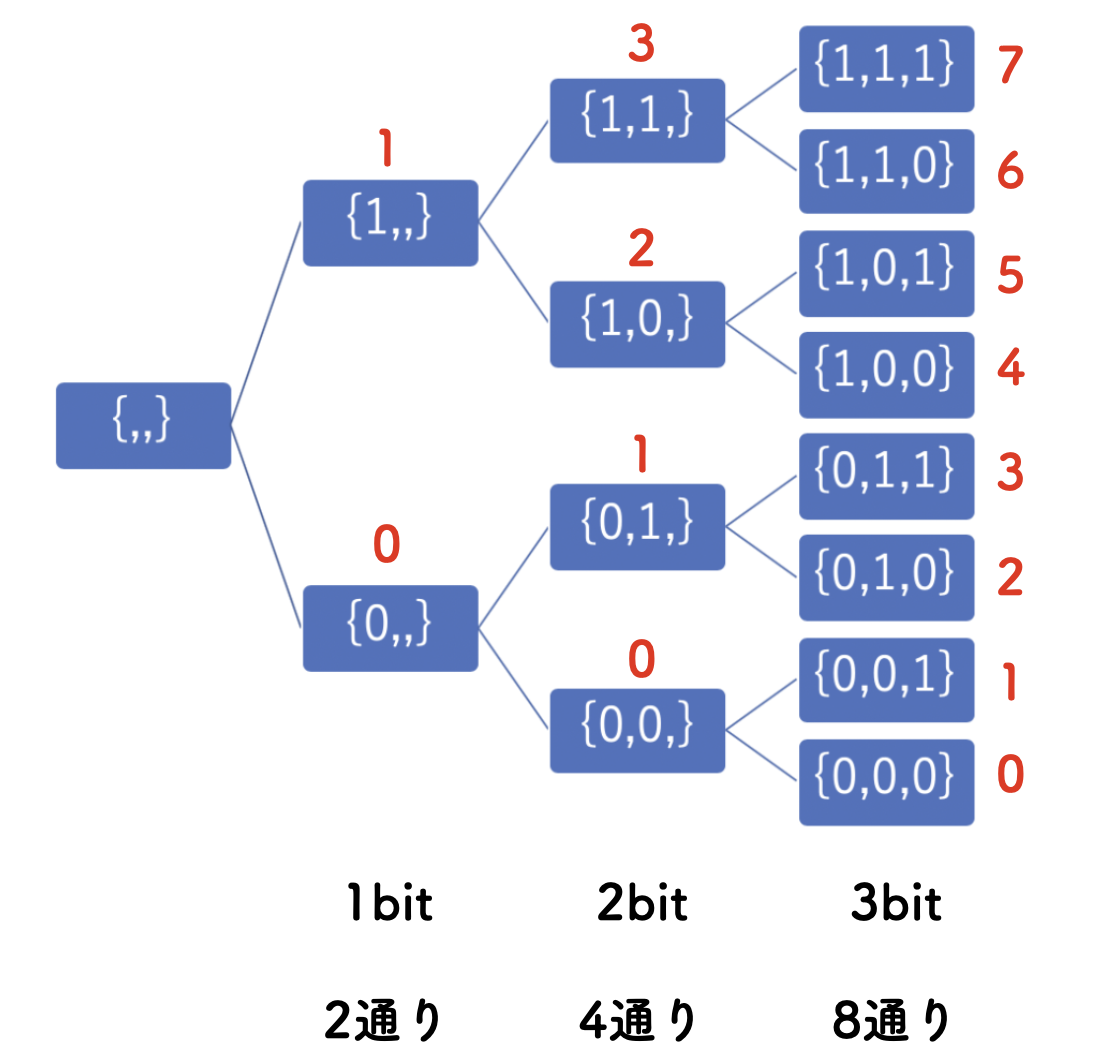
先ほどコンピューターは「0」と「1」の2種類の組み合わせで表現すると示しましたが、この組み合わせの要素一つ一つのことを bit と呼びます。 この「bit数が大きくなる = コンピューターで保存できるデータの領域が増える」 ことにより、表現できる値の種類が増えていきます。
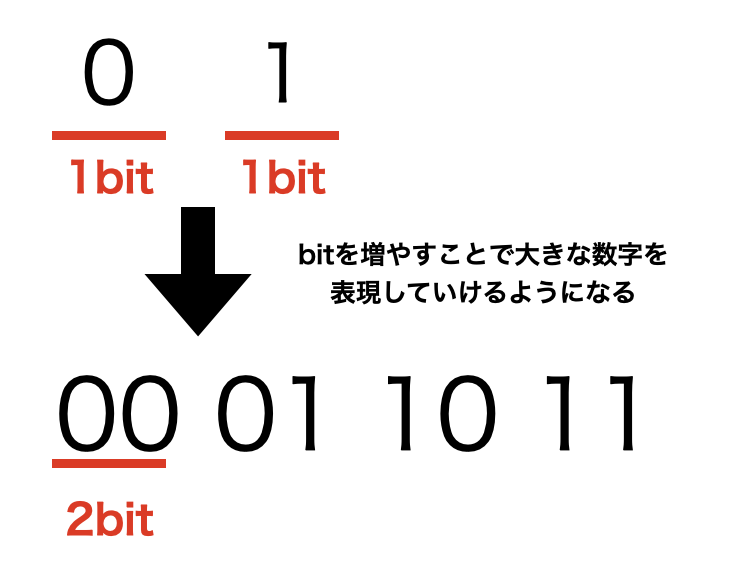
このように、「1」と「0」をそれぞれ「1bit」と基準点とし、そこから 「n bitはn個の数字の組み合わせの要素が2n乗通り」 のように表現できる数が増えていきます。
このbitが 8bit に達すると、 1byte となります。1byteは8bitなので、2の8乗つまり 256通り の整数表現ができるようになります。
この考えを利用し、整数型では「桁数」という概念で表現できる値の種類を判断するのではなく、「byte数」で判断するようになります。整数型はデフォルトで「4byte」であるため、2の32乗通りの表現が可能です。 プログラミング言語によっては、表現できる数の上限が設けられている ようです。
※16進数
上のように、10進数は人間が扱いやすく可読性にも優れています。一方 2進数はコンピューターにとって扱いやすいですが、数字が大きくなれば2進数で表現する時の桁数も増え、人間にとってはかなり可読性という点で劣っています 。
この点を踏まえて使われるのが 16進数 です。
16進数は「0 1 2 3 4 5 6 7 8 9 A B C D E F」の16個の組み合わせで表現する ものです。
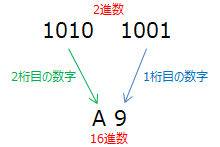
このように、16進数で表現したものを2進数に変換すると、4bitの数の組み合わせで表現できるようになり、可読性が増すようになります。長ければ長いほど、16進数と2進数の対応表記法は便利になります。
16進数は 「IPアドレス」 や 「文字コード」 などの冗長になりやすい値に広く使われているそうです。
3-3. Char(文字)型
0と1の2進数の組み合わせを文字と対応させて表現する のが Char型 です。
そもそもコンピュータは文字というものを識別できません。だからこそ、 文字とそれに対応するコードを用意しておき、コンピュータがそのコードを読み取ることで文字に変換できるようにする という技術を使って文字を出力しています。
この「文字とコードの対応」は誰でも決めることができますが、誰でも決めることができてしまうと、コンピュータによって文字とコードの対応が違ってしまい、使いづらくなってしまいます。
そこで登場したのが「文字コード」と呼ばれるものになります。これは文字とコードの対応を表にして、世界基準で使用していこうという意図で作成されたものです。最も古い文字コードには「ASCII」というものがあり、これは英語のみに対応した文字コードでした。
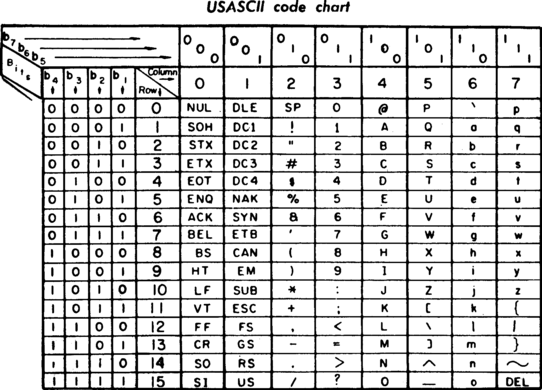
これは、ASCIIの文字コード表ですが、各文字を2進数ではどのように表現するのかが定義されているのが分かります。例えば、「A」という文字だと、「1000001」の7bitで表現されるという具合です。
しかし、ASCIIでは英語しか対応していないため、他の言語にも対応させたいところですよね。そこで生まれたのが、「Unicode」と呼ばれるものになります。これは、世界中の言語に対応しているものになりますが、厳密には「文字コード」ではありません。一つ一つの文字に「コードポイント」と呼ばれる数字を割り振っているだけのものになります。つまり、このUnicodeそのものをコンピュータが理解することは出来ません。
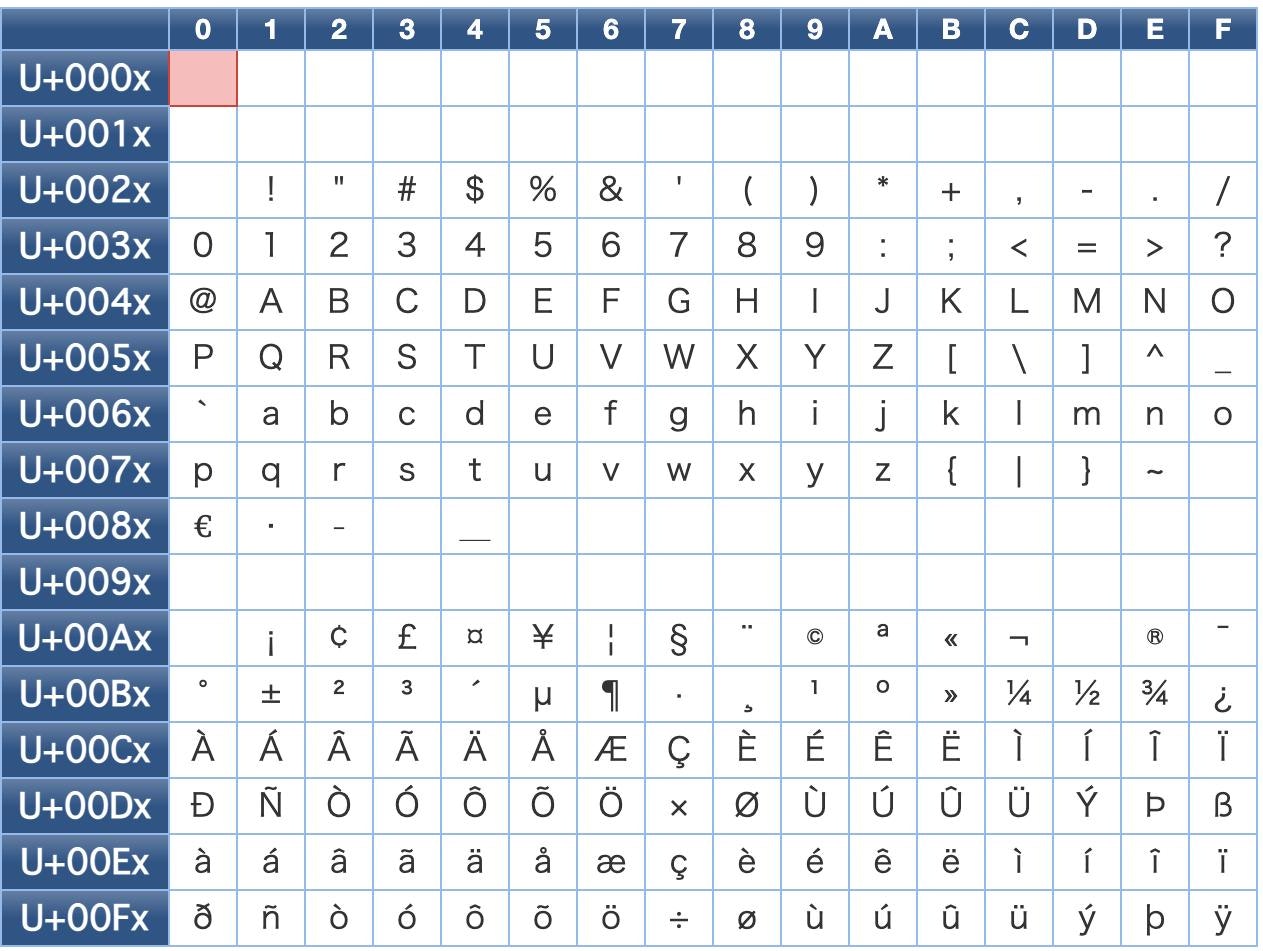
この unicodeのコードポイントをコンピュータが実際に理解できるコードに変換するための対応表として作られた のが、かの有名な「UTF-8」です。unicodeからUTF-8へと変換する仕組みは以下の図のとおりです。
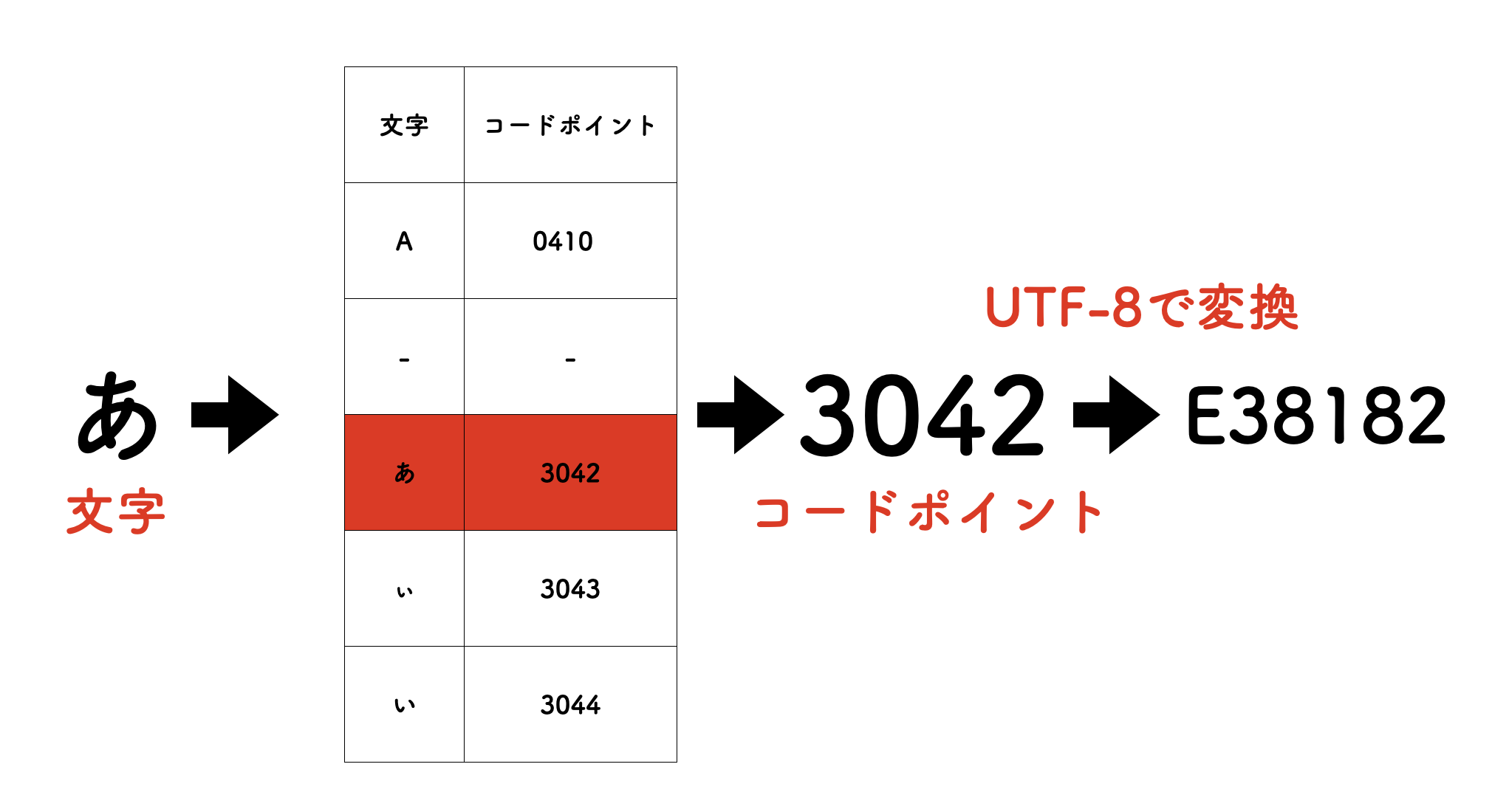
unicodeのコードポイントに応じた変換ルールが決まっているため、それに応じてUTF-8用の変換をします。上の図では変換後のコードを16進数で表記していますが、実際にはコンピュータは2進数で識別します。
また、 UTF-16 という文字コードもあり、これはUTF-8とはまた違った対応ルールを持っています。

UnicodeやUTF-8はそれぞれ上の図のように呼ばれています。難しいので理解しなくてもいいと思います。
しかし 「文字コード」は「文字化け」などの原因にもなる存在でもあるため、その対応のために知っておくことは必要だと言えます。
3-4. String(文字列)型
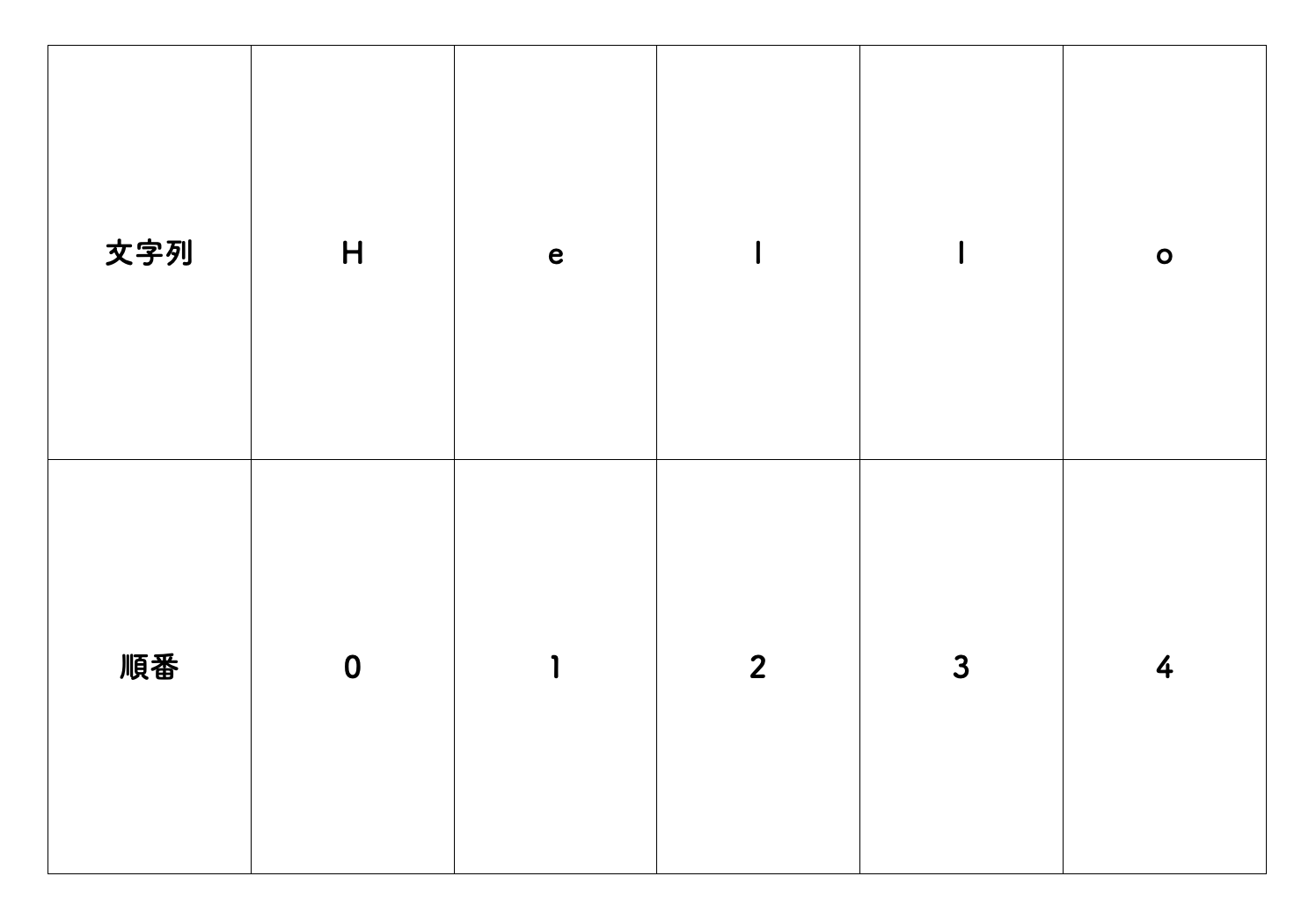
上の 「Char型」の文字一つ一つを配列のように順番に並べて文章のように表現する のが String型 です。
言語によっては、「Char型」と「String型」が両方存在しているものもあれば、「String型」のみに纏められているものもあります。
3-5. 浮動小数点型
3-5-1. 固定小数点数について
まず、コンピュータの世界には「 固定小数点数 」と「 浮動小数点数 」というものがあります。固定小数点数とは、「 小数点が決まった位置にあるという前提で扱う少数 」を指します。コンピュータは、小数点の「.」は理解できません。そのため、整数を覚えさせて、「 その整数の決まった位置に点を打つ」というように覚えさせるわけです。こうすることで 決まった位置に小数点の打たれた固定小数点数 を表現できるのです。
3-5-2. 浮動小数点数について
固定小数点数は決まった位置に小数点を置いて扱うやり方です。しかし、この方法では、 コンピュータのメモリは有限のため、とても大きい値や逆にとても小さい値を扱うことができません 。
そのため、通常コンピュータでは「 浮動小数点数 」として少数を扱います。これは、「3.1×10^8, 0.31×10^9」のように「 何乗形式 」で扱う少数を指します。コンピュータには、「3.1×10^8」の例で言えば、「3.1」と「8」の部分のみを記憶させるようにします。こうすることで、 少ないメモリでもより小さな値やより大きな値を表現できるようになります。
実際に表記するときは、「固定小数点数」と「浮動小数点数」という区別はあるものの、コンピュータで表現するときは、例えばRubyであれば、固定少数点数の表記をした値も、浮動小数点数のE表記をした値も、「データ型」としては浮動小数点型の「 Float型 」が適用されることになります。
3.14159285 #Float型
3.1E+8 #Float型
31.4E+7 #Float型
まとめると、
固定小数点数は、「 小数点が決まった位置にあるという前提でコンピュータに記憶させて扱うもの 」であり、浮動小数点数は、「 指数を使った表記をすることで扱える数値の範囲を増やしたもの 」と言えます。
浮動小数点数は「 計算などで誤差が生じる(コンピュータが10進数で入力された少数を2進数に変換するときに生じる) 」という点もありますが、コンピュータの世界では広く一般的に使われているということですね。
4.学び
プログラミングでデータベース設計で何気なく指定している「カラム型」も、よくよく考えてみると、これだけの基礎知識に基づいたものなのだと改めて実感しました。
今後「型」を決めるときに、今回学んだ視点も取り入れながら実装してみようと思います。