ブラシDCモーターにPWM制御をかけたときの電流とか回転数が見たくなりました。
ステップ入力を印加した時と、PWMのデューティ比を徐々に上げたときで、それぞれシミュレーションします。
モデリング
以下ではモーターの微分方程式を解いていきます。つまり積分の式を求める。
しかし、シミュレーションでは微分方程式をそのまま使うので、積分の式が欲しい人以外は読み飛ばしてよいです。
回路方程式
まずは、モーターのモデリングです。
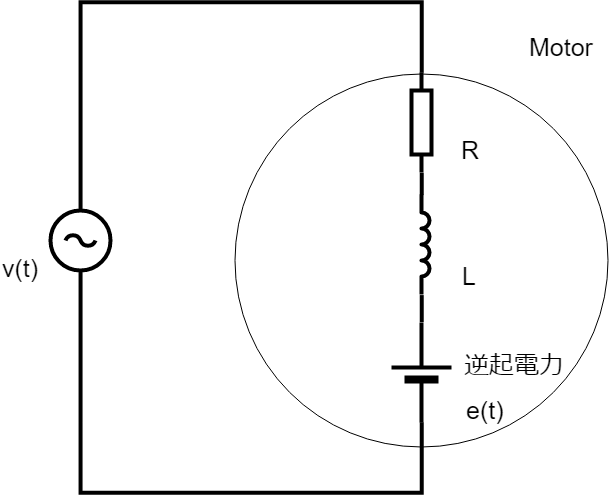
電圧v(t)を印加したブラシDCモータの等価回路は以下の図のようにします。
抵抗R、インダクタンスL、逆起電力e(t)としてモータ内の要素を表します。
この回路の微分方程式は以下で表されます。
v(t)=L \frac{d i(t)}{d t}+R i(t)+e(t)
この微分方程式の解を求めます。
定数変化法によって解いていくと
まずは斉次、
L \frac{d i(t)}{d t}+R i(t)=0
の解は、
i(t)=C e^{-\frac{R}{L} t} (Cは積分定数)
であるので、ここで積分定数CをC1(t)として、
i(t)=C_{1}(t) e^{-\frac{R}{L} t}
です。またこの微分
\frac{d i(t)}{d t}=\frac{d C_{1}(t)}{d t} e^{-\frac{R}{L} t}-\frac{R}{L} C_{1}(t) e^{-\frac{R}{L} t}
をそれぞれ最初の式に代入して、
v(t)-e(t)=L \frac{d C_{1}(t)}{d t} e^{-\frac{R}{L} t}
が得られます。
C1(t)について解くと、
C_{1}(t)=\int_{0}^{t} \frac{1}{L}\{v(\tau)-e(\tau)\} e^{\frac{R}{L} \tau} d \tau+C_{1} (C_{1}は積分定数)
と求まります。したがって、代入すれば、
i(t)=e^{-\frac{R}{L} t}\left\{\int_{0}^{t} \frac{1}{L}\{v(\tau)-e(\tau)\} e^{\frac{R}{L} \tau} d \tau+C_{1}\right\}
とi(t)の式が求まりました。
しかし、まだ終わりではありません。
逆起電力e(t)の式を求める必要があります。
逆起電力e(t)はモータの角速度に比例し、以下の式で表されます。Kは逆起電力定数です。
e(t)=K \omega(t)
機械系の運動方程式
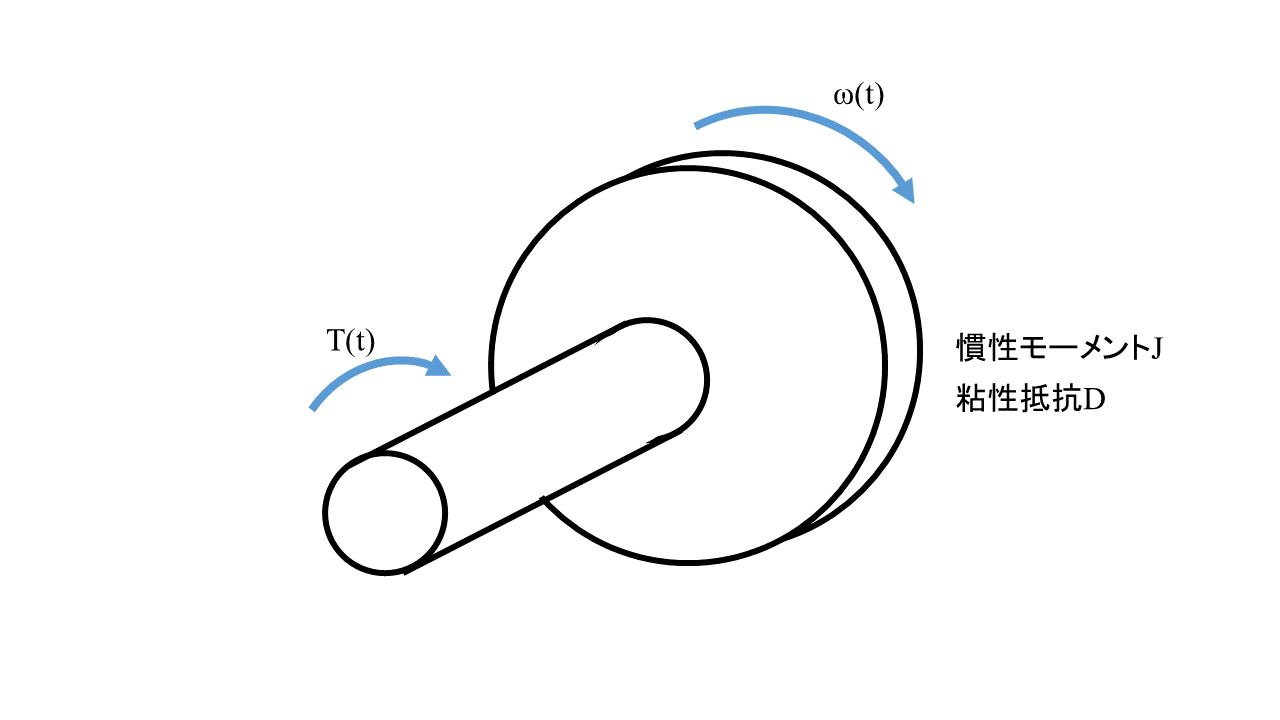
ω(t)を求めるためにブラシDCモーターの機械的なモデリングを行います。
ブラシDCモータをトルクT(t)を入力した軸として図のようにします。
この機械系の微分方程式は以下の式で表されます。
T(t)=J \frac{d \omega(t)}{d t}+D \omega(t)
やはり定数変化法で解くと、同様に
C_{2}(t)=\int_{0}^{t} \frac{1}{J} T(\tau) e^{\frac{D}{J} \tau} d \tau+C_{2}
\omega(t)=e^{-\frac{D}{J} t}\left\{\int_{0}^{t} \frac{1}{J} T(\tau) e^{\frac{D}{J} \tau} d \tau+C_{2}\right\} (C_{2}は積分定数)
とω(t)の式が得られました。
また、T(t)は電流i(t)に比例し、以下の式で表されます。
T(t)=K i(t)
式のまとめ
微分系
今回つかうのはこちら。
v(t)=L \frac{d i(t)}{d t}+R i(t)+e(t)
e(t)=K \omega(t)
T(t)=J \frac{d \omega(t)}{d t}+D \omega(t)
T(t)=K i(t)
積分系
i(t)=e^{-\frac{R}{L} t}\left[\int_{0}^{t} \frac{1}{L}\{v(\tau)-e(\tau)\} e^{\frac{R}{L} \tau} d \tau+C_{1}\right]
e(t)=K \omega(t)
\omega(t)=e^{-\frac{D}{J} t}\left[\int_{0}^{t} \frac{1}{J} T(\tau) e^{\frac{D}{J} \tau} d \tau+C_{2}\right]
T(t)=K i(t)
シミュレーション
ステップ応答と、PWM入力の応答でそれぞれシミュレーションします。
pythonでコードを書いて実行します。
scipyでシミュレーションして図はmatplotlibで出力。
コード
デューティ比は0.5です。
from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
# maxon RE40 グラファイトブラシ, 150 Watt 製品番号 148867
R = 0.299 #[Ω]
L = 0.082e-3 #[H]
J = 142.0e-7 #[kgm^2]
tau_m = 4.67e-3 #[sec]
D = J/tau_m #[Nm sec/rad]
E = 24.0 #[V]
K = 30.2e-3 #[Nm/A]
f = 20e+3
def motorStep(var, t):
i = var[0]
omega = var[1]
e = K*omega
T = K*i
if t < 0.000002:
v = 0
else:
v = E
didt = 1/L * (v - R*i - e)
domegadt = 1/J * (T - D*omega)
return [didt, domegadt]
def motorFromPWM(var, t):
i = var[0]
omega = var[1]
e = K*omega
T = K*i
if t < 0.000002:
pwm = 0.0
else:
pwm = ( (np.sin(2*np.pi*f*t)+0.9999) ).astype(np.int)*E
pwm = pwm.astype(np.float)
didt = 1/L * (pwm - R*i - e)
domegadt = 1/J * (T - D*omega)
return [didt, domegadt]
var_0 = [0.0, 0.0]
t = np.arange(0, 0.1, 0.000001)
var_list_step = odeint(motorStep, var_0, t)
var_list_pwm = odeint(motorFromPWM, var_0, t)
fig, ax = plt.subplots(1,2)
ax[0].plot(t, var_list_step[:, 0], label='step', ls='-')
ax[0].plot(t, var_list_pwm[:, 0], label='pwm', ls='-.')
ax[0].set_xlabel('t')
ax[0].set_ylabel('i[A]')
ax[0].legend(loc='best')
ax[0].grid(ls=':')
ax[0].set_title('Current')
ax[1].plot(t, var_list_step[:, 1]*60/(2*np.pi), label='step', ls='-')
ax[1].plot(t, var_list_pwm[:, 1]*60/(2*np.pi), label='pwm', ls='-.')
ax[1].set_xlabel('t')
ax[1].set_ylabel('$\omega[rpm]$')
ax[1].legend(loc='best')
ax[1].grid(ls=':')
ax[1].set_title('Speed')
plt.subplots_adjust(wspace=0.4)
plt.savefig('MotorSimResult.png')
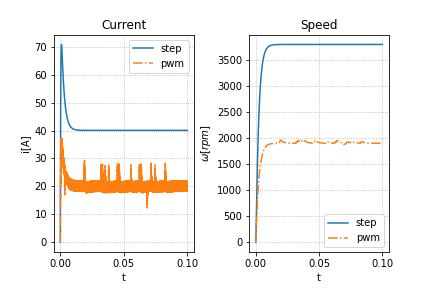
シミュレーション結果
左は電流、右は回転数です。
デューティ比を0.5に設定してあるのでPWM制御した場合の方だと電流が約1/2倍になっていますね。
始動電流もある程度抑えられています。
実験
完全に別ものですが、モータに流れる電流を電流センサで読み取ってみました。
モーターはRS-540
センサはACS714
印加電圧は8 V程度
制御はmbed LPC1768です。
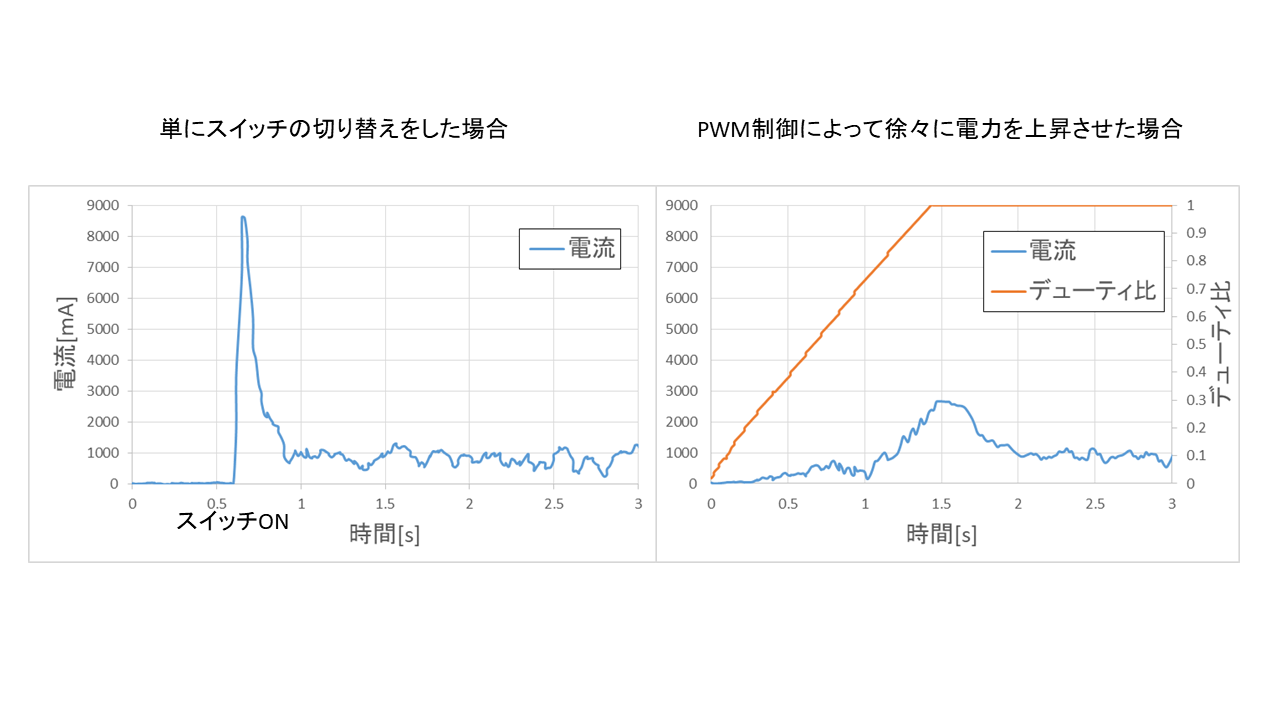
実験結果
単純に電圧を印可した場合(左)、デューティ比を線形に上げた場合(右)です。
確かにデューティ比が1になったときに始動電流らしきものが発生しています。