はじめに
MATLAB Student Ambassadorとして活動を開始してから1年が経とうとしています. ここまで支えていただいたたくさんの方々に感謝申し上げます. そして, この節目に, これまで私の活動を支えてくれたMATLABコードたちをまとめておこうと考え, 記事にしました.
この記事では, MATLAB R2021bを使用しております.
また, 本記事で示されたコードは, 今回対象とした問題以外での検証等は行っておりません.
ラグランジュ補間
ラグランジュ補間は, 以下の式で定義されています.
f(x) = p_n(x) = \sum_{k=1}^nL_k(x)f_k \\
L_k(x) = \frac{l_k(x)}{l_k(x_k)} \\
l_k(x) = (x-x_1)(x-x_2)\cdots(x-x_{k-1})(x-x_{k+1})\cdots(x-x_n)
ここで, $x_k$は標本点のある位置, そして, $f_k$は$x_k$における標本データを表しています. 今, $x_1\cdots x_k\cdots x_n$という位置において, $f_1\cdots f_k\cdots f_n$という標本データが与えられており, $x'_1\cdots x'_m$における近似値$f'$を計算したいとすると, 上の式で表されている定義は, 下の行列による表現に書き換えることが可能です.
f' = \left[\begin{array}{ccccc}
f_1 & \cdots & f_k & \cdots & f_n
\end{array}\right]
\left[\begin{array}{ccc}
L_1(x'_1) & \cdots & L_1(x'_m) \\
\vdots & \vdots & \vdots \\
L_k(x'_1) & \cdots & L_k(x'_m) \\
\vdots & \vdots & \vdots \\
L_n(x'_1) & \cdots & L_n(x'_m)
\end{array}\right]
これらの式を用いて, MATLABで関数を作成する.
MATLABの補間関数 interp1
MATLABには既にとても使いやすい補間の関数として, interp1が存在します. そこで, 作るラグランジュ補間の関数はできるだけ, interp1に似せた入出力を持たせることにしました (これでMATLABで補間をする方法を学んでくれる人がいると嬉しい).
interp1の基本的な使い方としては,
vq = interp1(x,v,xq)
のように,
- $x$ : 標本データのある位置
- $v$ : 標本データ
- $xq$ : 近似値の計算が必要な位置
が入力であり,
- $vq$ : 補間で得られる値
が出力となっています.
作成したMATLAB関数 interpLagVector1
ここでは, $x$, $v$, $xq$がすべてベクトルであると仮定します. この仮定を踏まえて作成したMATLAB関数interpLagVector1が以下になります.
function vq = interpLagVector1(x,v,xq)
%
% interpLagVector1 - Lagrange Interpolation
%
% vq = interpLag1(x,v,xq)
%
% -Inputs-
% x - Sample Points
% v - Sample Values
% xq - Query Points
%
% -Outputs-
% vq - Interpolation Value
%
% --- Usage Example ---
%
% x = 0:pi/4:2*pi;
% v = sin(x);
% xq = 0:pi/16:2*pi;
% vq = interpLagVector1(x,v,xq);
% plot(x,v,'o',xq,vq1,':.');
%
% ---------------------
%
%
if (isvector(x) && isvector(v) && isvector(xq))
% Setting
n = length(x); % Get Number of Cotrol Points
nq = length(xq); % Get Number of outputting Points
L = ones(n,nq); % Create Matrix for Lagrange Equation
% Unify All variables to Row Vector
x = reshape(x,[1,n]);
v = reshape(v,[1,n]);
xq = reshape(xq,[1 nq]);
% Create Lagrange Equation
for ii = 1:n
for jj = 1:nq
for kk = 1:n
if (ii ~= kk)
L(ii,jj) = L(ii,jj)*(xq(jj)-x(kk))/(x(ii)-x(kk));
end
end
end
end
vq = v*L; % Get Answer
else
error('Error!! All inputs should be Vector.');
end
end
ここで, MATLABでは, 関数の作成と同時に, その中身の説明を加えることができます.
interpLagVector1の確認
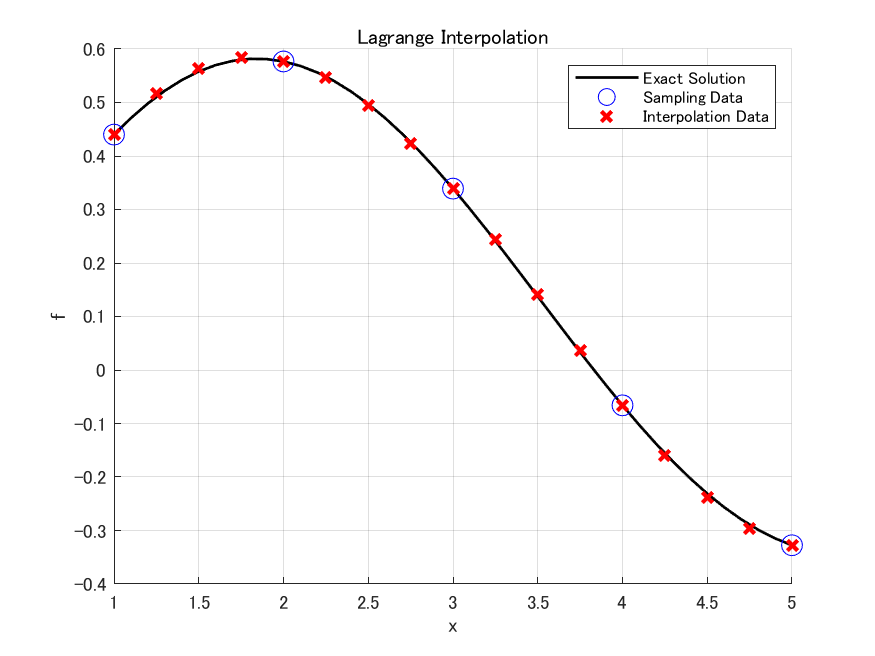
ここでは, ベッセル関数(besselj)を用いて作成したinterpLagVector1を試してみました.
%% Setting
start = 1;
stop = 5;
%% Single Data Interpolation
% Create Sampling Data
x = start:stop;
v = besselj(1,x);
% Exact Solution
x_ex = start:0.1:stop;
v_ex = besselj(1,x_ex);
% Interpolation
xq = start:0.25:stop;
vq = interpLagVector1(x,v,xq);
% Visualize
figure
hold on
plot(x_ex,v_ex,'k-','LineWidth',1.3);
plot(x,v,'bo','MarkerSize',10);
plot(xq,vq,'rx','LineWidth',2.0,'MarkerSize',7);
hold off
grid on
title('Lagrange Interpolation');
xlabel('x');
ylabel('f');
legend("Exact Solution","Sampling Data","Interpolation Data");
MATLAB補間関数への行列の入力
MATLABにある補間の関数interp1では, $v$及び$xq$について行列を入力することも可能です. この場合, 複数のデータの補間を計算したり, あるデータから異なる点での補間の値を算出することができます. そこで, 今回は, MATrix LABoratoryで行列を入力としたラグランジュ補間を行ってみました.
作成した関数 interpLag1
ここでは, $x$はベクトルであり, $v$, $xq$のうち少なくとも片方はベクトルであると仮定します. この仮定を踏まえて作成したMATLAB関数interpLag1が以下になります. この関数では先に作成したinterpLagVector1を用いています.
function vq = interpLag1(x,v,xq)
%
% interpLag1 - Lagrange Interpolation
%
% vq = interpLag1(x,v,xq)
%
% -Inputs-
% x - Sample Points
% v - Sample Values
% xq - Query Points
%
% -Outputs-
% vq - Interpolation Value
%
% --- Usage Example ---
%
% x = 0:pi/4:2*pi;
% v = sin(x);
% xq = 0:pi/16:2*pi;
% vq = interpLag1(x,v,xq);
% plot(x,v,'o',xq,vq1,':.');
%
% ---------------------
%
%
if (isvector(x))
if (length(x) == length(unique(x)))
if (isvector(v) && isvector(xq))
vq = interpLagVector1(x,real(v),xq) + 1i*interpLagVector1(x,imag(v),xq);
elseif (isvector(v))
vq = zeros(size(xq));
for ll=1:length(xq(1,:))
vq(:,ll) = interpLagVector1(x,real(v),xq(:,ll)) + 1i*interpLagVector1(x,imag(v),xq(:,ll));
end
elseif (isvector(xq))
vq = zeros(length(xq),length(v(1,:)));
for ll=1:length(v(1,:))
vq(:,ll) = interpLagVector1(x,real(v(:,ll)),xq) + 1i*interpLagVector1(x,imag(v(:,ll)),xq);
end
else
error('Error!! Either v or xq should be vector.');
end
else
error('Error!! x should not has same data.');
end
else
error('Error!! The input should be Vector.');
end
end
% Lagrange Interpolation
function vq = interpLagVector1(x,v,xq)
if (isvector(x) && isvector(v) && isvector(xq))
% Setting
n = length(x); % Get Number of Cotrol Points
nq = length(xq); % Get Number of outputting Points
L = ones(n,nq); % Create Matrix for Lagrange Equation
% Unify All variables to Row Vector
x = reshape(x,[1,n]);
v = reshape(v,[1,n]);
xq = reshape(xq,[1 nq]);
% Create Lagrange Equation
for ii = 1:n
for jj = 1:nq
for kk = 1:n
if (ii ~= kk)
L(ii,jj) = L(ii,jj)*(xq(jj)-x(kk))/(x(ii)-x(kk));
end
end
end
end
vq = v*L; % Get Answer
else
error('Error!! All inputs should be Vector.');
end
end
interpLag1の確認
ここでも, ベッセル関数(besselj)を用いて, 作成したinterpLag1を試してみました.
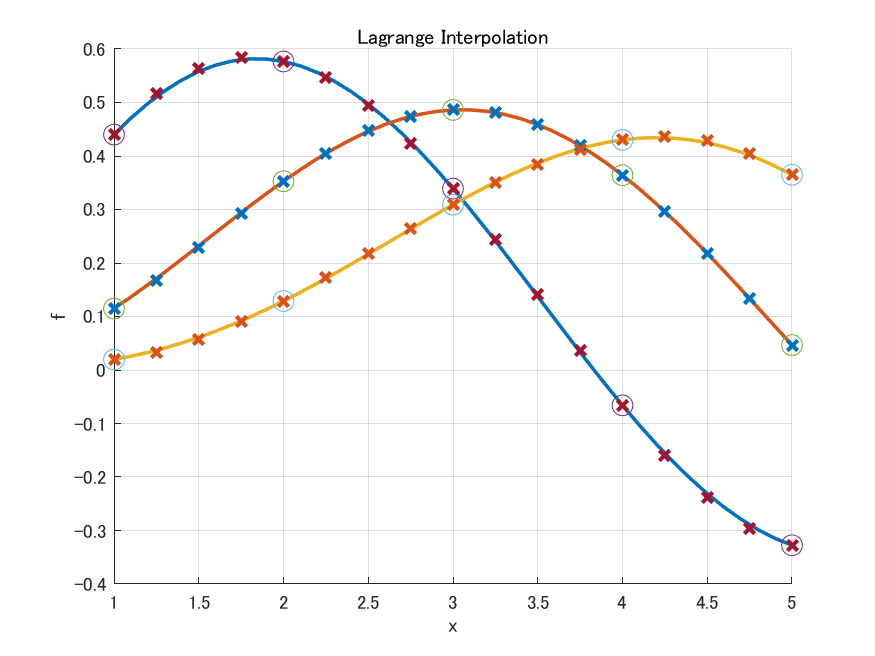
複数のデータのラグランジュ補間
ここでは, 1次, 2次及び3次のベッセル関数から標本データ$v$を取得し, ベクトル$xq$の各点における補間の値$vq$を算出しました.
clear all; close all; clc;
%% Setting
start = 1;
stop = 5;
%% Multiple Sample Interpolation
% Number of Data
n = 3;
% Create Sampling Data
x = start:stop;
v = zeros(length(x),n);
for ii = 1:n
v(:,ii) = besselj(ii,x);
end
% Exact Solution
x_ex = start:0.1:stop;
v_ex = zeros(length(x_ex),n);
for ii=1:n
v_ex(:,ii) = besselj(ii,x_ex);
end
% Interpolation
xq = start:0.25:stop;
vq = interpLag1(x,v,xq);
% Visualize
figure
hold on
plot(x_ex,v_ex,'-','LineWidth',1.7);
plot(x,v,'o','MarkerSize',10);
plot(xq,vq,'x','LineWidth',2.0,'MarkerSize',7);
hold off
grid on
title('Lagrange Interpolation');
xlabel('x');
ylabel('f');
図において, 丸が標本データ$v$, xが補間で得られた値$vq(:,1), vq(:,2), vq(:,3)$, 実践が1次, 2次及び3次のベッセル関数を示しています.
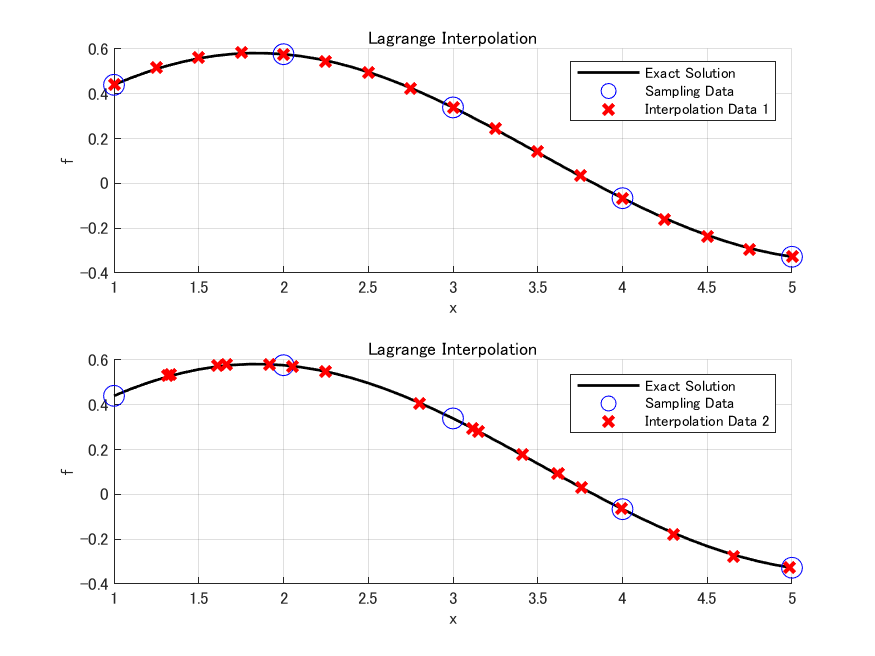
あるデータから複数の点の組み合わせでの補間
ここでは, 先ほどまでと同様に, $1 \leq x \leq 5$の範囲を等分割した列ベクトル$xq(:,1)$とランダムに同数の点を抽出した列ベクトル$xq(:,2)$を作成しました. そして, この2種類のベクトルの各点における補間した値$vq$を算出しました.
clear all; close all; clc;
%% Setting
start = 1;
stop = 5;
%% Get Multiple Interpolation Data from Single Sample
% Create Sampling Data
x = start:stop;
v = besselj(1,x);
% Exact Solution
x_ex = start:0.1:stop;
v_ex = besselj(1,x_ex);
% Interpolation
xq1 = start:0.25:stop;
xq2 = sort(start+(stop-start)*rand(1,length(xq1)));
xq = [xq1' xq2'];
vq = interpLag1(x,v,xq);
% Visualize
figure
subplot(2,1,1)
hold on
plot(x_ex,v_ex,'k-','LineWidth',1.3);
plot(x,v,'bo','MarkerSize',10);
plot(xq(:,1),vq(:,1),'rx','LineWidth',2.0,'MarkerSize',7);
hold off
grid on
title('Lagrange Interpolation');
xlabel('x');
ylabel('f');
legend("Exact Solution","Sampling Data","Interpolation Data 1");
subplot(2,1,2)
hold on
plot(x_ex,v_ex,'k-','LineWidth',1.3);
plot(x,v,'bo','MarkerSize',10);
plot(xq(:,2),vq(:,2),'rx','LineWidth',2.0,'MarkerSize',7);
hold off
grid on
title('Lagrange Interpolation');
xlabel('x');
ylabel('f');
legend("Exact Solution","Sampling Data","Interpolation Data 2");
図において, 上側は$1 \leq x \leq 5$を等分割した点での補間により得られた値$vq(:,1)$, 下側は$1 \leq x \leq 5$からランダムに抽出した点での補間により得られた値$vq(:,2)$を示している.
おわりに
今回は, 「$v$または$xq$の少なくとも一方がベクトルである」という仮定をつけてしまいましたが, 本家interp1ではn次元配列も使用することが可能です (難しかったので妥協してしまいました).
私を支えてくれている関数はまだまだたくさんあるので, 少しずつ備忘録として残しておこうと思います.
また, 今回は, 「MATLABにラグランジュ補間の関数がないなー」と思って作成しましたが, もしあれば教えていただきたいです!!
最後に, 本記事のアイデアをくださり, 一緒に考えてくれた方に, 心より感謝申し上げます.
参考文献
E. クライツィグ著, 田村義保訳, 技術者のための高等数学=5 数値解析 原書第8版, 培風館, 2015
MATLAB Documentation interp1