競プロではたまに使われますが、一般(?)にはあまり使われないかもしれない、多重ループを済ませる方法 について解説します。
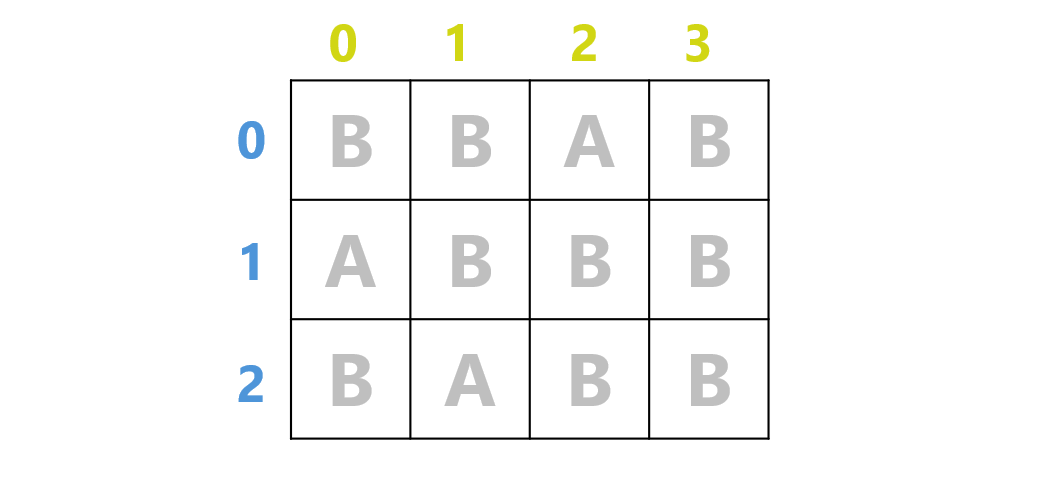
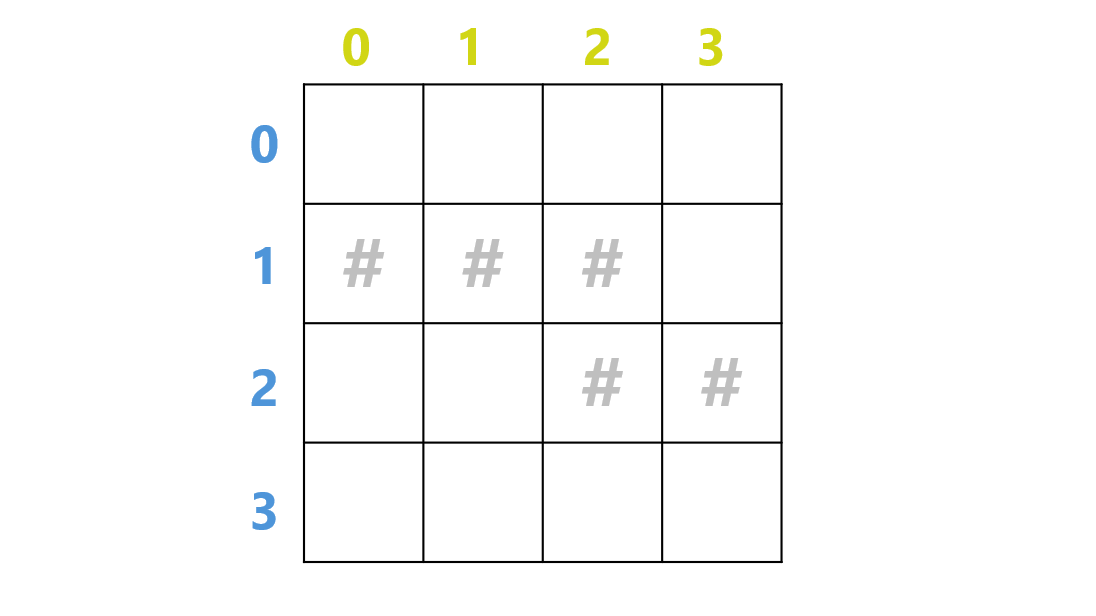
以上のような、A または B のいずれかの文字がかかれた、$3$ 行 $4$ 列のグリッドがあったとします。
「このグリッドに A がいくつあるか数えなさい」という問題を解く時、素朴に考えたら以下のようなコードになると思います。
grid = [
'BBAB',
'ABBB',
'BABB'
]
count = 0
for i in range(3):
for j in range(4):
if grid[i][j] == 'A':
count += 1
print(count) # 3
しかし、二重ループを書くとネストが深くなって見づらい、と思う方もいるかもしれません。
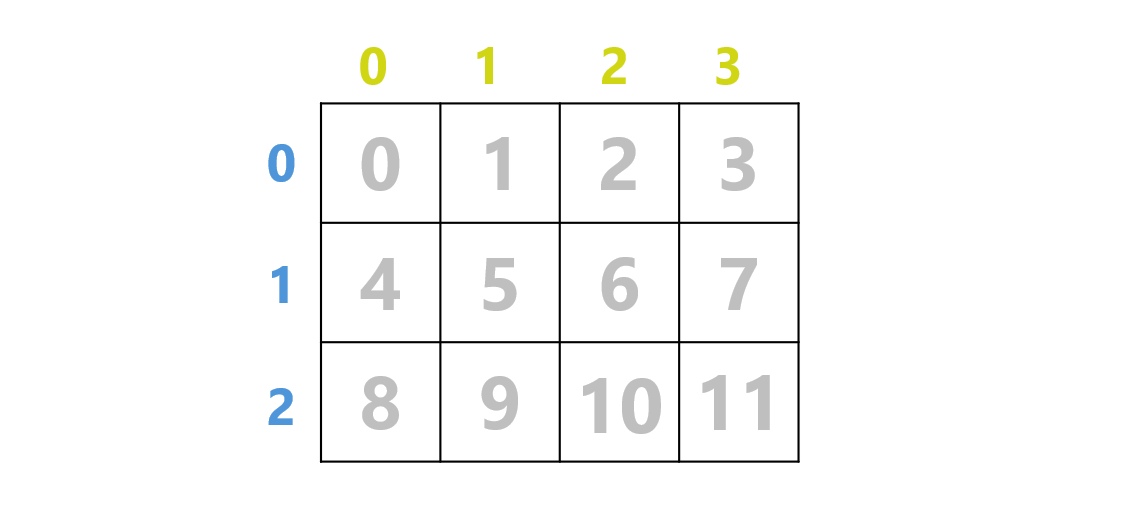
そこで、この二重ループを一次元で走査する方法を考えます。そのために、このグリッドに、以下のような通し番号を振ります。
この時、行番号、列番号、通し番号の関係は以下のようになっています。
\displaylines{
0 行 0 列 \Longleftrightarrow 通し番号 0 \\
0 行 1 列 \Longleftrightarrow 通し番号 1 \\
0 行 2 列 \Longleftrightarrow 通し番号 2 \\
0 行 3 列 \Longleftrightarrow 通し番号 3 \\
1 行 0 列 \Longleftrightarrow 通し番号 4 \\
\vdots \\
2 行 3 列 \Longleftrightarrow 通し番号 11 \\
}
実は、行番号は通し番号を 列数で割った商(繰り下げ)、列番号は通し番号を 列数で割ったあまり となっています。(なお、番号を $1$ から割り振った場合には、このような綺麗な対応にはなりません)
つまり、上のコードは以下のように書き換えられます。
count = 0
for i in range(3*4):
if grid[i//4][i%4] == 'A':
count += 1
print(count) # 3
これが、グリッドの二重ループを一次元で済ませる方法です。まあ、解説されるまでもなく直感的にわかるわい! という人も多いでしょうが、この方法のメリットとデメリットを考えてみます。
ネストが浅くなる
上にも述べた通り、ネストが浅くなります。既にネストが伸び切っていて、少しでも階層を節約したい場合には効果的かもしれません。ただし、ネストを浅くしたいなら関数に切り分けるのが一般的なマナーです。
変数名も節約できます。ただし、これも関数の切り分けと同じように、変数名が足らなくなったら、関数に切り分けるなり、構造体を作るなりして、名前空間を分けるのが一般的なマナーです。
以上のメリットは、自分だけがコードを解釈できればいい状況に限り、有効かもしれません。
余談ですが、いわゆる bit 全探索 は、$0\sim1$ の値を持つ $n$ 次元グリッドに対してこの手法を適用したものと考えることができます。
任意のグラフライブラリを適用できる
ダイクストラ法 や Union-Find のような、グラフ構造のための一般的なライブラリを、二次元グリッドに対して適用させたい場合、二次元座標を一次元座標に変換する必要があります。この場合、メリットというか、必然的に使わざるを得ないという感じですが。
なお、この方法を用いてグラフを探索する場合、エッジを張る際に実は 大きな罠 があるのですが、それは後程解説します。
多重ループをbreakできる
本記事で説明したい部分はここになります。私も最近気づきましたし、これに触れている解説記事が少ない(少し検索しただけだと見つからない)ので。
ループをまとめて抜け出したい
前提知識として、break の挙動について。これも、説明されなくとも知っている人がほとんどだと思いますが、一応……。
多重ループの中で break をした場合、脱出できるのは自分が 属するループ だけです。なので、冒頭にでてきたグリッド探索において、「A を発見したらその時点で打ち切る」というコードを書きたい場合、時々事故が起こります。
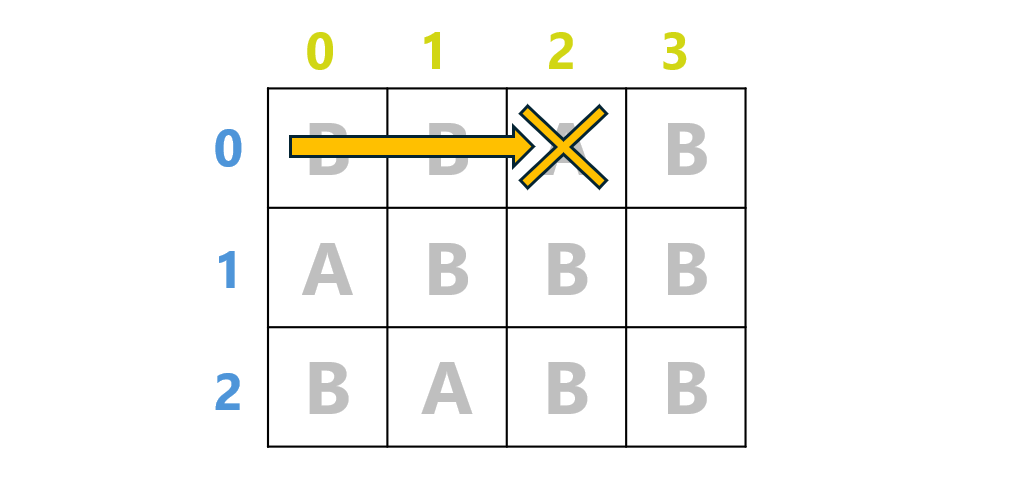
期待する挙動。
grid = [
'BBAB',
'ABBB',
'BABB'
]
for i in range(3):
for j in range(4):
print(f'grid({i},{j}) passed')
if grid[i][j] == 'A':
break
しかし、このコードの結果は以下のようになります。
grid(0,0) passed
grid(0,1) passed
grid(0,2) passed
grid(1,0) passed
grid(2,0) passed
grid(2,1) passed
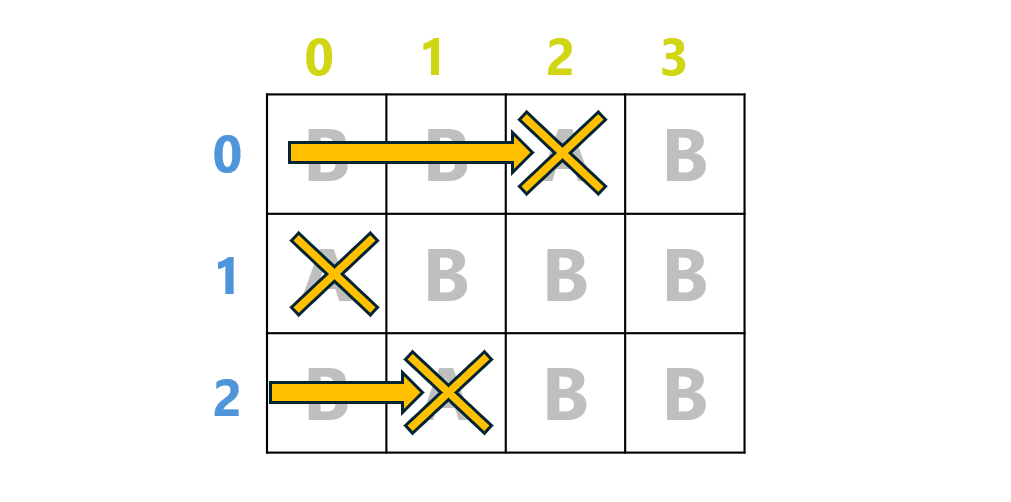
実際の結果はこうなっています。図を見るとその理由は一目瞭然だと思います。
つまり、打ち切るのは「列を探す」ことだけで、「行を探す」という部分は break されていないのです。
多重ループ脱出のために
多重ループ脱出のためには、例えば以下のような対策がなされます。
フラグ管理
成功フラグをつけて、それが ON ならばすぐに脱出するようにします。
okay = False
for i in range(3):
for j in range(4):
print(f'grid({i},{j}) passed')
if grid[i][j] == 'A':
okay = True
if okay:
break
if okay:
break
grid(0,0) passed
grid(0,1) passed
grid(0,2) passed
しかし、ループの数だけ if 文が必要になるので、冗長な感じがします。
関数化
関数として定義すれば、return が出た時点ですべての処理を打ち切るので、多重ループを強制終了することができます。
def main():
for i in range(3):
for j in range(4):
print(f'grid({i},{j}) passed')
if grid[i][j] == 'A':
return
main()
grid(0,0) passed
grid(0,1) passed
grid(0,2) passed
副作用と言えば、コードが関数で小分けになるので、人によってはそれを好まない人もいるかもしれません。とはいえ、「条件を満たすまで探して打ち切る」というロジックでコードを分離するのは、設計としても自然な発想です。多くの人にとって納得できる対策になると思います。
一次元化による対策
で、本題ですが、一次元化をすれば、この「多重ループの強制脱出」が実現できます。
for i in range(3*4):
print(f'grid({i//4},{i%4}) passed')
if grid[i//4][i%4] == 'A':
break
grid(0,0) passed
grid(0,1) passed
grid(0,2) passed
いちいちフラグ管理をしたり、関数化したりするのがわずらわしい時には、良いのではないでしょうか。
デメリット
この方法のデメリットを考えます。
可読性がやや下がる
慣れていない人にとっては面食らう形になります。特に、他人とコードを共有する時は気をつけた方がよいと思います。
また、自分だけが使うコードでも、ケアレスミスの危険が増えるかもしれません。
繰り上がりの罠
グリッド探索にもこれが適用可能だという話をしましたが、実はこれには罠があります。
$H$ 行 $W$ 列を持つグリッドにおいて、行内の移動は $-1,+1$、行間の移動は $-W,+W$ で簡潔に定義できます。これを用いれば、煩雑な BFS も簡潔に実装できる!
具体的な問題で考えてみましょう。上のグリッドにおいて、空白マスだけを通って $(0,0)$ から $(3,3)$ に到達できますかという問題を、BFS で解いていきます。正しい出力は、当然「不可能」です。
from collections import deque
h, w = (4, 4)
grid = ["....",
"###.",
"..##",
"...."]
q = deque()
dist = [-1] * h * w
q.append(0)
dist[0] = 0
while len(q):
now = q.popleft()
for move in [-1, 1, -w, w]:
next = now + move
if next < 0 or h * w <= next:
continue
if grid[next // w][next % w] == "#":
continue
if dist[next] != -1:
continue
dist[next] = dist[now] + 1
q.append(next)
if dist[h * w - 1] == -1:
print("No")
else:
print("Yes")
実はこの出力は Yes、つまり「可能」ということになります。
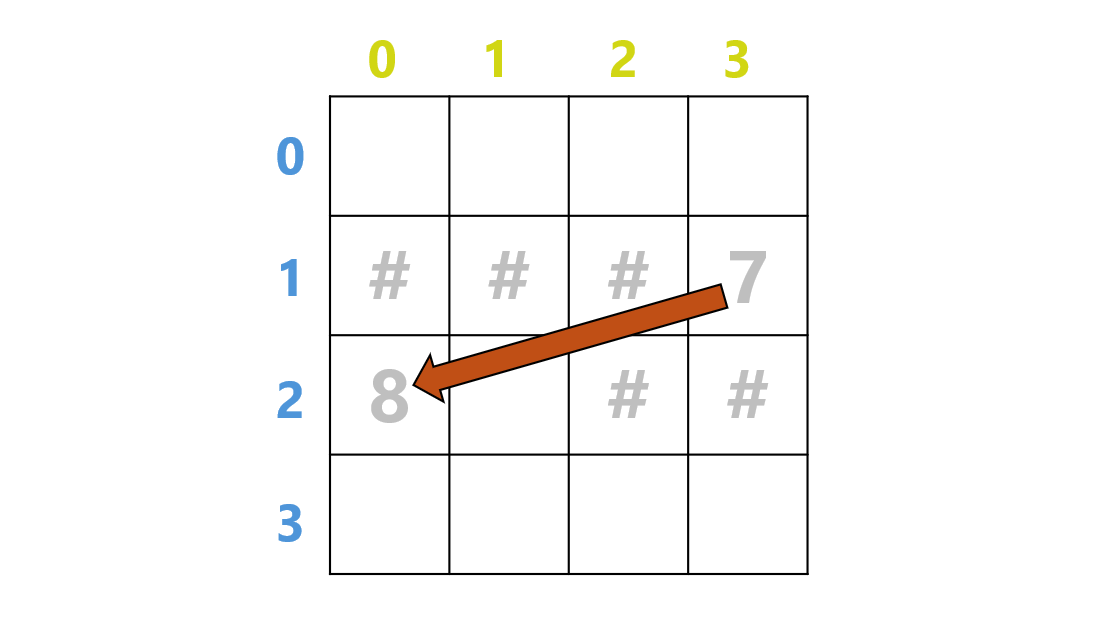
理由は、以下の図を見るとわかります。
通し番号 $7$ のマスから右に移動すると(本来これは不可能です)、$+1$ された通し番号 $8$ のマスに移動すると解釈されます。通し番号だと、このような「繰り上がり」が発生してしまうので、上下左右の移動の限界をチェックする際には二次元で考えないと思わぬバグを産んでしまうかもしれません。