なんとなく解説したくなったので。多分世界一詳しいと思います。
2点を打つ
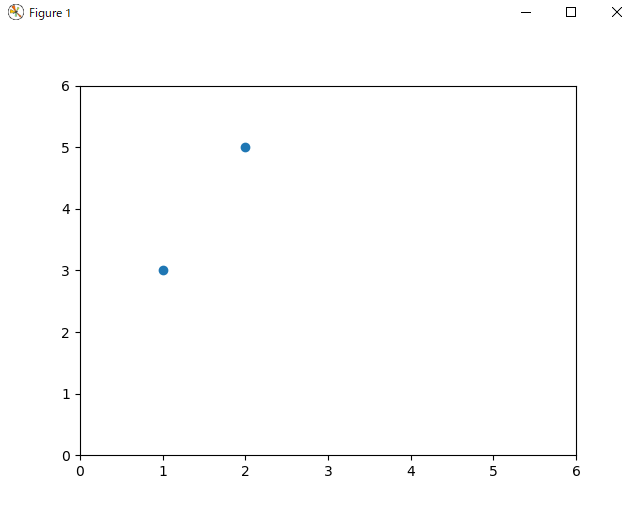
とりあえず点を打ちます。例として、$y=2x+1$ の関係を持つような点を 2 点打ちます。これが教師データになります。
import torch
from matplotlib import pyplot as plt
x = torch.Tensor([1, 2])
t = torch.Tensor([3, 5])
グラフにします。
plt.scatter(x, t)
plt.xlim((0, 6))
plt.ylim((0, 6))
plt.show()
適当にパラメータを決める
適当に決めます。これは実は都合の良いパラメータを選んでいたとかではなく、本当に適当でいいです。適当に $a=1,b=0$ とします。
a = torch.tensor(1., requires_grad=True)
b = torch.tensor(0., requires_grad=True)
requires_grad=Trueという謎の概念が出てきますが、これは勾配を持っていて欲しいということです。勾配が何かについては、ここでは詳しくは述べません。
勾配は、ここではまだ決定されていません。
print(a.grad, b.grad) # None None
予測する
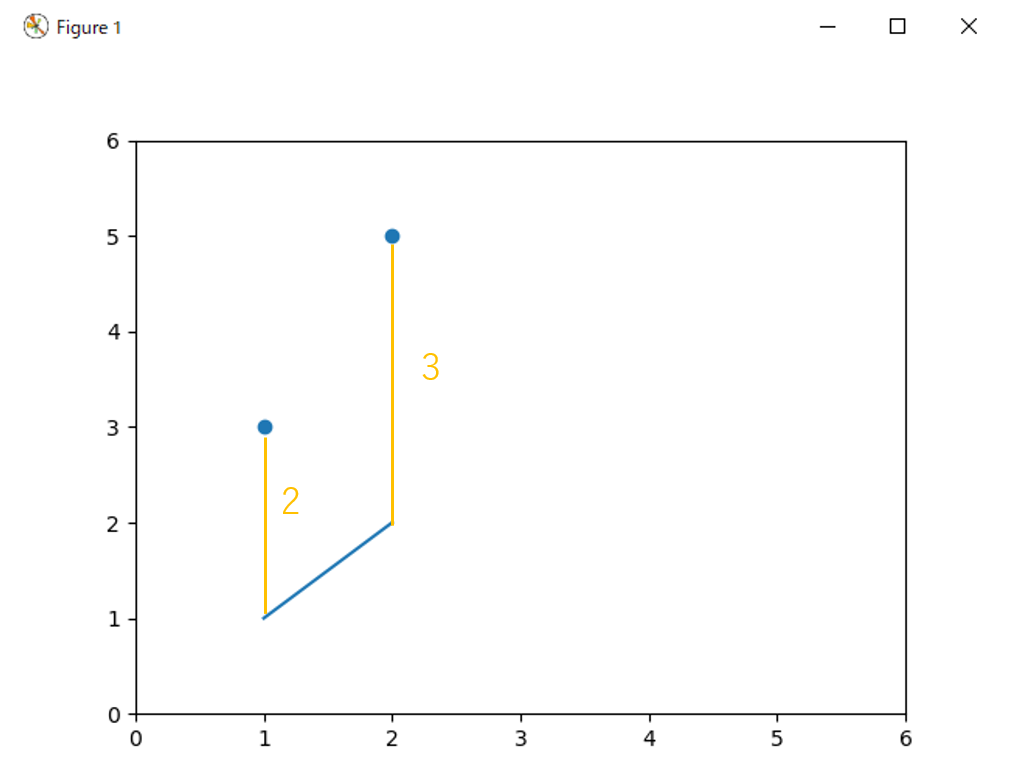
現在のa, bをもとに計算し、予測値をyとします。当然、正解の値とは異なるので全然違った数値になります。
y = a*x + b
plt.plot(x, y.detach())
plt.show()
detach()という謎の概念が出てきますが、これは先程つけた「勾配を持っていて欲しい」という情報をキャンセルしています。学習上の意図がある訳ではなく、pltに渡す時に勾配を持っているとエラーが出てしまうため、便宜上そうしているだけです。
グラフは以下のようになります。
それぞれ 2 と 3 も違います。どうにかしてこれを正解に近づけたい場合、いくつかの方法が考えられます。
- a を増やす
- b を増やす
- 同時に増やす
1. と 2. どちらかだけでは正解にたどり着けないので、3. を考えることになります。そこで、a と b が増えたら予測値がどれだけ増えるかを考えます。
a が 1 増えるとそれぞれの値は x だけ増えます。b が 1 増えるとそれぞれの値は 1 だけ増えます。これは、数学的には各々の偏微分を求めています。
誤差を出す
重要なのは予測値そのものではなく、予測値と教師データの誤差です。これを 0 にしたいです。
そこで、誤差 e を以下のように定めます。
e = (t - y)^2
いわゆるユークリッド距離(の 2 乗)です。素朴な感覚だと、直線距離(マンハッタン距離)
e = |t - y|
でもよさそうですが、こっちの方が何かと都合が良いです。二乗を誤差として使うので、MSE (Mean Squared Error) と呼ぶこともあります(伏線)。
誤差との予測
ユークリッド距離を使った結果、各パラメータと誤差の偏微分は以下のようになります。
\frac{\partial{e}}{\partial{a}} = 2(y - t)x \\
\frac{\partial{e}}{\partial{b}} = 2(y - t)
この結果、a と b をどれだけ増やしたら誤差を 0 にできそうか、という数値が計算されます。 実は PyTorch にはこれを自動で計算してくれる機能があります。
y = a*x + b
e = torch.mean((t - y)**2)
e.backward()
print(a.grad, b.grad) # tensor(-8.) tensor(-5.)
このbackwardが、機械学習で良く言われる誤差逆伝播の正体です。偏微分をつないだ結果、元の変数が増減したら誤差がどのように影響が出るかを計算したものです。グラフで説明するとこんな感じです。
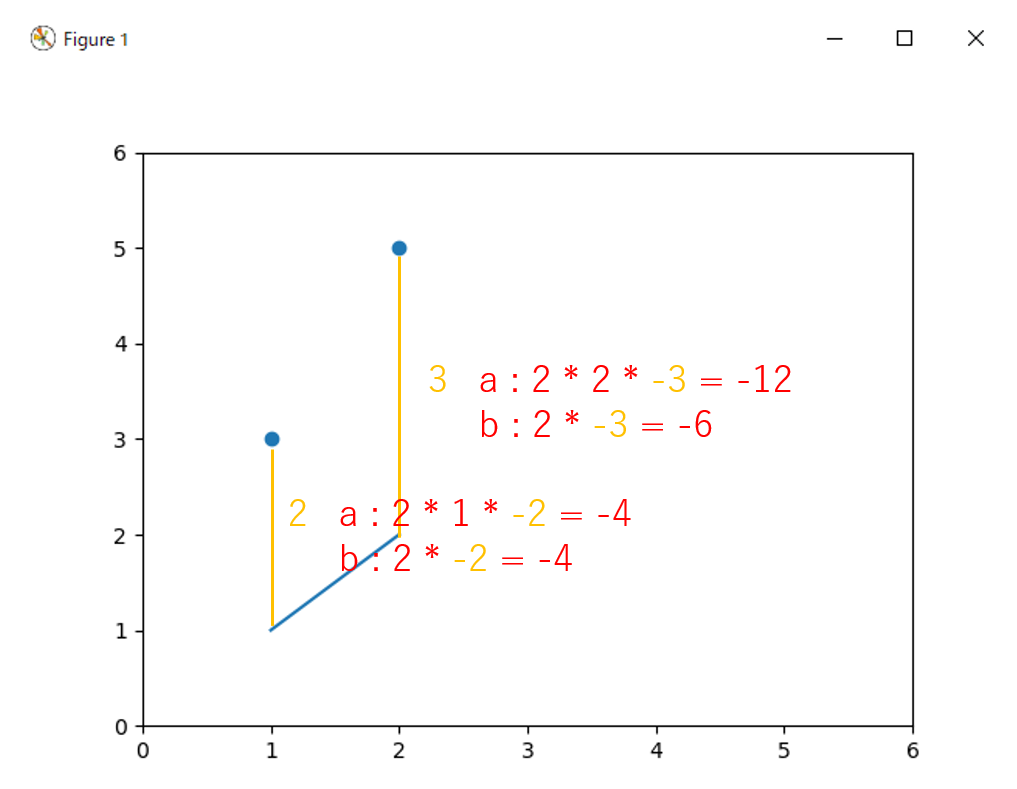
平均を取るので、a による誤差の勾配は $(-12-4)/2=-8$、b による誤差の勾配は $(-6-4)/2=-5$ です。
学習
この勾配を打ち消すような数値を加えれば理論上は誤差は 0 になる……とはならず、これらの勾配はそれ単体で誤差を 0 にする前提の値なので、これをそのまま加えるとオーバーランします。またこのようなシンプルな事例と違って、現実の数値は線形(同じような増減が永遠に続いていく)とは限りません。そのため、実際は誤差の打ち消しを軽減するような補正を加えます。これを学習率と言います。今回は0.1とします。
a = (a - a.grad * 0.1).detach().requires_grad_()
b = (b - b.grad * 0.1).detach().requires_grad_()
a と b に修正を加えます。後ろについているdetach().requires_grad_()は、一旦勾配を削除した後、また初期化した勾配をセットしたものです。PyTorch の数値データ(勾配付きテンソル)は、計算を加えるために、内部に偏微分をかけたものを勾配として保持する仕様になっているため、同じ計算を繰り返すと勾配が蓄積されてしまいます。なので、逐一リセットする必要があります。
上の修正の結果、a とb は以下のようになります。
print(a, b) # tensor(1.8000, requires_grad=True) tensor(0.5000, requires_grad=True)
a が$1.0 - (-8/10) = 1.8$、bが $0.0 - (-5/10) = 0.5$ になっていることがわかります。
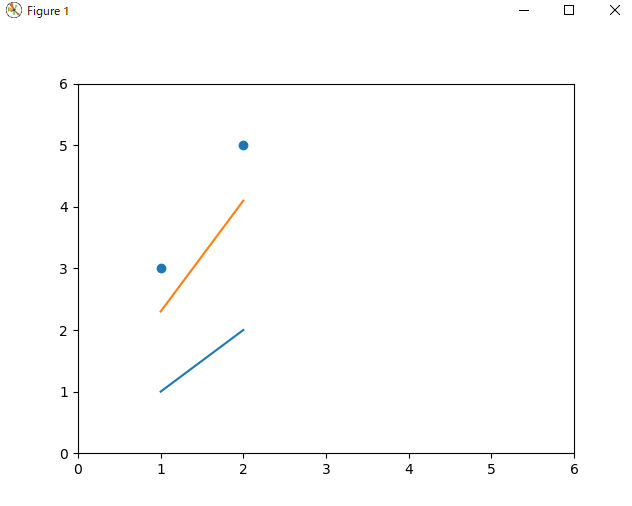
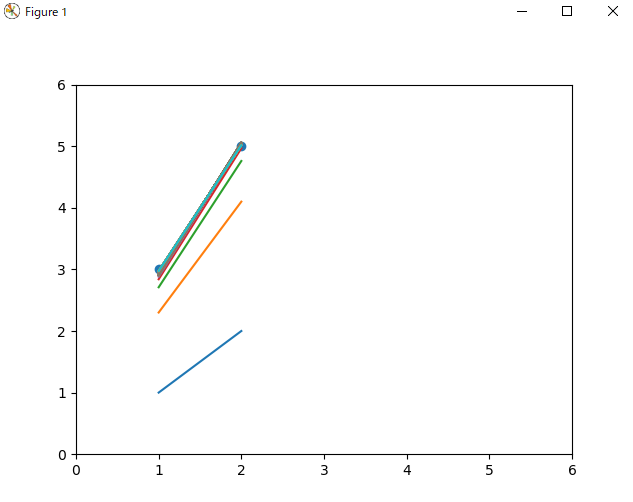
グラフもかなり近づいています。いわゆる「学習」とは、このようなパラメータの修正を言います。
同じ作業を 100 回行ってみます。
for i in range(100):
y = a*x + b
plt.plot(x, y.detach())
e = torch.mean((t - y)**2)
e.backward()
print(a.grad, b.grad)
a = (a - a.grad * 0.1).detach().requires_grad_()
b = (b - b.grad * 0.1).detach().requires_grad_()
print(a, b) # tensor(2.0393, requires_grad=True) tensor(0.9364, requires_grad=True)
$a=2,b=1$ にほぼ近い結果が得られました。学習率を下げ、反復回数を上げれば、もちろん精度は上がります。
ソースコード
今までの操作のソースコードをまとめます。
import torch
from matplotlib import pyplot as plt
x = torch.Tensor([1, 2])
t = torch.Tensor([3, 5])
# print(x, t)
plt.scatter(x, t)
plt.xlim((0, 6))
plt.ylim((0, 6))
# plt.show()
a = torch.tensor(1., requires_grad=True)
b = torch.tensor(0., requires_grad=True)
for i in range(100):
y = a*x + b
plt.plot(x, y.detach())
e = torch.mean((t - y)**2)
e.backward()
a = (a - a.grad * 0.1).detach().requires_grad_()
b = (b - b.grad * 0.1).detach().requires_grad_()
print(a, b)
plt.show()
よくある書き方
今まで学習の仕組みと、その具体的な計算を解説しました。同じ内容を、PyTorch のチュートリアルで良くみるような書き方で書いてみます。
import torch
from torch import nn, optim
from matplotlib import pyplot as plt
x = torch.Tensor([1, 2]).reshape(2,1)
t = torch.Tensor([3, 5]).reshape(2,1)
plt.scatter(x, t)
plt.xlim((0, 6))
plt.ylim((0, 6))
net = nn.Sequential(
nn.Linear(1,1)
)
optimizer = optim.SGD(net.parameters(),lr=0.1) # 学習方法と学習率の設定
for i in range(10):
y = net(x)
plt.plot(x, y.detach())
loss = nn.MSELoss()(t,y) # 二乗による誤差の指定
loss.backward() # 誤差逆伝播
optimizer.step() # 学習
optimizer.zero_grad() # 勾配の初期化
plt.show()
初期パラメータは乱数になっていますが、やっていることは今まで説明した内容と全く同じです。
よくある書き方その2
Sequential ではなくクラスを定義する方法。
import torch
from torch import nn, optim
from matplotlib import pyplot as plt
x = torch.Tensor([1, 2]).reshape(2,1)
t = torch.Tensor([3, 5]).reshape(2,1)
plt.scatter(x, t)
plt.xlim((0, 6))
plt.ylim((0, 6))
class Net(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(1,1)
def forward(self, x):
x = self.linear(x)
return x
net = Net()
optimizer = optim.SGD(net.parameters(),lr=0.1) # 学習方法と学習率の設定
for i in range(10):
y = net(x)
print(y)
plt.plot(x, y.detach())
loss = nn.MSELoss()(t,y)
loss.backward() # 誤差逆伝播
optimizer.step() # 学習
optimizer.zero_grad() # 勾配の初期化
plt.show()
感想
この記事が機械学習や PyTorch を学ぶ人の導入の助けになれば幸いです。
お世話になったサイト
PyTorchは誤差逆伝播とパラメータ更新をどうやって行っているのか?...テンソルや勾配の扱い方についてかなり参考になりました。