クォータニオン（四元数）を使って自前でLookAtを実装したらダイナミックになった話

　先日、趣味のプログラムで「任意の位置に対して、常に自分の方を見てくれるカメラ」を作るためにatan2などを用いて実装しました。経度方向・緯度方向の2方向に分けてオイラー角を出したのですが、

• 2ステップ必要
• 緯度が90度のときに例外処理が必要（経度を定義できないので）

　という点であまりスマートではないので、噂の四元数（クォータニオン）を使えばそのあたりを鮮やかに解決できるのではないかと思い、試してみました。プログラムはPythonで書きましたが、四元数の実装や挙動の検証にはUnityが便利なので、以下Unityで行います。

LookAt

　そもそもUnityには「ある方向を見る」という便利な関数が用意されています。もしUnityだけで完結するアプリなら、これを使うのが一番便利でしょう。以下のような実質1行のスクリプトで実装できます。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class LookAtFunction : MonoBehaviour
{
    public GameObject targetObject;

    void Start()
    {
    }

    void Update()
    {
        transform.LookAt(targetObject.transform.position);
    }
}

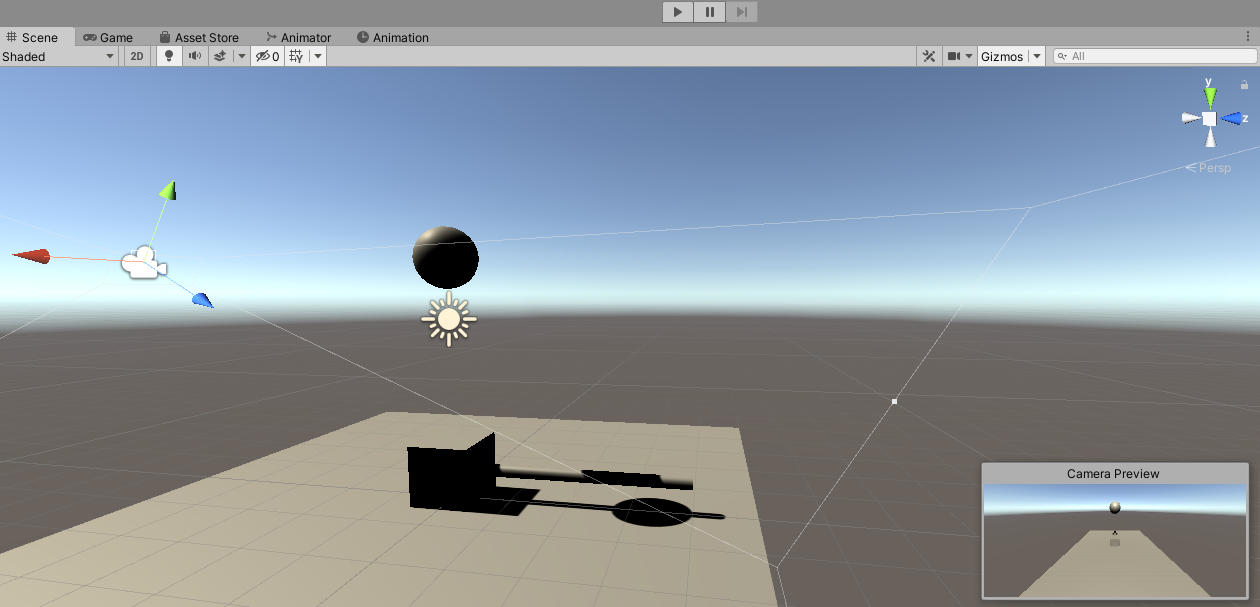
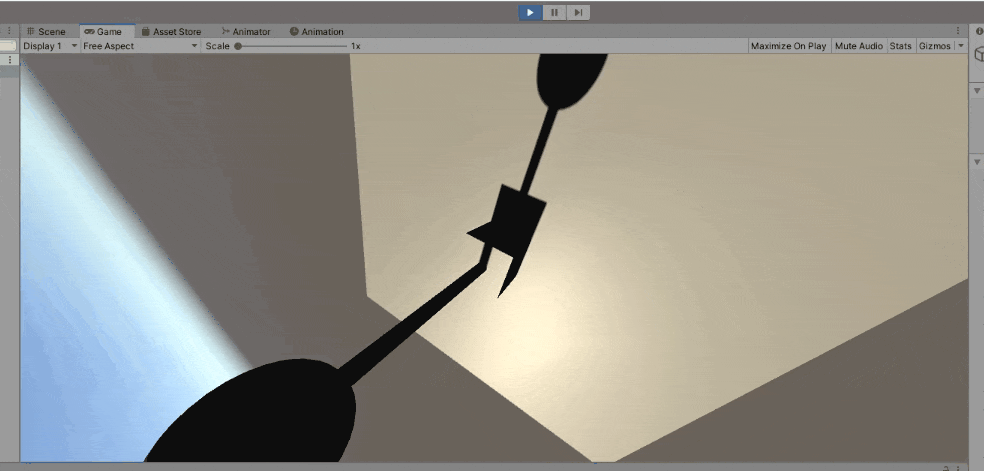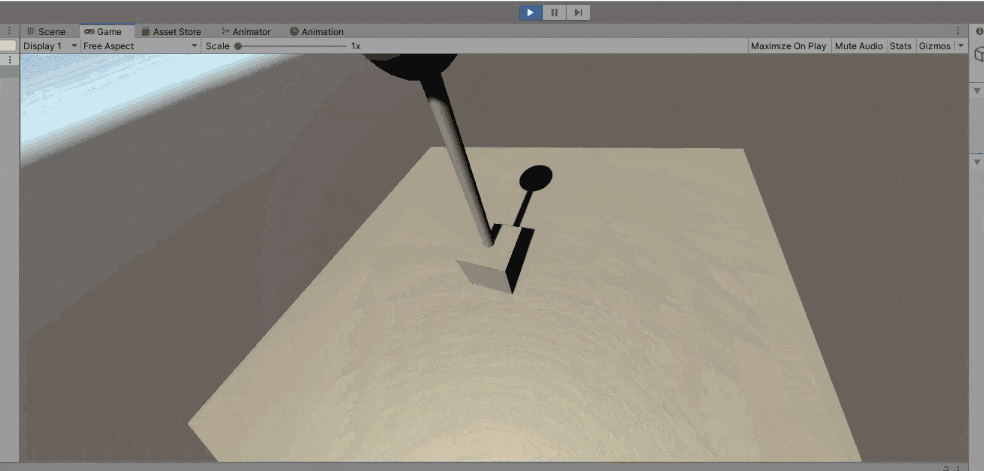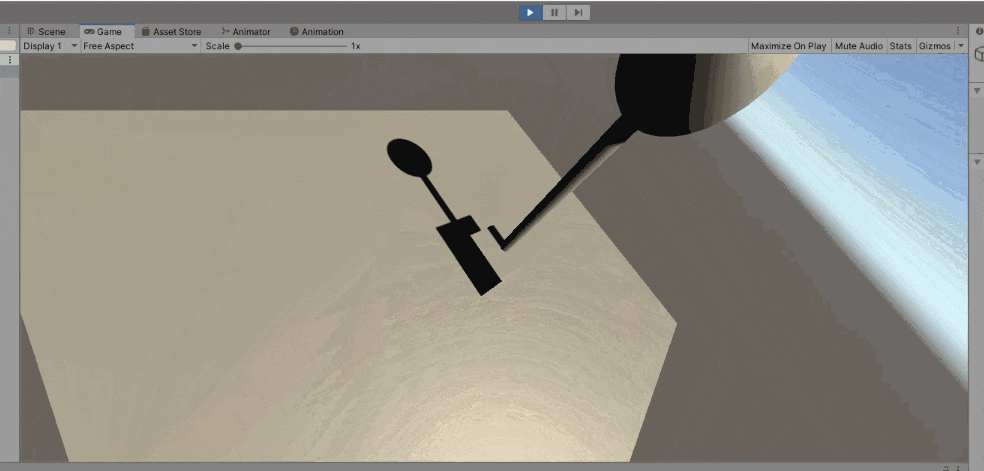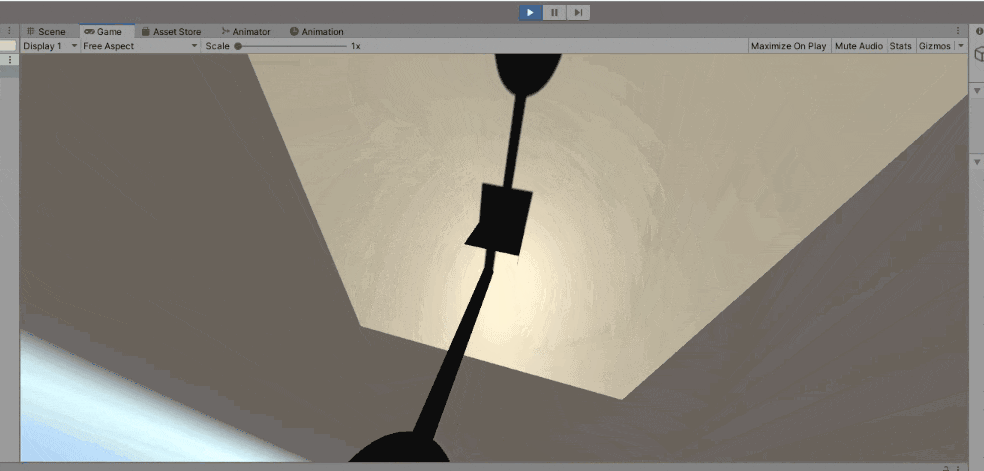
　Unityを使って簡単な検証を行います。Cylinderを子に持ったCubeに上のスクリプトを貼り付けて、円運動を行うSphereをtargetObjectにします。

LookRotation

　せっかくなのでもう少し四元数ぽいことをしてみます。Quaternion.LookRotation()という関数があり、これはベクトルを引数としてそのベクトルの方向をQuaternionとして変換してくれるという便利機能です。これを算出し、transformのrotationにこれを代入するという方向でLookAtの代用としてみましょう。関数頼りであることには変わりませんが。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class LookAtRotation : MonoBehaviour
{
    public GameObject targetObject;

    void Start()
    {
    }

    void Update()
    {
        Vector3 target = targetObject.transform.position - transform.position;
        Quaternion look = Quaternion.LookRotation(target);
        transform.rotation = look;
    }
}

　検証結果は上の動画と同じになるため割愛します。

自前で実装

　本題です。以上のような便利関数に頼らなくても四元数を直接計算してLookAtの機能を代入できないでしょうか？

　クォータニオンは軸ベクトルと回転角を指定することにより回転を定義します。であれば、いま見ている方向と対象に向かう方向を含むような平面において、両者のなす角度だけ回転させれば、対象に向かう方向を見ていることになります。

　伝える気ゼロの図で恐縮ですが、赤がデフォルトで見ている方向、青が対象の方向、緑が両者を含むような平面上における回転軸、ということになります。

　この回転軸は、両ベクトルの外積を取ることにより計算できます。また、この場合における「デフォルトで見ている方向」とは(0,0,1)になります（※Unityはx,y,zの左手座標系であり、前後方向はz）。そして両ベクトルの角度は、正規化（長さを1に揃えた）された状態での内積に${cos}^{-1}$をかけることにより計算できます。

　以上を実装します。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class LookAtQuartenion : MonoBehaviour
{
    public GameObject targetObject;

    void Start()
    {
    }

    void Update()
    {
        Vector3 target = targetObject.transform.position - transform.position; //対象の方向
        target = target.normalized; //正規化
        Vector3 norm = new Vector3(0, 0, 1); //デフォルトの方向
        float dot = Vector3.Dot(norm,target); //内積
        float theta = Mathf.Acos(dot);　//角度の算出
        Vector3 cross = Vector3.Cross(norm, target); //外積

　あとはcrossを軸にtheta分だけ回せばよいです。ここでもQuaternion.AngleAxisという便利関数があって、軸と角度を指定してくれればそれに応じたQuaternionを返してくれますが、それには頼らず自前で実装しましょう。
　
　四元数のそれぞれの値は、

x=u_x sin\frac{\theta}{2}\\
y=u_y sin\frac{\theta}{2}\\
z=u_z sin\frac{\theta}{2}\\
w = cos\frac{\theta}{2}

　で計算できます。ここで$u$は軸となるベクトルです。外積で得られたベクトルを正規化したものがそれになります。実装します。

        //上のコードの続き 
        cross = cross.normalized;
        theta = theta / 2;
        q.x = cross.x * Mathf.Sin(theta);
        q.y = cross.y * Mathf.Sin(theta);
        q.z = cross.z * Mathf.Sin(theta);
        q.w = Mathf.Cos(theta);
        transform.rotation = q;
    }
}

　以下が検証です。

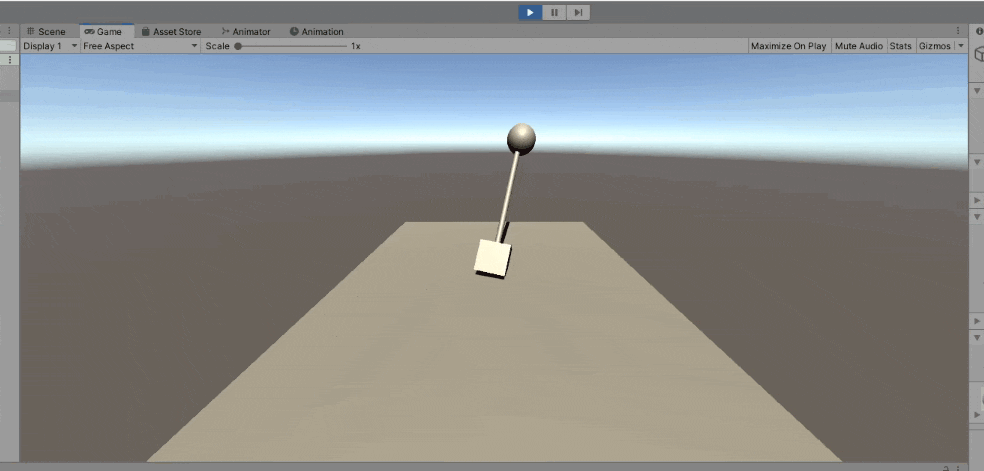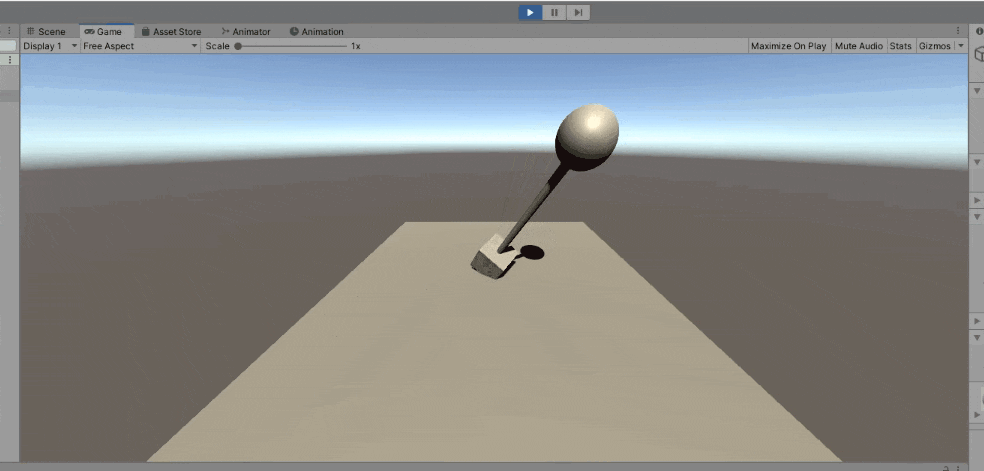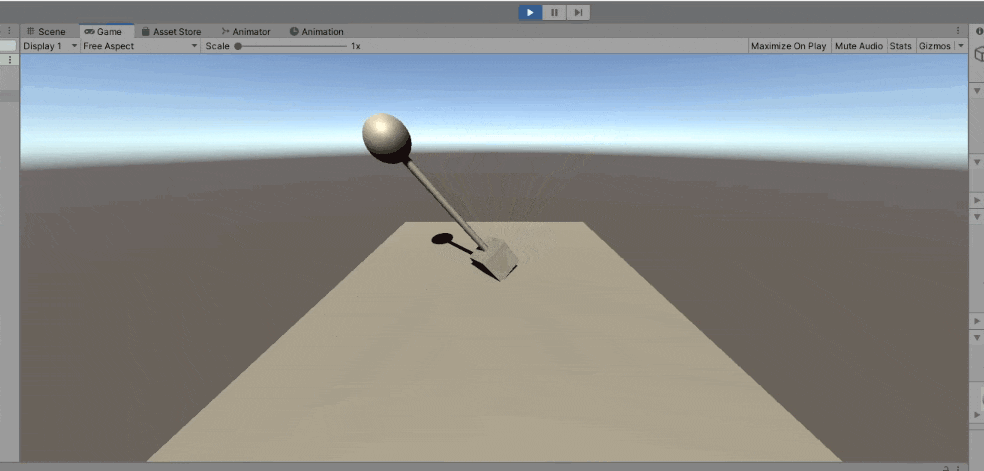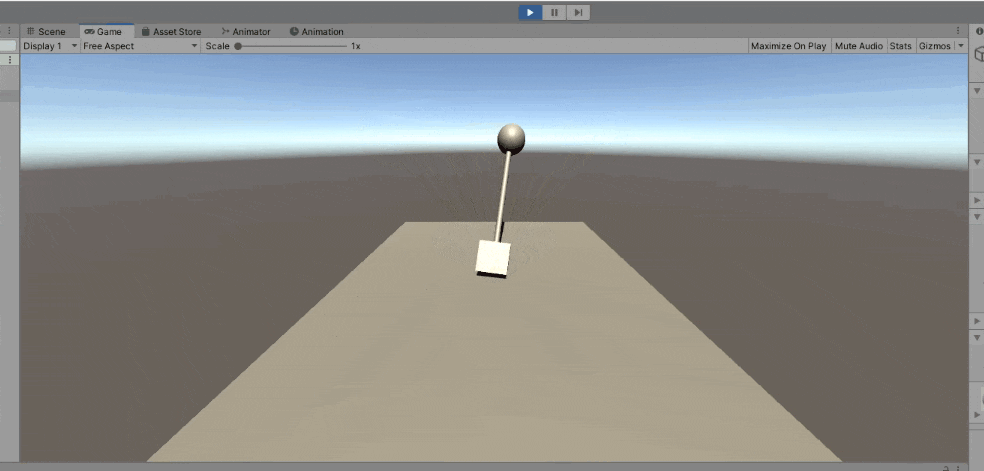
　勝ちました！　四元数に勝ちました！

#しかし……

　しかし、上の動画をよく見てみると、Sphereの方向を向いてはいますが微妙に角度がねじれていることがわかります。ここで最初の目的である「常に自分を見続けるカメラ」に戻って、LookAtを使った効果と比較してみます。今度はカメラが動きます。

　LookAtを使ったもの↓

　自前で実装したもの↓

　えらいダイナミックになっています。確かに中心を向いてはくれていますが……。

まとめ

　言われてみれば$(0,0,1)$から最短経路で対象を向いてくれている気はしますが、自然な角度になるとは限らないということですね。やはりLookAtやLookRotationを使った方がよさそうです。しかし、他の関数を一切使わずに内積と外積の計算だけでこういった機能を実装できるのは面白いですね。四元数サイコー。今回実装したダイナミックLook関数のソースコード全文は以下になります。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class LookAtQuaternion : MonoBehaviour
{
    public GameObject targetObject;
    void Start()
    {
    }
    void Update()
    {
        Vector3 target = targetObject.transform.position - transform.position;
        target = target.normalized;
        Vector3 norm = new Vector3(0, 0, 1);
        float dot = Vector3.Dot(norm,target);
        float theta = Mathf.Acos(dot);
        Vector3 cross = Vector3.Cross(norm, target);
        Quaternion q;
        cross = cross.normalized;
        theta = theta / 2;
        q.x = cross.x * Mathf.Sin(theta);
        q.y = cross.y * Mathf.Sin(theta);
        q.z = cross.z * Mathf.Sin(theta);
        q.w = Mathf.Cos(theta);
        transform.rotation = q;
    }
}