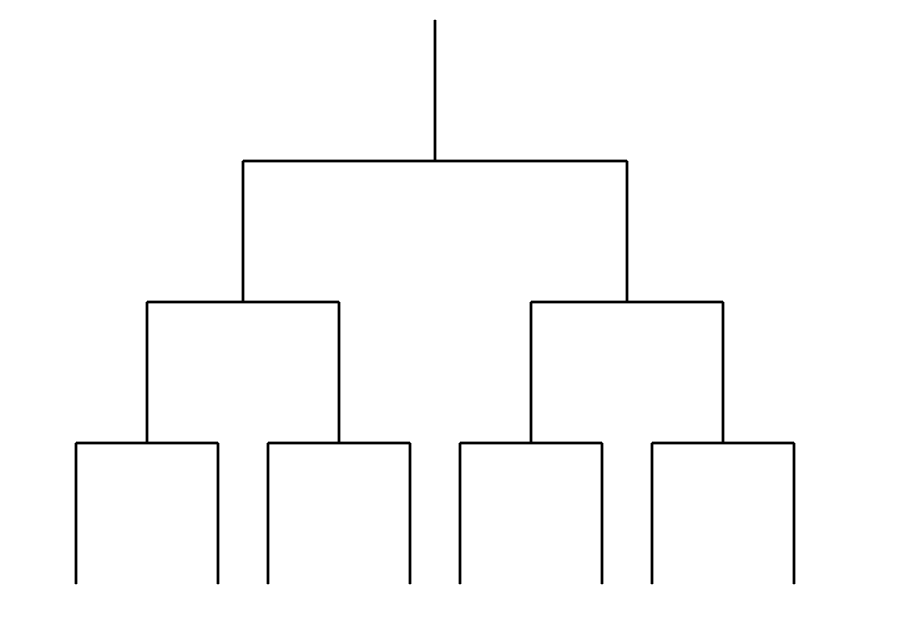
ダブルエリミネーション方式トーナメント
先日、ダブルエリミネーション方式のトーナメントに参加する機会がありましたが、これってわかりづらいですよね。初見で理解できる人はなかなかいないと思います。また、試合回数について正確に書いてある記事も少ないので、そのあたりについて考えてみることにしました。
シングルエリミネーション
まず、普通の勝ち残り式トーナメントから考えていきたいと思います。これは馴染み深いので説明不要かと思います。
非常にわかりやすく盛り上がりやすいですが、運の要素が大きく(最初に強い人と当たったら初戦敗退!)、また一度負けるともう大会に参加できないので、わりと理不尽感が強いです。エンターテイメント要素が強く求められる場合、また参加者の日程を確保するのが難しい場合に適しているといえるでしょう。
総試合ステップ
$n$人が参加するとして、全ての試合を行うのに何ステップかかるのかを計算します。最初の試合日程では全員が戦えますが、それで半分が離脱するので、次の試合日程ではその半分しか戦えません。その次は……ということを繰り返していくと、総試合日程は$\log_2 n$回になります。4人だったら2回、8人だったら3回、16人だったら4回です。
総試合数
1回戦うごとに1人抜けていくのだから、$n$人から1人を残すためには$(n-1)$試合戦う必要があります。4人だったら3試合、8人だったら7試合、16人だったら15試合です。
決定順位
決勝戦を行うことによって1位と2位は決定できますが、それ未満はベスト4ということまでしか決まっていないので、もし3位を決めたい場合は3位決定戦を行う必要があります。この場合、必要は試合数は$n$回になります。なお、あまりないと思いますが8位までの順位を詳細に決めようと思ったら、更に3回の試合が必要になります。
ダブルエリミネーション

(引用:Wikipedia)
ここからやっとダブルエリミネーションの話に入ります。シングルエリミネーションでは1回負けたらそれっきりだったので運の要素が大きかったですが、それでは理不尽すぎるということで、1回までなら負けてもOK、2回負けたらアウト、ということにしたのがダブルエリミネーション方式になります。1度負けた人は敗者ラウンド(Loser Round)という別のトーナメントに回されます。そこでは普通の勝ち抜き(シングルエリミネーション)を行います。その敗者ラウンドで勝ち抜いた敗者チャンピオンが、勝者ラウンドで最後まで残っていた勝者チャンピオンと戦います。
そこまで一発勝負でもなく、かといってリーグ戦よりは順位争いをしている感が出る、合理的な方式かと思われます。ややこしいですけど。
総試合ステップ
試合の流れはこんな感じになります。赤く塗ったのが WR(勝者ラウンド)、青く塗ったのが LR(敗者ラウンド)です。WR のチャンピオンと LR のチャンピオンが戦うのが GF(グランドファイナル)です。敗者チャンピオンは既に1回負けているので、ここで負けたら敗退です。しかし勝者チャンピオンは今まで無敗できているので、この試合に負けて敗退するとなると、1回しか負けていないのに敗退することになってしまいます。不公平ですね。なので、勝者側が負けた場合は再戦することができます。このあたりのダブルエリミネーションの複雑なところですね。
試合の流れに着目します。WR と LR の人数が一致してからは、2回の試合を行うとちょうどそれぞれの人数が半分になることがわかります。
- 最初は全員が WR で試合を行う。その後、WR と LR に均等に分かれる
- 2回試合するごとに参加人数が半分になる
- 2人になった時点で GF。試合数は1~2。
という風に整理すると、総試合ステップは
\displaylines{
1+2(\log_2 n-1)+G \\
2 \log_2 n - 1 + G \\
(G=1,2)
}
となります。4人だったら4回か5回、8人だったら6回か7回、16人だったら8回か9回です。4人ならもう総当り戦やれよとは思いますが、まあ思考実験です。
総試合数
上にも述べた通り、総試合数は GF の展開によって変化します。
- 勝者チャンピオンがストレート勝ちした場合…$2n-2$試合
- そうでない場合…$2n-1$試合
決定順位
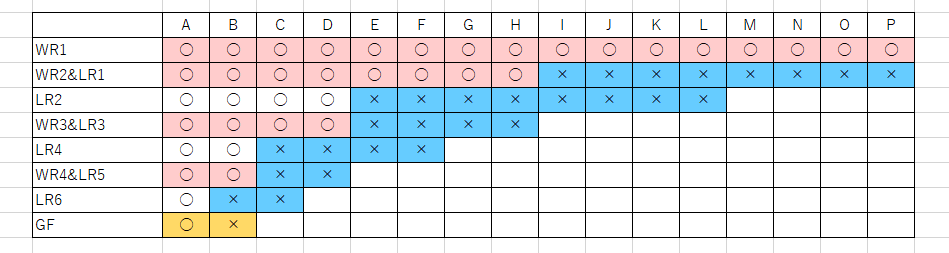
LR で負けた時点で順位が決定します。上の16人の例で言えば、
- LR1 で負けた時点でベスト16
- LR2 で負けた時点でベスト12
- LR3 で負けた時点でベスト8
- LR4 で負けた時点でベスト6
- LR5 で負けた時点で4位
- LR6 で負けた時点で3位
- GF で負けた時点で2位
となります。4位までは追加で順位決定線を行わなくても大丈夫です。
トリプルエリミネーション
ダブルエリミネーションでさえややこしいのに、トリプルなんて! もう総当り戦かスイスドローでいいだろ! と思いますが、一応実例はあるようです。この場合は WR と LR の間にもう1つラウンドが必要になります。仮に MR(中間ラウンド)とでも名付けておきましょう。下の表では緑色にしています。
総試合ステップ
真面目に見る必要はあまりないと思います。次節の表を見るとわかりやすいですが、敗者チャンピオンと中間チャンピオンの決勝(表では SF と表記)と GF には3回~5回の試合数が必要です。数字にすると、
\displaylines{
4+3(\log_2 n-2) + G \\
3\log_2 n - 2 + G
}
となります。4人なら7~9試合、8人なら10~12試合、16人なら13回~15試合です。
総試合数
誰か1人を除いて×を埋めるには、最短3回、最長5回の試合が必要です。という訳で総試合数は$3n-3$ ~ $3n-1$です。
決定順位
6位までは決定されます。
m回エリミネーション
ちょっと一般化してみましょう。総試合数は表から容易に推測されるように、$mn-m$ ~ $mn-1$回ですが(勝者は$0$ ~ $m-1$回負けられるため)総ステップ数はちょっとややこしいです。参加者を$m$個のラウンドに均等に割り振られるまでに何ステップ必要か、また、その時に各ラウンドに何人残っているかを一般化するのが複雑そうで、今回は断念しています。しかしそれを一般化できたとして、その知識が何かに役立つことはないでしょう。