　UnityPackageはこちらから。

　任意の画像を変形させて一次変換や固有ベクトルを可視化するシェーダを作成しました。ソースコードは載せますが、数学成分多めな記事です。

　一次変換やら固有ベクトルやら、言葉で説明してもわかりづらいと思うので、画像で説明すると、

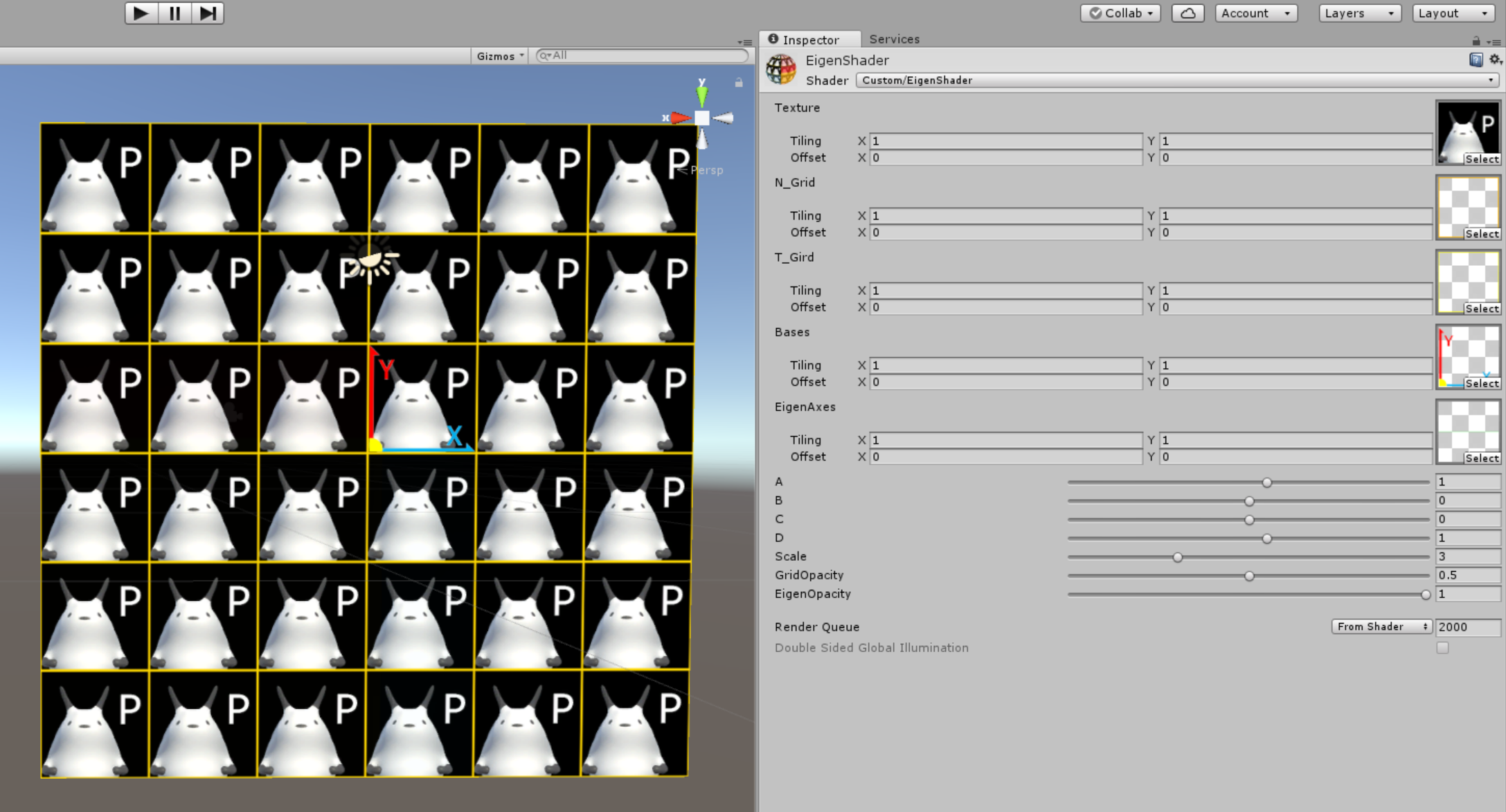
　これが、

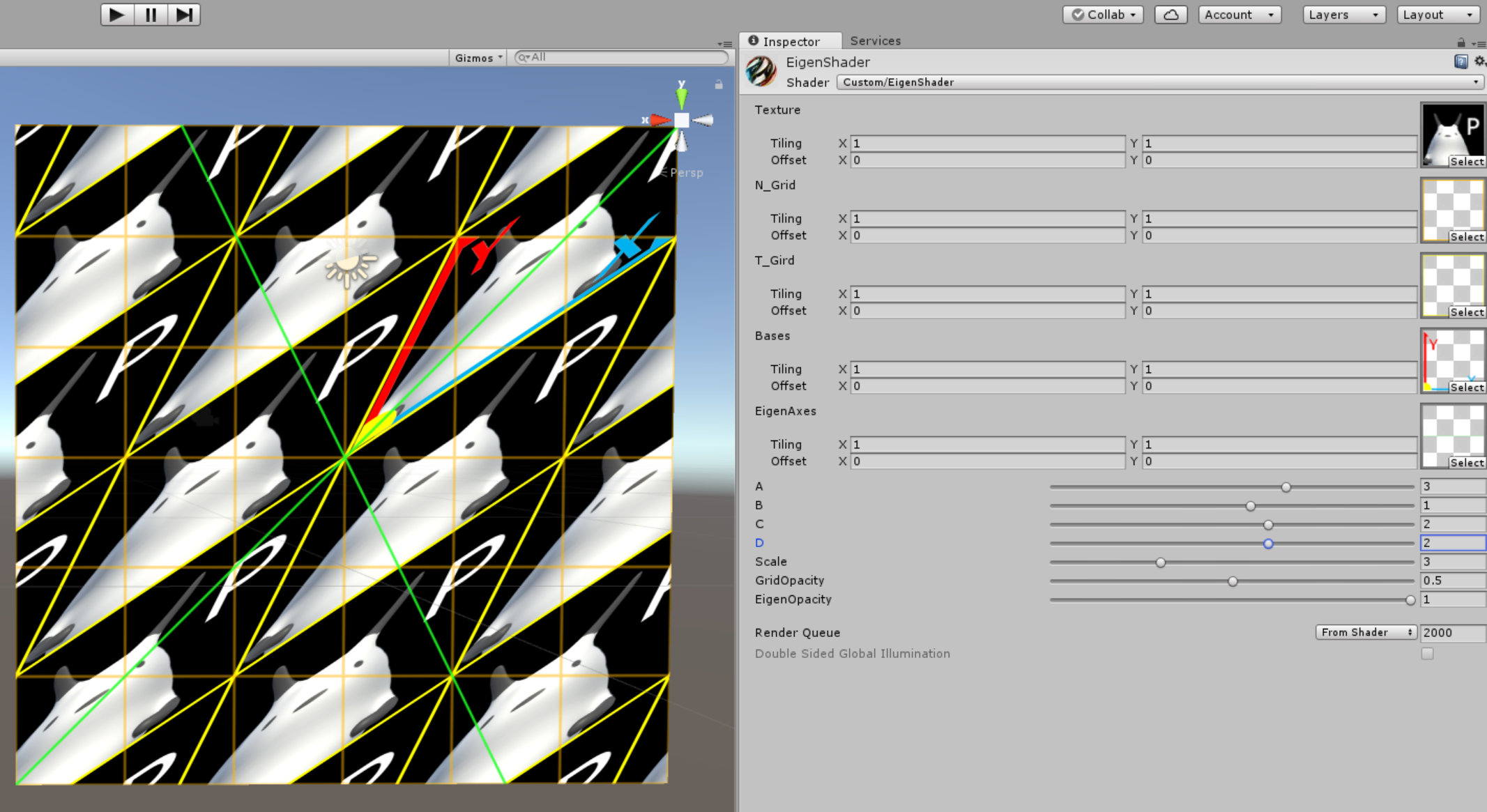
　こうなったり、

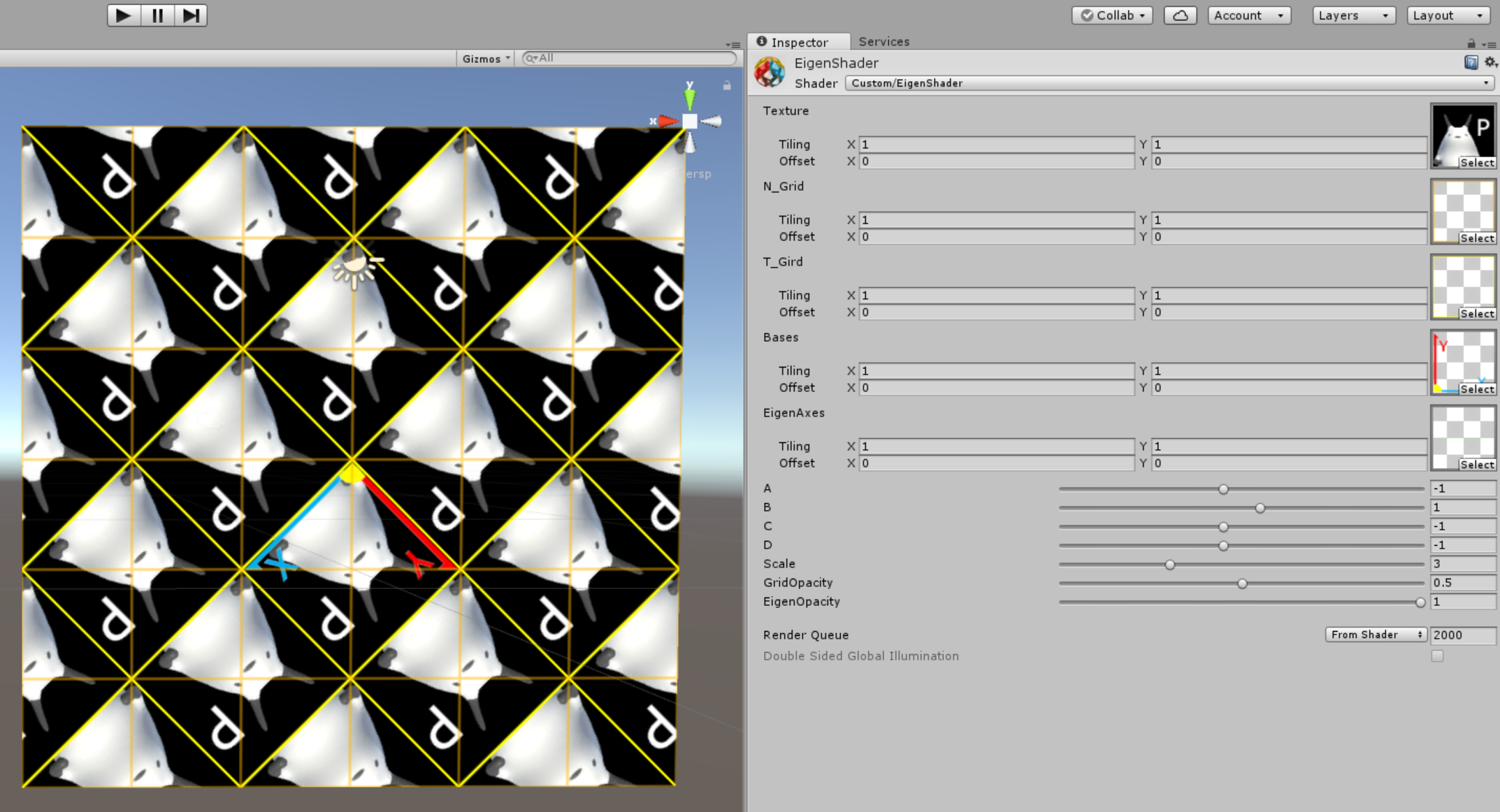
　こうなったりします。緑色の線は固有ベクトルの軸を示しています。なお、このパンダのような生命体は私のオリジナルアバターです。もちろん、任意のテクスチャを入れれば、それが変形されます。

ソースコード

　とりあえずソース見せろという方へ。

Shader "Custom/EigenShader"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _N_Grid("N_Grid", 2D) = "white"{}
        _T_Grid("T_Gird", 2D) = "white"{}
        _Bases("Bases", 2D) = "white"{}
        _EigenAxes("EigenAxes", 2D) = "white"{}
        _A("A",Range(-10,10)) = 0
        _B("B",Range(-10,10)) = 0
        _C("C",Range(-10,10)) = 0
        _D("D",Range(-10,10)) = 0
        _Scale("Scale",Range(0,10)) = 5
        _GridOpacity("GridOpacity",Range(0,1)) = 0
        _EigenOpacity("EigenOpacity",Range(0,1)) = 0
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            sampler2D _MainTex;
            sampler2D _T_Grid;
            sampler2D _N_Grid;
            sampler2D _Bases;
            sampler2D _EigenAxes;
            float _A;
            float _B;
            float _C;
            float _D;
            float _Scale;
            float _GridOpacity;
            float _EigenOpacity;
            float4 _MainTex_ST;

            v2f vert (appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                UNITY_TRANSFER_FOG(o,o.vertex);
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                float2 xy = float2(i.uv.x,i.uv.y);
                xy -= .5;
                float lambda1 = (_A+_D)/2+sqrt(pow(_A-_D,2)+4*_B*_C)/2;
                float lambda2 = (_A+_D)/2-sqrt(pow(_A-_D,2)+4*_B*_C)/2;
                float theta1 = atan2(lambda1-_A,_B);
                float theta2 = atan2(lambda2-_A,_B);
                theta1 = atan2(_C,lambda1-_D);
                theta2 = atan2(_C,lambda2-_D);
                float2x2 eigenrot1 = float2x2(cos(theta1),sin(theta1),-sin(theta1),cos(theta1));
                float2x2 eigenrot2 = float2x2(cos(theta2),sin(theta2),-sin(theta2),cos(theta2));
                float2 eigenxy1 = mul(eigenrot1,xy);
                half4 c5 = tex2D(_EigenAxes,eigenxy1+.5);
                float2 eigenxy2 = mul(eigenrot2,xy);
                half4 c6 = tex2D(_EigenAxes,eigenxy2+.5);
                float det = _A*_D-_B*_C;
                float2x2 trans = float2x2(_D,-_B,-_C,_A);
                xy =_Scale*2*xy;
                half4 c4 = tex2D(_N_Grid,xy);
                xy = mul(trans,xy)/det;
                fixed4 c = tex2D(_MainTex, xy);
                half4 c2 = tex2D(_T_Grid, xy);
                half4 c3 = tex2D(_Bases, xy);
                if (pow(_A-_D,2)+4*_B*_C < 0) {
                    _EigenOpacity = 0;
                }
                c.rgb = lerp(c.rgb, c2.rgb, c2.a);
                c.rgb = lerp(c.rgb, c3.rgb, c3.a);
                c.rgb = lerp(c.rgb, c4.rgb, c4.a*_GridOpacity);
                c.rgb = lerp(c.rgb, c5.rgb, c5.a*_EigenOpacity);    
                c.rgb = lerp(c.rgb, c6.rgb, c6.a*_EigenOpacity);
                return c;
            }
            ENDCG
        }
    }
}

なにがしたいか

　よくある平凡なx,y座標に、一次変換の行列

A=\begin{pmatrix}
a & b \\
c & d 
\end{pmatrix}

　を作用させた場合、元々のx軸、y軸、図形がどのように変形されるかを見るためのものです。変形については、適当な図形（円、文字）を貼りつけるよりも、画像をまるごと貼りつけるのが一番わかりやすいです。例示としてパンダ（のようなもの）の画像をつかったのはそのためです（一応、方向の変換がわかりやすいようにPの字をつけたりしています……）。

　元々の基底（格子の目の単位となるベクトル）については、

A\times\vec{e_x} =\begin{pmatrix}
a & b \\
c & d 
\end{pmatrix}
\times\
\begin{pmatrix}
1 \\
0 
\end{pmatrix}
=
\begin{pmatrix}
a \\
c 
\end{pmatrix}\\
A\times\vec{e_y} =\begin{pmatrix}
a & b \\
c & d 
\end{pmatrix}
\times\
\begin{pmatrix}
0 \\
1 
\end{pmatrix}
=
\begin{pmatrix}
b \\
d 
\end{pmatrix}

　となります。つまり、変形後は（a,c）がx'軸（＝新しいx軸）、（b,d）がy'軸（＝新しいy軸）となります。

　上の画像は、

A=\begin{pmatrix}
3 & 1 \\
2 & 2 
\end{pmatrix}

　の場合ですが、x'軸が（3,2）、y'軸が（1,2）になっているのがわかると思います。

シェーダ上の実装

　これをシェーダに実装します。uv座標に行列Aを作用させればそれでいいのではないか……と言うと違います。uv座標は基底にあたるので、例えばuv座標の値を2倍すると、描画される結果は1/2に縮んで見えます。それと同じで、uv座標にはAではなく$A^{-1}$を作用させる必要があります。

\begin{pmatrix}
a & b \\
c & d 
\end{pmatrix}
^{-1}=\frac{1}{ad-bc}\begin{pmatrix}
d & -b \\
-c & a 
\end{pmatrix}

　これをuv座標に作用させます。コードで言うと、

                float det = _A*_D-_B*_C;
                float2x2 trans = float2x2(_D,-_B,-_C,_A);
                xy =_Scale*2*xy;
                half4 c4 = tex2D(_N_Grid,xy);
                xy = mul(trans,xy)/det;

　の部分がそうです。transが逆行列、mul(trans,xy)/detがそれを作用させてる部分になります。

固有ベクトルの導出

　ここから先は独自色の強い説明になりますが、ご容赦ください。

　次の大きな目的は「固有ベクトルを可視化したい」というものになります。固有ベクトルとは、線形変換において「変形の中心」（厳密なたとえではないですが、イメージとして）のようなものです。そのベクトルは変換後であろうが方向が変わりません。そのようなベクトルを固有ベクトルと言い、ニ次行列では2つ存在します（ない場合もあります）。これが何の役に立つかというと、行列の対角化によって計算を簡略化できたり、主成分分析によって多次元の情報を集約できたりするのですが、ここでは詳細を述べません。変形によって歪んでしまった座標の中にあって、有用な情報を取り出すための「核」のようなものであると、少なくとも私はそう考えています。

　能書きはともかく計算ですね。まずは固有値を出しましょう。

\begin{pmatrix}
a & b \\
c & d 
\end{pmatrix}\times\vec{x}=\lambda\times\vec{x}\\
\begin{pmatrix}
a-\lambda & b \\
c & d-\lambda 
\end{pmatrix}\times\vec{x} = 0

　これが恒等的に成り立つためには、左辺の行列の行列式が0である必要があります。

det \begin{pmatrix}
a-\lambda & b \\
c & d-\lambda 
\end{pmatrix}=(a-\lambda)(d-\lambda)-b\cdot c=0\\
\lambda = \frac{a+d}{2}\pm\frac{\sqrt{(a-d)^2+4bc}}{2}

　なんだかスッキリしない形ですが、とりあえずこれが二次行列に対する固有値の一般式になります。（ところで、この一般式はネットをざっと探しても見つからなかったのですが、マジでないんですかね？）
　あとはこれをもとに固有ベクトルを出します。固有ベクトルはある傾きのベクトルの集合（つまり直線）なので、候補は無数にあるのですが、代表として$\vec{x}=(1,t)$とおくと、tがベクトルの傾きになるので便利です。

\begin{pmatrix}
a-\lambda & b \\
c & d-\lambda 
\end{pmatrix}\times
\begin{pmatrix}
1 \\
t 
\end{pmatrix}=0\\
t=(-1)\cdot\frac{a-\lambda}{b}=\frac{\lambda-a}{b}

　なお、$(a-\lambda):b=c:(d-\lambda)$より、$t=(-1)\cdot\frac{c}{d-\lambda}=\frac{c}{\lambda-d}$でもありますが、どちらを用いても同じなので、計算は前者の値を使うことにします。

　$\frac{\lambda-a}{b}$はそのまま固有ベクトルの傾きになるので、$tan^{-1}$によりその角度を出すことができます。2つの固有値$\lambda_1,\lambda_2$について、それぞれの角度を回転させて固有ベクトル（というか直線）を出します。コードで言うと、

                float lambda1 = (_A+_D)/2+sqrt(pow(_A-_D,2)+4*_B*_C)/2;
                float lambda2 = (_A+_D)/2-sqrt(pow(_A-_D,2)+4*_B*_C)/2;
                float theta1 = atan2(lambda1-_A,_B);
                float theta2 = atan2(lambda2-_A,_B);
                theta1 = atan2(_C,lambda1-_D);
                theta2 = atan2(_C,lambda2-_D);
                float2x2 eigenrot1 = float2x2(cos(theta1),sin(theta1),-sin(theta1),cos(theta1));
                float2x2 eigenrot2 = float2x2(cos(theta2),sin(theta2),-sin(theta2),cos(theta2));
                float2 eigenxy1 = mul(eigenrot1,xy);
                half4 c5 = tex2D(_EigenAxes,eigenxy1+.5);
                float2 eigenxy2 = mul(eigenrot2,xy);
                half4 c6 = tex2D(_EigenAxes,eigenxy2+.5);

　の部分です。

　なお、固有値に実数解が存在しない場合は固有ベクトルが存在しないので、その時は表示しません。これは後の、

                if (pow(_A-_D,2)+4*_B*_C < 0) {
                    _EigenOpacity = 0;
                }

　でそういう制御をしています。Opacityは不透明度の意味で、合成する時のアルファ値にする変数です。これを0にすることにより非表示しています。

　さて、固有ベクトルについて具体例を出します。

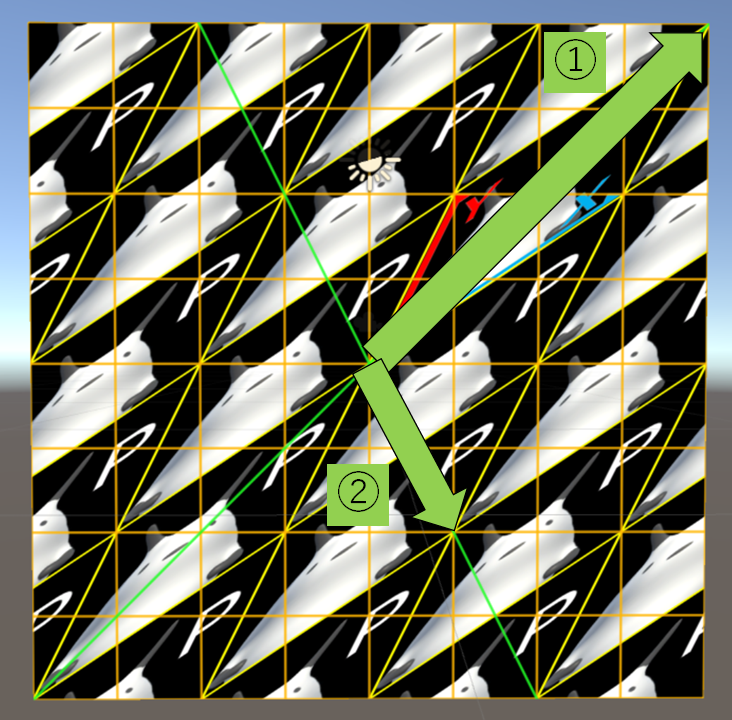
　先程とおなじく

A=\begin{pmatrix}
3 & 1 \\
2 & 2 
\end{pmatrix}

　の場合ですが、この時の固有ベクトルは（1,1）と（1,-2）を含む、それらを延長した直線になります。対応する固有値はそれぞれ4と1です。例えば、

x'y'上での（1,1）がxy上での（1,1）の4倍になっていること
x'y'上での（1,-2）がxy上での（1,-2）の1倍になっていること

　がわかると思います。

コードの補足

　やたらプロパティが多くてすいません。

    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _N_Grid("N_Grid", 2D) = "white"{}
        _T_Grid("T_Gird", 2D) = "white"{}
        _Bases("Bases", 2D) = "white"{}
        _EigenAxes("EigenAxes", 2D) = "white"{}
        _A("A",Range(-10,10)) = 0
        _B("B",Range(-10,10)) = 0
        _C("C",Range(-10,10)) = 0
        _D("D",Range(-10,10)) = 0
        _Scale("Scale",Range(0,10)) = 5
        _GridOpacity("GridOpacity",Range(0,1)) = 0
        _EigenOpacity("EigenOpacity",Range(0,1)) = 0
    }

　それぞれ解説します。

Texture　変形させたい画像です。図だとパンダです。
N_Grid　Non-transformed Gridの略です。変形前の格子目です。図だとオレンジです。
T_Grid　Transformed Gridの略です。変形後の格子目です。図だと黄色です。
Bases　基底（Bases）です。図だと青と赤で記されたXとYの矢印です。
EigenAxes　固有ベクトル（を伸ばした軸）です。図だと緑色です。
A,B,C,D　二次行列の成分です。
Scale　マス目の表示範囲です。4だったらx=4まで表示します。
GridOpacity　変形前の格子目の不透明度です。非表示にしたい時は0にします。
EigenOpacity　固有ベクトル（を伸ばした軸）の不透明度です。非表示にしたい時は0にします。

　先頭にも貼りましたが、テクスチャ画像も含んだUnityPackageを配布しております。

一次変換と固有ベクトルを可視化するシェーダ

ソースコード

なにがしたいか

シェーダ上の実装

固有ベクトルの導出

コードの補足