しゃくとり法ではqueueを使おう委員会（C++編）

　皆さんしゃくとり法（尺取り法）は好きですか？ 私は嫌いです。なぜならバグらせやすいからです。二分探索で代替できるならすべて二分探索で行いたい。lとrの動きがイメージできない。半開区間の扱いを間違える。しかしqueueを使うことで「今lとrはどの位置にいるのか？」を考えることなく実装できます。私の主張に賛成する方は、今から一緒に世の中にqueueしゃくとり法を啓蒙していきましょう。

　この方が言うべきことはすべて言ってくれているのですが、実装がPythonなので、C++でも例題を交えて解説していきたいと思います。

　なお、尺取り中の列（いわゆるlとrに挟まれた部分）だけでなく、元となる列もqueueで実装することができます。なんと、2つのqueueを制御するだけで、添字を一切登場させずにしゃくとり法を実装することができるのです。（前者の列は要素を一列になめていくだけなので、vectorを使ってもほぼ同じことは当然できるのですが）

例1

筆者の提出

　この問題を例に解説していきます。

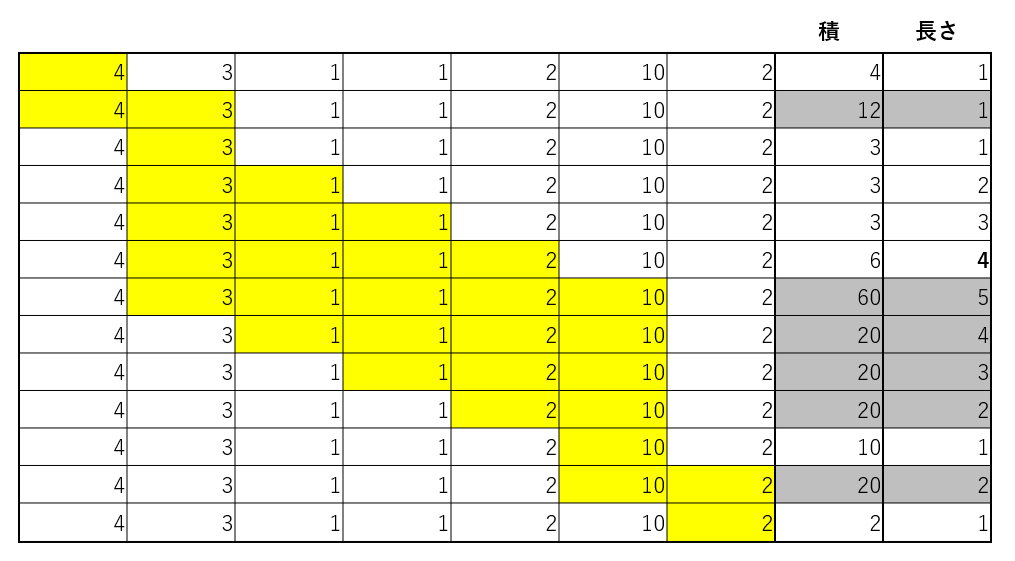
　4 3 1 1 2 10 2 という数列から、積が 6 以下になる最大の長さはどれだけ取れるかという問題です。正解は 3 1 1 2 の長さ 4 です。

　正統派な尺取り法では以下のように考えます。

　とりあえず右に伸ばして、積が6を超えた時点で左に縮める、という処理を繰り返します。

　これはqueueを2つ用いることで以下のように実装もできます。（インクルードやマクロは省略）

int main() {
  int n, k;
  cin >> n >> k;
  bool check_zero = false;
  //元となるキューpと、尺取り中の列q
  queue<int> p, q;
  rep(i, n) {
    int s;
    cin >> s;
    if (s == 0) {//この問題では0を含む場合のコーナーケースが必要
      check_zero = true;
    }
    p.push(s);
  }
  if (check_zero) {
    cout << p.size() << endl;
    return 0;
  }
  int ans = 0;
  //基準となる処理（尺取り中の列の積は？）
  ll criterion = 1;
  while (p.size() > 0) {
    int now = p.front();
    p.pop();
    q.push(now);
    criterion *= now;
    //次の数を入れていい状態になるまでqを整理
    while (criterion > k && q.size() > 0) {
      int rm = q.front();
      q.pop();
      criterion /= rm;
    }
    ans = max(ans, int(q.size()));
  }
  cout << ans << endl;
}

　重要なのはwhile以下の部分です。この時pやqはどのような動きを辿っているのでしょうか。ちょっとデバッグしてみます。

p : 3 1 1 2 10 2
q : 4
criterion : 4
p : 1 1 2 10 2
q : 4 3
criterion : 12
p : 1 1 2 10 2
q : 3
criterion : 3
p : 1 2 10 2
q : 3 1
criterion : 3
p : 2 10 2
q : 3 1 1
criterion : 3
p : 10 2
q : 3 1 1 2
criterion : 6
p : 2
q : 3 1 1 2 10
criterion : 60
p : 2
q : 1 1 2 10
criterion : 20
p : 2
q : 1 2 10
criterion : 20
p : 2
q : 2 10
criterion : 20
p : 2
q : 10
criterion : 10
p : 2
q :
criterion : 1
p :
q : 2
criterion : 2

　添字を全く使えず、whileとpushとpopを繰り返すだけで、上の図と全く同じ処理ができていることがわかります。また、この手法では、qのメンバ変数が使えますので、qの長さや末尾等にも添字を意識することなく簡単にアクセスできます。これによって、要らぬバグを踏む可能性は大幅に減ります。

例2

筆者の提出

　例えば、1 2 3 2 1 の中に単調増加となる部分列はいくつあるかという問題です。単調増加となるブロックに分けて、それの長さをnとするとn*(n+1)/2を足し続ければよいです。（1~n の順番を問わない2つの組合せなので）

int main() {
  int n;
  cin >> n;
  //元となるキューpと、尺取り中の列q
  queue<int> p, q;
  rep(i, n) {
    int a;
    cin >> a;
    p.push(a);
  }
  p.push(0); //この問題では末尾に番兵を入れる
  ll ans = 0;
  //この問題では基準処理に新たな変数は必要ない
  while (p.size() > 0) {
    int now = p.front();
    p.pop();
    //次の数を入れていい状態になるまでqを整理
    if (q.size() > 0) {
      if (q.back() >= now) {
        ll len = q.size();
        ans += len * (len + 1) / 2;
        while (q.size() > 0) {
          q.pop();
        }
      }
    }
    q.push(now);
  }
  cout << ans << endl;
}

　p.front()とq.back()を使うことで添字を使うことなく条件の比較ができます。

例3

筆者の提出

　例えば 1 2 1 3 1 4 4 の中で同じ数字を含まない数列の最大の長さはいくつかという問題です。条件が少し複雑ですが、qの中にその数がすでにあるか？　ということをvector<bool>で管理すれば効率的に処理できます。

int main() {
  int n;
  cin >> n;
  //元となるキューpと、尺取り中の列q
  queue<int> p,q;
  rep(i,n){
    int a;
    cin >> a;
    p.push(a);
  }
  int ans = 0;
  //基準となる処理（既にqにその数は含まれているか？）
  vector<bool> criterion(1e5 + 1);
  while(p.size()>0){
    int now = p.front();
    p.pop();
    //次の数を入れていい状態になるまでqを整理
    while (criterion[now]) {
      int rm = q.front();
      q.pop();
      criterion[rm] = false;
    }
    q.push(now);
    criterion[now] = true;
    ans = max(ans, (int)q.size());
  }
  cout << ans << endl;
}

結論

　queueを使えばしゃくとり法もこわくない！