K番目の数を決め打ち二分探索で求めたいときのチートシート

非本質な部分に関する説明を省くため、本記事に出てくる数字はすべて正の整数であるものとします

　ある配列（ナイーブに扱うと超巨大）において$K$ 番目に小さい数を求めよ、みたいなときに 決め打ち二分探索 をおこなうことはよくあります。

結論

　長さ $N$ の配列において、

• $K$ 番目に小さい数は、「$X$ 以下となるような数が $K$ 個以上となるような最小の $X$ 」
• $K$ 番目に大きい数は、「$X$ 超過となるような数が $K$ 個未満となるような最小の $X$」
  • または、「$X$ 以下となるような数が $N-K+1$ 個以上となるような最小の $X$」

　ほかにも色々言い換えはありますが、これが一番バグを踏むおそれが少ないです（と思います）。
　理由は後述します。

理論的背景

「小さい方から」の場合

　アルゴロジック 様が、競技プログラミングで解法を思いつくための典型的な考え方 において、「小さい方から」の場合について端的にまとめてくださっているので、それを引用します。

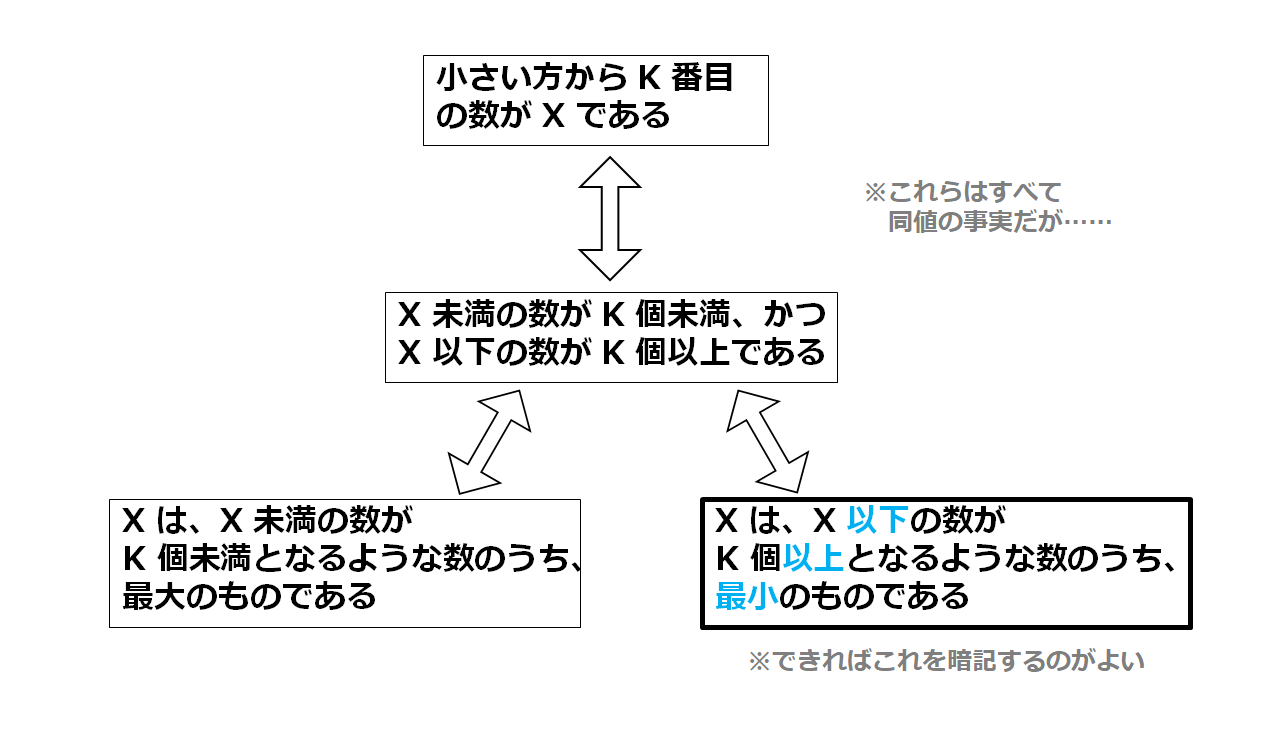
　「小さい方から $K$ 番目の数が $X$」
⇔「$X-1$ 以下の数は $K$ 個未満で、$X$ 以下の数は $K$ 個以上」
⇔「$X$ 以下の数が $K$ 個以上となる最小の $X$」

　考え方としては、

• $X-1$ 以下の数（＝$X$ 未満の数）が $K$ 個以上ある場合は確実にアウト
• 一方、$X$ 以下の数が $K$ 個以上あってもセーフ

　という感じかと思います。個人的には、こういう一見して自明でない公式は 暗記した方がいい（なぜなら、手で覚えるぐらいのレベルでないと、本番では安定して使えないため）と考えているので、細かいことは気にせず、

• 小さい方から $K$ 番目の数は、$X$ 以下の数が $K$ 個以上となる最小の $X$

　と覚えることをおすすめします。

　検証用に、決め打ち二分探索を使う系の代表的問題であると思われる ARC037-C のコードを載せます。

// 筆者の提出（https://atcoder.jp/contests/arc037/submissions/67265219）をAIで改造
#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, k;
    std::cin >> n >> k;

    std::vector<int> a(n), b(n);
    for (int i = 0; i < n; ++i) {
        std::cin >> a[i];
    }
    for (int i = 0; i < n; ++i) {
        std::cin >> b[i];
    }

    // b をソートしておく
    std::sort(b.begin(), b.end());

    // 二分探索の初期値
    long long ng = 0;            // この値では k 個以上 <= とはならない
    long long ok = 1000000000000000000LL; // この値では k 個以上 <= となる

    while (ok - ng > 1) {
        long long mid = (ng + ok) / 2;
        long long cnt = 0;

        // 各 a[i] について mid / a[i] 以下の b[j] の数を数える
        for (int i = 0; i < n; ++i) {
            long long limit = mid / a[i];
            cnt += std::upper_bound(b.begin(), b.end(), limit) - b.begin();
        }

        if (cnt >= k) {
            ok = mid;
        } else {
            ng = mid;
        }
    }

    std::cout << ok << "\n";
    return 0;
}

　ちなみに、ある配列（ソート済）の中で $X$ 以下の個数を求める場合は、upper_bound で求めたインデックスがそのまま答えとなります。これも過去記事で理論的背景を解説していますが、細かい理屈を考えずに覚えた方がいい です。

　更に言うと、「配列 $A$ の要素をすべて $R$ 倍したものにおいて、$X$ 以下となる要素の個数」と、「配列 $A$ において、$\lfloor \frac{X}{R} \rfloor$ 以下となる要素の個数」は厳密に一致しますが、これも覚えた方が（以下略

「超過または以下」を求める場合は切り下げ除算で大丈夫ですが、「以上または未満」を求めるとき（lower_bound はこれにあたります）は切り上げにしないといけないので注意してください。理論的背景は、直前に挙げた過去記事で説明しています。

ほかの言い換え

　条件を整理すると以下のようになります。

　左の「未満」から攻める方法でも書いてみます。

#include <iostream>
#include <vector>
#include <algorithm>

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, k;
    std::cin >> n >> k;

    std::vector<int> a(n), b(n);
    for (int i = 0; i < n; ++i) {
        std::cin >> a[i];
    }
    for (int i = 0; i < n; ++i) {
        std::cin >> b[i];
    }

    // b をソートしておく
    std::sort(b.begin(), b.end());

    // ── 初期化を反転 ──
    long long ok = 0;                              // ← 以前の ng 相当の初期値
    long long ng = 1000000000000000000LL;          // ← 以前の ok 相当の初期値

    while (ng - ok > 1) {
        long long mid = (ng + ok) / 2;
        long long cnt = 0;

        // 各 a[i] について mid / a[i] 以下の b[j] の数を数える
        for (int i = 0; i < n; ++i) {
            long long limit = mid / a[i];
            // ── upper_bound → lower_bound に変更 ──
            cnt += std::lower_bound(b.begin(), b.end(), limit) - b.begin();
        }

        // ── 比較演算子を反転 ──
        if (cnt < k) {
            ok = mid;
        } else {
            ng = mid;
        }
    }

    std::cout << ok << "\n";
    return 0;
}

　実はこれ、バグが出ます。

            long long limit = mid / a[i];

　ここが問題で、lower_bound で使うためには繰り上げにする必要があります。なので、正しくは、

            long long limit = (mid+a[i]-1) / a[i];

　となります。本番でこんなバグを踏んだら泣きたくなります。

　このようなことから、筆者としては図の右の方法（＝「以下」から攻める方法）を推奨します。理由は以下の通りです。

• 「以下」を求める限りにおいては、整数除算で余計な対策をしなくてよい
• 「最大値を最小化する」というスタンダードな二分探索の考え方と一致する

「大きい方から」の場合

　「大きい方から」の場合も、同様に考えていきます。

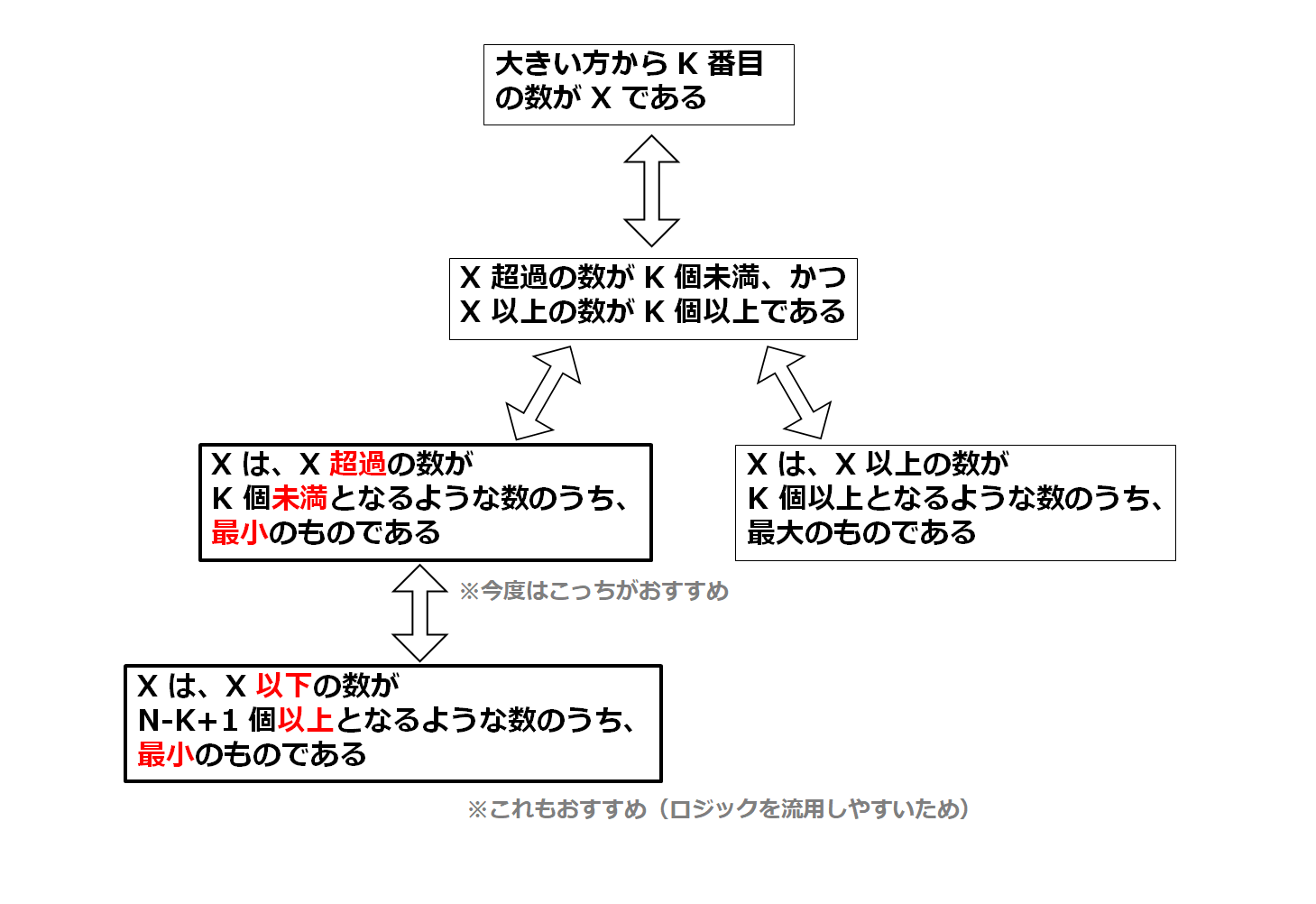
• $X$ 超過の数が $K$ 個未満となるような最小の $X$
• $X$ 以上の数が $K$ 個以上となるような最大の $X$

　どちらがバグを生みづらいかわかるでしょうか。「超過」を使い、かつ「最小化」を行う前者です。

　または、

• $X$ 以下の数が $N-K+1$ 個以上となるような最小の $X$

　という言い換えもおすすめです。本質的にはあまり変わりませんが、「小さい方から」を求めるやり方をほとんど流用できるからです。

結論

　という訳で、冒頭の結論に至ります。

　長さ $N$ の配列において、

• $K$ 番目に小さい数は、「$X$ 以下となるような数が $K$ 個以上となるような最小の $X$ 」
• $K$ 番目に大きい数は、「$X$ 超過となるような数が $K$ 個未満となるような最小の $X$」
  • または、「$X$ 以下となるような数が $N-K+1$ 個以上となるような最小の $X$」