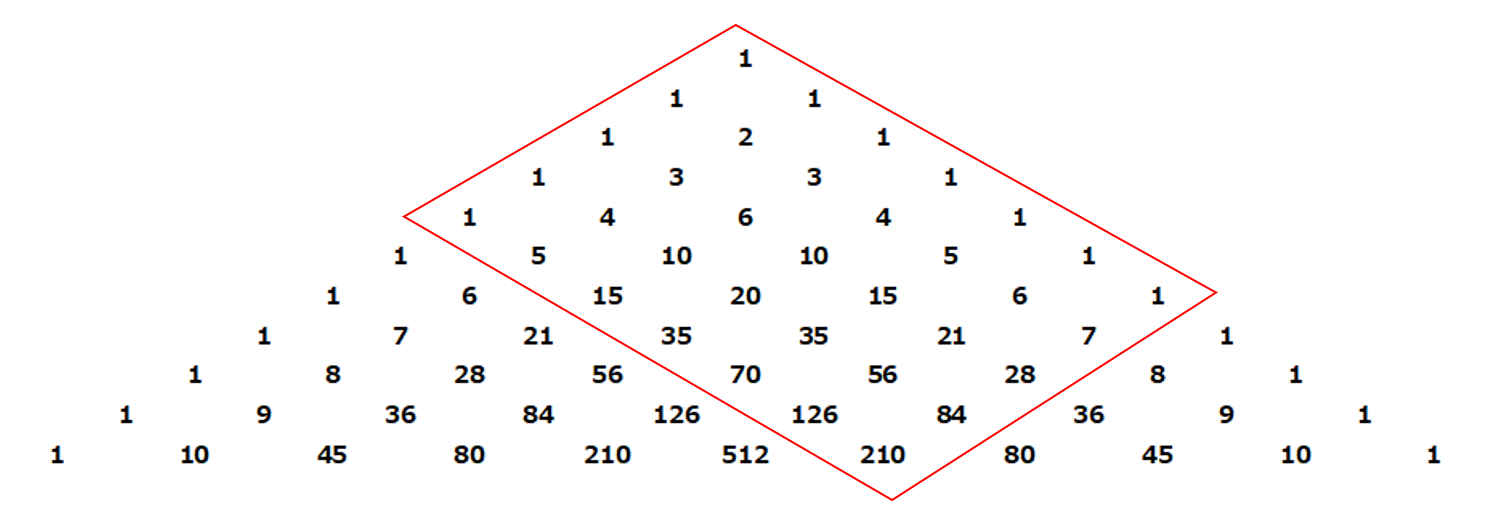
いわゆる二項係数${}_nC_r$がパスカルの三角形により計算できることは、わりと知られた事実だと思います。
上段の2つの数字を足したら下段の数が計算できます。
これは数式の変換によって確認することもできますが、もう少し幾何的な見方をしてみます。
最短経路問題
${}_nC_r$は最短経路問題であると見ることもできます。
上のようなグリッドで、右下の至るまでの道筋は何通りありますか、という問題に置き換えることができます。(上の図では$n=10,r=4$)
これを最短経路問題的に考えたら、単純な動的計画法の問題に帰着できます。動的計画法というと大仰に聞こえますが、要は以下の遷移(漸化式といってもいいでしょう)を繰り返すということです。
「自分のマスに至る道筋の数は、上のマスへの道筋の数と、左のマスへの道筋の数を合計したものである。」
プログラム的に書くと、
dp[i+1][j] += dp[i][j];
dp[i+1][j+1] += dp[i][j];
です。
グリッド上を下か右にしか行けないのであれば、上の推論はほぼ自明となります。これはパスカルの三角形で行っている計算と同一になります。上の表はパスカルの三角形の一部を切り出したものになることが確認できます。
組み合わせ問題
と同時に、これは組み合わせ問題になります。下に4マス、右に6マス移動したい時、最終的な数が合っていれば、どのタイミングで下もしくは右に行くのは自由ですので、求める答えは
下下下下右右右右右右
下下下右下右右右右右
下下下右右下右右右右
.
.
.
といろいろな組み合わせを考えることができます。これは順番を考えない並べ替えですので、 $ _{10} C _4$で求めることができます。
_{10} C _4 = \frac{10 \cdot 9 \cdot 8 \cdot 7}{1 \cdot 2 \cdot 3 \cdot 4} = 210
二項係数の合計
二項係数の合計が$2^n$になることも、組み合わせとして考えることができます。
二項係数の合計は、グリッドでいうと斜めのラインの合計になります。これは下と右の合計が一緒ということなので。$n=$3の時
下下下
下下右
下右下
下右右
右下下
右下右
右右下
右右右
となります。要は、「下か右」という2つの選択を3回行っています。ことのことから、$n$の二項係数の合計が$2^n$になることがわかります。
フィボナッチ数列
パスカルの三角形を以下のように少し変形します。
この時、斜めの合計($1,1,2,3,5,...)$はフィボナッチ数列に一致します。
これも幾何的に見ればほぼ自明で、
1個前の列からは下の矢印で、2個前の列からは斜めの矢印ですべての値を受け取っているので、$a_{n+2}=a_{n+1}+a_n$すなわちフィボナッチ数列の関係性が成り立っていることがわかります。
一般化
多変数への一般化を考えてみます。
二項係数
二項係数は多項係数へと拡張できますが、組み合わせで考えるとわかりやすいです。
例えば赤2個、緑3個、青4個を並べ替える場合、
- 9個全てを区別して並べる
- 赤同士の区別をなくす
- 緑同士の区別をなくす
- 青同士の区別をなくす
と考えた場合、それぞれの組み合わせは$9!,2!,3!,4!$となり、答えは
\frac{9!}{2!3!4!}=1260
となります。要は下の階乗を増やしていくだけで多変数に拡張できます。
よって多項係数の一般項は
\frac{n!}{k_1!k_2!\cdots k_r!}
となります。
三角形
パスカルの三角形は、3次元まではイメージしやすい形で拡張できます。名付けるなら、パスカルの三角錐でしょうか。
最短経路問題のDPも、例えば3次元では、
dp[i+1][j][k] += dp[i][j][k]
dp[i+1][j+1][k] += dp[i][j][k]
dp[i+1][j+1][k+1] += dp[i][j][k]
となりますが、多変数でも変数を増えすだけで自然に拡張できます。理論的にはパスカルの超立体を考えればいくらでも幾何的アナロジーを考えることができますが、人間の感覚を少々超越しています。
フィボナッチ
パスカルの三角錐を斜めに横断したものの合計はトリボナッチ数列になります。さすがに図示できないので計算結果だけ。
1 = 1
1 = 1
1+1 = 2
1+2+1 = 4
2+1+3+1 = 7
2+3+3+4+1 = 13
1+6+1+4+6+5+1 = 24
3+3+12+4+5+10+6+1 = 44
3+6+12+1+20+10+6+15+7+1 = 81
1+12+4+10+30+5+30+20+7+21+8+1 = 149
なお、トリボナッチ数列の一般項はとても煩雑であることが知られています。
競プロで使う場合
上記の表を埋めることによって、競技プログラミングにおいても二項係数を高速で求めることができます。
しかしパスカルの三角形を埋めるにはn^2のテーブルが必要です。10^9を超えたあたりで(少なくともAtCoderでは)メモリオーバーするので、対応できるnは現実的には10^4まででしょうか。それよりも大きい数に対応するには階乗の除算で算出する方法に切り替える必要があります。そういう場合はだいたい逆元も求める必要があるので、実装がとてもめんどくさいことになりますが、それはまたの機会に。
中央二項係数
二項係数のピーク、即ち中央二項係数は、以下の式で近似できます。
{}_{2n} C_n \simeq \ \frac{4^n}{\sqrt{\pi n}}
二項分布${}_n C_r$の合計は$2^n$なので、二項分布の各項を$2^n$で割ったものは、それらの合計が$1$となる確率分布となります。またその確率分布は、中心極限定理により平均$np$、分散$np(1-p)$の正規分布に近づきます。
この性質を利用して上の等式を証明することができます。
${}_{2n} C_n, p=\frac{1}{2}$の時、分散は$2n\frac{1}{2}(1-\frac{1}{2}) = \frac{n}{2}$となります。
\frac{{}_{2n} C_n}{2^{2n}} = \frac{1}{\sqrt{2\pi \frac{n}{2}}}e^0 \\
\frac{{}_{2n} C_n}{4^n} = \frac{1}{\sqrt{\pi n}} \\
\Leftrightarrow {}_{2n} C_n = \frac{4^n}{\sqrt{\pi n}} \\
※nが十分に大きい時