二次システムのステップ入力時間応答

概要

タイトル通りです．
ステップ応答を初期値込みで検証します．
ただし，導出はしません．
最後はScilabで検証します．
参考サイト：
https://tajimarobotics.com/second-order-system-step-response/
http://ysserve.wakasato.jp/Lecture/ControlMecha1/node15.html
http://www.fl.ctrl.titech.ac.jp/text_old/Feedback/materials/chap3.pdf

二次システム

G(s) = A \frac{w_n^2}{s^2 +2 \zeta wn s+w_n^2} 

が二次システムです．$A$は振幅で一般的なゲインです．
ステップ入力した場合，最終的に$A$に収束します．

\frac{Y(s)}{U(s)} = A \frac{w_n^2}{s^2 +2 \zeta w_n s+w_n^2} \\
\therefore (s^2 +2 \zeta w_n s+w_n^2)Y(s) = A w_n^2 U(s)\\
\therefore y''(t) +2 \zeta w_n y(t)'+w_n^2y(t) = A w_n^2 u(t)\\

を必ず満たす．

ステップ応答:過減衰の場合

まず，過減衰の場合のステップ応答は

y(t)=A \{ 1-\frac{e^{- \zeta w_n t}}{\sqrt{\zeta^2-1}} sinh(\sqrt{\zeta^2-1} w_n t + tanh^{-1} \frac{\sqrt{\zeta^2-1}}{\zeta} )\}

らしい．$tan$ではなく，$tanh$であることに注意

y''(t) +2 \zeta w_n y(t)'+w_n^2y(t) = A w_n^2 *1\\

を満たすか確かめる．
ハイパボリックサイン・コサインがあるが基本的に演算はsin/cosと同じ.
ただし

(sinh(x))' = cosh(x)\\
(cosh(x))' = sinh(x)\\

となり，coshの微分は符号反転は入らない！

a = \frac{1}{\sqrt{\zeta^2-1} }\\
b=tanh^{-1} \frac{\sqrt{\zeta^2-1}}{\zeta}\\
y(t) =A-Aae^{- \zeta w_n t}sinh(\sqrt{\zeta^2-1} w_n t +b)

とする.

y'(t) = Aae^{- \zeta w_n t} \{ \zeta w_n sinh(\sqrt{\zeta^2-1} w_n t +b) -  \sqrt{\zeta^2-1}w_n cosh(\sqrt{\zeta^2-1} w_n t +b)\}\\
y''(t) = A ae^{- \zeta w_n t} \{- \zeta^2 w_n^2 sinh(\sqrt{\zeta^2-1} w_n t +b) +  \zeta \sqrt{\zeta^2-1}w_n^2 cosh(\sqrt{\zeta^2-1} w_n t +b)\\
+\zeta\sqrt{\zeta^2-1}  w_n^2 cosh(\sqrt{\zeta^2-1} w_n t +b) -  (\zeta^2-1)w_n^2 sinh(\sqrt{\zeta^2-1} w_n t +b)

\}\\

代入し

y''(t) +2 \zeta w_n y(t)'+w_n^2y(t)\\
=A ae^{- \zeta w_n t} \{
sin(\sqrt{\zeta^2-1} w_n t +b) (- \zeta^2 w_n^2 -  (\zeta^2-1)w_n^2 + 2\zeta^2 w_n^2 -w_n^2)\\
+cos(\sqrt{\zeta^2-1} w_n t +b)(+  \zeta \sqrt{\zeta^2-1}w_n^2 +\zeta\sqrt{\zeta^2-1}  w_n^2-  2\sqrt{\zeta^2-1}w_n^2 \zeta ) 

\}\\
+Aw_n^2\\
=Aw_n^2

よって

y''(t) +2 \zeta w_n y(t)'+w_n^2y(t) = A w_n^2 *1\\

を満たすことを確かめられた．
$a,b$についてはなんでもいいというのは式の流れからわかる．
初期値が変わった場合，$a,b$を調整すればよいということになる．

ステップ応答:過減衰：初期値が0でない場合

y(t)=A \{ 1-a e^{- \zeta w_n t}  sinh(\sqrt{\zeta^2-1} w_n t + b )\}

は$t=0$の時

y(0) = A(1-a \cdot sinh(b))\\

で，

y'(t) = Aae^{- \zeta w_n t} \{ \zeta w_n sinh(\sqrt{\zeta^2-1} w_n t +b) -  \sqrt{\zeta^2-1}w_n cosh(\sqrt{\zeta^2-1} w_n t +b)\}\\
y'(0) = Aa\{ \zeta w_n sinh( +b) -  \sqrt{\zeta^2-1}w_n cosh( +b)\}\\

加法定理を使うために

\gamma cosh(\beta) = \zeta w_n\\
\gamma sinh(\beta) = -  \sqrt{\zeta^2-1}w_n\\

となる，$\zeta,\gamma$を求める

\gamma^2 = \gamma^2(cosh^2(\beta) -sinh^2(\beta)) = (\zeta w_n)^2 - (-  \sqrt{\zeta^2-1}w_n)^2 = w_n^2 \\
\therefore  \gamma = w_n

よって

cosh(\beta) = \zeta\\
sinh(\beta) =  -  \sqrt{\zeta^2-1}\\

よって，

\beta= -tanh^{-1}  \frac{\sqrt{\zeta^2 -1}}{\zeta}

とすれば，

y'(0) = Aa\ w_n sinh( b -tanh^{-1}  \frac{\sqrt{\zeta^2 -1}}{\zeta}) \\

となる

以上の二つの式

y(0) = A(1-a \cdot sinh(b))\\
y'(0) = Aa\ w_n sinh( b -tanh^{-1}  \frac{\sqrt{\zeta^2 -1}}{\zeta}) \\

を連立して，$a,b$を決定することで，yの初期値に合わせた解が得られる．

ステップ応答:過減衰：初期値が0のとき

$y'(0)=0$より

sinh(b-tanh^{-1} \frac{\sqrt{\zeta^2 -1}}{\zeta} )  = 0\\
\therefore b = tanh^{-1} \frac{\sqrt{\zeta^2 -1}}{\zeta}\\

$y(0)=0$より

1= a \cdot sinh(b)\\
\therefore a = 1/sinh(tanh^{-1} \frac{\sqrt{\zeta^2 -1}}{\zeta})\\

ここが，普通の三角関数と違うため，だいぶ引っ掛かりましたが

tanh(\phi)=b/a

の時

sinh(\phi) = \frac{b}{\sqrt{a^2+b^2}}

とはなりません．三角関数ではなりますが．では$b/a$が与えられたとき$sinh(\phi)$はどうなるでしょうか．

1-tanh^2 = \frac{1}{cosh^2}\\
\therefore cosh^2 = \frac{1}{1-tanh^2} = \frac{a^2}{a^2-b^2}\\
\therefore 1+sinh^2 = \frac{1}{1-tanh^2} \\
\therefore sinh^2 = \frac{1}{1-tanh^2} -1 = \frac{b^2}{a^2-b^2}\\

よって，ルートを取る際はwikiのグラフを見ると納得できます．

sinh(\phi) = \frac{b}{\sqrt{a^2-b^2}}

になります．ルート内の符号が変わりました．

よって，

1= a \cdot sinh(b)\\
\therefore a = 1/sinh(tanh^{-1} \frac{\sqrt{\zeta^2 -1}}{\zeta})\\
\therefore a = \frac{1}{\sqrt{\frac{\zeta^2-1}{\zeta^2 -(\zeta^2-1)} }}\\
 =\frac{1}{\sqrt{\zeta^2-1}}

y(t)=A \{ 1-\frac{1}{\sqrt{\zeta^2 -1}}  e^{- \zeta w_n t}  sinh(\sqrt{\zeta^2-1} w_n t + tanh^{-1} \frac{\sqrt{\zeta^2 -1}}{\zeta} )\}

ステップ応答:減衰振動の場合

y(t) = A\{1- a e^{- \zeta w_n t}  sin(\sqrt{1-\zeta^2} w_n t + b )\}

として，検証する

y'(t) = Aae^{- \zeta w_n t} \{\zeta w_n sin(\sqrt{1-\zeta^2} w_n t + b ) - \sqrt{1-\zeta^2} w_n cos(\sqrt{1-\zeta^2} w_n t + b )\} \\


y''(t) = Aae^{- \zeta w_n t} \{-\zeta^2 w_n^2 sin(\sqrt{1-\zeta^2} w_n t + b ) + \sqrt{1-\zeta^2} \zeta w_n^2 cos(\sqrt{1-\zeta^2} w_n t + b )\\
+\zeta w_n \sqrt{1-\zeta^2} w_n cos(\sqrt{1-\zeta^2} w_n t + b ) + \sqrt{1-\zeta^2} w_n \sqrt{1-\zeta^2} w_nsin(\sqrt{1-\zeta^2} w_n t + b )\} \\

よって

y''(t) +2 \zeta w_n y(t)'+w_n^2y(t)\\
=A ae^{- \zeta w_n t} \{
sin(\sqrt{1-\zeta^2} w_n t + b )  (-\zeta^2 w_n^2+ \sqrt{1-\zeta^2} w_n \sqrt{1-\zeta^2} w_n+2\zeta^2 w_n^2 -w_n^2)\\
+cos(\sqrt{1-\zeta^2} w_n t + b ) (+ \sqrt{1-\zeta^2} \zeta w_n^2+\zeta w_n \sqrt{1-\zeta^2} w_n - 2\sqrt{1-\zeta^2} \zeta w_n^2)
\}\\
+A w_n^2\\
=A w_n^2\\

よって，微分方程式を満たすことを確認できた．

ステップ応答:減衰振動:初期値0の時

y(t) = A\{1- a e^{- \zeta w_n t}  sin(\sqrt{1-\zeta^2} w_n t + b )\}

より

y(0) =A(1-asin(b))\\
y'(0) = Aaw_nsin(b-tan^{-1} \frac{\sqrt{1-\zeta^2 }}{\zeta})\\

よって

b=tan^{-1} \frac{\sqrt{1-\zeta^2}}{\zeta}\\
a=1/sin(b)\\
=\frac{1}{\sqrt{1-\zeta^2}}

よって

y(t) = A\{1- \frac{1}{\sqrt{1-\zeta^2}} e^{- \zeta w_n t}  sin(\sqrt{1-\zeta^2} w_n t + tan^{-1} \frac{\sqrt{1-\zeta^2}}{\zeta} )\}

となる．

Scilabで検証

過減衰

w_n = 1\\
\zeta = 1.2\\
A=1\\

として，ステップ応答を2通りで計算する

y(t)=A \{ 1-\frac{1}{\sqrt{\zeta^2 -1}}  e^{- \zeta w_n t}  sinh(\sqrt{\zeta^2-1} w_n t + tanh^{-1} \frac{\sqrt{\zeta^2 -1}}{\zeta} )\}

1. scilabのcsimを使用

y''(t) +2 \zeta w_n y(t)'+w_n^2y(t) = A w_n^2 u(t)\\

を状態方程式に直すと

\dot{x} = 
 \left(
    \begin{array}{ccc}
      -2\zeta w_n &-w_n^2\\
1&0\\
    \end{array}
  \right)
x +
 \left(
    \begin{array}{ccc}
   Aw_n^2\\
0\\
    \end{array}
  \right)
u(t)\\
y= \left(
    \begin{array}{ccc}
     0&1\\
    \end{array}
  \right)

である．

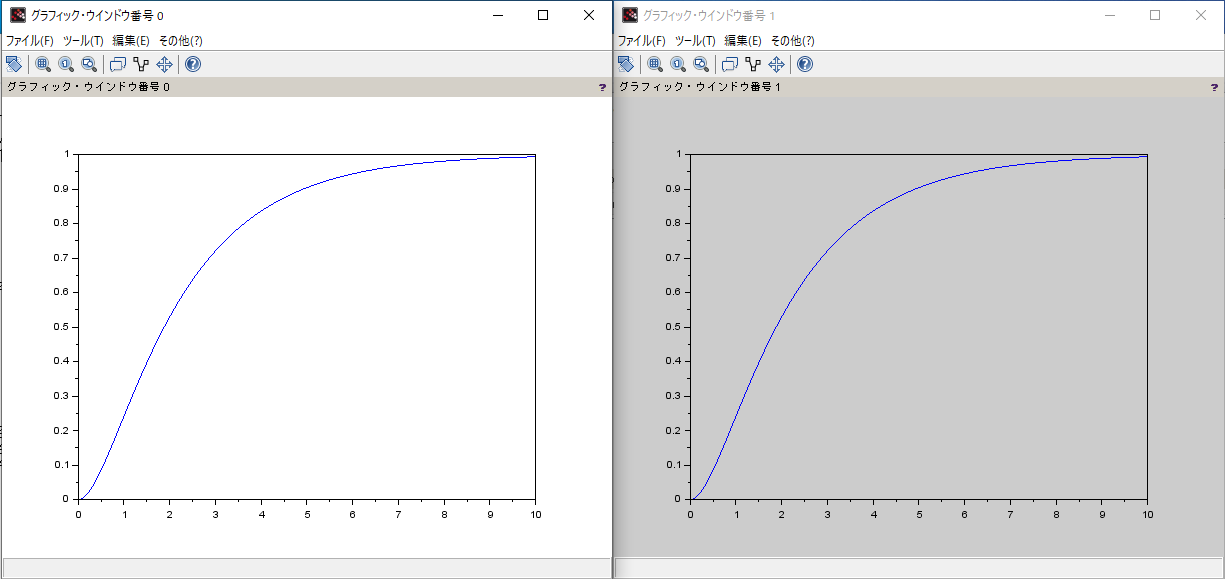
結果

ちゃんと同じになった

プログラム

clear();
for i = 1:10 do
    close
end

zeta = 1.2
wn = 1
a = 1

A=[-2*zeta*wn -1*wn^2
1 0]

B=[a*wn^2
0]

C=[0 1]
D=[0]

x0=[0
0]

sl = syslin('c',A,B,C,D,x0);


t=0:0.01:10;
y=csim('step',t,sl)

y2= diag(a*(1- 1/sqrt(zeta^2-1) *exp(-zeta*wn*t')*sinh(sqrt(zeta^2-1)*wn*t+atanh(sqrt(zeta^2-1)/zeta) ) ))
clf();
plot(t,y);
figure();
plot(t,y2);

出力が，y'の時

過減衰

y(t) =A \{ 1-ae^{- \zeta w_n t}sinh(\sqrt{\zeta^2-1} w_n t +b) \}\\
y'(t) = Aae^{- \zeta w_n t}\{ \zeta w_n sinh(\sqrt{\zeta^2-1} w_n t +b)  - \sqrt{\zeta^2-1} w_n cosh(\sqrt{\zeta^2-1} w_n t +b) \}\\
=Aae^{- \zeta w_n t} w_n sinh(\sqrt{\zeta^2-1} w_n t +b -tanh^{-1} \frac{\sqrt{\zeta^2 -1}}{\zeta} ) 

ただし，$a,b$は次の初期値で決定する

y(0) = A(1-a \cdot sinh(b))\\
y'(0) = Aa\ w_n sinh( b -tanh^{-1}  \frac{\sqrt{\zeta^2 -1}}{\zeta}) \\

初期値がすべて0の時

y'(t) = A \frac{1}{\zeta^2-1}e^{- \zeta w_n t} w_n sinh(\sqrt{\zeta^2-1} w_n t ) 

位相項が0になります．

減衰振動

y(t) = A\{1- a e^{- \zeta w_n t}  sin(\sqrt{1-\zeta^2} w_n t + b )\}\\
y'(t) = Aae^{- \zeta w_n t} w_n sin(\sqrt{\zeta^2-1} w_n t +b -tan^{-1} \frac{\sqrt{1-\zeta^2}}{\zeta} ) 

ただし，$a,b$は次の初期値で決定する

y(0) =A(1-asin(b))\\
y'(0) = Aaw_nsin(b-tan^{-1} \frac{\sqrt{1-\zeta^2 }}{\zeta})\\

初期値がすべて0の時

y'(t) = A \frac{1}{1-\zeta^2}e^{- \zeta w_n t} w_n sin(\sqrt{1-\zeta^2} w_n t ) 

同様に，位相項が0になります．

感想

双曲線関数を三角関数と同じとみなして，計算処理は絶対にしてはいけない！！！
どう頑張っても合わないと，すごい悩んでしまったが，すべてハイパボリックの計算を勘違いしていたためだった．