ソフトウェアテスト技法

はじめに

テストについて学び中なので、いくつかのテスト技法を簡単にまとめ

テスト技法の目的

まず前提として、テスト技法全般における目的は、「より少ないテストケースで、高い網羅性を確保すること」

同値クラスと境界値テスト

同値クラス

テスト的には同じ意味になる値のこと

例）以下のコードなら、a=1 も a=2 も同じ処理ブロックに入るので、同値クラスと言える

if a < 5:
  # 
else a < 10:
  #
else:
  #

境界値テスト

• 同値クラスの境界と、その前後を調べるテスト
• 例）上の例では、a=5、a=10 が境界値となるので、それぞれの前後の値である a=4, 5, 6、a=9,10,11 をテストする

ドメイン分析テスト

複数の条件による論理のテストケースで、抜け漏れを防ぐための技法で、条件同士が相互作用を持つ場合に有効なテスト技法

4つのポイント

ポイント名	説明	x >= 10 の場合	x > 10 の場合
on	境界上の値	10	10
off	境界に隣接する値	9	11
in	on/off 以外のドメイン内の値	15 など	15 など
out	on/off 以外のドメイン外の値	5 など	5 など

ドメインマトリクス

例）下記のコードをテストする場合

if a >= 5 and a + b >= 10:
  # A
else:
  # B

ドメインマトリクスは以下のようになる

変数	条件	ポイント	1	2	3	4
a	a >= 5	on	5
		off		4
		in			6	7
a + b	a+b >= 10	on			6 + 4
		off				7+2
		in	5 + 6	4 + 7
結果			A	B	A	B

• ケース 1, 2 は、a+b を in に固定して、 a が on と off を取るようなケース
• ケース 3, 4 は、a を in に固定して、 a+b が on と off を取るようなケース

この 4 つのケースで網羅性を確保する

デシジョンテーブル

複数の条件による論理のテストケースで、抜け漏れを防ぐための技法で、条件同士が独立していて、込み入った論理関係を持つ場合に有効なテスト

例）条件 x, y, z がすべて真だったら処理A、それ以外なら処理B のような場合、デシジョンテーブルは以下のようになる（ T = true、F = false）

条件	1	2	3	4	5	6	7	8
x	T	T	T	T	F	F	F	F
y	T	T	F	F	T	T	F	F
z	T	F	T	F	T	F	T	F
結果	A	B	B	B	B	B	B	B

8 個のテストケースで網羅できる

デシジョンテーブルの圧縮

条件判定に順番がある場合、網羅性を保ちつつテストケースを減らすことができる

例えば、上記の例が x → y → z の順で判定されることが分かっている場合（以下のようなロジックの場合）

if x:
  if y:
    if z:
      # 処理A
    else:
      # 処理B
  else:
    # 処理B
else:
  # 処理B

この場合、4 つのテストケースで網羅することができる

条件	1	2	3	4
x	T	T	T	F
y	T	T	F	-
z	T	F	-	-
結果	A	B	B	B

ペア構成テスト

複数の条件を持つ複雑な組み合わせをテストする場合、すべてを網羅するのが難しいので、少ないテストケースである程度の網羅性を確保することを目指す

　× すべての条件の組み合わせでテスト
　〇 すべてのペアの組み合わせでテスト

ほとんどのバグ（70～85 %程度）は、シングルモード欠陥、ダブルモード欠陥のいずれかなので、ペアの組み合わせをテストすれば、高い網羅性を確保できる

例）3つの条件 x, y, z が、2値の値を持つ場合

「x と y」「x と z」「y と z」の3通りの組み合わせそれぞれに対して、「0, 0」「0, 1」「1, 0」「1, 1」の 4通りの値に対してテストする（＝12 通り）

直行表

直行表とは、すべてのペアを抜けもれなく網羅する方法

上の例の直行表は以下のようになる

	x	y	z
1	0	0	0
2	0	1	1
3	1	0	1
4	1	1	0

上記の 4つのテストケースで、「x と y」「x と z」「y と z」の組み合わせそれぞれに対して、「0, 0」「0, 1」「1, 0」「1, 1」の 4通りの組み合わせを試すことができる

4つの条件 a, b, c, d が、3値の値「0, 1, 2」を持つ場合の直行表は以下のようになる

a	a	b	c	d
1	0	0	0	0
2	0	1	1	1
3	0	2	2	2
4	1	0	1	2
5	1	1	2	0
6	1	2	0	1
7	2	0	2	1
8	2	1	0	2
9	2	2	1	0

上記の 9つのテストケースで、すべてのペアの組み合わせに対してテストできる

すべての条件を網羅すると 81通り必要になるため、大幅にテストケースを削減することができる

直行表の表記法

• 2 値 3 条件 の直行表　→　L4(2^3) と表記する（4 行、2 値、3 条件の意）
• 3 値 4 条件の直行表　→　L9(3^4)
• 2 値が4条件、4値が1条件の直行表　→　L8(2^4 4^1)

直行表はさまざまなサイトで公開されているので、自身で直行表を作成しなくても、この表記をもとに使いたものを探せばOK

直行表を使ったテストケース作成の手順

1. 条件をすべて洗い出す
2. 各条件が取り得る値の数を決める
3. 1. 1. の条件に合う直行表を選択する（完全一致するものがない場合は、大きめの直行表を選ぶ）
4. 直行表にテスト対象の条件を当てはめる

状態遷移テスト

現在の状態と、その遷移によって振る舞いが変わるソフトウェアをテストする手法

状態遷移図

「状態」「遷移」「イベント」の 3 つからなる

• 遷移は状態間を繋ぐ矢印
• イベントは遷移を発生させるもの
• 初期状態は黒丸（●）、終了状態は二重黒丸（◉）で表現する

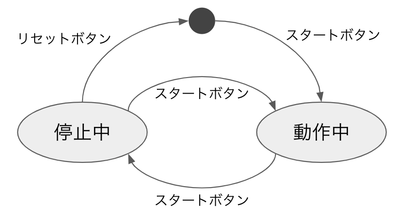
例）ストップウォッチの状態遷移図

• 初期状態でボタンを押すと動作する
• 動作中にボタンを押すと停止する
• 停止しているときにボタンを押すと再び動作する
• 停止しているときにリセットボタンを押すと初期状態になる

これを状態遷移図にすると下記のようになる

状態遷移図からテストケースを作成する。この場合、少なくともすべての遷移がテストされている必要があるので、以下のようなテストケースが考えられる

• 「初期状態」でスタートボタンを押すと「動作中」になること
• 「動作中」でスタートボタンを押すと「停止中」になること
• 「停止中」でスタートボタンを押すと「動作中」になること
• 「停止中」でリセットボタンを押すと「初期状態」になること

上記のテストケースを実施しても、すべての条件を網羅できてはいない

より網羅的なテストケースを考えるには、状態遷移表が使える

状態遷移表

イベント \ 状態	初期状態	動作状態	停止状態
スタートボタン	動作状態	停止状態	動作状態
リセットボタン	N/A	N/A	初期状態

状態遷移表を書くことで抜け漏れを確認することができ、6 つの遷移を網羅することができる

このように、6 つの遷移をテストすれば状態の1段階の遷移は確認できるが、「停止中」→「動作状態」→「停止状態」のような 2段階以上の遷移をテストすることができない

これを考えるために、Ｎスイッチカバレッジがある

Nスイッチカバレッジ

遷移前/後の状態を行/列にして、関係行列を作成する

前状態 \ 後状態	初期状態	動作状態	停止状態
初期状態	リセットボタン	スタートボタン
動作状態	リセットボタン		スタートボタン
停止状態	リセットボタン	スタートボタン

関係行列を行列式とみなして、二乗すると以下のようになる（S=スタートボタン、R＝リセットボタン）

前状態 \ 後状態	初期状態	動作状態	停止状態
初期状態	RR+SR	RS	SS
動作状態	RR+SR	RS+SS
停止状態	RR+SR	RS	SS

このテストケースは「停止中」→「動作状態」→「停止状態」のような 2段階の遷移を網羅している。

前状態から後状態の途中の状態（例えば、「停止中」→「動作状態」→「停止状態」という遷移なら途中の「動作状態」）を「スイッチ」と呼ぶ。このケースはスイッチ（途中の状態）が 1つなので 1スイッチカバレッジと呼ぶ。

さらに 2スイッチカバレッジを作るには、最初の関係行列を 3乗することで得られる。