初めに
この記事は準同型暗号の最前線1(入門編)の続きです。
私たちが提案したL2準同型暗号の原理を解説します。
金庫開けクイズ
まず簡単なクイズから始めましょう。
ここに金庫があり、その金庫には24個の歯があるダイヤルがついています。
ダイヤルには赤の矢印がついています。ダイヤルを回して赤の矢印が青の矢印の先に来たら金庫が開くとします。ただしダイヤルは歯車5個分づつしか動かせません。ダイヤルを何回時計回りに動かせば金庫は開くでしょうか。
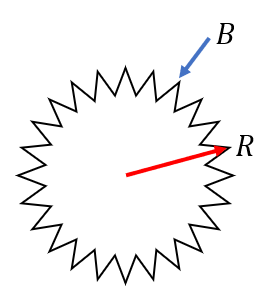
実際に数えながらやってみると9回動かすと赤の矢印($R$)が青の矢印($B$)ところに来ました。このことを$9R = B$と書くことにしましょう。
離散対数問題
今の金庫開けクイズは容易でしたが、歯車の数が多くなると大変そうです。
一般に赤と青の矢印$R$, $B$が与えられたときに
$? R = B$
となる$?$を求めなさいという問題を離散対数問題といいます。
歯車を「楕円曲線」の中に作ると離散対数問題がとても難しくなるということが経験的に知られています。この性質を使って作られた暗号を「楕円曲線暗号」といいます。
ちなみに「楕円曲線」は「楕円」と「曲線」がくっついた用語ですが、「楕円」でも「曲線」でもありません。このあたりの話は暗号文のままで計算しよう - 準同型暗号入門をごらんください。
楕円曲線暗号
歯車の一つ分を$P$とします。秘密の数字を適当に選んで$s$とします。ダイヤルの真上から時計回りに$s$番目の歯車を$Q = sP$とします。
$s$が秘密鍵で$Q$が公開鍵です。
金庫開けクイズの歯車では$Q$が分かれば角度から$s$が求まりますが、楕円曲線の中の歯車はそんなことができないので秘密鍵は分かりません。
暗号文は次のように作ります。
歯車のどれか一つを選び$M$とします。そこから適当な乱数$r$を決めて$Q$ずつ$r$回回します。その場所は
$M + rQ$
と表せます。この場所と場所$rP$のペア
$(M + rQ, rP)$
をMの暗号文$Enc(M)$とします。$Enc(M) = (M + rQ, rP)$.
秘密鍵$s$を持っている人は次のようにして復号できます。
$rP$という場所を一目盛りとして$s$回回します。
するとその場所は$s(rP)$になりますが、
$s(rP) = r(sP) = rQ$
という関係がなりたちます。$Enc(M)$の一つ目の要素$M + rQ$から$rQ$を引いて$M$を得ます。
まとめて書くと暗号文が$(S, T)$の形のときに
$Dec((S, T)) = S - sT$
であり、
$Dec(Enc(M)) = Dec((M + rQ, rP)) = (M + rQ) - s(rP) = M$
です。この暗号方式を楕円ElGamal暗号といいます。
加法性
前節で紹介した楕円曲線暗号は加法性(暗号文の加算ができる)が成り立ちます。
つまり、2個の$M$, $M'$とそれぞれ対応する乱数$r$, $r'$を使うと
\begin{align*}
Enc(M) &= (M + rQ, rP)\\
Enc(M') &= (M' + r'Q, r'P)
\end{align*}
ですが、このペアを要素ごとに足してみます。
\begin{align*}
Enc(M) + Enc(M') &= ((M + rQ) + (M' + r'Q), rP + r'P)\\
&=(M + M' + (r + r')Q, (r + r')P).
\end{align*}
これはよく見ると$M + M'$を乱数$r + r'$で暗号化したものとみなせます。
つまり
$Enc(M) + Enc(M') = Enc(M + M')$.
これが加法準同型暗号のアイデアです。
実はここまでのアイデアは20年ほど前から知られていました。
この2個の暗号文は「掛けられるよ」ということに気がついたのが今回のメインアイデアです。
lifted-ElGamal暗号
乗法性の説明をする前に加法性の補足をします。
暗号文が$M + M'$の形は何かと不便なので次のようなトリックを使います。
平文を整数$m$, $m'$に対して$M = mP$, $M' = m'P$とすると
$Enc(mP) + Enc(m'P) = Enc((m + m')P)$
となります。
こうすると歯車(=楕円曲線の点)ではなく整数$m$の和として扱えるので便利です。
この方法をlifted-ElGamal暗号といい、以降
$Enc(m) = (mP + rQ, rP) = ((m + rs)P, rP)$
とします。
ただしlifted-ElGamal暗号には一つ(大きな)欠点があります。
復号した結果は$mP$の形になるので$mP$から$m$を求めなくてはいけません。
楕円曲線暗号はこれができない(=離散対数問題が難しい)というのが前提でしたから困ったことになります。
ただ$m$が大きくないときは$P$, $2P$, $3P$, $4P$, ...と事前計算しておき、$mP$に一致する$m$を探すのは困難ではありません。したがってlifted-ElGamal暗号では平文は大きくない(高々32~40bit整数程度)という制約下で使います。
ペアリング
乗法性を説明するために準備をします。
lifted-ElGamal暗号のための歯車(=楕円曲線)を2個用意します。
その2個の歯車のそれぞれの歯車一つ分を$P$, $P'$とします。
さらにその2個の歯車から別のより複雑な歯車を作ります(詳細は数学編で)。
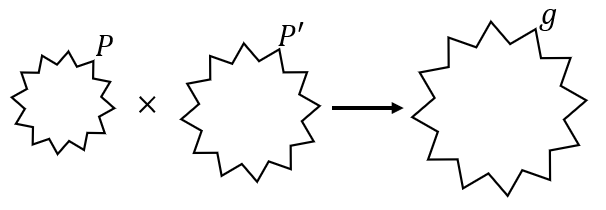
左個の歯車から右の歯車が決まる方法$e$があり、$P$と$P'$の行き先を$g$とします。
$g = e(P, P')$.
$g$を$P$と$P'$のペアリングと呼びます。
ペアリングには整数$a$, $b$に対して
$e(aP, bP') = abg$
という双線形性と呼ばれる性質が成り立ちます(知っている人への注意:ここでは右側の群も加法群として表記してます)。詳細はクラウドを支えるこれからの暗号技術を参照ください。
暗号文の積
準備が整ったので暗号文の積を作りましょう。
一つ目の歯車への暗号文を$Enc1(m) = (mP + rQ, rP) = (S1, T1)$,
二つ目の歯車への暗号文を$Enc2(m') = (m'P' + r'Q', r'P') = (S2, T2)$
とします。ここで$s$, $s'$が秘密鍵で$Q = sP$, $Q' = s'P'$とします。
それぞれの暗号文は2個の要素があるので4パターンのペアリングをとります。
$Enc1(m) × Enc2(m') = (S1, T1) × (S2, T2) := (e(S1, S2), e(S1, T2), e(T1, S2), e(T1, T2)).$
暗号文同士を掛けると要素が4個になったことに注意してください。
暗号文の復号
掛け算した暗号文はどうやって復号するのでしょうか。
次のようにします。計算が多いですが、一つ一つは難しくありません。注意深く追ってみてください。
まず
\begin{align*}
(S1, T1) &= ((m + rs)P, rP)\\
(S2, T2) &= ((m' + r's')P', r'P')
\end{align*}
に注意すると
\begin{align*}
a &:= e(S1, S2) = e((m + rs)P, (m' + r's')P') = (m + rs)(m' + r's')g.\\
b &:= e(S1, T2) = e((m + rs)P, r'P') = (m + rs)r'g.\\
c &:= e(T1, S2) = e(rP, (m' + r's')P') = (m' + r's')rg.\\
d &:= e(T1, T2) = e(rP, r'P') = rr'g.
\end{align*}
よって秘密鍵$s$, $s'$を使うと
\begin{align*}
a + (ss')d - s'b - sc &= ((m + rs)(m' + r's') + rr'ss' - (m + rs)r's - (m' + r's')rs')g\\
&= mm'g.
\end{align*}
きれいに乱数$r$, $r'$が消えて$mm'g$だけが残りました。右端の歯車に関する(小さな)離散対数問題を解くことで$mm'$を得られます。
これは元の平文$m$, $m'$の積となっています。つまり暗号文同士の積が実現できました。
乗算後の加算
2個の暗号文を掛けたら4個の要素になりました。その暗号文はまた加算ができるのでしょうか?
はい、暗号文の要素ごとに足すと足した暗号文になります。簡単ですね。
一般に乗算後の暗号文は$r_1$, $r_2$, $r_3$を乱数として
$Enc_{G_T}(m)=(a, b, c, d) = ((m + r_1 s' + r_2 s - r_3 ss')g, r_1 g, r_2 g, r_3 g)$
という形をしています。実際上記の暗号文の復号と同じく
$a + (ss')d - s'b - sc = (m + r_1 s' + r_2 s - r_3 ss' + (ss')r3 - s' r_1 - s r_2)g = mg$
で復号できます。
従って$m$, $m'$の暗号文$Enc_{G_T}(m)$, $Enc_{G_T}(m')$に対してそれらを成分ごとに足すと
\begin{align*}
Enc_{G_T}(m) + Enc_{G_T}(m') &= ((m + r_1 s' + r_2 s - r_3 ss')g + (m' + r'_1 s' + r'_2 s - r'_3 ss')g, r_1 g + r'_1 g, r_2 g + r'_2 g, r_3 g + r'_3 g)\\
&=(((m + m') + (r_1 + r'_1)s' + (r_2 + r'_2) s - (r_3 + r'_3)ss')g, (r_1 + r'_1)g, (r_2 + r'_2)g, (r_3 + r'_3)g)\\
&=(((m + m') + r''_1 s' + r''_2 s - r''_3 ss)g, r''_1 g, r''_2 g, r''_3 g) \quad \text{ここで } r''_i = r_i + r'_i\text{ と置いた}\\
&= Enc_{G_T}(m + m')
\end{align*}
となるからです。
まとめ
古くからよく知られた加法準同型暗号の一つであるlifted-ElGamal暗号を紹介しました。
2種類のlifted-ElGamal暗号の要素をペアリングを用いて「掛け算」することで一度だけ乗算可能なL2準同型暗号を構築しました。この方式は現在知られているL2準同型暗号の中で一番コンパクトです。
次回は準同型暗号の最前線3(理論編)です。