初めに
BLS署名はBLS署名の紹介と実装で書いたように、公開鍵や署名の整数倍しか使わない署名方式でした。
そのため秘密分散と呼ばれる技術と相性がよく、分散された署名は多数決で物事を決める投票のような役割を担えます。
ブロックチェーンを使ったEthereumというプラットフォームのトランザクションを高速化するプロジェクトDFINITYで使われています。
秘密分散
(k, n)閾値秘密分散とはあるデータsをn個に分割し、そのうちk個集めれば元のsを復元できるという手法です。
やり方は次の通りです。
定数項はsで、他の係数をランダムに選んだ(k - 1)次多項式を用意します。
f(x) = s + r_1 x + r_2 x^2 + ... + r_{k-1} x^{k-1}
すると$f(0) = s$です。
n人のユーザに対して、相異なる値$x_1, ..., x_n$を決めてi番目のユーザに$f(x_i)$を渡します($x_i$はみなに公開してよい。$f(x_i)$はi番目のユーザ以外には秘密にします)。
$(f(x_1), ..., f(x_n))$がsの秘密分散です。
異なる$k$個の点を通る(k - 1)次はただ一つ決まるので、n個に秘密分散された値のうちk個が集まれば元の多項式が復元できます。つまり$f(0) = s$が求まるという仕組みです。
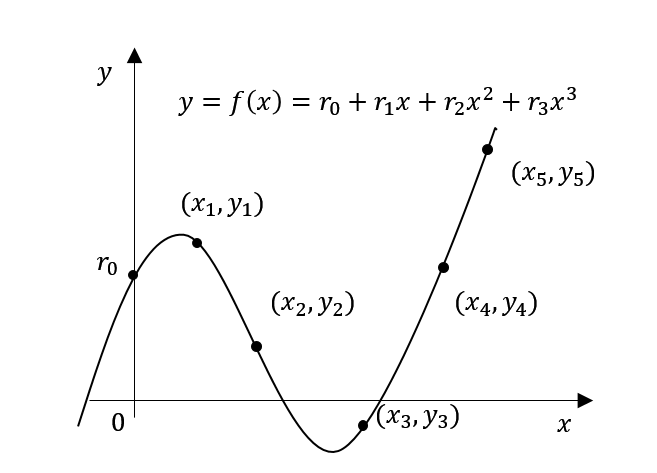
グラフはk = 4のときの図で3次曲線が書かれています(『クラウドを支えるこれからの暗号技術』11.3の図11.2の引用)。
$(x_1, y_1), ..., (x_5, y_5)$のうちどれか3個決めるとその点を通る3次曲線が決まるので$r_0 = s$が決まります。
sの復元方法の細かいことはここでは紹介しませんが$\{y_i\}$の線形和で求まる
ことが重要です。
s = (なんとか) \times y_1 + (かんとか) \times y_2 + ...
BLS署名に秘密分散を適用
BLS署名を復習します。$e:G_1 \times G_2 \rightarrow G_T$をペアリング、$H : \{文字列\} \rightarrow G_1$をハッシュ関数、QをG2の元としたとき、
- 秘密鍵sの公開鍵はsQ
- メッセージmの署名 s H(m)
でした。どちらもある値Q, H(m)をs倍している形です。
したがって秘密鍵sを秘密分散$f(x_1), ...$するとi番目のユーザの秘密鍵は$f(x_i)$, 対応する公開鍵は$f(x_i)Q$, メッセージmの署名は$f(x_i) H(m)$になります。
そして前節で記したようにそれらの線形和なので、秘密鍵だけでなく公開鍵や署名も同じ線形和で復元できます!
たとえばs, s'を秘密鍵とすると対応する公開鍵はsQ, s'Qで署名はsH(m), s'H(m)です。
そこで2個の公開鍵から3(sQ) + 4(s'Q) = (3s + 4s')Qを作ると、これは秘密鍵(3s + 4s')に対応する公開鍵であり、署名も3sH(m) + 4s'H(m) = (3s + 4s')H(m)と対応する署名となります。sやs'を知らなくても公開鍵や署名を計算できることに注意してください。
これはつまり次のことができます。
BLS署名のマスター秘密鍵sを一つ決めてn人に秘密分散し、各ユーザに分散された秘密鍵を配布します。そこでsは破棄してもかまいません。
すると各ユーザは、あるメッセージmに対して通常のBLS署名をつけられます。もちろんだれでもその正当性を検証できます。
そして、n人のうちk人が作った署名を集めればメッセージmに対するsによる署名を構築できます。
k人が結託して秘密鍵を共有することなく、署名を公開するだけならsは復元できません。また署名に乱数が入っていないので完全に同じ署名が復元できます。
blsで実装したので興味ある方はごらんください。
このアイデアをブロックチェーンの中で十分な人数の署名が集まったときに次のステップに進む多数決の仕組みとして利用します。
冒頭で紹介したDFINITYではEthereumのトランザクションより50倍速いとあります(私は未確認ですが)。
面白いですね。