初めに
ペアリング暗号で使われるペアリングの性質を紹介します。
そしてその性質をペアリング暗号ライブラリmclを使って確認します。
mclのインストール方法はペアリング暗号ライブラリmclを使ってみるを参照してください。
ペアリング
巡回群
ペアリングの説明の前に巡回群という言葉を紹介します。
歯車を思い浮かべ、時計回りに12時の方向から0, P, 2P, 3P, ...と名前をつけます。歯の数がr個あったとするとrPは0と同じ位置になります。
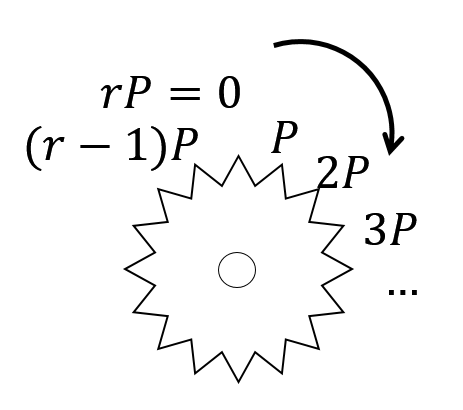
このときa, bを整数としてaPの位置からbだけ時計回りにまわる操作をaP + bPと書きます。するとaP + bP = ((a + b) % r)Pという関係式が成り立ちます(%はrで割った余り)。
この歯車のことをr個からなる(加法に関する)巡回群といいます。
別の巡回群を紹介します。$\mu$を1でない1のr乗根とします。$\mu^r = 1$。
集合X=$\{\mu^i | i = 0, 1, ..., r-1\}$を考えます。X時計の3時の方向を1として反時計まわりに$\mu$, $\mu^2$, $\mu^3$, ...と続きます。

Xの2点$\mu^a$と$\mu^b$の掛け算は$\mu^a \times \mu^b = \mu^{a+b}$です。これを(乗法に関する)巡回群といいます。
実際のところ加法と乗法の表記の違いは重要ではなく、ぐるぐる回っているというイメージの方が本質です。どちらを使うかはとりあえず慣習的なものととらえてください。
ペアリング
巡回群の説明が終わったのでペアリングの紹介をします。
正の整数rを一つ決めます。G1, G2を加法に関するr個の巡回群、GTを乗法に関するr個の巡回群とします。歯車が3個登場するわけです。
G1の歯車の位置をaP, G2の歯車の位置をbQとしたとき(G2はG1と異なる歯車なので
PでなくQとした)、行き先が$\mu^{ab}$となる写像をペアリングといいます。

\begin{array}{cccc}
e:& G_1 \times G_2 & \longrightarrow & G_T \\
&(aP,bQ) & \longmapsto & \mu^{ab}
\end{array}
aやbの値を2倍、3倍とすると行き先が2乗、3乗されます。
e(2aP, bQ) = \mu^{2ab},\\
e(aP, 3bQ) = \mu^{3ab}
この様な性質を双線形性といいます。
mclライブラリの基本クラスと演算
mclライブラリの初期化
ペアリング演算には様々なパラメータやデータ構造が必要です。
mclライブラリはそのあたりを隠した最小限の設定で使えるようになっています。
# include <mcl/bn256.hpp>
using namespace mcl::bn256;
bn256init();
mcl::bn256::bn256init()は全ての演算の前に呼ぶ必要があるので注意してください。以降using namespace mcl::bn256;したと仮定します。
巡回群G1, G2, GTに対応するmclのクラスとしてG1, G2, Fp12があります。ペアリング写像は
void BN::pairing(Fp12& e, const G1& P, const G2& Q);
と定義されています。
G1, G2の点P, Qの設定
G1, G2の点PやQを決めるにはある関係式を満たしたパラメータを渡す必要があります。ここでは天下り的に値を設定します。
G1 P(-1, 1);
const char *aa = "12723517038133731887338407189719511622662176727675373276651903807414909099441";
const char *ab = "4168783608814932154536427934509895782246573715297911553964171371032945126671";
const char *ba = "13891744915211034074451795021214165905772212241412891944830863846330766296736";
const char *bb = "7937318970632701341203597196594272556916396164729705624521405069090520231616";
G2 Q(Fp2(aa, ab), Fp2(ba, bb));
Pは簡単ですが、Qはやたら複雑ですね。申し訳ないですがここはそういうものだと思ってコピペしてください。
G1, G2の点の整数倍
点Pのa倍aPを計算するにはG1::mulやG2::mulを使います。
G1 P1;
G2 Q2;
G1::mul(P1, P, 123); // P1 = 123 P
G2::mul(Q1, Q, 456); // Q1 = 456 Q
なお、G1::mul(P1, 123, P)とはかけないので注意してください。
G1やG2の点の値を表示するにはoperator<<()を使います。
値を表示するととても大きな数が複数出るのに驚かれるかもしれません。
実は歯車の数rはここではr = 16798108731015832284940804142231733909759579603404752749028378864165570215949 というとても大きな素数です。G1やG2の構造の詳細はここでは触れません。
Fp12の元の巾乗
行き先の巡回群は乗法に関するものだったので巾乗(power)になります。
Fp12 y;
Fp12::pow(y, x, 12345); // y = x^12345
Fp12の構造についても今回は触れません。データとしては整数が12個ならんだものです。
ペアリングの双線形性の確認
それでは双線形を確認しましょう。
点P, Qに対してまずペアリングe1 = e(P, Q)を求め、Pをa倍、Qをb倍した点aP, bQのペアリングe2 = e(aP, bQ)が元のeのab乗になっていることをみます。
const int a = 123;
const int b = 456;
G1 aP;
G2 bQ;
G1::mul(aP, P, a); // aP = P x a
G2::mul(bQ, Q, b); // bQ = Q x b
Fp12 e1, e2;
BN::pairing(e1, P, Q); // e1 = e(P, Q)
BN::pairing(e2, aP, bQ); // e2 = e(aP, bQ)
Fp12 e3;
Fp12::pow(e3, e1, a * b); // e3 = e1^(ab)
printf("%s\n", e2 == e3 ? "ok" : "ng");
このコードを実行してokが表示されることを確認してみましょう。
なお、aやbを大きくしてa * bがintの範囲を超えると値がおかしくなるので注意してください。
その場合は大きな値を扱えるGMPのmpz_classを使います。
mpz_class a = "12341298471298374198327419827389127487";
mpz_class b = "283749283742983742987429847298748297429837423";
G1::mul(aP, P, a);
G2::mul(bQ, Q, b);
Fp12::pow(e1, e, a * b); // e1 = e^(a b)
まとめ
ペアリングの双線形性とmclライブラリでその性質を確認する方法を紹介しました。
次回はBLS署名などを紹介したいと思います。