はじめに
今回は前回作成したブロードウェイ・ミュージカルの平均単価の予測モデルについて、ニューラルネットワークを用いたモデルの構築を行っていきたいと思います。
前回の内容は以下をご参照ください。
前回はSARIMAモデルを用いて分析と予測を行ったのですが、季節変動周期が大きかったこともあり、データとして提供されている「週ごと」のモデルではなく、「年ごと」に短縮したものを作成しました。
そこで、今回はLSTMを用いたニューラルネットワークモデルを構築することで、週ごとのモデルを構築し、精度の検証までを行っていきたいと思います。
目的・環境
目的
ブロードウェイで上演されるミュージカル全体の過去実績から、平均単価の値上がりを予測するモデルをニューラルネットワークで構築し、精度評価を行う
環境
・言語:Python3
・OS:Windows 11
・Chrome
・Google Colaboratory
※前回と同様の環境で行います。
使用データ
引き続きkaggle「Broadway Show」のデータを使用させていただいております。
※データの詳細については前回を参照いただけますと幸いです。
実践してみる
0.データの準備
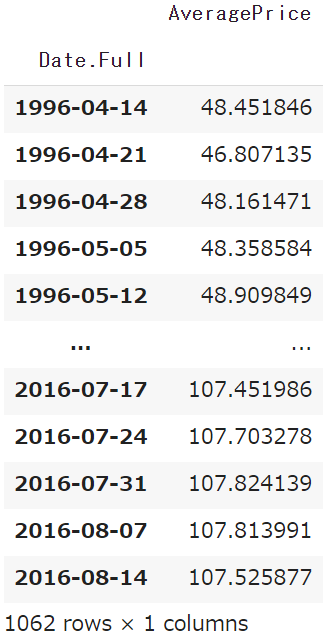
前回も行った処理をおこない、日付データと平均単価のDataFrameを作ります。
※それぞれの細かい内容は前回の記事を参照してください。
※今回も他の特徴量は一旦無視をし、時系列と平均単価だけのモデルを構築していければと思います。
#1.データの読み込み
bw_data=pd.read_csv('/content/drive/MyDrive/Colab Notebooks/broadway/broadway.csv')
#2.不要な特徴量の削除+日付形式の変換
musical_data=bw_data[bw_data['Show.Type']=='Musical'] #Show.TypeのうちMusicalだけを抽出
drop_col = ['Date.Day','Date.Month','Date.Year','Show.Theatre','Statistics.Capacity', 'Statistics.Gross Potential','Statistics.Performances']
musical_data=musical_data.drop(drop_col,axis=1) #drop_colで指定したカラムを削除
musical_data['Date.Full']=pd.to_datetime(musical_data['Date.Full']) #Date.Fullの形式を日付形式に変換
#3.データの成形
#3-1.週ごとでグループ化し、データをまとめ、合計値を出す
musical_data=musical_data.groupby('Date.Full').sum()
#3-2.日付順にソートをし直す
musical_data=musical_data.sort_index(ascending=True)
musical_data=musical_data.reset_index() #indexの振り直し1
#3-3.連続する外れ値とみなした264件のデータを削除(外れ値の測定は省略)
musical_data=musical_data.drop(range(264))
musical_data=musical_data.reset_index() #indexの振り直し2
musical_data=musical_data.drop('index',axis=1) #一回目のindex振り直しが「index」カラムとして残ってしまっているため削除
#3-4.平均単価を入れるカラム追加し、一人あたりの平均単価を計算
musical_data['AveragePrice']=musical_data['Statistics.Gross']/musical_data['Statistics.Attendance']
del musical_data['Statistics.Attendance']
del musical_data['Statistics.Gross']
musical_avg_data=musical_data.set_index('Date.Full')
#3-5.出力し確認
musical_avg_data
1.データセットの作成
LSTMを用いたモデル構築を行っていくにあたり、時系列データから、その値のみを取り出していきます。
#値のみ取り出す
dataset = musical_avg_data.values
#データをfloat型に変換
dataset = dataset.astype('float32')
#出力し内容の確認
dataset
LSTMに適用させるため、float型への変換も合わせて行っています。
>>>出力結果
array([[ 48.451847],
[ 46.807137],
[ 48.161472],
...,
[107.82414 ],
[107.81399 ],
[107.52588 ]], dtype=float32)
2.データの分割
今作成したデータセットを、
- モデルに学習させるための訓練データ
- モデルの精度を確認するための検証データ
の2つに分割していきます。
時系列データのため、ランダムな分割ではなく連続性を残した状態で分割していきます。今回は頭から80%を訓練データ、残りの20%を検証データとしていきたいと思います。
# 訓練データにするデータ件数を算出
train_size = int(len(dataset) * 0.8)
# 訓練データ、検証データに分割
train, test = dataset[0:train_size, :], dataset[train_size:len(dataset), :]
# 確認用
print(len(dataset), len(train), len(test))
>>>出力結果
1062 849 213
# 全体の個数1062に対し、訓練用が8割、学習用が2割になっています
3.データのスケーリング
正規化によりデータのスケーリングを行っていきます。
# 最小値が0, 最大値が1となるようにスケーリング方法を定義
scaler = MinMaxScaler(feature_range=(0, 1))
# `train`のデータを基準にスケーリングするようパラメータを定義
scaler_train = scaler.fit(train)
# パラメータを用いて`train`データをスケーリング
train = scaler_train.transform(train)
# パラメータを用いて`test`データをスケーリング
test = scaler_train.transform(test)
4.入力データ・正解ラベルの作成
スケーリングしたデータから、入力データ(=X)、正解ラベル(=Y)を作成していきます。
trainとtestの2回分作成するため、関数として(ここではcreate_dataset()として)定義をしていきます。
def create_dataset(dataset, look_back):
data_X, data_Y = [], []
for i in range(look_back,len(dataset)):
data_X.append(dataset[i-look_back:i, 0])
data_Y.append(dataset[i, 0])
return np.array(data_X), np.array(data_Y)
# 入力データが何期=何週分のデータを取るかを定義
look_back = 3
# 作成した関数`create_dataset`を用いて、入力データ・正解ラベルを作成
train_X, train_Y = create_dataset(train, look_back)
test_X, test_Y = create_dataset(test, look_back)
関数の中身としては、以下の通りです(自分の理解のために言語化しようと試みたのですがうまく伝わりづらい内容で恐れ入ります…)。
-
look_back(基準点から何期前までのデータを利用するか) -
data_X,data_Yのリスト(空)を用意 -
data_Xにはdatasetのインデックスi-look_back~i数分の数値をリストとして格納していく(→look_back数分のリスト) -
data_Yにはdatasetのインデックスiの数値を格納していく - これらを
look_back~datasetの最後まで繰り返していく
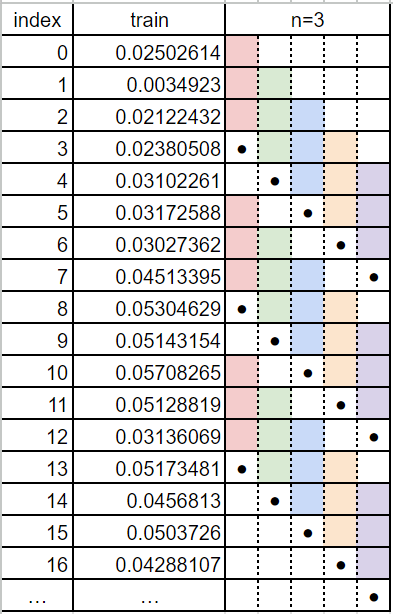
上記の表ではlook_back=3で、
- ●が基準点=正解ラベル=
train_Y - それぞれ色が付いている箇所が入力データ=
train_X
をそれぞれリスト化している、という関数のつくりになります。
それぞれの出力結果は下記の通りですので見比べてもこの通りになっています。
train
shape:(849, 1)
[[0.02502614]
[0.0034923 ]
[0.02122432]
[0.02380508]
[0.03102261]
[0.03172588]
[0.03027362]
[0.04513395]
[0.05304629]
[0.05143154]
[0.05708265]
[0.05128819]
[0.03136069]
[0.05173481]
[0.0456813 ]
[0.0503726 ]
[0.04288107]
[0.05268753]
[0.05465895]
[0.0457989 ]
[0.04272509]
[0.07561064]
[0.04109555]
[0.04885834]
[0.04976779]
[0.05531418]
[0.06562603]
[0.06613487]
[0.05446428]
[0.05543637]
[0.05121708]
[0.05309761]
[0.04277307]
[0.10968715]
[0.07820207]
[0.0767827 ]
[0.06629646]
[0.16126555]
[0.12621939]
[0.05119461]
[0.03338242]
[0.03414828]
[0.00957149]
[0.03263533]
[0.05339915]
[0.02484387]
[0.01161325]
[0.00200593]
[0.01138395]
[0.02554029]
[0.04895431]
[0.03807372]
[0.02062756]
[0.0154568 ]
[0.01590681]
[0.02791274]
[0.02735269]
[0.04096019]
[0.03589272]
[0.02912009]
[0.04779804]
[0.03241366]
[0.02944213]
[0.03430766]
[0.01269531]
[0.04131424]
[0.04561275]
[0.0444417 ]
[0.06222981]
[0.06027091]
[0.06683141]
[0.0583787 ]
[0.06367064]
[0.06087917]
[0.05638546]
[0.04805213]
[0.0325073 ]
[0.03921735]
[0.03834468]
[0.03973389]
[0.04760766]
[0.0400005 ]
[0.03318459]
[0.04373682]
[0.05061489]
[0.11348236]
[0.06625718]
[0.067204 ]
[0.04159379]
[0.13865781]
[0.15187544]
[0.01841801]
[0.01296431]
[0.0191946 ]
[0. ]
[0.03205788]
[0.05170709]
[0.03021151]
[0.0359363 ]
[0.04743361]
[0.04062575]
[0.06267166]
[0.06871426]
[0.06362879]
[0.08524656]
[0.0883559 ]
[0.07535374]
[0.07738322]
[0.07902771]
[0.07747477]
[0.07297075]
[0.06051964]
[0.06934726]
[0.06946731]
[0.0843156 ]
[0.08916569]
[0.06445265]
[0.08605701]
[0.08041549]
[0.07751596]
[0.0773887 ]
[0.07991475]
[0.08395034]
[0.08094996]
[0.08142078]
[0.093463 ]
[0.09198755]
[0.10336596]
[0.09321791]
[0.07594323]
[0.08135563]
[0.07553017]
[0.04866445]
[0.02504271]
[0.05239832]
[0.0586803 ]
[0.05203778]
[0.12791038]
[0.09577066]
[0.09558219]
[0.09578508]
[0.17164493]
[0.21298999]
[0.03146422]
[0.02000684]
[0.03368282]
[0.02206904]
[0.0276376 ]
[0.07233953]
[0.04360646]
[0.03332233]
[0.04601586]
[0.05868185]
[0.08100933]
[0.08031625]
[0.09417981]
[0.08421832]
[0.06971997]
[0.0718779 ]
[0.05960423]
[0.06592184]
[0.07434797]
[0.07424688]
[0.05336249]
[0.06853324]
[0.07270408]
[0.08315229]
[0.09463751]
[0.05335909]
[0.0908969 ]
[0.09512329]
[0.08785361]
[0.08976018]
[0.08435434]
[0.08913296]
[0.08381081]
[0.08432609]
[0.10472298]
[0.0985986 ]
[0.0907439 ]
[0.09017849]
[0.08923775]
[0.1000483 ]
[0.0949443 ]
[0.09798914]
[0.08653367]
[0.08831507]
[0.09684217]
[0.07430595]
[0.16116196]
[0.11657226]
[0.1147424 ]
[0.1055246 ]
[0.16305876]
[0.19989055]
[0.09251314]
[0.11429912]
[0.11146176]
[0.08868146]
[0.09490699]
[0.11580795]
[0.12179691]
[0.10142392]
[0.10373527]
[0.10427195]
[0.10532457]
[0.10889518]
[0.1128608 ]
[0.10858727]
[0.11134827]
[0.15144092]
[0.13759512]
[0.12894458]
[0.13912773]
[0.13647884]
[0.12963891]
[0.13039225]
[0.13749033]
[0.14049989]
[0.14742929]
[0.10658443]
[0.1116004 ]
[0.13513565]
[0.12752867]
[0.12900126]
[0.1284669 ]
[0.13254756]
[0.1306572 ]
[0.12794101]
[0.1331523 ]
[0.14371604]
[0.13458335]
[0.14357698]
[0.1413911 ]
[0.15500301]
[0.14933383]
[0.15303028]
[0.13621032]
[0.14334375]
[0.14723796]
[0.14965647]
[0.22281337]
[0.17005306]
[0.18671739]
[0.18411511]
[0.18996602]
[0.31451958]
[0.15261698]
[0.14136636]
[0.14481282]
[0.14426798]
[0.12076902]
[0.13156968]
[0.1699472 ]
[0.13584834]
[0.12285781]
[0.12325066]
[0.11768788]
[0.14312804]
[0.12966347]
[0.12654543]
[0.14827979]
[0.14439839]
[0.12591445]
[0.14221102]
[0.12810874]
[0.14931911]
[0.15357113]
[0.14263618]
[0.15286553]
[0.17623997]
[0.17829126]
[0.16209275]
[0.12943578]
[0.1635825 ]
[0.16691726]
[0.16248941]
[0.17959946]
[0.18024546]
[0.17197752]
[0.17583787]
[0.17739284]
[0.16693681]
[0.11243623]
[0.13554513]
[0.15311623]
[0.16751206]
[0.15759355]
[0.15739197]
[0.13999206]
[0.14337987]
[0.18085277]
[0.17847568]
[0.26671988]
[0.2247954 ]
[0.21978688]
[0.20146883]
[0.21103162]
[0.3453591 ]
[0.22662759]
[0.20908386]
[0.23053497]
[0.22460967]
[0.21735048]
[0.21898037]
[0.25925958]
[0.21916693]
[0.21205044]
[0.2147159 ]
[0.22357982]
[0.19446886]
[0.24122667]
[0.25258595]
[0.23530155]
[0.23225129]
[0.2341333 ]
[0.23865652]
[0.2395792 ]
[0.24261749]
[0.24640179]
[0.22088009]
[0.25096613]
[0.2525633 ]
[0.24716812]
[0.2503726 ]
[0.21061015]
[0.25215572]
[0.23955351]
[0.23569173]
[0.23692882]
[0.23378778]
[0.2347104 ]
[0.23378909]
[0.23631573]
[0.23477703]
[0.21299672]
[0.24368286]
[0.24352568]
[0.24667418]
[0.24982303]
[0.24822599]
[0.25453323]
[0.2540291 ]
[0.27752805]
[0.27410322]
[0.27445108]
[0.35099626]
[0.3153084 ]
[0.3074466 ]
[0.31877398]
[0.41279542]
[0.3723023 ]
[0.2681588 ]
[0.28050238]
[0.23934865]
[0.2839983 ]
[0.24766368]
[0.2872265 ]
[0.26790696]
[0.26204735]
[0.17439169]
[0.2538151 ]
[0.25617862]
[0.25707603]
[0.25979614]
[0.25577617]
[0.26985395]
[0.26588273]
[0.24143696]
[0.26930183]
[0.25875127]
[0.24779844]
[0.23824131]
[0.25097895]
[0.2542495 ]
[0.2729568 ]
[0.27808517]
[0.22996134]
[0.27918434]
[0.27707058]
[0.27320242]
[0.27377254]
[0.27873933]
[0.2927454 ]
[0.2806518 ]
[0.28658116]
[0.25322384]
[0.24947709]
[0.26539743]
[0.26456797]
[0.27291077]
[0.29922158]
[0.2844544 ]
[0.28038663]
[0.2729683 ]
[0.2922625 ]
[0.28184712]
[0.28520548]
[0.37510288]
[0.34318328]
[0.32724917]
[0.31278068]
[0.42240858]
[0.42963552]
[0.29595423]
[0.307324 ]
[0.2976634 ]
[0.28231508]
[0.25331897]
[0.31515247]
[0.26604724]
[0.2599706 ]
[0.26265484]
[0.2503656 ]
[0.27110207]
[0.27458364]
[0.27708822]
[0.276291 ]
[0.26639533]
[0.25920528]
[0.25688434]
[0.26347655]
[0.25542635]
[0.25196058]
[0.23996127]
[0.25348955]
[0.2771018 ]
[0.27625567]
[0.28393883]
[0.24327934]
[0.27309048]
[0.28277338]
[0.2867338 ]
[0.28967685]
[0.28540558]
[0.2805786 ]
[0.28281105]
[0.27360332]
[0.2726066 ]
[0.32427615]
[0.2577905 ]
[0.24921316]
[0.2527899 ]
[0.27239174]
[0.25745118]
[0.25190902]
[0.24290574]
[0.2795834 ]
[0.27516508]
[0.2727751 ]
[0.3629216 ]
[0.31941646]
[0.30821562]
[0.31617934]
[0.36389583]
[0.42113793]
[0.2594359 ]
[0.2786746 ]
[0.24253035]
[0.24806243]
[0.24568498]
[0.267066 ]
[0.30413252]
[0.26897353]
[0.24091834]
[0.24580127]
[0.24742168]
[0.29576445]
[0.29738635]
[0.25617433]
[0.2607051 ]
[0.26541102]
[0.25956315]
[0.26494414]
[0.27853483]
[0.28267187]
[0.2841227 ]
[0.2819233 ]
[0.296268 ]
[0.29833984]
[0.30373007]
[0.30070204]
[0.31147474]
[0.31756055]
[0.3170182 ]
[0.3122424 ]
[0.32684678]
[0.32724863]
[0.322115 ]
[0.31295848]
[0.31221402]
[0.28895038]
[0.28367442]
[0.26137316]
[0.28923357]
[0.3032781 ]
[0.30837065]
[0.3112409 ]
[0.30136555]
[0.30546248]
[0.32382834]
[0.3276466 ]
[0.46497464]
[0.3828706 ]
[0.3979993 ]
[0.39367008]
[0.43090093]
[0.57964635]
[0.3820684 ]
[0.39120817]
[0.38537866]
[0.380628 ]
[0.32725245]
[0.34871197]
[0.38178682]
[0.3647622 ]
[0.33625412]
[0.34620035]
[0.36798495]
[0.37415153]
[0.34636295]
[0.32347918]
[0.37518346]
[0.34385353]
[0.3017311 ]
[0.3235674 ]
[0.33758223]
[0.35097426]
[0.3427006 ]
[0.36457348]
[0.37002456]
[0.39584935]
[0.39217532]
[0.39778042]
[0.39730906]
[0.41000438]
[0.41319633]
[0.41373253]
[0.4168948 ]
[0.41615176]
[0.41306055]
[0.41023946]
[0.4188255 ]
[0.41469467]
[0.40262067]
[0.41095018]
[0.420357 ]
[0.4411347 ]
[0.42617273]
[0.4197259 ]
[0.39035487]
[0.3885066 ]
[0.4145515 ]
[0.40718806]
[0.54886377]
[0.44413865]
[0.43839085]
[0.45436084]
[0.5045612 ]
[0.6314254 ]
[0.4119451 ]
[0.41329372]
[0.38737285]
[0.38495702]
[0.33678925]
[0.3691935 ]
[0.43968093]
[0.3803631 ]
[0.36547548]
[0.3596804 ]
[0.36043876]
[0.37673038]
[0.37449068]
[0.42373264]
[0.40112698]
[0.37705874]
[0.35835296]
[0.3640992 ]
[0.37732583]
[0.38723338]
[0.3764714 ]
[0.36331737]
[0.37724203]
[0.38594854]
[0.4035486 ]
[0.3938731 ]
[0.38519013]
[0.43583894]
[0.44315064]
[0.45545018]
[0.47120702]
[0.47178555]
[0.4560722 ]
[0.44470417]
[0.4526795 ]
[0.42386413]
[0.3900144 ]
[0.41063368]
[0.41430235]
[0.45591712]
[0.45053387]
[0.4734025 ]
[0.45310044]
[0.40982902]
[0.42201996]
[0.62515604]
[0.68869495]
[0.51969194]
[0.48238075]
[0.47657955]
[0.535686 ]
[0.7041838 ]
[0.48722327]
[0.4055487 ]
[0.43465245]
[0.3971895 ]
[0.37669533]
[0.36562502]
[0.41208124]
[0.38336515]
[0.34763825]
[0.34050214]
[0.35741037]
[0.39801157]
[0.3971548 ]
[0.3664527 ]
[0.3631217 ]
[0.3807991 ]
[0.36365432]
[0.39154446]
[0.37076157]
[0.3822567 ]
[0.38518518]
[0.37649006]
[0.37849855]
[0.3732537 ]
[0.39138973]
[0.41723073]
[0.3783326 ]
[0.44269907]
[0.44895148]
[0.45518208]
[0.46853483]
[0.47983527]
[0.47718787]
[0.4606849 ]
[0.47573364]
[0.4019934 ]
[0.38460928]
[0.40625906]
[0.38370568]
[0.40007448]
[0.44524848]
[0.4362569 ]
[0.44129777]
[0.42840743]
[0.44080877]
[0.42896044]
[0.41651177]
[0.63164556]
[0.5106875 ]
[0.4926597 ]
[0.4967116 ]
[0.6614512 ]
[0.63127136]
[0.41607153]
[0.4645145 ]
[0.42290032]
[0.40719926]
[0.3656633 ]
[0.46453035]
[0.4368037 ]
[0.3915404 ]
[0.40615582]
[0.40768647]
[0.41686785]
[0.4074298 ]
[0.42554843]
[0.5032058 ]
[0.4968593 ]
[0.41677952]
[0.39219868]
[0.40452433]
[0.42329156]
[0.42935717]
[0.4973601 ]
[0.520337 ]
[0.54870665]
[0.5806416 ]
[0.6012964 ]
[0.5343671 ]
[0.5879284 ]
[0.61513925]
[0.61601067]
[0.6022514 ]
[0.6310798 ]
[0.640046 ]
[0.61407113]
[0.6006274 ]
[0.5697825 ]
[0.5441599 ]
[0.53212535]
[0.5163621 ]
[0.520661 ]
[0.553105 ]
[0.5286294 ]
[0.48162007]
[0.4355526 ]
[0.4972142 ]
[0.48914087]
[0.4854225 ]
[0.7618512 ]
[0.6295136 ]
[0.6080104 ]
[0.5947943 ]
[0.7705176 ]
[0.80724275]
[0.5234815 ]
[0.53957295]
[0.50877106]
[0.4936577 ]
[0.4548217 ]
[0.5852699 ]
[0.5245849 ]
[0.4406501 ]
[0.44883704]
[0.47721076]
[0.48322952]
[0.4917451 ]
[0.55852723]
[0.5360124 ]
[0.48000896]
[0.47166705]
[0.49641228]
[0.50546 ]
[0.51512635]
[0.52145946]
[0.51673305]
[0.5225092 ]
[0.5320723 ]
[0.5602486 ]
[0.55347633]
[0.52746475]
[0.56462324]
[0.58124757]
[0.5756283 ]
[0.57236886]
[0.5835146 ]
[0.5745715 ]
[0.5600463 ]
[0.5416546 ]
[0.55585027]
[0.48987508]
[0.49237514]
[0.50569725]
[0.49848998]
[0.54686713]
[0.5002457 ]
[0.5083971 ]
[0.44955313]
[0.4764521 ]
[0.5052068 ]
[0.53641176]
[0.72663784]
[0.6194565 ]
[0.60785604]
[0.6094575 ]
[0.7373266 ]
[0.83010805]
[0.58855665]
[0.56729686]
[0.5457535 ]
[0.4969293 ]
[0.4473629 ]
[0.49508893]
[0.5869677 ]
[0.57742465]
[0.45357692]
[0.46955323]
[0.5016581 ]
[0.4512154 ]
[0.45280957]
[0.43442798]
[0.47744536]
[0.62240505]
[0.5364413 ]
[0.50953686]
[0.49155688]
[0.5515157 ]
[0.55041194]
[0.5250572 ]
[0.5397192 ]
[0.5581243 ]
[0.6151464 ]
[0.59002066]
[0.6108477 ]
[0.60503125]
[0.62597597]
[0.61851203]
[0.6333308 ]
[0.6291685 ]
[0.60309803]
[0.5466509 ]
[0.5832646 ]
[0.517396 ]
[0.55823433]
[0.55684745]
[0.57499874]
[0.6637217 ]
[0.65186214]
[0.6326506 ]
[0.61108565]
[0.60191894]
[0.6195426 ]
[0.5910344 ]
[0.80722487]
[0.66512215]
[0.6559496 ]
[0.6697364 ]
[0.7436224 ]
[1. ]
[0.6921803 ]
[0.6377411 ]
[0.59824586]
[0.54307234]
[0.5016414 ]
[0.5689379 ]
[0.69034994]
[0.6618624 ]
[0.5531596 ]
[0.58237886]
[0.6278132 ]
[0.6240814 ]
[0.65015244]
[0.73547316]
[0.7202023 ]
[0.6216053 ]
[0.6118895 ]
[0.63003385]
[0.6237917 ]
[0.66039157]
[0.6744511 ]
[0.67192984]
[0.69771504]
[0.70374286]
[0.7356286 ]
[0.74151945]
[0.7086481 ]
[0.72226715]]
train_X
Shape:(846, 3)
[[0.02502614 0.0034923 0.02122432]
[0.0034923 0.02122432 0.02380508]
[0.02122432 0.02380508 0.03102261]
...
[0.69771504 0.70374286 0.7356286 ]
[0.70374286 0.7356286 0.74151945]
[0.7356286 0.74151945 0.7086481 ]]
train_Y
Shape:(846, )
(846,)
[0.02380508 0.03102261 0.03172588 0.03027362 0.04513395 0.05304629
0.05143154 0.05708265 0.05128819 0.03136069 0.05173481 0.0456813
0.0503726 0.04288107 0.05268753 0.05465895 0.0457989 0.04272509
0.07561064 0.04109555 0.04885834 0.04976779 0.05531418 0.06562603
0.06613487 0.05446428 0.05543637 0.05121708 0.05309761 0.04277307
0.10968715 0.07820207 0.0767827 0.06629646 0.16126555 0.12621939
0.05119461 0.03338242 0.03414828 0.00957149 0.03263533 0.05339915
0.02484387 0.01161325 0.00200593 0.01138395 0.02554029 0.04895431
0.03807372 0.02062756 0.0154568 0.01590681 0.02791274 0.02735269
0.04096019 0.03589272 0.02912009 0.04779804 0.03241366 0.02944213
0.03430766 0.01269531 0.04131424 0.04561275 0.0444417 0.06222981
0.06027091 0.06683141 0.0583787 0.06367064 0.06087917 0.05638546
0.04805213 0.0325073 0.03921735 0.03834468 0.03973389 0.04760766
0.0400005 0.03318459 0.04373682 0.05061489 0.11348236 0.06625718
0.067204 0.04159379 0.13865781 0.15187544 0.01841801 0.01296431
0.0191946 0. 0.03205788 0.05170709 0.03021151 0.0359363
0.04743361 0.04062575 0.06267166 0.06871426 0.06362879 0.08524656
0.0883559 0.07535374 0.07738322 0.07902771 0.07747477 0.07297075
0.06051964 0.06934726 0.06946731 0.0843156 0.08916569 0.06445265
0.08605701 0.08041549 0.07751596 0.0773887 0.07991475 0.08395034
0.08094996 0.08142078 0.093463 0.09198755 0.10336596 0.09321791
0.07594323 0.08135563 0.07553017 0.04866445 0.02504271 0.05239832
0.0586803 0.05203778 0.12791038 0.09577066 0.09558219 0.09578508
0.17164493 0.21298999 0.03146422 0.02000684 0.03368282 0.02206904
0.0276376 0.07233953 0.04360646 0.03332233 0.04601586 0.05868185
0.08100933 0.08031625 0.09417981 0.08421832 0.06971997 0.0718779
0.05960423 0.06592184 0.07434797 0.07424688 0.05336249 0.06853324
0.07270408 0.08315229 0.09463751 0.05335909 0.0908969 0.09512329
0.08785361 0.08976018 0.08435434 0.08913296 0.08381081 0.08432609
0.10472298 0.0985986 0.0907439 0.09017849 0.08923775 0.1000483
0.0949443 0.09798914 0.08653367 0.08831507 0.09684217 0.07430595
0.16116196 0.11657226 0.1147424 0.1055246 0.16305876 0.19989055
0.09251314 0.11429912 0.11146176 0.08868146 0.09490699 0.11580795
0.12179691 0.10142392 0.10373527 0.10427195 0.10532457 0.10889518
0.1128608 0.10858727 0.11134827 0.15144092 0.13759512 0.12894458
0.13912773 0.13647884 0.12963891 0.13039225 0.13749033 0.14049989
0.14742929 0.10658443 0.1116004 0.13513565 0.12752867 0.12900126
0.1284669 0.13254756 0.1306572 0.12794101 0.1331523 0.14371604
0.13458335 0.14357698 0.1413911 0.15500301 0.14933383 0.15303028
0.13621032 0.14334375 0.14723796 0.14965647 0.22281337 0.17005306
0.18671739 0.18411511 0.18996602 0.31451958 0.15261698 0.14136636
0.14481282 0.14426798 0.12076902 0.13156968 0.1699472 0.13584834
0.12285781 0.12325066 0.11768788 0.14312804 0.12966347 0.12654543
0.14827979 0.14439839 0.12591445 0.14221102 0.12810874 0.14931911
0.15357113 0.14263618 0.15286553 0.17623997 0.17829126 0.16209275
0.12943578 0.1635825 0.16691726 0.16248941 0.17959946 0.18024546
0.17197752 0.17583787 0.17739284 0.16693681 0.11243623 0.13554513
0.15311623 0.16751206 0.15759355 0.15739197 0.13999206 0.14337987
0.18085277 0.17847568 0.26671988 0.2247954 0.21978688 0.20146883
0.21103162 0.3453591 0.22662759 0.20908386 0.23053497 0.22460967
0.21735048 0.21898037 0.25925958 0.21916693 0.21205044 0.2147159
0.22357982 0.19446886 0.24122667 0.25258595 0.23530155 0.23225129
0.2341333 0.23865652 0.2395792 0.24261749 0.24640179 0.22088009
0.25096613 0.2525633 0.24716812 0.2503726 0.21061015 0.25215572
0.23955351 0.23569173 0.23692882 0.23378778 0.2347104 0.23378909
0.23631573 0.23477703 0.21299672 0.24368286 0.24352568 0.24667418
0.24982303 0.24822599 0.25453323 0.2540291 0.27752805 0.27410322
0.27445108 0.35099626 0.3153084 0.3074466 0.31877398 0.41279542
0.3723023 0.2681588 0.28050238 0.23934865 0.2839983 0.24766368
0.2872265 0.26790696 0.26204735 0.17439169 0.2538151 0.25617862
0.25707603 0.25979614 0.25577617 0.26985395 0.26588273 0.24143696
0.26930183 0.25875127 0.24779844 0.23824131 0.25097895 0.2542495
0.2729568 0.27808517 0.22996134 0.27918434 0.27707058 0.27320242
0.27377254 0.27873933 0.2927454 0.2806518 0.28658116 0.25322384
0.24947709 0.26539743 0.26456797 0.27291077 0.29922158 0.2844544
0.28038663 0.2729683 0.2922625 0.28184712 0.28520548 0.37510288
0.34318328 0.32724917 0.31278068 0.42240858 0.42963552 0.29595423
0.307324 0.2976634 0.28231508 0.25331897 0.31515247 0.26604724
0.2599706 0.26265484 0.2503656 0.27110207 0.27458364 0.27708822
0.276291 0.26639533 0.25920528 0.25688434 0.26347655 0.25542635
0.25196058 0.23996127 0.25348955 0.2771018 0.27625567 0.28393883
0.24327934 0.27309048 0.28277338 0.2867338 0.28967685 0.28540558
0.2805786 0.28281105 0.27360332 0.2726066 0.32427615 0.2577905
0.24921316 0.2527899 0.27239174 0.25745118 0.25190902 0.24290574
0.2795834 0.27516508 0.2727751 0.3629216 0.31941646 0.30821562
0.31617934 0.36389583 0.42113793 0.2594359 0.2786746 0.24253035
0.24806243 0.24568498 0.267066 0.30413252 0.26897353 0.24091834
0.24580127 0.24742168 0.29576445 0.29738635 0.25617433 0.2607051
0.26541102 0.25956315 0.26494414 0.27853483 0.28267187 0.2841227
0.2819233 0.296268 0.29833984 0.30373007 0.30070204 0.31147474
0.31756055 0.3170182 0.3122424 0.32684678 0.32724863 0.322115
0.31295848 0.31221402 0.28895038 0.28367442 0.26137316 0.28923357
0.3032781 0.30837065 0.3112409 0.30136555 0.30546248 0.32382834
0.3276466 0.46497464 0.3828706 0.3979993 0.39367008 0.43090093
0.57964635 0.3820684 0.39120817 0.38537866 0.380628 0.32725245
0.34871197 0.38178682 0.3647622 0.33625412 0.34620035 0.36798495
0.37415153 0.34636295 0.32347918 0.37518346 0.34385353 0.3017311
0.3235674 0.33758223 0.35097426 0.3427006 0.36457348 0.37002456
0.39584935 0.39217532 0.39778042 0.39730906 0.41000438 0.41319633
0.41373253 0.4168948 0.41615176 0.41306055 0.41023946 0.4188255
0.41469467 0.40262067 0.41095018 0.420357 0.4411347 0.42617273
0.4197259 0.39035487 0.3885066 0.4145515 0.40718806 0.54886377
0.44413865 0.43839085 0.45436084 0.5045612 0.6314254 0.4119451
0.41329372 0.38737285 0.38495702 0.33678925 0.3691935 0.43968093
0.3803631 0.36547548 0.3596804 0.36043876 0.37673038 0.37449068
0.42373264 0.40112698 0.37705874 0.35835296 0.3640992 0.37732583
0.38723338 0.3764714 0.36331737 0.37724203 0.38594854 0.4035486
0.3938731 0.38519013 0.43583894 0.44315064 0.45545018 0.47120702
0.47178555 0.4560722 0.44470417 0.4526795 0.42386413 0.3900144
0.41063368 0.41430235 0.45591712 0.45053387 0.4734025 0.45310044
0.40982902 0.42201996 0.62515604 0.68869495 0.51969194 0.48238075
0.47657955 0.535686 0.7041838 0.48722327 0.4055487 0.43465245
0.3971895 0.37669533 0.36562502 0.41208124 0.38336515 0.34763825
0.34050214 0.35741037 0.39801157 0.3971548 0.3664527 0.3631217
0.3807991 0.36365432 0.39154446 0.37076157 0.3822567 0.38518518
0.37649006 0.37849855 0.3732537 0.39138973 0.41723073 0.3783326
0.44269907 0.44895148 0.45518208 0.46853483 0.47983527 0.47718787
0.4606849 0.47573364 0.4019934 0.38460928 0.40625906 0.38370568
0.40007448 0.44524848 0.4362569 0.44129777 0.42840743 0.44080877
0.42896044 0.41651177 0.63164556 0.5106875 0.4926597 0.4967116
0.6614512 0.63127136 0.41607153 0.4645145 0.42290032 0.40719926
0.3656633 0.46453035 0.4368037 0.3915404 0.40615582 0.40768647
0.41686785 0.4074298 0.42554843 0.5032058 0.4968593 0.41677952
0.39219868 0.40452433 0.42329156 0.42935717 0.4973601 0.520337
0.54870665 0.5806416 0.6012964 0.5343671 0.5879284 0.61513925
0.61601067 0.6022514 0.6310798 0.640046 0.61407113 0.6006274
0.5697825 0.5441599 0.53212535 0.5163621 0.520661 0.553105
0.5286294 0.48162007 0.4355526 0.4972142 0.48914087 0.4854225
0.7618512 0.6295136 0.6080104 0.5947943 0.7705176 0.80724275
0.5234815 0.53957295 0.50877106 0.4936577 0.4548217 0.5852699
0.5245849 0.4406501 0.44883704 0.47721076 0.48322952 0.4917451
0.55852723 0.5360124 0.48000896 0.47166705 0.49641228 0.50546
0.51512635 0.52145946 0.51673305 0.5225092 0.5320723 0.5602486
0.55347633 0.52746475 0.56462324 0.58124757 0.5756283 0.57236886
0.5835146 0.5745715 0.5600463 0.5416546 0.55585027 0.48987508
0.49237514 0.50569725 0.49848998 0.54686713 0.5002457 0.5083971
0.44955313 0.4764521 0.5052068 0.53641176 0.72663784 0.6194565
0.60785604 0.6094575 0.7373266 0.83010805 0.58855665 0.56729686
0.5457535 0.4969293 0.4473629 0.49508893 0.5869677 0.57742465
0.45357692 0.46955323 0.5016581 0.4512154 0.45280957 0.43442798
0.47744536 0.62240505 0.5364413 0.50953686 0.49155688 0.5515157
0.55041194 0.5250572 0.5397192 0.5581243 0.6151464 0.59002066
0.6108477 0.60503125 0.62597597 0.61851203 0.6333308 0.6291685
0.60309803 0.5466509 0.5832646 0.517396 0.55823433 0.55684745
0.57499874 0.6637217 0.65186214 0.6326506 0.61108565 0.60191894
0.6195426 0.5910344 0.80722487 0.66512215 0.6559496 0.6697364
0.7436224 1. 0.6921803 0.6377411 0.59824586 0.54307234
0.5016414 0.5689379 0.69034994 0.6618624 0.5531596 0.58237886
0.6278132 0.6240814 0.65015244 0.73547316 0.7202023 0.6216053
0.6118895 0.63003385 0.6237917 0.66039157 0.6744511 0.67192984
0.69771504 0.70374286 0.7356286 0.74151945 0.7086481 0.72226715]
5.データの整形
スケーリングし、入力データ・正解ラベルにしたデータをLSTMに流し込める形に変形していきます。
行数×変数数×カラム数の3次元の行列に変換します。
行数、変数数は.shapeメソッドにて出していきます。
カラム数は特徴量の列数なので、今回は1となります。
取得した数でreshapeにより3次元の行列に変換していきます。
# 3次元のnumpy.ndarrayに変換
train_X = train_X.reshape(train_X.shape[0],train_X.shape[1],1)
test_X = test_X.reshape(test_X.shape[0],test_X.shape[1],1)
6.LSTMネットワークの構築と訓練
ここまでで準備が完了したので、モデルの構築に移ります。
model = keras.Sequential()
model.add(layers.LSTM(128, input_shape=(look_back, 1),return_sequences=True))
model.add(layers.LSTM(32))
model.add(layers.Dense(1))
# モデルをコンパイル
model.compile(loss='mean_squared_error', optimizer='adam')
# 訓練
model.fit(train_X, train_Y, epochs=30, batch_size=3, verbose=2)
>>> 出力結果
Epoch 1/30
282/282 - 5s - loss: 0.0088 - 5s/epoch - 17ms/step
Epoch 2/30
282/282 - 2s - loss: 0.0031 - 2s/epoch - 6ms/step
Epoch 3/30
282/282 - 2s - loss: 0.0030 - 2s/epoch - 6ms/step
Epoch 4/30
282/282 - 2s - loss: 0.0029 - 2s/epoch - 7ms/step
Epoch 5/30
282/282 - 2s - loss: 0.0029 - 2s/epoch - 8ms/step
Epoch 6/30
282/282 - 2s - loss: 0.0028 - 2s/epoch - 8ms/step
Epoch 7/30
282/282 - 1s - loss: 0.0027 - 1s/epoch - 5ms/step
Epoch 8/30
282/282 - 2s - loss: 0.0026 - 2s/epoch - 6ms/step
Epoch 9/30
282/282 - 2s - loss: 0.0025 - 2s/epoch - 5ms/step
Epoch 10/30
282/282 - 1s - loss: 0.0026 - 1s/epoch - 5ms/step
Epoch 11/30
282/282 - 2s - loss: 0.0022 - 2s/epoch - 5ms/step
Epoch 12/30
282/282 - 2s - loss: 0.0022 - 2s/epoch - 5ms/step
Epoch 13/30
282/282 - 2s - loss: 0.0023 - 2s/epoch - 7ms/step
Epoch 14/30
282/282 - 2s - loss: 0.0024 - 2s/epoch - 8ms/step
Epoch 15/30
282/282 - 2s - loss: 0.0022 - 2s/epoch - 8ms/step
Epoch 16/30
282/282 - 1s - loss: 0.0023 - 1s/epoch - 5ms/step
Epoch 17/30
282/282 - 2s - loss: 0.0022 - 2s/epoch - 5ms/step
Epoch 18/30
282/282 - 2s - loss: 0.0022 - 2s/epoch - 5ms/step
Epoch 19/30
282/282 - 1s - loss: 0.0021 - 1s/epoch - 5ms/step
Epoch 20/30
282/282 - 2s - loss: 0.0022 - 2s/epoch - 6ms/step
Epoch 21/30
282/282 - 2s - loss: 0.0022 - 2s/epoch - 5ms/step
Epoch 22/30
282/282 - 2s - loss: 0.0021 - 2s/epoch - 7ms/step
Epoch 23/30
282/282 - 2s - loss: 0.0023 - 2s/epoch - 8ms/step
Epoch 24/30
282/282 - 2s - loss: 0.0022 - 2s/epoch - 8ms/step
Epoch 25/30
282/282 - 1s - loss: 0.0021 - 1s/epoch - 5ms/step
Epoch 26/30
282/282 - 2s - loss: 0.0020 - 2s/epoch - 6ms/step
Epoch 27/30
282/282 - 2s - loss: 0.0023 - 2s/epoch - 5ms/step
Epoch 28/30
282/282 - 2s - loss: 0.0021 - 2s/epoch - 5ms/step
Epoch 29/30
282/282 - 2s - loss: 0.0020 - 2s/epoch - 5ms/step
Epoch 30/30
282/282 - 2s - loss: 0.0021 - 2s/epoch - 5ms/step
<keras.src.callbacks.History at 0x7f30aabfb7f0>
7.データの予測と評価
6で作成したモデルで予測し、その後精度を測っていきます。
モデルに入れる関係で学習データでスケールをしているので、予測後はinverse_transform()を用いて元に戻していく作業も発生しています。
予測精度はRMSE(平均二乗誤差)を用います。値が小さければ小さいほどこのモデルは優れている、と言えます。
# 予測データの作成
train_predict = model.predict(train_X)
test_predict = model.predict(test_X)
# スケールしたデータを元に戻す
train_predict = scaler_train.inverse_transform(train_predict)
train_Y = scaler_train.inverse_transform([train_Y])
test_predict = scaler_train.inverse_transform(test_predict)
test_Y = scaler_train.inverse_transform([test_Y])
# 予測精度の計算
train_score = math.sqrt(mean_squared_error(train_Y[0], train_predict[:, 0]))
print('Train Score: %.2f RMSE' % (train_score))
test_score = math.sqrt(mean_squared_error(test_Y[0], test_predict[:, 0]))
print('Test Score: %.2f RMSE' % (test_score))
>>> 出力結果
27/27 [==============================] - 1s 7ms/step
7/7 [==============================] - 0s 4ms/step
Train Score: 3.54 RMSE
Test Score: 6.62 RMSE
※実際には6と7、そして次の8をいったり来たりして、層の数やノードユニット数、epochやbatch_sizeといった各種パラメータの調整を行い、このRMSEが最も小さくなった値を探る作業をひたすら行っていました。
今回は前回整形したデータセットをほぼそのまま流用したこともあり、この点にとても時間を費やしました。
このパラメータのチューニングに関しては、いくつかのパターンから最適解を設定する試みも今後してみたいです。
8.予測結果の可視化
7で予測した内容を可視化していきます。
比較のため最初のデータセットと並べた可視化を行い、視覚的に精度を確認していきます。
# 訓練データから予測したデータの整形
train_predict_plot = np.empty_like(dataset)
train_predict_plot[:, :] = np.nan
train_predict_plot[look_back:len(train_predict)+look_back, :] = train_predict
# 検証データから予測したデータの整形
# 既存の配列`dataset`と同じ大きさ(行数・列数)、データ型で値を0に初期化したプロット用の空の配列を作成
test_predict_plot = np.empty_like(dataset)
# 空の配列のすべての値を欠損値`nan`にする
test_predict_plot[:, :] = np.nan
# 訓練データの予測値と位置を合わせる
test_predict_plot[len(train_predict)+(look_back*2):len(dataset), :] = test_predict
# データのプロット
plt.title("broadwaymusical_average_prices")
plt.xlabel("date")
plt.ylabel("AveragePrices")
# 読み込んだままのデータをプロット
plt.plot(dataset, label='dataset')
# 訓練データから予測した値をプロット
plt.plot(train_predict_plot, label='train_predict')
# 検証データから予測した値をプロット
plt.plot(test_predict_plot, label='test_predict')
plt.legend(loc='best')
plt.show()
全体として精度良く予測ができているかなと思いますが、このままだとx軸がインデックスの値になってしまっており若干わかりずらいので、datasetを元のmusical_avg_dataを使う形でプロットし直してみます。
# 週ごとの日付リストを作成
weekly=pd.date_range("1996-04-14", periods=1062, freq="W")
#train_predict_plotをDataFrame形式に変換→新たにWeekly列を作成・インデックス化
train_predict_plot_df=pd.DataFrame(train_predict_plot)
train_predict_plot_df = train_predict_plot_df.rename(columns={0: 'Average Prices'})
train_predict_plot_df['Weekly']=weekly
train_predict_plot_df=train_predict_plot_df.set_index('Weekly')
#test_predict_plotをDataFrame形式に変換→新たにWeekly列を作成・インデックス化
test_predict_plot_df=pd.DataFrame(test_predict_plot)
test_predict_plot_df = test_predict_plot_df.rename(columns={0: 'Average Prices'})
test_predict_plot_df['Weekly']=weekly
test_predict_plot_df=test_predict_plot_df.set_index('Weekly')
plt.title("broadway_musical_average_prices")
plt.xlabel("date")
plt.ylabel("AveragePrices")
# 元データ(musical_avg_data)をプロット
plt.plot(musical_avg_data, label='dataset')
# 訓練データ→train_predict_plot_dfをplot
plt.plot(train_predict_plot_df, label='train_predict')
# 検証データ→test_predict_plot_dfをplot
plt.plot(test_predict_plot_df, label='test_predict')
plt.legend(loc='best')
plt.show()
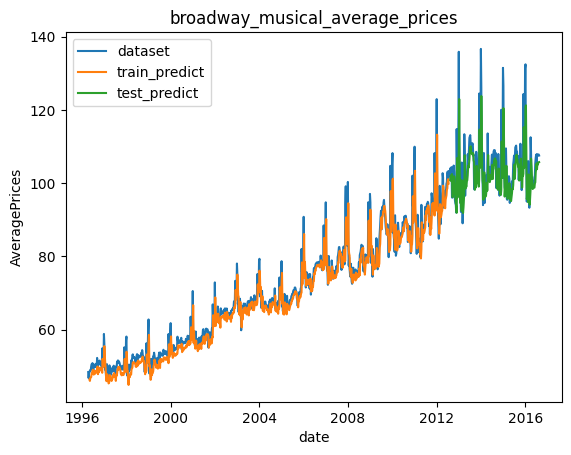
日付をx軸に持ってくることができました。
訓練データと検証データ、いずれもそのままでは使えないので、日付データ入りのDataFrameに変換する形でまとめてみましたが、なにか他にいい方法があれば教えていただけると嬉しいです。
上に振れている部分はほぼ必ず予測が下回っているのが特徴かもしれません。
Figure, ax = plt.subplots()
ax.plot(musical_avg_data,label='dataset')
ax.plot(train_predict_plot_df, label='train_predict')
ax.plot(test_predict_plot_df,label='test_predict')
span=pd.to_datetime(["2011-10-23", "2016-08-14"])
ax.set_xlim(span)
plt.legend(loc='lower right')
# x軸を見やすくするための調整
labels = ax.get_xticklabels()
plt.setp(labels, rotation=45, fontsize=10);
plt.show()
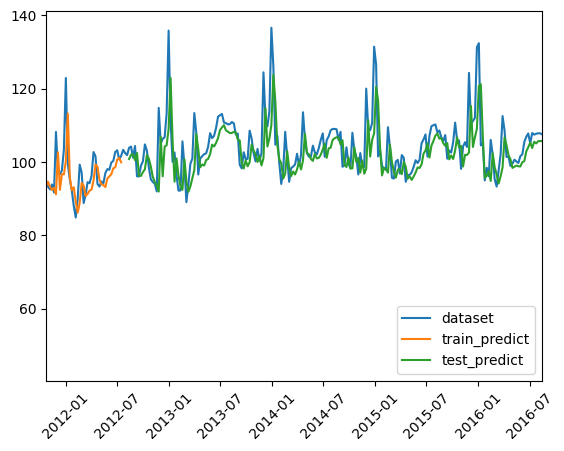
2011-10-23以降の部分を拡大したものです。
このあたりの上に抜けているところ(120ドル以上)が特に予測と元データのギャップが大きくなっているので、年末の平均単価が高いタイミングの予測はこのモデルだと少し苦手と考えると良いかもしれないと思います。
また、年ごとor周期ごとで特に繁忙期に過去よりも平均値を大きく底上げる要素が何かあるのでは…と推測されます。ここの相関が見つかれば、より精度の高いモデルを作ることができるかもしれません。
※参考:元データ=120ドルを超えている週と予測の比較(日曜締め)
- この表によれば、2011年末以降、基本的に年末(および年末を含む年始週)+サンクスギビングデー(11月第4木曜日)が含まれる週のみが120ドルを超えています。
- 一方で予測結果を見ると、8/11件=約72%が20ドル以上の誤差が生まれている状況

※出力時のコード
# 訓練データおよび検証データ(プロット用)を結合
train_predict_plot_df_index=train_predict_plot_df.reset_index()
test_predict_plot_df_index=test_predict_plot_df.reset_index()
all_predict_df=pd.merge(train_predict_plot_df_index,test_predict_plot_df_index, on = 'Weekly', how='outer')
# NaNを0に置き換え
all_predict_df=all_predict_df.fillna(0)
# 'Predict'列を作成し、train、testいずれかデータのある方を格納
all_predict_df['Predct']=np.where(all_predict_df['Average Prices_x']>all_predict_df['Average Prices_y'], all_predict_df['Average Prices_x'], all_predict_df['Average Prices_y'])
# 不要になった列の消去
drop_cols=['Average Prices_x','Average Prices_y']
all_predict_df=all_predict_df.drop(drop_cols,axis=1)
# 元データと予測データのDataFrameを結合
musical_avg_data_check=musical_avg_data.reset_index()
musical_avg_data_check=musical_avg_data_check.rename(columns={'Date.Full':'Weekly'})
musical_avg_data_check=pd.merge(musical_avg_data_check,all_predict_df,on='Weekly',how='outer')
# 実績と予測の誤差を'GAP'列に格納
musical_avg_data_check['GAP']=musical_avg_data_check['Predct']-musical_avg_data_check['AveragePrice']
musical_avg_data_check=musical_avg_data_check.set_index('Weekly')
# 実績120ドル以上の週を出力
musical_avg_data_over120=musical_avg_data_check[musical_avg_data_check['AveragePrice'] > 120]
musical_avg_data_over120=musical_avg_data_over120.reset_index()
musical_avg_data_over120
+α:季節変動周期をlook_backの値に反映してみる
一旦今回の目標(モデルを作り精度を測る)としてはクリアなのですが、今回create_dataset()関数のlook_downが「基準点を元に何期前までのデータを遡るか」を決めるものなので、前回確認をした変動周期を当てはめてみたらどのような結果になるか、見ていこうと思います。
- 季節変動周期=2年≒102週
- 「基準点を元に何期前までのデータを遡るか」なので
look_back=101に設定してモデリングを行う
# 入力データが何週分のデータを取るかを定義
look_back = 101
# 作成した関数`create_dataset`を用いて、入力データ・正解ラベルを作成
train_X, train_Y = create_dataset(train, look_back)
test_X, test_Y = create_dataset(test, look_back)
# 3次元のnumpy.ndarrayに変換
train_X = train_X.reshape(train_X.shape[0],train_X.shape[1],1)
test_X = test_X.reshape(test_X.shape[0],test_X.shape[1],1)
# LSTMモデルを作成
model = keras.Sequential()
model.add(layers.LSTM(128, input_shape=(look_back, 1),return_sequences=True))
model.add(layers.LSTM(32))
model.add(layers.Dense(1))
# モデルをコンパイル
model.compile(loss='mean_squared_error', optimizer='adam')
# 訓練
model.fit(train_X, train_Y, epochs=30, batch_size=3, verbose=2)
モデルの学習過程
Epoch 1/30
250/250 - 25s - loss: 0.0051 - 25s/epoch - 99ms/step
Epoch 2/30
250/250 - 21s - loss: 0.0037 - 21s/epoch - 85ms/step
Epoch 3/30
250/250 - 22s - loss: 0.0034 - 22s/epoch - 87ms/step
Epoch 4/30
250/250 - 27s - loss: 0.0028 - 27s/epoch - 109ms/step
Epoch 5/30
250/250 - 20s - loss: 0.0027 - 20s/epoch - 80ms/step
Epoch 6/30
250/250 - 21s - loss: 0.0029 - 21s/epoch - 85ms/step
Epoch 7/30
250/250 - 22s - loss: 0.0028 - 22s/epoch - 86ms/step
Epoch 8/30
250/250 - 21s - loss: 0.0024 - 21s/epoch - 84ms/step
Epoch 9/30
250/250 - 20s - loss: 0.0024 - 20s/epoch - 79ms/step
Epoch 10/30
250/250 - 21s - loss: 0.0026 - 21s/epoch - 82ms/step
Epoch 11/30
250/250 - 21s - loss: 0.0026 - 21s/epoch - 82ms/step
Epoch 12/30
250/250 - 20s - loss: 0.0027 - 20s/epoch - 82ms/step
Epoch 13/30
250/250 - 20s - loss: 0.0023 - 20s/epoch - 80ms/step
Epoch 14/30
250/250 - 20s - loss: 0.0024 - 20s/epoch - 81ms/step
Epoch 15/30
250/250 - 22s - loss: 0.0024 - 22s/epoch - 88ms/step
Epoch 16/30
250/250 - 21s - loss: 0.0026 - 21s/epoch - 84ms/step
Epoch 17/30
250/250 - 20s - loss: 0.0023 - 20s/epoch - 79ms/step
Epoch 18/30
250/250 - 21s - loss: 0.0022 - 21s/epoch - 83ms/step
Epoch 19/30
250/250 - 20s - loss: 0.0023 - 20s/epoch - 81ms/step
Epoch 20/30
250/250 - 20s - loss: 0.0023 - 20s/epoch - 81ms/step
Epoch 21/30
250/250 - 21s - loss: 0.0025 - 21s/epoch - 82ms/step
Epoch 22/30
250/250 - 21s - loss: 0.0023 - 21s/epoch - 83ms/step
Epoch 23/30
250/250 - 22s - loss: 0.0023 - 22s/epoch - 88ms/step
Epoch 24/30
250/250 - 21s - loss: 0.0023 - 21s/epoch - 83ms/step
Epoch 25/30
250/250 - 20s - loss: 0.0022 - 20s/epoch - 81ms/step
Epoch 26/30
250/250 - 20s - loss: 0.0022 - 20s/epoch - 80ms/step
Epoch 27/30
250/250 - 21s - loss: 0.0022 - 21s/epoch - 82ms/step
Epoch 28/30
250/250 - 19s - loss: 0.0022 - 19s/epoch - 77ms/step
Epoch 29/30
250/250 - 21s - loss: 0.0022 - 21s/epoch - 84ms/step
Epoch 30/30
250/250 - 20s - loss: 0.0023 - 20s/epoch - 78ms/step
<keras.src.callbacks.History at 0x789439e11a20>
# 予測データの作成
train_predict = model.predict(train_X)
test_predict = model.predict(test_X)
# スケールしたデータを元に戻す
train_predict = scaler_train.inverse_transform(train_predict)
train_Y = scaler_train.inverse_transform([train_Y])
test_predict = scaler_train.inverse_transform(test_predict)
test_Y = scaler_train.inverse_transform([test_Y])
# 予測精度の計算
train_score = math.sqrt(mean_squared_error(train_Y[0], train_predict[:, 0]))
print('Train Score: %.2f RMSE' % (train_score))
test_score = math.sqrt(mean_squared_error(test_Y[0], test_predict[:, 0]))
print('Test Score: %.2f RMSE' % (test_score))
>>>出力結果
24/24 [==============================] - 2s 57ms/step
4/4 [==============================] - 0s 49ms/step
Train Score: 3.39 RMSE
Test Score: 6.43 RMSE
train_predict_plot = np.empty_like(dataset)
train_predict_plot[:, :] = np.nan
train_predict_plot[look_back:len(train_predict)+look_back, :] = train_predict
test_predict_plot = np.empty_like(dataset)
test_predict_plot[:, :] = np.nan
test_predict_plot[len(train_predict)+(look_back*2):len(dataset), :] = test_predict
train_predict_plot_df=pd.DataFrame(train_predict_plot)
train_predict_plot_df = train_predict_plot_df.rename(columns={0: 'Average Prices'})
train_predict_plot_df['Weekly']=weekly
train_predict_plot_df=train_predict_plot_df.set_index('Weekly')
test_predict_plot_df=pd.DataFrame(test_predict_plot)
test_predict_plot_df = test_predict_plot_df.rename(columns={0: 'Average Prices'})
test_predict_plot_df['Weekly']=weekly
test_predict_plot_df=test_predict_plot_df.set_index('Weekly')
plt.title("broadway_musical_average_prices")
plt.xlabel("date")
plt.ylabel("AveragePrices")
plt.plot(musical_avg_data, label='dataset')
plt.plot(train_predict_plot_df, label='train_predict')
plt.plot(test_predict_plot_df, label='test_predict')
plt.legend(loc='best')
plt.show()
Figure_2, ax_2 = plt.subplots()
ax_2.plot(musical_avg_data,label='dataset')
#ax_2.plot(train_predict_plot_df, label='train_predict')
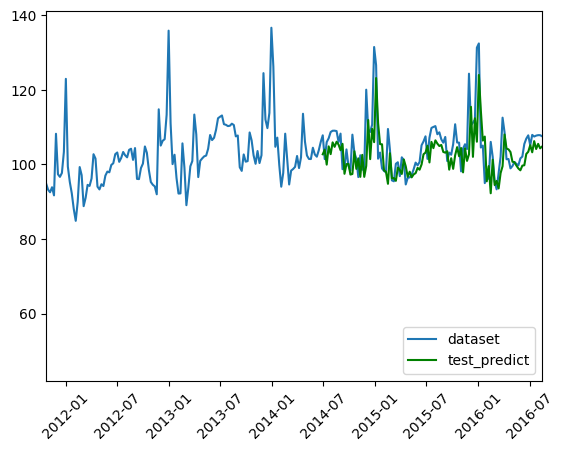
ax_2.plot(test_predict_plot_df,label='test_predict',color="g")
span=pd.to_datetime(["2011-10-23", "2016-08-14"])
ax_2.set_xlim(span)
plt.legend(loc='lower right')
labels = ax_2.get_xticklabels()
plt.setp(labels, rotation=45, fontsize=10);
plt.show()
look_bacK=3の場合と同じ流れで可視化まで行いました。
周期をかなり大きくしているため、予測結果のないブランク箇所がかなり大きくなっています。
精度については下記表でまとめました。
| look back= | Train Score | Test Score |
|---|---|---|
| 3 | 3.54 | 6.62 |
| 101 | 3.39 | 6.43 |
look_back=3と比較して、訓練データ・テストデータともに微減していることは確認できましたが、大幅な精度改善には至っていないことが伺えます。やはりこれよりも精度をあげていくには、繁忙期における別の特徴量との相関関係を探るなど、別の方向からのアプローチが必要だと思われます。
終わりに
今回は前回の反省をもとに、ブロードウェイミュージカルの平均単価値上げ状況の予測モデルについて、LSTMを用いて考えてみました。
SARIMAモデルではできなかった週単位の予測モデルについて、LSTMを用いることで実現をすることができました。
一方、特に繁忙期週の予測精度が低い状況のため、別の特徴量との相関関係を考えたり、層の数やパラメータの調整によってより高い精度のモデルを目指していけたらと思っております。