LoginSignup
14
8

More than 5 years have passed since last update.

文字列アルゴリズムAdvent Calendar 2017Day 15
@hdbn

アルファベットサイズに依存しないリアルタイム KMP 法

Last updated at Posted at 2017-12-13

この記事は、「文字列アルゴリズム Advent Calendar 2017」15日目の記事です。

どうも、文字列大好き @hdbn です。

この記事では文字列照合アルゴリズムとして有名な Knuth-Morris-Pratt1アルゴリズム （以下 KMP 法）の(アルファベットサイズに依存しない)「リアルタイム」版を解説します。KMP 法をある程度知っていたほうが読み易いかもしれません。また、決定性有限オートマトンと非決定性有限オートマトンについての知識を前提としています。

KMP 法は(文字列マニアではない)一般人向けにも数多くの解説記事があります。一方で「KMP 法はリアルタイムとなるように変更できる」という記述を多少見たことがある2ものの、実際に(アルファベットサイズに依存しない)リアルタイム版をどう実現すれば良いのかを解説したものを見たことがなかったのでこのテーマを選んでみました。

文字列照合問題と「リアルタイム」

「文字列照合問題」は一般には、「入力として長さ $n$ のテキスト文字列 $T = T[0..n-1]$ と長さ $m$ のパターン文字列 $P = P[0..m-1]$ が与えられたときに、$T$ 中の $P$ のすべての出現、すなわち $T[i-m+1..i] = P$ となるようなすべての $m-1 \leq i \leq n-1$ を出力する問題」です3が、今回は次のような「オンライン」な設定を考えます。

この設定では、アルゴリズムは最初にパターンを与えられた後、テキストを１文字ずつ与えられ、テキスト１文字与えられる毎に、これまで与えられたテキスト文字列の末尾にパターンが出現するか否かを答えなければなりません。素朴なアルゴリズムは以下のように実装できます。

オンライン文字列照合問題に対する素朴なアルゴリズム
class Naive {
  std::string pat;      // パターン
  std::deque<char> txt; // テキストのための FIFO バッファ: O(1) push/pop/access
 public:
  Naive(const std::string& pattern) : pat(pattern) {} // 前処理なし
  bool next(char c) {
    txt.push_back(c);
    if (txt.size() > pat.size()) txt.pop_front(); // パターン長と同じ分だけテキストを保持
    if (txt.size() < pat.size()) return false;    // テキストがまだ足りない場合
    for (int i = 0; i < pat.size(); i++) {        // |txt| = |pat|
      if (pat[i] != txt[i]) return false;
    }
    return true;
  }
};

上の素朴なアルゴリズムは、次のテキスト１文字を与えるメソッド bool next(char c) の計算に最悪の場合 $\Theta(m)$ 時間かかるため、合計 $n$ 文字与えられたとすると $O(nm)$ 時間アルゴリズムではありますが、線形時間 ($O(n+m)$ 時間)アルゴリズムではありません。

KMP 法は、$O(m+n)$ 時間アルゴリズムであり、このオンラインな問題設定でも(長さ $m$ のパターンに対して $O(m)$ の前処理をした後で) テキストを１文字ずつ合計 $n$ 文字与えられたときに、各文字に対する答えを全体で $O(n)$ 時間で答えてくれるアルゴリズム、と見ることができます。これは、アルゴリズム全体を通して平均するとテキスト１文字あたり定数 ($O(1)$) 時間で答えてくれることを意味しますが、特定のテキスト１文字に対してはやはり答えを返すまで最悪 $\Theta(m)$ 時間4かかることがあります。つまり１文字の追加入力に対して答えが返ってくるまでに待たされる時間の幅が結構あり得る、ということになります。

これに対して、「リアルタイム」なアルゴリズムとは、テキストが１文字与えられる度に、どんな場合でも定数時間で答えてくれるアルゴリズムのことです。言い換えれば、どんな文字列であっても、１文字の追加テキストに対して、決まった長さの時間を待てば必ず答えが返ってくることが保証されたアルゴリズムです。つまり KMP 法は線形時間アルゴリズムではありますが、そのままではリアルタイムなアルゴリズムではありません。

以下では KMP 法を復習した上で、これをリアルタイムに動作させるにはどうすれば良いかを解説します。

KMP 法のアイディア

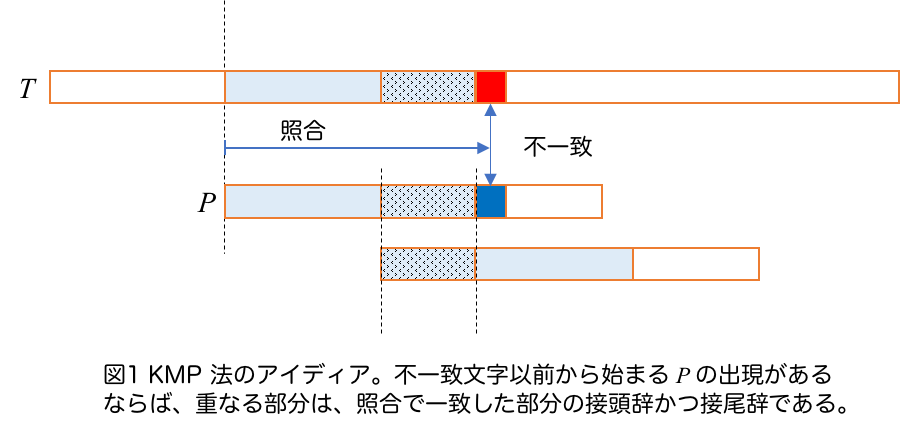
まずは、オンラインではない、普通の問題設定での KMP 法のアイディアを説明します。KMP 法は、パターンをテキストのある位置（最初はテキストの先頭に）にあてがい、パターンとテキストの対応する文字を左から１文字ずつ比較していきます。パターンの最後まで照合が成功するか（その際はパターンの出現を出力）、もしくは途中で不一致があった場合、パターンとテキストが一致した部分（パターンの接頭辞）の情報を元に、次にパターンが出現することができる直近のテキスト位置までパターンをあてがう位置をずらし、これをあてがうテキスト位置がテキストの終わりに来るまで繰り返します。

あてがう位置をずらす際、出現を漏らさずにどのくらいずらして良いのかを考えましょう。下の図から分かる通り、テキストと一致したパターンの接頭辞において、(真の)接尾辞かつ接頭辞である（以下、ボーダーと呼ぶ）最長のものが重なるまでずらしてよいことがわかります。

kmp-idea.png

また、ずらした後、ボーダーが重なる部分についてパターンとテキストは一致することが保証されているので、再度比較する必要がなく、比較は不一致となったテキスト位置から開始して良いことになります。このようなアルゴリズムにおいて、比較回数を結果毎に集計すると、文字が一致する回数は高々 $n$ 回、また、文字が不一致となるとパターンをあてがうテキスト位置が増えるのでこれも高々 $n$ 回(正確には $n-m+1$回)であり、全体で総比較回数が高々 $2n$ 回と言えます。以上のことから、パターンの各接頭辞の最長ボーダーが分かっていればアルゴリズムは $O(n)$ 時間で動作することが分かります。

KMP 法の前処理はまさにこの最長ボーダーの計算で、パターン $P$ の各接頭辞 $P[0..i-1]~(1 \leq i \leq m)$ について、その最長ボーダーの長さ $B[i]$ を計算しておきます。あるテキスト位置で照合の結果、$P$ の先頭 $i$ 文字（つまり $P[0..i-1]$）がテキストと一致したとき、位置を $i-B[i]$ ずらしてもよい、ということになります。また、$B[0] = -1$ としておけば、1文字も一致しない場合にも位置を $0 - (-1) = 1$ つずらすことになります。

ボーダー配列 $B$ は以下のように線形($O(m)$)時間で計算することができます。(詳細は省略)

ボーダーの計算
void makeBorder(const std::string & pat, std::vector<int> & brd){
    int  i = -1, j = 0, m = pat.size()+1;
    brd.resize(m);
    brd[0] = -1;
    while(j < m){
        while(i >= 0 && pat[i] != pat[j]) i = brd[i];
        brd[++j] = ++i;
    }
}

KMP 法とオートマトン

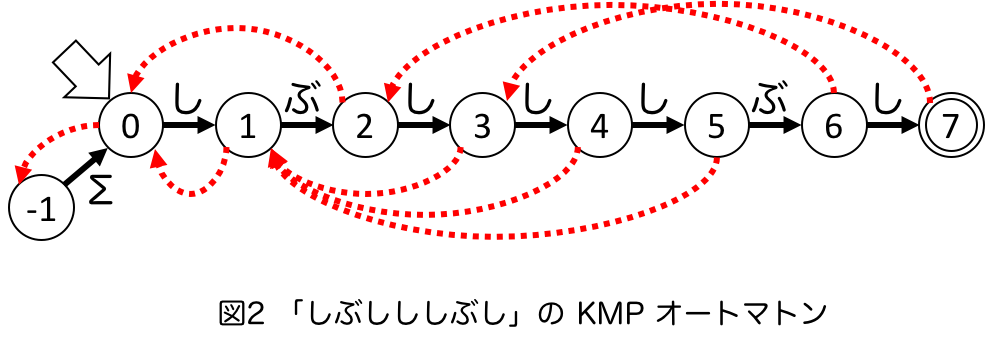
ボーダー配列が計算できれば、照合のアルゴリズムは上の説明から実装できると思いますが、ここではオンラインな設定に対応するために少し視点を変えて、KMP 法を 非決定性有限状態オートマトン（以下NFA）上の動作として考えることにします。例えば、$P =$「しぶしししぶし」という文字列を考えると、そのボーダー配列は $B[0..7] = (-1,0,0,1,1,1,2,3)$ です。このボーダー配列に対して、下の図のような NFA を考えます。赤色の点線矢印と、ボーダー配列の値が対応しています。ここで、各状態で黒色の実線矢印は普通の遷移関数で、パターンの各位置に対応する状態から、対応する文字で次の位置に対応する状態まで遷移できます。ただし、状態 -1 からは任意の文字（Σと表記）で遷移できることとしています。赤色の点線矢印は ε 遷移で、KMP オートマトンでは failure link と呼ばれます。黒色の実線矢印での遷移は、対応する位置のテキストとパターンの文字が一致したということ、failure link による遷移は不一致が生じたためにパターンをあてがう位置をずらすこととそれぞれ解釈することができます。

kmp-shibushi.png

このオートマトンは $P$ を接尾辞に持つ文字列全体を受理します。ε遷移のある NFA なので、開始状態からはじめ、テキストの各文字を順番にこのオートマトンに入力していき、到達可能な状態の中に受理状態があるならば受理(=その位置で終わるパターンの出現があった)、ということです。通常、NFA の動作を考える場合には到達可能な状態の集合を考えないといけないのですが、KMP オートマトンの場合はその性質から（到達可能な状態の集合において状態に対応する文字列は同集合中のより長い文字列のボーダーになっている、受理状態は最右の状態のみ等）、到達可能な状態のうち、一番受理状態に近いものだけを考えれば受理状態に到達可能であったかどうかを正しく判断できます。つまり、開始状態から始め、現在の状態からテキストの文字で遷移できれば遷移し、できない場合は failure link を辿った上でもう一度遷移できるかを試み、そのテキスト文字で遷移できるまで繰り返す、といった動作で良いことになります。（$B[0]=-1$ に対応する状態からは任意の文字で遷移できるため、最後には必ずテキスト文字で遷移できます）

このオートマトン上の動作は、以下のように実装することができます。

KMPオートマトン
class KMPAutomaton {
  int j;                  // オートマトン上の現状態
  const std::string pat;  // パターン
  std::vector<int> brd;   // パターンのボーダー配列 (failure link)
 public:
  KMPAutomaton(const std::string& pattern) : pat(pattern) {
    makeBorder(pat, brd); // オートマトン (failure link) の構築
    j = 0;                // 現状態の初期化
  }
  bool next(char c) {
    while (j >= 0 && pat[j] != c) j = brd[j]; // 文字が一致しない間は failure link を辿る
    j++;                                      // (一致するので) 黒色矢印で遷移
    if (j == pat.size()) {                    // 受理状態に到達したので true
      j = brd[j]; return true;
    }
    return false;                             // 受理状態ではないので false
  }
};

KMP 法のリアルタイム版

KMP オートマトンの嬉しい点としては、元のパターンのアルファベットサイズ(使われている文字の種類数)に関わらず、各状態から黒色と赤色の高々2つの遷移だけで表現できている点です。しかし、上で述べた様に NFA の動作としては、ある状態から入力テキスト文字で遷移できない場合に、到達可能状態を更新するために failure link を辿ってから再度その文字で遷移できるかを試す必要があり、その入力テキスト文字に対する到達可能状態（の最大値）を得るために、最悪 $\Theta(m)$ 回 failure link をたどる必要があります。これが、KMP 法がそのままではリアルタイムではない所以です。この部分を、定数時間に抑えることは可能でしょうか？

巷でよく見る KMP 法のリアルタイム版の解説は、KMP オートマトンを決定性有限オートマトンに変換するものです (例えば英語版 Wikipedia の KMP)。これは、要はオートマトンの各状態とアルファベットの各文字毎に、その文字が次の１文字だった時に最終的にどこに遷移するかを予め計算しておく、ということです。が、この方法はアルファベットサイズを $\sigma$ とすると明らかに $\Theta(\sigma m)$ 領域かかってしまうため、(日本語とか)アルファベットサイズが大きい場合によくありません。

アルファベットサイズが大きい時でもオートマトンのサイズを大きくせずにリアルタイムな動作はどう実現すれば良いでしょうか？答えは実はとても簡単で、以下のように実装できます。

リアルタイムKMP
class KMPAutomatonRT {
  int j;                  // オートマトン上の現状態
  const std::string pat;  // パターン
  std::vector<int> brd;   // パターンのボーダー配列 (failure link)
  std::queue<char> txt;   // テキストのための FIFO バッファ O(1) push/pop

 public:
  KMPAutomatonRT(const std::string& pattern) : pat(pattern) {
    makeBorder(pat, brd); // オートマトン (failure link) の構築
    j = 0;                // 現状態の初期化
  }
  bool next(char c) {
    txt.push(c);
    if (j >= 0 && pat[j] != txt.front()) j = brd[j];   // 文字が一致しないので failure link を辿る
    else { txt.pop(); j++; }                           // 文字が一致したので黒矢印で遷移
    if (!txt.empty()) {                                // 未処理文字がある場合にはもう一度だけ遷移を試みる
      if (j >= 0 && pat[j] != txt.front()) j = brd[j];  // 文字が一致しないので failure link を辿る
      else { txt.pop(); j++; }                          // 文字が一致したので黒矢印で遷移
    }
    if (j == pat.size()) {                             // 受理状態に到達したので true
      j = brd[j]; return true;                         // このとき、バッファ txt は空
    }
    return false;                                      // 受理状態ではないので false
  }
};

普通の KMP 法との違いは、与えられたテキスト１文字での遷移が成功するまでループする while 文の代わりに、未処理(厳密には、処理中か未処理)のテキスト文字を保持するためのバッファを導入し、高々2回の遷移を試みた上で、答えを返すようにした点です。アルゴリズムが正しければ、ループが無いので bool next(char c) がリアルタイムの要件を満たしていることと、必要な領域が $O(m)$ で収まっていることはわかると思いますが、なぜこれで正しいのでしょうか？

正しさの直感的な説明

ある文字に関する動作において、現状態から受理状態までの距離が $2$ 以上あるならば、その文字に関して (元の KMP 法の意味で) 完全に処理が終わらなくとも、結果が false になることが保証できます。failure link を辿ると未処理の文字がバッファに溜まってるいきますが、この距離が増えます。これらの未処理文字を「結果が false でなければならないことが保証されている」間に、false と出力しつつちょっとずつ処理することで、true となり得る文字が入力されるまでには処理を終えている、といった感じです。

正しさの詳しい説明

アルゴリズムは、テキストが１文字与えられる毎に、その文字をバッファの末尾に追加した上で、「バッファの先頭にあるテキスト文字に関して遷移を試み、遷移できるなら遷移してその文字をバッファから削除し、できなければ failure link を辿る」という操作を(最大)２回繰り返します。ここで、バッファに溜まった文字数を $k$、現状態 $j$ から受理状態までの距離を $d = m - j$ とすると bool next(char c) が呼び出される前後での不変条件として、

  • 『$d \geq 2k$』

が成り立つことを示します。アルゴリズムの開始時には $k = 0$ であるため成り立ちます。bool next(char c) の呼び出し時に $d \geq 2k$ が成り立ち、return 時の $d,k$ の値をそれぞれ $d',k'$ としたときに、条件が保たれていること、すなわち $d' \geq 2k'$ であることを確認します。ポイントは、遷移ができると $d$ は $1$ 減り、遷移できずに failure link を辿ると $d$ は少なくとも $1$ 増える、という点です。2回の遷移の試みのうち:

  • 両方遷移できず、failure link を２回辿ることになった場合:
    • 未処理文字が増え、$k'= k+1$, また、$d' \geq d + 2$。よって、$d' \geq d+2 \geq 2(k+1) = 2k'$。
  • 片方は遷移でき、もう片方は failure link を辿ることになった場合:
    • 未処理文字数は変わらず、$k' = k$, また、$d' \geq d$。よって、$d' \geq d \geq 2k = 2k'$。
  • 両方とも遷移できた場合:
    • 未処理文字が1文字減り、$k' = k - 1$, また、$d' = d - 2$。よって、 $d' = d - 2 \geq 2(k-1) = 2k'$。

以上より、不変条件を示すことができました。不変条件から、バッファが空でない場合、バッファ内のすべての文字の処理を完了したとしても受理状態に到達しないことが分かります。新しい文字で受理状態に到達できる ($d' = 0$) ためには $k' = 0$、すなわちバッファが空になる場合のみであることも分かります。このとき、未処理の文字はないため、現状態が普通の KMP と現状態と一致し、現状態が受理状態かどうかの判定で正しいことが分かります。

まとめ

いやぁ、文字列って本当に面白いものですね。

マニアックな文字列照合アルゴリズムに興味ある方はこちらもどうぞ。

参考文献

  • James H. Morris, Jr., and Vaughan R. Pratt, "A linear pattern-matching algorithm", Technical Report 40, University of California, Berkeley, 1970.
  • Donald E. Knuth, James H. Morris, Jr., and Vaughan R. Pratt, "Fast Pattern Matching in Strings", SIAM J. Comput., 6(2), 323–350, 1977. http://dx.doi.org/10.1137/0206024
  • Maxime Crochemore and Wojciech Rytter, Text Algorithms, Oxford University Press, 1994. PDF

  1. 文字列マニアの方は分かると思いますが、厳密には KMP ではなく MP (Morris-Pratt) の手法の解説となっています。KMP 法はボーダー配列の定義が若干違います。が、この記事で解説するリアルタイム版はどちらでも同じように正しく動作します。 ↩

  2. Crochemore & Rytter 両先生の Text Algorithms の定理3.5など。 ↩

  3. この後のオンライン設定と合わせる為に、パターンの開始位置でなく終了位置を出力するようにします。先頭位置を出力したい場合は、答えをパターン長分ずらせばよいだけです。 ↩

  4. 本当の KMP 法は $\Theta(\log m)$ 時間だが説明は割愛。 ↩

14
8
3

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
14
8