この記事は エンジニアと人生 Advent Calendar 2022 の19日目の記事です。18日目は h1d3mun3 さんの業務引き継ぎの際の考慮ポイントでした。
初めに
オフィスに通勤する回数が減った昨今ですが....
オフィスならどこにでもありますよね!自動販売機って!

(引用:ポッカサッポロ自動販売機)
当然のことながら、自社でもフロアには自販機があります。
問題点①
会社の自販機は電子決済オンリーの仕様になっています。
一見すると問題なさそうに見えますが...
(引用:電子マネー 楽天Edy)
楽天Edy は iPhone では使えないため、わざわざ Edy カードを持つ必要があります。Android の場合は、Google Pay 経由で使えるので、自分はこのためだけにデバッグ用に持っていた Android 端末を持ち歩いていました。
これでとりあえずはいいか!と思っていましたがまだ問題が...
問題点②
先に問題点だけ書くと、Google Pay が1000円単位でしかチャージできないことです。
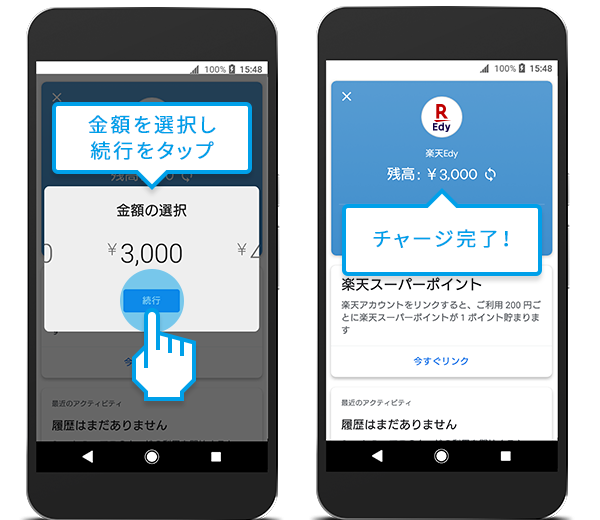
自販機の飲料は100円単位ではなく10円単位で違うため、ほとんどの場合は使い切らずに端数が残ってしまいます。
さらに弊社の場合は、自社ビル割引なのか?中途半端に1円単位で安くなっているいるため、さらに使い切るのが困難になっています。
【実際の写真】

理想
自販機で1000円を使い切りたいんじゃ!
ということで、これをプログラミングで解決していきます。
発想
1. 条件
1000円を使い切るための組み合わせを考えていくことになります。
まず、フロアにある自販機の飲み物を列挙していきます。
飲料一覧を見る
- おいしい水 天然水:89円
- Wilkinson Tansan:89円
- Wilkinson Tansan Lemon:89円
- ポカリスエット:89円
- Welch's FRUIT WATER LEMON:89円
- Welch's グレープ50ぶどう由来のポリフェノール:79円
- リポビタンD:96円
- 「届く強さの乳酸菌」W(ダブル) 「プレミアガセリ菌 CP2305」:96円
- モンスターエナジー:190円
- モンスターエナジー ウルトラ:190円
- モンスター パイプラインパンチ:190円
- ダイドーブレンド微糖 世界一のバリスタ監修:89円
- 極 ブラック 400g:96円
- 極 カフェオレ 285g:96円
- 極 微糖 285g:89円
- 極 ブラック 285g:89円
- ドトール カフェ・オ・レ:89円
- ワンダ ディープマウンテン:79円
- ワンダ 金の微糖:79円
- ワンダ モーニングショット:79円
- ワンダ 特製カフェオレ:79円
- ワンダ ごほうび抹茶ラテ
- カルピスウォーター:89円
- なだ万監修 日本茶:89円
- なだ万監修 ほうじ茶:89円
- 十六茶麦茶:89円
- 十六茶:89円
- 和紅茶:89円
- ドデカミン 500ml:96円
- ドデカミンストロング:79円
- 三ツ矢サイダー 500ml:89円
- 三ツ矢100%オレンジミックス:89円
- 三ツ矢サイダー レモン&ライム:79円
- 三ツ矢クラフトコーラ:79円
- すっきり1日分のマルチビタミン:79円
- さらさら毎日おいしくトマト:79円
- カルピス(R)THE RICH:79円
- バンホーテンココア:79円
- ロイヤルミルクティー:79円
これは値段別にすると4パターンに分類できました。
| 79円 | 89円 | 96円 | 190円 |
|---|---|---|---|
 |
 |
 |
 |
この4つの料金の飲料を無制限に選択して、1000円を作っていきます。
2. ナップサック問題から着想を得る
ここでパッと浮かんだのはナップサック問題に近いなと言う印象です。
- ナップサック問題とは?

n 種類の品物(各々、価値 vi、重量 wi)が与えられたとき、重量の合計が W を超えない範囲で品物のいくつかをナップサックに入れて、その入れた品物の価値の合計を最大化するには入れる品物の組み合わせをどのように選べばよいかという整数計画問題である。
(引用:ウィキペディア ナップサック問題)
ナップサック問題では、値段と重さの2つを考慮する必要がありますが、今回は値段だけなのでもう少し簡単かなと言う感じです。
さらにいえば、条件が1つなので部分和問題を考えれば良いことになります。
- 部分和問題とは?
与えられた n 個の整数 a1,...,an から部分集合をうまく選んで、その集合内の数の和が与えられた数 N に等しくなるようにできるかどうかを判定する問題である。
たとえば、「{1,3,7,10,13} の部分和で、和が 21 になるものは存在するか?」であれば存在する({1,7,13}である)、が答えである。また「{2,4,6,8,10} の部分和で、和が 19 になるものは存在するか?」であれば、存在しない(どんな部分和も偶数にしかならない)、が答えである。
(引用:ウィキペディア 部分和問題)
のっていた例題が今回考えたいこととまさに同じです。
- アプローチ
一旦、計算量のことは考えないとすると
-
深さ優先探索(DFS: Depth First Search) -
動的計画法(DP: dynamic programming)
あたりが方法として上がってくるかと思います。
3. 深さ優先探索を使って導く
- 理由
今回は
- 飲料4パターンの組み合わせ
- 合計値が1000円
と言う比較的小さい数字であるため、こちらのほうが簡単に実装できると思います。
概算値としても
- 飲料は1個で100円前後なので、10回前後の処理を行えば1つの処理が終わる
- 組み合わせは単純計算で
4^10 = 1048576 ≒ 100万なので長くても数秒程度
と言うことも考えて深さ優先探を選択しています。
- 実装
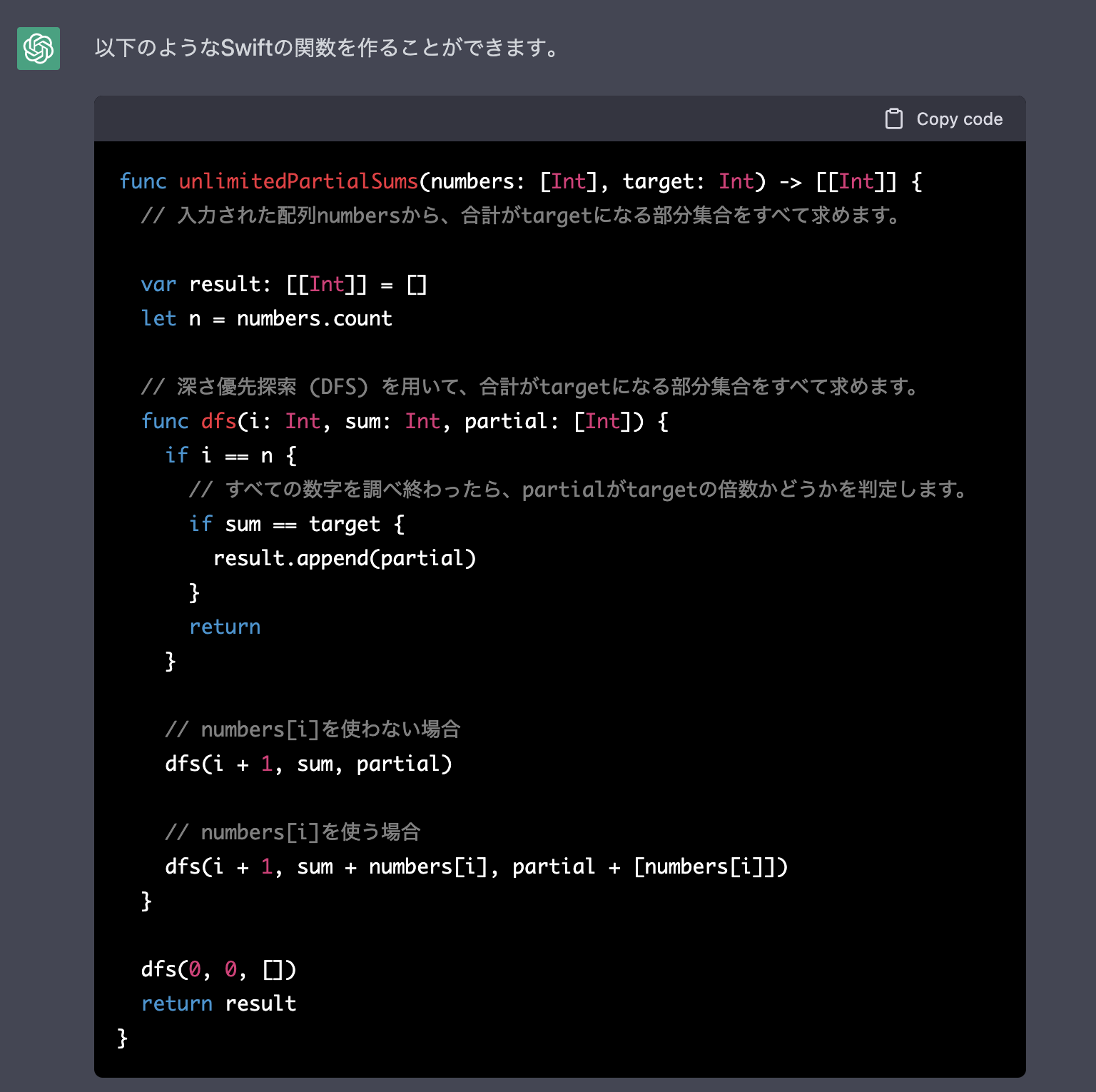
方針まで立てましたが、考えたくないので流行りの ChatGPT に投げました。
iOSエンジニアなので Swift で回答を求めました笑
そして実はこれ以外にも投げましたが...シンプルなこれが良かったです。
良さげな回答なんですが、結論から言うとこれでは条件を満たせていません。
(本件とは関係ないが、自動生成のコメントアウトまで日本語なのはちょっと感動)
上記のコードでは有限個の数しか満たせていません。そこでコードに少しだけ手を加えます。
func unlimitedPartialSums(numbers: [Int], target: Int) -> [[Int]] {
var result: [[Int]] = []
let n = numbers.count
func dfs(_ i: Int, _ sum: Int, _ partial: [Int]) {
- if i == n {
- if sum == target {
- result.append(partial)
- }
+ if sum == target {
+ result.append(partial)
+ return
+ }
+ if i == n || target < sum { // 無限に処理が発生しないようにする
return
}
dfs(i + 1, sum, partial)
dfs(i + 1, sum + numbers[i], partial + [numbers[i]])
+ dfs(i, sum + numbers[i], partial + [numbers[i]]) // 無限個選択を満たす
}
dfs(0, 0, [])
- return result
+ return Array(Set(result)) // 重複した処理を取り除く
}
これを実行すると
let result = unlimitedPartialSums(numbers: [79, 89, 96, 190], target: 1000)
print(result)
[
[79, 79, 79, 79, 79, 79, 79, 79, 89, 89, 190],
[89, 89, 89, 89, 89, 89, 89, 89, 96, 96, 96],
[79, 89, 89, 89, 89, 89, 96, 190, 190]
]
無事に結果を得られました!
※ 見やすいように改行しています
少し見ずらいので、式を Dictionary にして返すように変形しました。
- func unlimitedPartialSums(numbers: [Int], target: Int) -> [[Int]] {
- var result: [[Int]] = []
+ func unlimitedPartialSums(numbers: [Int], target: Int) -> [[Int: Int]] {
+ var result: [[Int: Int]] = []
let n = numbers.count
func dfs(_ i: Int, _ sum: Int, _ partial: [Int: Int]) {
if sum == target {
result.append(partial)
return
}
if i == n || target < sum {
return
}
+ var tmp = partial
+ tmp[numbers[i], default: 0] += 1
dfs(i + 1, sum, partial)
- dfs(i + 1, sum + numbers[i], partial + [numbers[i]])
- dfs(i, sum + numbers[i], partial + [numbers[i]])
+ dfs(i + 1, sum + numbers[i], tmp)
+ dfs(i, sum + numbers[i], tmp)
}
- dfs(0, 0, [])
+ dfs(0, 0, [:])
return Array(Set(result))
}
これを実行すると
let result = unlimitedPartialSums(numbers: [79, 89, 96, 190], target: 1000)
print(result)
[
[89: 5, 79: 1, 96: 1, 190: 2],
[79: 8, 190: 1, 89: 2],
[96: 3, 89: 8]
]
とても見やすくなりました!
どの組み合わせが良いのかわかるようになりましたね!
終わりに
ちなみに最近は自販機で楽天Pay(QR決済)が使えるようになったらしく、iPhone で済むとのこと。なんなら1000円以上は1円単位でチャージできるのでこんなこと考えなくて良いらしい。
というか、何買ったか逐一覚えてられないし、好きなものを縛られず飲みたいよな...
あ〜〜スタバ飲みて〜〜
こうして僕はオフィスの外のスタバに行くのであった。