本書は2017年4月1日にTeradata Japanのブログに掲載された内容を、再掲載したものです。
掲載内容の正確性・完全性・信頼性・最新性を保証するものではございません。
また、修正が必要な箇所や、ご要望についてはコメントをよろしくお願いします。
著者 山本 泰史 (やまもと やすし)
クラスター分析
クラスター分析、またはクラスタリングと呼ばれる手法は、各データサンプルが持つ変数の類似性に基づいて分類を行なう分析手法です。マーケティングへの活用の多くにおいて、各データサンプルとして顧客が対象となりますが、その際顧客を類似性に基づいて分類し、それをセグメントとして用いることが可能になります。類似性に基づくということは、同様の行動パターンや、同様の嗜好性、同様のパフォーマンスを有しているということであり、得られたセグメントは、データそのものの性質に基づいて分類されたという意味において意義があります。
図27は、横軸に直近未来店日数(現在を基準にしたときの最終来店日までの日数)を、縦軸に買上金額を配置し、それぞれの顧客が持つ行動/経済パフォーマンスを評価したものです。
それぞれにプロットされた点の集まりをかたまり、つまりクラスターとして認識した場合、ほとんどの方は3つのクラスターに分けて考えることと思います。左側の2点、真ん中の6点、右上の2点です。端的な判断をすれば、それぞれの距離が近いものは同じクラスターに、それぞれの距離が遠いものは異なるクラスターに分類されます。このような直感的理解に対して、小売業や通販業界では、RFMと呼ばれるマニュアルでのスコアリング手法を実施しています。これはRecency、Frequency、Monetaryの3つの指標に基づいて顧客を分類する手法です。例えば上述の例であれば、グラフを真ん中で4分割している直線(10日と15,000円に該当する直線)が、Recencyの観点で良いか悪いか、そしてMonetaryの観点で良いか悪いかを判別しています(簡素化のためFrequency - 一定期間における来店頻度は省略します)。このような形で人為的に引かれた線は、時に現実的な分類を表していないことがあります。顧客が3つのグループに分類されていることがグラフからは読み取れる一方、引かれた線はアフリカ大陸によく見られる国境のように人為的であり、本来同じクラスターに分類されるべき顧客群を分断してしまっています。現実的な分類を表していないのです。特に真ん中の6点は距離が近いにもかかわらず、ここでは2本の直線によって4つに分断されてしまいます。
もちろん既存のRFMの手法にも意味があります。例えばFrequencyに基づいて顧客を10等分したとき、上位10%の顧客と下位10%の顧客には同じ量の顧客が配置されることになり、2つの顧客群の比較を容易にしてくれます。また一定の値を人間が決定して分類した場合、これは人間が意味合いを推定するのを容易にしてくれます。例えばFrequencyスコアを10に分割し、もっともスコアの高いクラスターを「クラスター#1」として、ここに含まれる条件を「年間来店回数 >=52回」とした場合、クラスター#1は「毎週来店してくれる顧客」として理解することが可能です。またこのような分類方法は一貫性を提供してくれます。クラスター#1の顧客が減少すれば、自社に対する結びつきの強い顧客群が減少していることを意味します。このような手法はそれぞれに価値があり、各々顧客を評価する上で選択されるべき手法の1つです。
クラスター分析の強み - そしてこれは弱みでもありますが - は、データが変われば分類基準が変わることです。与えられたデータをもっとも論理的に分類できるということは、事実を正確に切り取ることに重きを置いているということです。特に利用する変数と、扱うデータが膨大になる場合、どのように分類していいか分からない場合もあります。また、人為的になされた分類が、本来有意義な分類基準や、膨大なデータの中で隠れてしまっている類似性を見逃してしまっている可能性もあります。これらを発見する際に、クラスター分析は威力を発揮することになります。また、クラスター分析を他の分析に先んじて実施することも有効です。これによってデータが持つ構造を事前に理解することができるため、変数選択や対象データ(例えばモデル作成の対象となる顧客群)の選択における知識を得ることが出来るからです。以降、クラスター分析の最も一般的な例としてK-Means法と呼ばれる分析手法についてご紹介します。

■K-Means法
K-Means法は量的変数(金額、数量、センチメートル等の定量的な変数)を対象とする際に利用可能な手法です。K-MeansのKは任意の数を意味し、分析者が何個に分類して欲しいかを任意に指定することから、Meansは算術平均(Mean: 与えられたサンプルを全て足してサンプル数で割るという、いわゆる平均のことです。Averageとも呼ばれます)から名前が付けられています。「K個の平均」を利用して分類する手法なのでK-Meansです。
ここではデータセットとして図28を用意しました。ある航空会社の顧客を想定し、一定期間における渡航回数と、支払金額を変数に用いています。いわゆるRFMにおけるFrequency値とMonetary値です。
そしてこのデータを散布図としてプロットしたのが図29になります。縦軸に支払金額を、横軸に渡航回数を配置しています。K-Means法ではまず、クラスターとして分割して欲しい数を任意に指定します。例えば「3つに分けて欲しい」といった指定が事前になされ、この指示に基づいて分割がなされます。ここでは、3つに分けることにしましょう。指定された数に基づいて、ランダムに点がプロットされます。ここでは点#1(2回, 500,000円)、点#2(6回, 500,000円)、点#3(10回, 500,000円)に配置します(図内■で表示)。そして、この3つの点を等間隔に区切る直線を引きます。これはいわゆる垂直二等分線と呼ばれるものです。そうすると、全てのデータサンプル、つまり顧客はいずれかの線で区切られ、分類されることが分かります。ここで点#1が含まれる区間をクラスター#1、点#2が含まれる区間をクラスター#2、点#3が含まれる区間をクラスター#3と呼ぶことにします。
これで、全ての顧客は取り敢えずいずれかのクラスターに含まれたことになります。ここで、同一のクラスターに含まれる顧客の平均を算出します。この平均こそが、K-Meansの「Means」であり、これがクラスターのへそ(基準点)になるものです。得られた平均はクラスター毎に存在することになり、平均は座標で表されます。そして最初にランダムプロットされた点#1、点#2、点#3を、それぞれこのクラスターのへそ(基準点)に移動させます。そして、もう一度この点と点の垂直二等分線を引き直します。幾名かの顧客はあるクラスターから、別のクラスターに再配置されることが分かるはずです。それぞれの基準点が移動したため、垂直二等分線が引きなおされ、同時にプロットされている各顧客が最も近しい基準点が変化したことを意味しています(縦軸と横軸のスケーリングが異なるため一見垂直二等分線に見えないこと、ご了承ください)。
このように、クラスターの基準となる点から垂直二等分線を引き、分割されたサンプルの平均をとり、その平均値となる点をにクラスターの基準点を移動していく、...というプロセスを繰り返していきます。この繰り返し作業は、平均値が変化しなくなるまで続けられ、平均値が変化しなくなったところで終了し、このときに得られた分類が、最終的なクラスターとなります。平均値が変化しなくなるということは、そのクラスターに属するサンプルが、クラスターをまたいで移動することがなくなるということを意味し、クラスターが安定した結果に行き着いたことを意味します。ここでは、2つの変数を利用しているため、2次元の平面で紹介していますが、n次元でも同様の作業がなされ、最終的なクラスターを決定することになります。またこの例では便宜的に点#1と点#3を分岐させる垂直二等分線を省略した段階から始めましたが、実際には全ての基準点間の組み合わせが検討され、複数のクラスター候補の中から、どのクラスターに属するかを決定する基準として利用します。反復計算終了後の最終的なクラスター分けは以下になり、それぞれの顧客はいずれかのクラスターに重複無く分類されることになります。
また反復計算の結果、各クラスターの平均は、図32のように移動していきました。この例においては、初期値を含め4回反復し、3回目と4回目が同じ結果であることから3回目で収束したことになります。データサンプル数と変数が膨大になるとき、反復回数はもっと多くなるはずです。



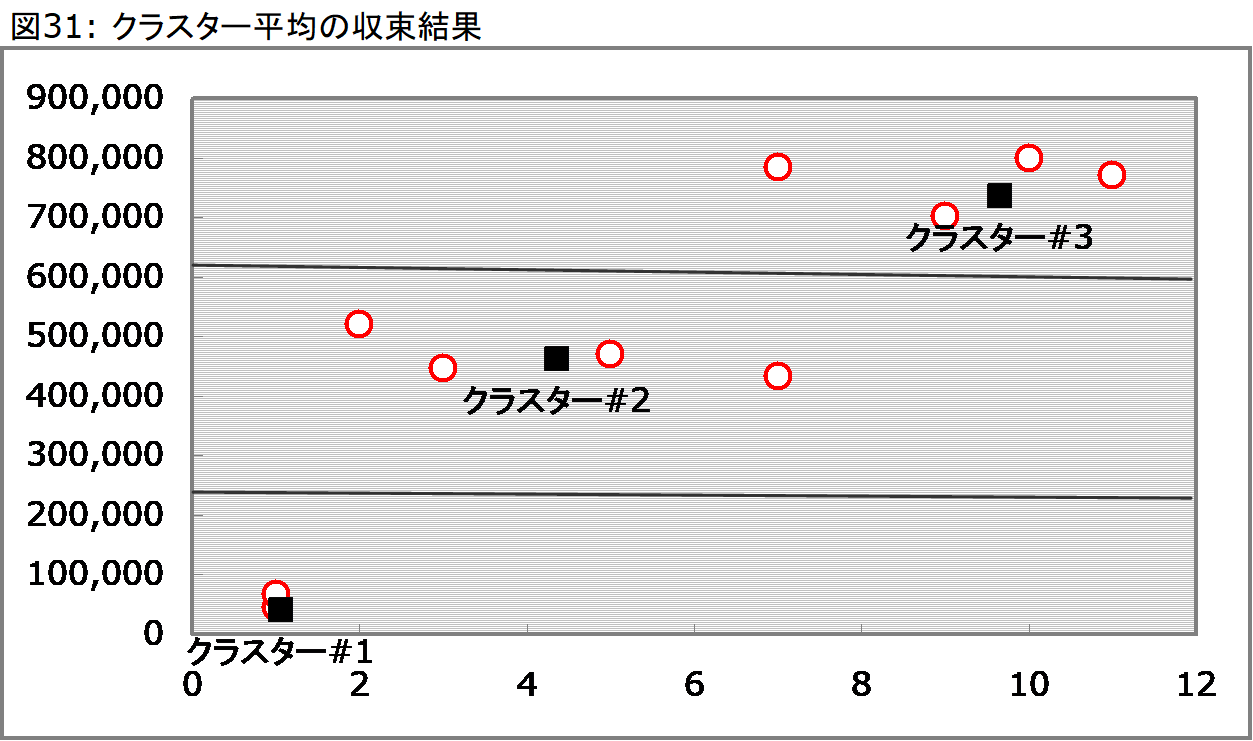

■クラスターの評価と解釈
以上、クラスター分析の考え方をご理解いただくために、既存のセグメントカットの典型例であるRFMのデータを用いて分割を行ないました。クラスター分析の結果、各データサンプルにはクラスター#がスコアリング結果として付与されます。これによって各データサンプルがどのクラスターに属するのかを理解できるようになります。しかしながらそのクラスターが、どのような傾向、特性を持っているのかという解釈は与えてくれません。上述の例でも明らかなように、ある傾きを持った直線によってクラスター分割されるため、単一変数の単一値を基準にクラスターが分割されている訳ではないからです。しかしながら各クラスター、各変数の平均がどこにあるかを理解することは可能であり、クラスター間で平均を比較することにより、それぞれのクラスター間の位置関係を評価することが可能となります。これらを見ていくことによって、各クラスターが何を意味しているのかを読み解き、解釈を付与することになります。
■クラスター分析の適用
例えばあるキャンペーン用に絞り込まれた顧客リストがここにあるとします。一定以上の反応確率スコアで絞り込まれたため、その観点においてこれらの顧客はある程度同質であると言えます。しかしながらこれらの顧客に対するキャンペーン案内に際して、悩んでいる点が1つあるとしましょう。リコメンドする商品を顧客ごとに変えることによって、顧客の反応度をより高めたいと思っているのですが、上述のスコアから見た顧客はある程度同質であり、商品を可変にする基準が見つけられないのです。このようなシチュエーションはオファーする商品だけでなく、メッセージの訴求ポイントやインセンティブオファーを可変にする際にも当てはまります。完全な個別対応ではなくとも、マスカスタマイズでこのような対応ができれば、それぞれの顧客から好反応を得られるかもしれませんが、それにはオファーAにふさわしい顧客と、オファーBにふさわしい顧客に選り分ける必要があります。
このような場合、既に得られている顧客リストに対して、オファー内容と関連性が高いと思われる変数を新たに結合し、データセットを作成してクラスター分析を実施すれば、インスタントなセグメンテーションが可能となります。認識された各クラスターを把握することによって、オファーを決定するためのヒントが得られるかもしれません。もちろん何も得られない可能性も有していますが、その顧客リスト内での多様性や、グルーピングの視点が見つけられれば、可変オファーの威力が増します。
RFMに代表される総合指標は、顧客の経済パフォーマンスや自社へのスティックネスを測る上で重要な指標であり、おいそれと分割基準を変更できるものではありません。基準を変更せず、一貫性を保つことによって、自社と市場の関係、そしてその変化を理解することが可能となるからです。しかしながら一方で、もっと短期的で、具体的な業務目標に直接的にリンクするようなセグメンテーション - 極論を言えばある特定目的の為の「使い捨て」セグメンテーションも本来必要なはずであり、それが出来れば便利なはずです。そしてこのようなとき、存在しているデータの、「データ間の距離」に忠実な形で分割してくれる手法の方が、目的に合致しています。このようなケースは上述したキャンペーンオファーだけでなく、例えば新たに進出した地域、支店、店舗における顧客層を理解するためにも利用可能です。新たに投入した商品やサービスに伴って獲得した顧客を理解するためにも、利用可能となることでしょう。クラスター分析は、このようにデータ自身が本来説明してくれる「未知の分割基準」を理解するために利用可能な手法です。そしてもちろん、得られたクラスターが一過性のものではなく、ある程度の普遍性を有するものならば、そのセグメントを継続的に管理すれば良いのです。