この本書は2017年4月1日にTeradata Japanのブログに掲載された内容を、再掲載したものです。
掲載内容の正確性・完全性・信頼性・最新性を保証するものではございません。
また、修正が必要な箇所や、ご要望についてはコメントをよろしくお願いします。
著者 山本 泰史 (やまもと やすし)
分析手法の分類と、単一変数の分析
データセットの準備が出来た段階で、データの分析に取り掛かることが可能となります。以降、主だった幾つかの分析手法について説明をしていくことになりますが、最初に各分析手法とそれぞれの性質について紹介をしておきます。
1.線形回帰分析
複数変数間の相関関係が直線によって説明できることを想定し、直線を引く関数式によって、従属変数を予測する手法。
2.ロジスティック回帰分析
線形回帰分析を修正した分析手法であり、S字型の曲線によって複数変数間の相関関係を理解し、その曲線を導く関数式によって事象の発生確率を予測する手法。
3.因子分析
大きく、狭義の因子分析と、主成分分析に分かれる。因子分析は複数変数間の背後にそれを導いた因子が存在すると仮定し、その因子を探る手法。一方で主成分分析は複数変数から導かれる傾向を比較的少数の合成変数で表すことによって、複数変数の持つ姿を明らかにする手法。
4.クラスター分析
ある複数のグループに各行を分類する手法。クラスター中心からの距離に基づいて複数変数間に存在するデータの密集と過疎の状況を理解し、分岐を行なう線引きの実施によって分類する手法。
5.決定木
IF THEN(もし~が発生したら、その次に~が発生する)形式でデータを分類/予測する手法。各行の類似度合いに基づいて行の分類を行い、その分岐条件をIF THENのモデルで記述する。当該モデルを用いて分類、もしくは予測に活用可能。
6.アソシエーション分析
IF THEN形式で、複数事象の同時/誘発発生頻度を理解し、事象間の関連性の高さを理解する手法。得られたIF THEN形式に対して発生確率が得られ、これを用いた予測に活用可能。
他にも多くの分析手法が存在しますが、この資料では以上の6つについて説明を行なっていくことにします。それぞれの分析手法には違いがあり、時と場合によって適切な分析手法を選択することになります。適用の仕方は様々であり、「こういうケースではこの分析!」と固定概念を植えつけるべきではないですし、それを超えたところに新しい、そして価値ある適用例が見つかるものであるとも感じますが、あくまで筆者による個人的観測という意味で、分析手法選択基準について記述します。
■予測に用いる分析手法の選択
上述の分析手法の中で、線形回帰分析とロジスティック回帰分析、決定木、そしてアソシエーション分析は予測に適用可能な手法と位置づけられます。線形回帰分析の予測値は定量的なデータとなり、一方でロジスティック回帰分析は、発生確率を予測する手法です。予測したいことが何かによって手法の選択がなされます。一方、決定木とアソシエーション分析における予測はIF THEN形式であり、発生確率や予測値そのものよりも、どのような事象が発生するかという内容に主眼が置かれます。決定木であれば離反顧客のIF THEN文から離反可能性の高い顧客の行動を予測することが可能ですし、アソシエーション分析では発生事象間の関連性から、次にオファーするべき内容、次に打つべきマーケティングアクションは何かを予測することになります(実際には発生確率に関連する指標を表示するので、分析手法自体は関連性の記述を行い、それを見て分析者が予測することになります)。
■分類に用いる分析手法の選択
決定木は分類にも利用可能です。類似の行動パターンを持つ顧客はある分岐条件に対して同じ分岐を行なうため、最終的に得られた結果は顧客の分類結果となります。一方でクラスター分析は純粋にあるクラスター数に分類するとしたときに最も納得が行く形に収まるよう、分類を行ないます。人間が持っている既成概念に囚われない分類手法を探す場合、クラスター分析の方が適しています。また、因子分析、主成分分析で得られた結果を元に分類を行なうことは可能ですが、因子分析、主成分分析の主眼は、どちらかというとデータセットを用いて、新たな変数を作成し(新たな変数に絞り込み)、それによって元々与えられたデータセットの見晴らしを良くすることに置かれています。つまりどのような変数が得られるかという点に着目するのであれば、因子分析、主成分分析が適切な手法となります。
■複数手法の選択
上記の選定条件はそれぞれのケースを想定した場合ですが、実際の業務プロセス上で考えた場合には、複数の分析手法が併用されることになります。もしあなたが優良顧客向けのプレミア・プログラムを検討しているとします。そのとき、まず優良顧客を理解するためにクラスター分析でセグメンテーションを行い、彼らを正確に識別/理解するための指標獲得に主成分分析を利用し、さらに決定木で彼らの行動特性や傾向を掴み、最終的にキャンペーン計画を立てた後でロジスティック回帰分析を用いて反応予測を行なう...といったことは良くある話ですし、このような業務の流れの中で単一の分析手法に固執していたのではすぐさま立ち行かなくなってしまいます。何を差し置いても気にしなければならないのは「ビジネスのテーマ」であり、「分析から何を得たいのか」です。それに伴って必要なデータが選別され、必要な分析手法が選択されることになります。そして実務のコンテクストの中で、必ずしも単一の分析手法が全てを解決するものではありません。
■分析手法の基礎構造
ちなみに各分析手法のうち、最初の3つ(線形回帰分析、ロジスティック回帰分析、因子分析)は統計的手法や多変量解析と呼ばれ、データマイニングと呼ばれる言葉が存在する以前から、統計学の実際活用の方法論として発展してきました。一方で残りの3つ(クラスター分析、決定木、アソシエーション分析)は人工知能的手法、もしくは機械学習的手法と呼ばれ、どちらかというと確率的な観点からデータを理解しています。またこの手法は相対的に、力任せに計算を繰り返すことによって解を得る傾向の強い手法であり、コンピューターテクノロジーの進化に大きく依存して発展してきた手法です。また、多変量解析という言葉は、多くの、つまり複数の変数(=変量)を解析するという意から生まれています。そして多変量解析は、単一の変数それぞれについて理解し、続いて複数変数間の関係を理解するという構造で成り立っています。このような基礎的な分析、つまり分類や予測をするのではなく、そのデータが何を表しているかを記述する統計分析手法を、記述統計と呼んでいます。
■単一変数の分析
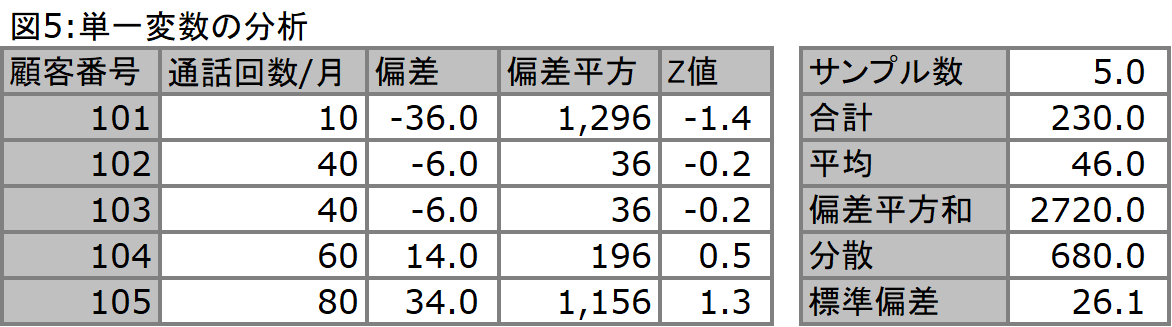
単一変数の分析に用いられる指標の多くは一般的に、我々が既に理解している指標です。図5のようなデータが存在するとき、この変数(通話回数/月)の平均(Mean, Average)は、(10+40+40+60+80)/5にて算出されます。これは各データサンプルの合計に対して、サンプル数で割って導き出されます(平均値は46)。それでは、このデータはどのような特徴を持つかを説明しなければならない場合、どのような特徴で以って説明をすることができるでしょうか。平均値は重心とも形容され、大体どこら辺にデータが落ち着いているかを意味します。また、最小値(Min)、最大値(Max)という観点では、それぞれ10(顧客#101)、そして80(顧客#105)として表され、この差は範囲(Range: 70 = 80 - 10)と呼ばれます。これらにプラスして、中央値(Median)、最頻値(Mode)等によっても特徴の一側面が説明可能です。中央値は、昇順/降順で並べた場合にデータの真ん中に位置するサンプルの値を意味します(以下の例では40(顧客#103))。最頻値は、最も多く発生している値を意味します(以下の例では40(顧客#103及び104から))。
一方、#101から#105に至るデータは「ばらけて」おり、このばらけ度合いを説明するのが「分散(Variance)」です。分散の算出は、平均値からの乖離度合いを測ることから始まります。この乖離度合いを偏差と呼び、上述のように平均値は46となります。46からの偏差は#101から#105において、それぞれ(サンプル値 - 平均値)で算出されます。基本的にはこの偏差の平均的な数値を導き出したいのですが、ご覧頂くと、幾つかの値はマイナスの値をとっていることが分かります。シンプルに平均をとる場合、これらの値を全て合計しようとすると、マイナスとプラスの値が打ち消しあい、本来存在する乖離度合いを説明できなくなってしまいます。このため、それぞれの残差を2乗し、これらの値を絶対値として扱えるようにします。この合計値を(サンプル数-1)で割ったのが「分散」となります(ここでの偏差平方和、つまり合計は2,720、サンプル数は5であるため、分散は2,720/(5-1) = 680)。分散は、特定の単位を持つわけではありませんが、他のデータとばらつき度合いを比較する際に利用することが可能です。また分散の平方根(ここでは√6801/2 = 26.1...)が平均からの乖離の平均、つまり平均からどの程度散らばっているかを説明しています。この26.1...は、単位として変数と同じ単位になります(ここでは通話回数/月)。従って46プラスマイナス26.1...が46を中心とした分散の真ん中を表しているということになります。この分散の平方根を「標準偏差(Standard Deviation)」と呼びます。
ちなみに、標準偏差を分母に、そしてそれぞれの偏差を分子に置いて算出されたのがサンプルの標準化された値です。この値はZ値とも呼ばれますが、これは標準偏差を基準にしたデータの分散状況を表現しています。