本書は2017年4月1日にTeradata Japanのブログに掲載された内容を、再掲載したものです。
掲載内容の正確性・完全性・信頼性・最新性を保証するものではございません。
また、修正が必要な箇所や、ご要望についてはコメントをよろしくお願いします。
著者 山本 泰史 (やまもと やすし)
因子分析
回帰分析において見られたように、複数の説明変数の間には様々な関係が存在します。近似の傾向を持つものもあれば、何らかの隠れ変数が変数間に存在しているのではないかと思わせるものもあります。因子分析はこれらの関係を整理し、それぞれの変数のレベルを適切に修正することによって、新たな変数を作り出します。つまり新たな変数を構築し、その変数を以って1.顧客やその行動を評価する指標値とすること、2.各変数を表出させる原因となった変数とすることが、因子分析の目的になります。ここで得られた変数は他の分析手法に利用する変数の候補とすることが可能であり、事実、数多くの変数候補を集約するために利用される場合があります。因子分析と大きく括っていますが、この手法は主成分分析と、いわゆる狭義の因子分析の2つによって成り立っています。そして1.の目的に基づいて新たな変数を構築する場合には「主成分分析」、2.の目的に基づいて新たな変数を構築する場合には「因子分析」が利用されます。
主成分分析は、説明力の高い(与えられたデータの多くを説明している)変数(主成分)を導き出し、その説明度合いを表すものです。よく食品の栄養成分表に記載されるように、どの成分が何%を占めているのかを導き出します(もっとも、そんなに単純なものではありませんが)。主成分分析によって、一般に説明変数は主成分に統合され、より少ない変数(主成分)でデータを説明させることが可能となります。広義にとるとこの主成分もデータを説明可能な因子の1つであるため、ここでは因子分析の中に含んでいます。
これに対して狭義の因子分析は、「与えられたある変数は、純粋にある単一の原因によってもたらされたものではないのではないか?」という疑念の上に成り立っています。与えられた複数の変数、つまり結果は背後にある同一の原因に影響を受けており、また複数の原因がある単一の変数に影響を与えているのであれば、我々は背後にある原因=隠れ変数の存在を見透かすことが出来ます。このような変数を「因子」と呼び、この因子を見つけ出すのが因子分析の目的となります。以降、それぞれについて説明をしていきます。
■主成分分析
主成分分析は、与えられた幾つかの変数を用い、合成することによって「合成変数」を作成し、この合成変数を以ってデータセット全体を説明しようとする手法です。合成変数とは、結局のところ主成分のことなのですが、このような言葉を使うのには理由があります。変数が仮に3つで、それぞれx1、x2、x3としたとき、合成変数はa1x1 + a2x2 + a3x3にて表されます。つまり、与えられた幾つかの変数を使って、新たな変数を作り出すのです。それぞれの合成変数の中身を考えたとき、変数以外はa1、a2、a3の係数で示されます。これはそれぞれの変数に対して重み付けがなされていることを意味し、重み付けされた各変数をそれぞれの成分とした形で新たな合成変数を導き出すこととなります。このような成分構成で説明される合成変数を「主成分」と捉え、扱っているのが主成分分析です。
純粋にイメージとして考えた場合、例えば優良顧客はどのように定義されるべきかを考えると想像しやすいかもしれません。定義の仕方は色々ありますし、単純にたくさんお金を費やしてくれる顧客を「優良顧客」と定義することもできなくはありませんが、ここでは、優良顧客を年間支払い金額(x1)、利用年数(x2)、そして年間発生コスト(x3)の3つで捉えることにします。それぞれの変数はどのように組み合わせれば、「優良顧客」から「非優良顧客」までを1つの合成変数で説明できるようになるでしょうか。単純には(x1-x3)が単年の利益金額であり、これにx2を掛け合わせると顧客の利益貢献金額が算出されます。つまり(x1 - x3) * x2が累計利益貢献金額であり、これらの変数は一般に言われるLTV(Life Time Value : 顧客生涯価値)の基礎数値として利用可能な指標です。顧客はある指標を用い、様々に捉えられますが、それはある側面を表すものでしかありません。主成分分析ではこのような式ではなく、a1x1 + a2x2 + a3x3のようにシンプルな1次式のみを扱いますが、このように各変数を組み合わせて総合指標を作成します。これを主成分として捉えるのが主成分分析となります。また、主成分分析で得られた合成変数は他の分析手法でも用いられます。何らかの傾向を説明している変数群を束ね、ある単一の変数を得ることが出来るならば、この変数は他の分析手法にとっても価値があるものだからです。
■主成分分析の考え方
図13(次ページ)のような2変数 * 3データサンプルのデータセットを考えます。分かりやすくするため、x1を携帯電話の通話料金、x2を携帯メールやインターネットアクセスのパケット料金とし、それぞれのデータサンプルを3名の顧客と見立てます。ここで、極めて乱暴ですが、これに対して主成分分析を試みることにします。単純に合成変数の候補として、A = (x1 + x2)と、B = (x1 - x2)の2つの主成分しか考えないとしましょう。どちらが主成分分析として優れているかを考えます。通常、毎月の請求料金はAで示されるため、Aがふさわしいと考えるかもしれません。しかしながら主成分分析の観点から考えた場合、Bの方が優れた情報を内包しています。なぜなら、Aの指標では3名の顧客の違いを識別できないことが実際のデータ値から明らかであるからです。言い換えれば、それぞれの顧客が持つ、通話料金とパケット料金の構成比の違いをここではスポイルしてしまっているのがAということになるからです。
一方でBは、3名の違いを明確にしています。我々が通常有している価値観としては大きいほうが好ましい(もしくは小さいほうが好ましい)といった価値観に合致するような変数の作り方を考えたくなりますが、主成分分析においては、このような価値観は後から考えます。主成分分析のアルゴリズムはまずデータをあるがままに把握し、そのデータが持つ構造が際立つように変数を作成することを試みます。この変数が持つ構造をもっとも分かりやすく際立たせるために用意されたのは(x1 - x2)という指標作成処理であり、この結果作成された指標に対して、どのような説明が可能であるかは分析者、つまり人間に委ねられる形となります。ここで得られた指標は、プラスの方向に振れれば通話料金が多い傾向にあり、マイナスの方向に振れればパケット料金が多い傾向にあり、0に近しければ、通話料金とパケット料金のバランスが良い顧客であるということが読み取れます。つまり、このような形でデータセットの見え方、つまりコントラストが最も際立つ形で変数集約を行なうのが、主成分分析の考え方となります。

■変数が持つ構造を際立たせる
コントラストを最大化させるような変数を作り出すという観点では、図14のように考えていただくと分かりやすいかと思います。
変数Aは、図14における視点Aの立ち位置からデータを眺めているようなものです。全て同じ値であり、全て重なって見えます。つまり違いが分かりません。これに対して変数Bは視点Bからデータを眺めています。それぞれのデータがもっとも見えやすい位置であり、もっともばらついて見えます。
このようなばらつきを示す指標として用いられるのが、「分散」です。視点Bからデータを眺めるとき、最もばらつきが大きくなります。つまり分散が最大化されます。一方視点Bでデータを眺めるためには、その矢印に対して垂直に引いた線(薄い色で追加した線)でデータを捉えれば、分散は最大化されることになります。
分散を最大化させるような式a1x1 + a2x2を求めることが、そのまま合成変数を得ることになります。その際の手順として、以下のような手順を踏むことになります。
- このデータセットの分散/共分散行列を算出する
- 1.を用いて、固有値/固有ベクトルを算出する
- 2.の固有ベクトルを用いて、各データサンプルの主成分得点を得る
式a1x1 + a2x2において、各xはデータセットに記されている値であるため、まず求めなければならない値は各aの値です。2.の固有ベクトルが各aの値を意味し、そして得られた固有値が分散の大きさを意味します。そして得られたaの値と、データセットにあるxを利用することによって、主成分得点が得られることになります。以降で、順を追って説明を加えていきます。

■分散/共分散行列
分散はある単一変数における平均値を考え、続いて各データの平均からの偏差(各データ -平均)の2乗を全て合計した値(偏差平方和、偏差2乗和)を、(データサンプル数 -1)で割って求めます。これが分散であり、ばらつきに対するイメージを我々に与えてくれます。一方で共分散は、この例における2変数x1とx2における共同のばらつきを意味します。共分散においても数字の大きさが分散の大きさを表しますが、一方で共分散はマイナスの値もとり、このときにはその分散の構造が右肩下がりの分布になっていることを意味します。ちょうどここで対象としているデータセットの分布は右肩下がりとなっています。共分散の算出方法は、各データの平均からの偏差をデータサンプルごとに掛け合わせ、そしてそれを足した値(偏差積和)に対して、(データサンプル数 -1)で割ることによって求められます。この例では、図15のようになります。
これを以下のような縦横対称の形で配置したのが分散/共分散行列です。
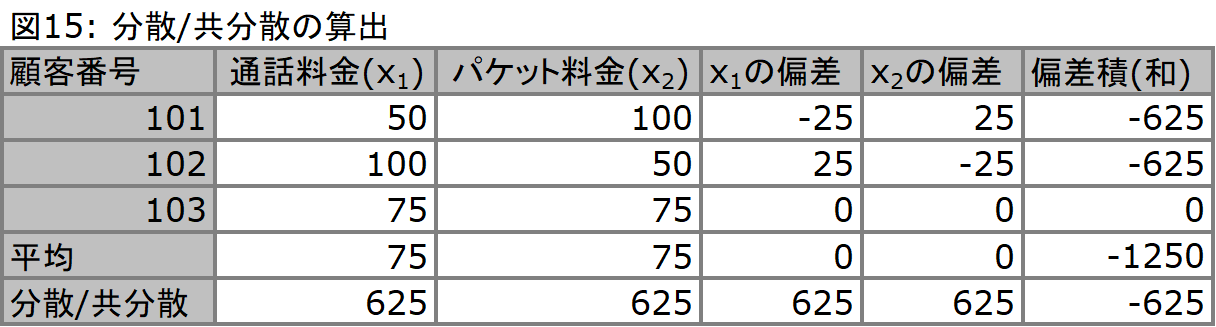
詳細な意味合いは割愛しますが、これがこのデータセットが持つばらつきの構造を表した行列となっており、固有値/固有ベクトルを求める上で必要になります。この行列は、例えば変数が4つであれば4行*4列の行列となり、やはり同じようにデータが縦横対称に配置されます。x1とx1がぶつかる部分にはx1の分散を、x1とx2がぶつかる部分にはx1とx2の共分散が配置されます(図16では2箇所存在します)。フットボールゲームの総当たり戦に使われる星取表と同じ要領です。

■固有値/固有ベクトル
分散/共分散行列を用いて作成するのが、固有値/固有ベクトルです。固有値は変数の数だけ作成されます。また、固有ベクトルは固有値毎に変数の数だけ作成されます。固有ベクトルは、与えられたデータの分散がどちらの方向を向いているかを定義しています。言わば「方向」を意味する指標です。そして固有値は、その方向に対してどの程度の大きさで分散が広がっているか、つまりばらついているかを意味しています。主成分分析は分散を最大化するような線で、各変数を構築しなおすことであり、それは言い換えれば固有値が最大になる線の方向(固有ベクトル)で各変数を構築しなおすことです。固有値/固有ベクトルの算出は複雑になる為、ここでは割愛しますが、上記で得られた分散/共分散を用いると、次のように固有値/固有ベクトルを得られることになります(図17)。

左側の固有値は大きく、これは最初に意図した直線、つまり分散が最大になるような直線を意味しています。これに対して直角に引いた直線を考えた場合、この方向への分散は0ですので、その次にある右側の固有値が0になるというのも説明がつきます。それぞれに固有ベクトルが記載されていますが、この値が、a1及びa2となります。これによって式a1x1 + a2x2を構成する要素が全て出揃ったことになります。
■主成分得点

各データサンプルを式a1x1 + a2x2に代入して得たのが固有値1及び固有値2に関する主成分得点です(図18)。
固有ベクトルは、純粋にその方向を考えるという観点からa12 + a22 = 1(この例では(-0.707)2+(0.707)2 = 1)となるようデザインされており、そのため、単純にx1 - x2(つまりa1=1、a2=-1)といった変数とはなりませんでしたが、当初の想定どおり固有値1は分散を最大化し、通話料金偏重ユーザーとパケット料金偏重ユーザーをプラスとマイナスに振り分けるよう主成分得点を算出しました。また固有値2は0であったため、主成分分析という観点では説明可能な価値を有していません。固有値2は固有値1に対して垂直に伸びる直線の分散を意味し、つまりこの直線の長さ、大きさが0であったことを意味します。そのため、この固有値2の主成分得点は全て同値に落ち着いたこと考えると、納得がいくものです。主成分分析の目的は新たな合成変数を構築することによって、そのデータセットを説明することであると述べました。ここで得られた式a1x1 + a2x2がそれに当たりますが、その式に各データサンプルを当てはめることによって、各データサンプルの特徴を理解することも可能となります。
■寄与率
上述のように、固有値はそれぞれに大きさが異なります。例えば10個の変数を持つデータセットであれば10個の固有値が得られますが、それぞれに大きさは異なり、10個よりも小さな数の固有値(主成分)で全体の傾向を説明できることに主成分分析の価値があります。合成変数を作るということはつまり、少ない変数でより多くを説明できるということであり、それはすなわち、主成分分析によって得られた主成分の数が、元々の変数の数よりも少なくなることに意味があります。上述の例において固有値2は不要であり、固有値1に集約できたことが主成分分析の価値なのです。
そして、どのくらいの説明が出来ているかを判断する基準指標として、「寄与率」という指標が存在します。この寄与率は線形回帰分析において利用されている寄与率とは異なり、分母に各変数の分散の和を、分子に作成された主成分の分散の和を用いて算出されます。作成された全ての固有値に対応する主成分を採用する場合、寄与率は1になりますが、それでは分母と分子に利用されている変数、主成分の数が同じとなり、意味がありません。分子に用いる主成分が少ないにも拘らず、寄与率が例えば0.8以上の値であれば、それは少ない主成分で充分なデータの説明をしているということになります。ちなみに、ここまでで利用してきた例の場合、主成分1の分散は1,250(分子)、主成分2の得点は全て同値であるため分散は0となっています(図18)。これに対して変数x1とx2の分散はそれぞれ共に625です(図15)。従って2つの分散の総和は1,250となり、これを分母に算出された寄与率は100%となります。つまり主成分1で完全に2つの変数を説明できていることを意味しています。
■因子分析
ヒトは何かの事象に直面したとき、その原因を突きとめ、納得しようとします。例えば他人の性格が出るような行動に対峙したとき、「山本が二重人格なのはAB型だから」といった具合です。表出する性格が全て4つの血液型に起因するものかは分かりませんが、変数を発生事象/観測結果と捉え、それを引き起こした因子を探り出そうとするのが、(狭義の)因子分析の目的となります。因子分析において各データは、因子得点、因子負荷量、独自因子(誤差)にて説明されることを前提としています。因子得点は上述の例でいうAB型であり、これが因子の役割を意味します。これに対して因子負荷量は、観測結果である各変数に対する「影響力」を意味します。変数が例えば「優しさ」と「二重人格」であるとした場合、AB型という因子は「優しさ」にはあまり影響を与えず、「二重人格」には強く影響を与えるといった具合です。そして独自因子は、そのデータが特有に持つものであり、因子分析にて説明しきれない部分です。この例をそのまま用いれば、以下のようなイメージで分解できることになります。ここでいう「山本」がデータサンプルです。因子負荷量は因子に与える影響であるため、他のデータサンプルにも共通して適用されます(例えば別のサンプル:ジキル博士に対する因子負荷量、優しさ=0.1、二重人格=5)。しかしながら因子得点は各データサンプルが固有に持つ値であり、山本の因子得点(=2)と、他のデータサンプルの因子得点は異なります(例:ジキル博士=10)。結果、表出するデータ値も異なることになります。
山本の[変数:優しさ=0.3]= [因子得点:AB型=2] * [因子負荷量:優しさ=0.1] + [独自因子=0.1]
山本の[変数:二重人格=10.2]= [因子得点:AB型=2] * [因子負荷量:二重人格=5] + [独自因子=0.2]
■因子分析の流れ
ここでは図19のような、あるCDショップの顧客5名に関する、ご覧の3ミュージシャンのCD購入数量データを用います。音楽は非常に嗜好性による影響が表れやすい商品であり、ここでは顧客のミュージシャン選択傾向から背後に存在する嗜好性を因子として見つけることを目的とします。そのため、ここでは各ミュージシャンのCD購入数量が変数となっています。
因子分析においては標準化されたデータセットを用意し、これを用います。標準化は変数に対して、((変数 - 平均)/標準偏差)の処理を行うことによって得られます。処理の目的はこれらのデータを全て平均0、標準偏差1のデータに変換しなおすことにあります。この処理を行なうことによって得られたデータが図20になります。


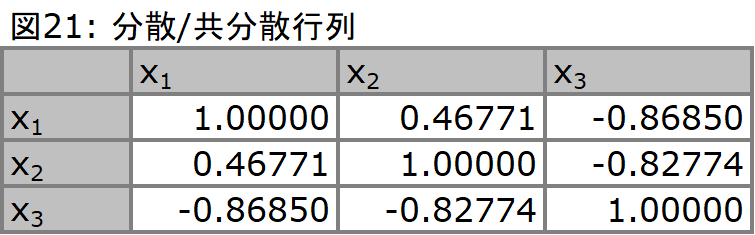
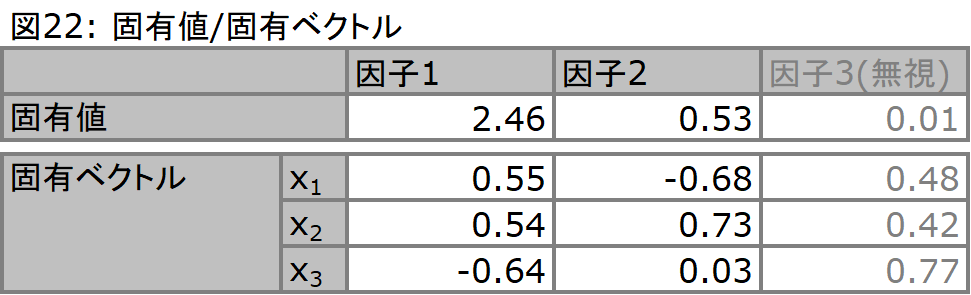
続いて、このデータセットの分散/共分散行列を作成し(図21)、そこから固有値/固有ベクトルを得ます(図22)。結論から言えば、ここで得られた固有値/固有ベクトルが因子を意味しています。得られた固有値は3つありますが、固有値1(因子1)と固有値2(因子2)でほとんどを説明しているため、固有値3(因子3)は無視することにします。各固有値の大きさが分散の大きさを意味し、固有値1及び2で、全体の99%以上を説明しているからです。ここまで - つまり分散/共分散行列から固有値/固有ベクトルを求め、データのほとんどを説明している固有値/固有ベクトルのみを残し、それ以外は無視する(捨てる) - までのプロセスは、主成分分析と同じです。つまり分散という観点から、データをよく説明している固有値/固有ベクトルを抽出することが、因子分析においても同様に必要な作業となります。
一方、ここからは主成分分析と因子分析では異なります。主成分分析において、変数は各主成分にて全て説明されました。これは言い換えれば、主成分分析は存在するデータを説明するような合成変数を作り出すことに主眼が置かれていることを意味します。しかしながら因子分析は、背後に存在する原因を変数として浮き上がらせることに主眼が置かれています。従って、与えられたデータの全てを因子で説明する必要はなく、逆に説明しきれない部分も存在することを意味しており、この説明しきれない部分を検討外にすることによって、因子が浮かび上がる構造になっています。分散/共分散行列で、各変数の分散は1と表示されています(図21)。これは標準化されたデータセットに変換したためですが、各因子によってもたらされた分散の合計は必ずしも1ではなく、これを推定する作業が必要になります。一方で因子負荷量は、各固有値の平方根に対して固有ベクトルを掛け合わせた値によって推定され、「各因子によってもたらされた分散の合計」は、各因子負荷量の2乗を合計した値によって推定されます。詳細は割愛しますが、関係は以下となります。
「各因子によってもたらされた分散の合計」 = (因子1負荷量)2 + (因子2負荷量)2 因子負荷量 = 固有ベクトル*√(固有値)
「各因子によってもたらされた分散の合計」は、「共通性」と呼ばれます。共通性の正確な値は、反復解法によって得られます。元々の分散/共分散行列にこの値を代入し、固有値/固有ベクトルを抽出する作業を何度も繰り返し、「共通性」がある一定の値に収束するまで反復計算を行ないます。
図23は、固有値/固有ベクトルから因子負荷量、共通性を導き出した表です。そして得られた共通性を、元々の分散/共分散行列の分散部分に代入しています。ここからさらに固有値/固有ベクトルを導き出す作業が繰り返されます。今回はこの作業を10回繰り返しました。結果、例えば変数x1の共通性は、以下のように収束しました。充分に収束した時点で得られた因子負荷量が、最終的な因子負荷量になります。また同時に、共通性、つまり分散に関してもある値に収束し、これが因子によってもたらされた分散となります。元々の変数が持っていた分散は1であったため、分散に関して以下が成り立ちます。


変数の分散 = 1 = 「各因子によってもたらされた分散の合計」 + 「独自因子(誤差)の分散」
従って、ここで行なわれた反復解法は、共通性の中に含まれていた独自因子の分散を吐き出し、純粋に各因子によってもたらされた分散に純化していく作業であるとも言えます。
■因子の特定と解釈
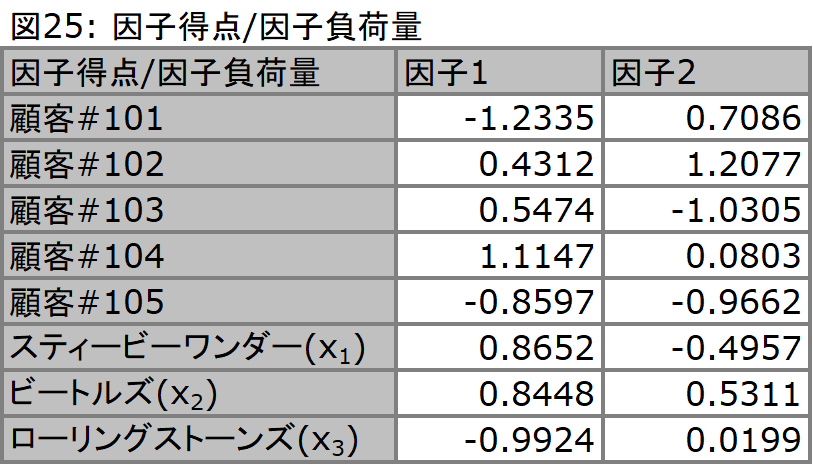
ここまでで因子負荷量から得られた因子得点が次ページの図25です。一方で因子得点は、得られた因子負荷量を元に、元々のデータセットと分散/共分散行列に対して逆算を仕掛けていくことによって導かれます。仕組みについては割愛しますが、以下のそれぞれを行列と見立て、行列演算を用いて算出されます。
(データセット) * {(分散/共分散行列の逆行列)*(因子負荷行列)} = 因子得点(の行列)
ここで、最終的に得られたデータとしての因子負荷量と、因子得点を利用して、グラフを作成します。それぞれの顧客(各データサンプル)と、それぞれのミュージシャン(各変数)は、いずれも2つの因子に影響を受けており、縦横の両軸に因子をとって散布図を作成した場合、その影響の度合いによって偏って配置されます。ここからは、人間が因子の意味を判断し、その因子に何かしら名前を付けます。
得られたグラフから判断するに、これら顧客の購入数量の背後に存在する因子は、以下の2つが想定されます。
因子1 -横軸:
音楽的傾向がメロウか、ソリッドか
ビートルズ、スティービーワンダーは美しいメロディラインが特徴の曲を多く書いており、比較的メロウな音像の印象があります。一方でローリングストーンズは、激しいリズム&ブルースが中心であり、比較的硬質で低音を強調した演奏がその特質となっています。横の軸がもたらしている尺度は、このように彼らの紡ぎだす音の構造に起因していると考えられます。
因子2 -縦軸:
黒人音楽の要素
マイナスが大きければこの要素が強いと想定されます。ローリングストーンズのメンバーは白人ですが、リズム&ブルース、ソウルミュージックのような米国1950-60年代の黒人音楽に強く傾倒した音楽を演奏しており、ビートルズよりもこの傾向が強いと言えます。また、スティービーワンダーはモータウンレコードの花形であり、黒人音楽の歴史において重要な位置づけを持つ巨人の1人であり、また言うまでもなく彼の音楽は黒人音楽そのものです。ビートルズと正反対の値をとっていることからも、縦軸0の横ラインがエボニーとアイボリーを音楽的に分けているとみなすことができますが、一方でこの軸が意味している因子の強さは、因子1に比べて大きくありません。顧客が感じる音楽的な近しさは、音楽的なバックグラウンドでもなく、同じスウィンギン・ロンドンのムーブメントから生まれ出たという歴史的一致でもなく、メロディの美しさを重視するか、反復的なリズムのもたらす興奮を重視するかに依存していることが見て取れます。またプロットされた各顧客を見た場合、彼/彼女の好みも見えてきます。例えば顧客#102、#103、そして#104に対するリコメンデーションを考える場合、秀逸なメロディメイカーが創る作品がその候補となることでしょう。

■元の変数との突き合わせ
元々この分析に利用したデータセット(標準化されたもの:図20)において、顧客#101のx1に対する変数は、-1.43でした。この値は因子得点と因子負荷量、そして独自因子(誤差)によって以下のように算出されます。また、-1.43と得られた-1.41855の差分が独自因子とになります。
-1.43
= 因子得点(顧客#101、因子1) * 因子負荷量(x1、因子1) + 因子得点(顧客#101、因子2) * 因子負荷量(x1、因子2) + 独自因子
= (-1.2335) * (0.8652) + (0.7086) * (-0.4957) + 独自因子
= -1.41855... + 独自因子
■主成分分析と因子分析の違い
主成分分析の目的は、与えられたデータセットを全て用いて、その変数群を合成して代表できる変数を作成することでした。これに対して、因子分析では独自因子が存在していることを前提に、この要素を省いた形で背後に存在する、原因となっている因子を発見することが目的となります。因子分析の結果は「変数の背後に存在する原因」であり、主成分分析の結果は「変数から導き出された結果」であるというアプローチの違いがあります。また独自因子という誤差を想定するのか、それともそこにあるデータを全て利用するのかという違いが存在します。
一方で、固有値/固有ベクトルを利用して因子、もしくは主成分を導き出すテクニックは共通しており、手法としての近似性、同一部分があるのも事実です。