Teradata Vantage™ - Unbounded Array Frameworkの時系列機能 [リリース日:2022/6 リリースバージョン:17.20]の内容をもとに作成しています。
Vantageアナリティクス シリーズのコンテンツです。
無制限配列フレームワークとは?
主な特徴
- 1次元の系列(シリーズ)と、2次元の行列(マトリックス)を使いメモリ空間を超える大容量データの分析ができます。
- データを時間順序に持つことで、時系列データに対して高速に処理を行う事ができます。
- 時系列分析、デジタル信号処理の関数が用意されています。
- Vantageの他の機械学習機能などと組み合わせて利用することで多様な分析に利用できます。
- データを様々な種類のグラフにプロットして、高速でビジュアライズしたグラフを作成することもできます。
処理イメージ(行列の場合)
無制限配列フレームワークは、通常テーブルから配列にタイムコードもしくはシーケンス順序にデータを読み込み用意された関数で処理を行います。結果はART(分析結果テーブル)に格納されます。
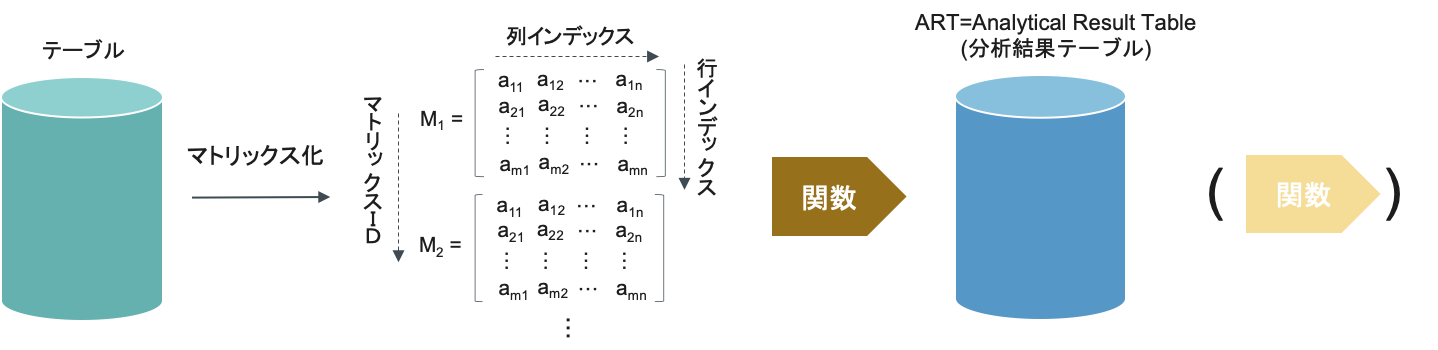
構成要素
| 構成要素 | 説明 |
|---|---|
| 行列(マトリックス) | 行列(マトリックス)とは、行と列を持つ2次元の配列である。行列(マトリックス)は複素数をペイロードとします。 |
| 系列(シリーズ) | 系列(シリーズ)は 1 次元配列です。系列(シリーズ)は 実数のベクトルをペイロードとします。別名、多変量時系列データともいいます。 |
| 関数 | 行列(マトリックス)、系列(シリーズ)のデータに対して、特定の変換・分を行う。 |
| ART(分析結果テーブル) | 関数の実行結果データを格納し、その結果を別のUAF関数に渡せるようにします。通常テーブルと揮発テーブルが選べます。 |
| テーブル | Teradataの物理テーブルです。 |
配列形式
無制限配列フレームワークのデータは、以下2種類の配列形式を利用することが出来ます。
各配列はサポートされている Teradata テーブル タイプ内に格納されます。

タイムシリーズ関数(無制限配列フレームワーク)
タイムシリーズ関数は、新しくリリースされた無制限配列フレームワーク(Unbounded Array Framework=UAF)上で動作し、50以上のインデータベースでのでの時系列分析とデジタル信号処理の関数により、数百万個の製品や数十億個のセンサーなどの時系列データを継続的に予測することが可能です。

各関数の使い方については、Teradata Vantageドキュメンテーションにリンクしていますので、Teradata Vantageドキュメンテーションのマニュアルを参照して、利用方法の確認をお願いします。
ユーティリティ
| 機能 | 説明 |
|---|---|
| シリーズ情報 (TD_SINFO) |
論理系列を説明するメタデータを返します。 |
| マトリックス情報 (TD_MINFO) |
論理行列を説明するメタデータを返します。 |
| 非離散的なデータの調査 (TD_INPUTVALIDATOR) |
データを検証し、系列または行列に渡された非離散的なデータを見つけます。 |
| 結果セットを取得 (TD_EXTRACT_RESULTS) |
分析結果テーブル(ART)に保存されている、セカンダリおよび3次レイヤーなどの補助結果セットを取得します。 |
| データプロット (TD_PLOT) |
オンデマンドのプロットを生成する機能を提供します。生成されるプロットは、本質的に一変量、多変量、または複合のいずれかになります。 |
| テーブル変換 (TD_CONVERTTABLEFORUAF) |
有効なデータ型で構成される入力テーブルを、UAF系列または行列仕様と互換性のあるデータ レイアウトを持つテーブルに変換します。 |
| 地理空間データの計算 (TD_TRACKINGOP) |
旅行の移動距離、速度、時間について地理空間データを計算します。 |
データ準備
| 機能 | 説明 |
|---|---|
| シリーズ四則演算 (TD_BINARYSERIESOP) |
同じサイズの2つの時系列でポイントごとの数学演算を実行します。数学演算は、加算、減算、乗算、または除算です。 |
| マトリックス四則演算 (TD_BINARYMATRIXOP) |
同じ数のウェーブレットを持ち対応するウェーブレットに同じ数のデータ ポイントがある2つの行列に対して、ポイントごとの数学演算を実行します。数学演算は、加算、減算、乗算、または除算です。 |
| シリーズ生成(式から) (TD_GENSERIES4FORMULA) |
式主導の系列を生成します。この目的は、TD_BINARYSERIES_OP減算演算を使用してデータから周期性を除去するための系列を生成することにあります。 |
| シリーズ生成(マトリックスから) (TD_MATRIXMULTIPLY) |
2つの行列に基づいてデータ系列を作成します。 |
| リサンプル (TD_RESAMPLE) |
時系列や空間系列などの論理系列を受け取り、補間アルゴリズムを適用して、ターゲットの開始点とターゲットのサンプリング間隔を持つ離散系列に変換します。 |
診断的記述統計
| 機能 | 説明 |
|---|---|
| Breusch–Godfrey検定 (TD_BREUSCH_GODFREY) |
Breusch–Godfrey検定を使用して回帰により生成された残差を分析します。 |
| Breusch-Pagan検定 (TD_BREUSCH_PAGAN_GODFREY) |
回帰モデルについて分散が等分散かまたは不均一分散かを判別します。 |
| 累積ピリオドグラムの統計検定 (TD_CUMUL_PERIODOGRAM) |
モデリングするデータに最適なモデルを決めるために役立ちます。すべての周期性を同時に検定します。 |
| ディッキー–フラー検定 (TD_DICKEY_FULLER) |
特定の系列生成プロセス内に1つ以上の単位根が存在するかどうかを検定します。 |
| ダービン・ワトソン検定 (TD_DURBIN_WATSON) |
Durbin-Watson検定を使用して、系列またはART回帰により生成された残差を分析します。 |
| モデリング実行の適合度 (TD_FITMETRICS) |
元の系列、予測された系列、元の系列の平均、およびモデリング適合の実施からの残差を使用して、モデリング適合実行における適合度を判定します。 |
| ゴールドフェルド・クォント検定 (TD_GOLDFELD_QUANDT) |
系列サンプル ポイントを2つのサンプル ポイント集合に分割し、分散が等分散か不均一分散かを判定します。 |
| かばん検定 (TD_PORTMAN) |
残差にゼロ平均があるか、系列相関の証拠がないか、または残差が等分散を示しているかどうかを判定します。 |
| 予測モデリング測定基準 (TD_SELECTION_CRITERIA) |
モデル検証実行で残された残差に対して、測定基準を計算します。データ サイエンティストは生成された測定基準を使用して、どの予測モデル候補を使用するかを決めます。 |
| 周期性の有意性統計検定(TD_SIGNIF_PERIODICITIES) | 最適なデータモデルを求めるための周期性統計検定の有意性です。この関数は、予測されたデータ ポイントを使用したモデル検証中に生成された残差を使用します。 |
| 残差平均統計検定 (TD_SIGNIF_RESIDMEAN) |
最適なデータモデルを求めるための残差平均統計検定の有意性です。この関数は、予測されたデータ ポイントを使用したモデル検証中に生成された残差を使用します。 |
| Whites-General検定 (TD_WHITES_GENERAL) |
回帰分析での不均一分散エラーを識別します。これは、Goldfeld-Quandt検定よりも単純な実施方法であり、Breusch-Pagan-Godfrey検定に必要な正規分布にも影響されません。 |
モデル準備とパラメータの推定
| 機能 | 説明 |
|---|---|
| 自己相関 (TD_ACF) |
時系列の自己相関または自己共分散を計算します。 |
| ARMAモデルのパラメータ推定 (TD_ARIMAESTIMATE) |
季節性および非季節的な自己回帰モデル、移動平均モデル、およびARIMAモデルとしての組み合わせARMAモデルのパラメータ推定を実行します。 |
| ARMAモデルの評価メトリック出力 (TD_ARIMAVALIDATE) |
モデル選択の測定基準集を提供します。 |
| 差分時系列変換 (TD_DIFF) |
定常、季節性、または非定常の時系列を、差分時系列に変換します。 |
| 線形回帰関数 (TD_LINEAR_REGR) |
説明変数と応答変数との関係を定義する式を使用して、データを曲線に適合させます。単純な線形回帰関数を使用します。 |
| 多変量線形回帰関数 (TD_MULTIVAR_REGR) |
説明変数と複数の応答変数との関係を定義する式を使用して、データを多次元表面に適合させます。多変量線形回帰関数を使用します。 |
| 偏自己相関 (TD_PACF) |
タイム ラグの影響を取り除いた場合の、時系列サンプル ポイント間の相関度を測定します。 |
| べき乗変換 (TD_POWERTRANSFORM) |
非定常の分散をともなう時系列にべき乗変換を適用し、定常の分散をともなう新しい時系列を作成します。 |
| 季節変動の調整 (TD_SEASONALNORMALIZE) |
データセット内の周期的な季節パターンを正規化します。 |
| 平滑化関数 (TD_SMOOTHMA) |
非定常平均の時系列に平滑化関数を適用し、定常平均の新しい時系列を作成します。 |
| 差分時系列の逆変換 (TD_UNDIFF) |
TD_DIFF関数により作成された差分時系列を再構築します。 |
| 季節変動の非正規化 (TD_UNNORMALIZE) |
TD_SEASONALNORMALIZE関数によって実行された季節的な正規化を逆にします。 |
シリーズ予測機能
| 機能 | 説明 |
|---|---|
| ARIMA予測 (TD_ARIMAFORECAST) |
ARIMAアルゴリズムを使用して、モデルで最後に観測されたサンプル ポイントより先の将来的なユーザー定義の期間数を予測します。この関数は、予測された値を含むプライマリ結果セットのみを出力します。 |
| 動的時間伸縮法 (TD_DTW) |
検索半径に応じて、2つの系列間の最適または最適に近いワープパスを検索します。 |
| ホルト-ウィンターズ法 (TD_HOLT_WINTERS_FORECASTER) |
Holt Wintersモデルを使用して、モデルで最後に観測されたサンプル ポイントより先の将来的なユーザー定義の期間数を予測します。この関数は、4つまでの結果セットを出力します。 |
| 移動平均予測 (TD_MAMEAN) |
利用可能な過去のデータを使用して、将来的なユーザー定義のアクティビティ期間数を予測します。 |
| 単純指数平滑法 (TD_SIMPLEEXP) |
レベルモデリング成分を使用する予測モデルを使用して、元の系列の予測を実行します。 |
時間・空間機能
| 機能 | 説明 |
|---|---|
| 畳み込み (TD_CONVOLVE) |
時系列をカーネルフィルタで畳み込むことにより、デジタル フィルタを1次元系列に適用します。 |
| 2次元の畳み込み (TD_CONVOLVE2) |
時系列をカーネル フィルタで畳み込むことにより、デジタルフィルタを2次元行列に適用します。 |
| 1次元離散高速フーリエ変換 (TD_DFFT) |
離散高速フーリエ変換を1次元系列に適用し、計算されたフーリエ係数を含む結果系列を返します。係数は、長方形(実数、虚数)の形式または極(振幅、位相)形式にできます。 |
| 2次元離散高速 |
|
| フーリエ変換 (TD_DFFT2) |
離散高速フーリエ変換を2次元配列に適用し、計算された2次元フーリエ係数を含む結果行列を返します。係数は、長方形(実数、虚数)の形式または極(振幅、位相)形式にできます。 |
| 1次元高速フーリエ変換コンバータ (TD_DFFTCONV) |
TD_DFFTによって生成されたフーリエ係数結果系列(ART)を、人間に判読可能な形式またはraw形式に、サポートされる任意の長方形および極出力形式で変換します。 |
| 2次元高速フーリエ変換コンバータ (TD_DFFT2CONV) |
TD_DFFT2により生成されるフーリエ係数結果行列(ART)を、人間に判読可能な形式またはraw形式に、サポートされる任意の長方形および極出力形式で変換します。 |
| 正弦波生成 (TD_GENSERIES4SINUSOIDS) |
元の入力系列の正弦波要素のサブセットを含む結果系列を生成します。 |
| 1次元逆離散フーリエ変換 (TD_IDFFT) |
1次元系列に対するフーリエ変換の効果を逆にします。 |
| 2次元逆離散フーリエ変換 (TD_IDFFT2) |
2次元行列に対するフーリエ変換の効果を逆にします。 |
| 線スペクトル (TD_LINESPEC) |
時系列の周期性を識別するためにライン スペクトル関数を使用します。 |
| パワースペクトル (TD_POWERSPEC) |
時系列に関連付けられたパワースペクトルを推定するためにパワースペクトル関数を使用します。 |
警告
この本書はTeradata Vantageドキュメンテーションよりトピックに必要な情報を抜粋したものです。掲載内容の正確性・完全性・信頼性・最新性を保証するものではございません。正確な内容については、原本をご参照下さい。
また、修正が必要な箇所や、ご要望についてはコメントをよろしくお願いします。