この本書は2017年4月1日にTeradata Japanのブログに掲載された内容を、再掲載したものです。
掲載内容の正確性・完全性・信頼性・最新性を保証するものではございません。
また、修正が必要な箇所や、ご要望についてはコメントをよろしくお願いします。
著者 山本 泰史 (やまもと やすし)
顧客分析の手順
第7回: 2つ以上の変数を組み合わせる
単一の変数それぞれに関する理解が得られた段階で、次に実施するべきは、2つ以上の複数変数間の関係を見定めます。今回はまず 2つの変数間の関係を把握する方法について理解し、続いて 2つ以上の変数間の関係について考察します。
散布図
2変数の関係を視覚的に把握するための簡単な方法は、散布図によるグラフ表現です。図11 では、2つの変数を縦横に配置し、それによって説明される各顧客を点としてプロットしています。これによって 2変数間の関係について把握することが可能です。相関関係のある変数であれば、プロットされた点に一定の法則が見られます。例えば正比例の関係、反比例の関係はこの相関関係の代表的なものです。また、特定のいくつかのグループに分かれていることを発見できる場合もあります。

相関係数
前述した正比例、反比例の関係への当てはまり具合を示してくれる指標が、相関係数です。相関係数の数式、算出方法は冗長かつ脱線になるため割愛しますが(乱暴な説明で済ますと、2変数の共分散を各変数の標準偏差で割って算出します。詳しくお知りになりたい方は、統計関連の書籍や Webサイト等の解説をご覧になることをお勧めします)、スプレッドシートや各種分析ツールでその算出機能が実装されており、それらを用いることが可能です。
相関係数は -1 から 1 の値をとり、-1 に近ければ近いほど両変数は反比例の関係に有り、1 に近ければ近いほど正比例の関係にあります。そして 0 に近ければ近いほど相関関係は低いということになります。図12 はこのような関係を図示したものです。
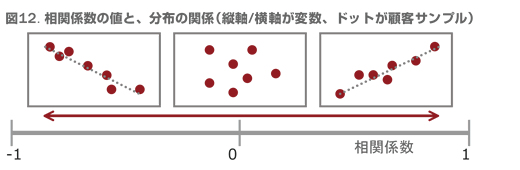
2つの変数間で何らかの関係が見出せる場合、「どちらかがもう片方に影響を与えているかもしれない」という仮説が成り立ちます。これは何らかの原因を追究していく上で、参考になる傾向です。
3変数以上の場合: データマイニング
2変数の場合、お互いが比較の対象となるため、比較的把握が容易なのですが、コトが 3変数以上になった場合、事態はちょっと難しくなります。図13 は 3変数を利用してそれぞれの顧客をプロットしたチャートです。Teradata Warehouse Miner という当社のデータマイニング・ツールを利用して作成しました。3変数までであればこのように立体空間として表現可能ですが、それ以上になると分かりやすく把握するには限界があります。おそらく、図13 でさえ、2変数に比べると分かりづらく、このチャートのように色々な角度から見ればなんとなく傾向が掴めるという程度ではないでしょうか。
図13. 3変数の散布図(赤いドットが顧客、利用変数は利息合計、口座残高、元本)
3変数以上の関係を理解する場合、一つの方法はデータマイニングの手法を利用することです。データマイニングの分析手法はいくつかありますが、単純化すれば、図14 のような変数を新たに作り出し、得られた変数を単一の変数として理解します(単一の変数になった後の分析は、前回ご紹介したとおりです)。図14 には確率値、分類値、定量値と 3つの変数が得られています。確率値を得るのにはロジスティック回帰分析、もしくはデシジョンツリー分析が利用されるのが一般的です。また分類値にはクラスター分析(2値への分類 = 分岐にはデシジョンツリー分析も利用可能)、そして定量値には線形回帰分析や因子分析等が用いられます。

補足として確率値を算出する場合のメカニズムを簡単に示します。特定の 0 もしくは 1 で示される変数(例: 解約結果)を「結果変数」として利用し、他の変数群を「説明変数」として利用することによって、確率値(例: 解約確率)を算出します。確率値は 0 から 1 の間で示されますが、「結果変数として利用される変数は、他の説明変数によって説明できる」という前提に立ち、他の説明変数群を組み合わせて結果変数の傾向にそった確率値を算出します。このような関係から、説明変数を「独立変数」、結果変数を「従属変数」とも呼びます。これは説明変数がそれぞれに独立して発生した変数であること、そしてそのそれぞれに独立した変数によって結果変数が導き出されたと仮定していることから来ている言葉です。その他の詳細に関しては別稿「マーケターのためのデータマイニング・ヒッチハイクガイド」を参照いただきたく、詳細は割愛します。
3変数以上の場合: 多次元分析
3変数以上の関係を理解する場合のもう一つの方法は顧客の側、つまり行を集約してしまうことです。図15 は、これまで顧客番号として配置していた行を、性別で分割し、その上で集約しています。これによって行側がシンプルに表され、性別での違いを各変数間で把握することが可能となります。この場合、各変数は性別ごとに代表値で集約(平均、合計等)される必要があります。また、行を集約する際に利用した変数(ここでは性別)を変数として利用することができません。ここでは性別ごとに分割、集約していますが、これ以外の顧客属性、指標、商品やサービス、チャネル等で分割、集約する場合も考え方は同じです。
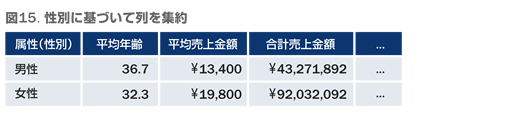
このように行を特定変数に基づいて分割/集約することを、一般にセグメンテーションと呼びます。いくつかのセグメントに分類することによって、変数の偏りや傾向がより明確になる可能性を有しています。また複数のセグメント間で比較することによって、顧客の類型が出来上がり、これによって異なるニーズが明快になり、案内オファーを個別化する際の重要な情報として活用できるかもしれません。次回は、このようなセグメント作成の考え方についてご紹介します。