本書は2017年4月1日にTeradata Japanのブログに掲載された内容を、再掲載したものです。
掲載内容の正確性・完全性・信頼性・最新性を保証するものではございません。
また、修正が必要な箇所や、ご要望についてはコメントをよろしくお願いします。
著者 山本 泰史 (やまもと やすし)
決定木
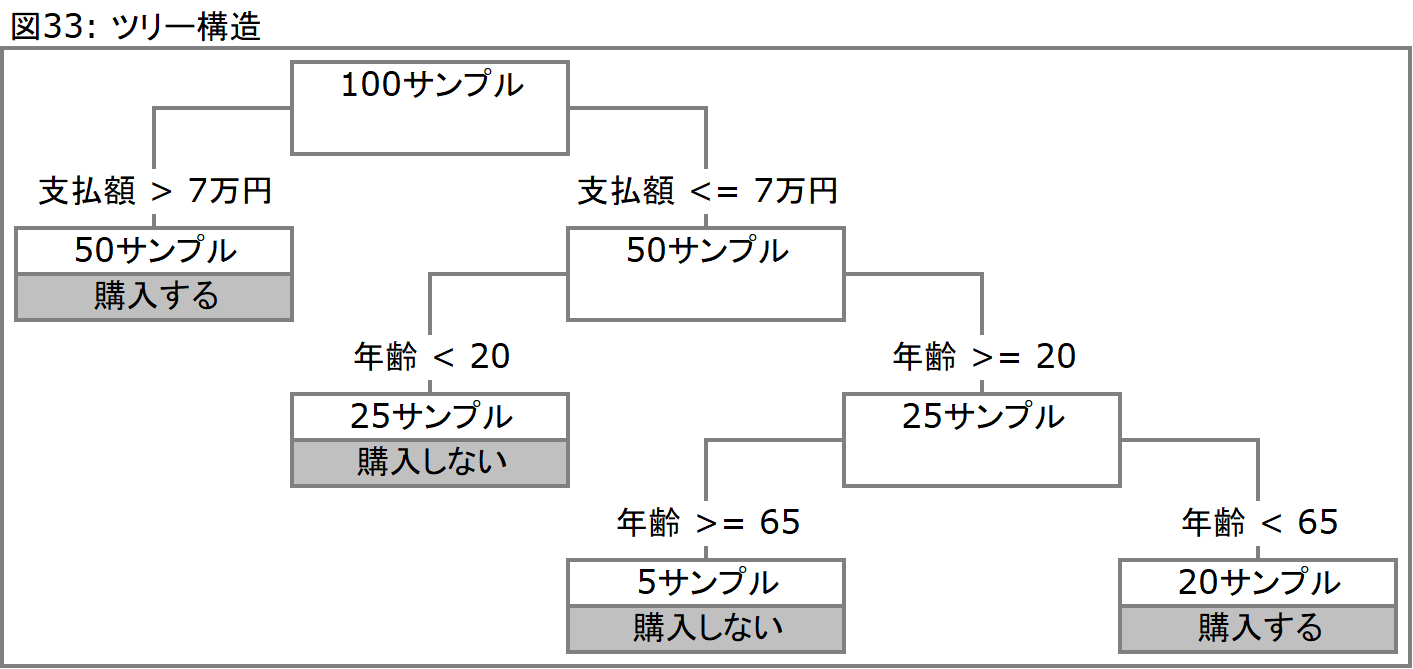
この手法は意思決定ツリー、またはデシジョンツリーとも呼ばれる手法で、樹形図、またはツリー構造と呼ばれる図を作り出し、アウトプットには分類を行なうためのルールを作成します。決定木を実施した場合、アウトプットとして以下図33のようなツリー構造が示されます。ここで、このツリー構造は、ノード(節)と、そこから分岐したリーフ(葉)で示されます。ノードはそこからの分岐条件を示し、データサンプル(ここでは顧客)は次のノード、もしくはリーフへと引き渡されます。リーフはこれ以上分岐する必要がない状態を意味し、最終的な分類を意味します。これを別な形で表現すると、図34のようなIF THEN形式のルールになります。
決定木は、上述した例のように予測(購入するグループと、しないグループ)に活用することも可能ですし、この構造を利用して分類に活用することも可能です。クラスター分析は分類の分岐条件を提示しないため、人間がそれを解釈しなければならないのに対して、決定木はこのようなIF THEN形式によって分類の分岐条件を説明してくれます。そのため、分類に対する理解を得やすいという性質があります。しかしながらクラスター分析で紹介したような傾きのある直線で分岐を行なう形式ではないため、分岐そのものの鋭さという意味ではクラスター分析が勝っています。

■利用するデータセット
図35をご覧頂きたいのですが、縦軸に顧客をリストアップし、説明変数として年齢、住居区分、そして住宅ローン購入(申し込み)有無に関するデータをデータセットとして用意しています。ここでの命題は、年齢、住居区分を用いて住宅ローン購入の有無を説明することです。本来はもっと多くの変数を用いることになるはずですが、ここでは手法について紹介することが目的であるため、若干乱暴であることは承知の上でこの2変数のみを利用します。尚、各データ値にはアルファベット(M)とその意味合い(男性)が表示されていますが、実際にデータ値として利用されるのは数値(0 or 1)データです。補足と以降の説明のため、以下のように記載しています。以降各データ値は、例えば男性であればMで説明をしていきます。また住居区分は、住宅ローンを組む前のステータスデータです。従って、比較的若い方で親元に暮らしている方の場合、その家が持家であれば、「持家」と区分されます。同様にその住居が賃貸であれば「借家」となります。もちろんその本人が世帯主となっている住居について分類されている場合もあります。
住宅ローンの購入データは、被説明変数として利用されるデータであり、言わば結果のデータです。この結果つきのデータを用いてルールを構築します。スコアリングにおいてはこのルールを用いますが、当然ながら購入データは存在せず、これが予測の対象となります。与えられた変数のみで住宅ローンの購入有無を説明、予測できれば、住宅ローンを販売するべき顧客群を特定することが可能となります。「住宅購入顧客を決定付ける条件(変数とその分岐)は何か?」ということがここでの答えになるのです。

決定木を作り出す上で実施される分類手法、分類の基準には、主にジニ係数(CART)、もしくはエントロピー(C4.5)のいずれかが用いられます。ここではそのそれぞれについて、簡単に紹介します。
■ジニ係数(CART)
データマイニングの世界ではCARTとして、計量経済学(マクロ経済の計量的把握を目的とした経済学)の分野ではジニ係数として知られるアルゴリズムをここでは利用します。ジニ係数は本来、社会における所得分配の均衡、不均衡を表すために用いられている尺度であり、0から1の値をとり、0に近いほど平等な社会であるとされ、逆に1に近いほど格差が大きく、不平等(高所得者への所得集中)な社会であるとされています(例えばブラジルのジニ係数は0.6を越えます。一方で日本のジニ係数は大体0.3から0.4の間にありましたが、90年代以降上昇傾向にあり、0.5に近い数値に推移しています)。データマイニングにおいて、ジニ係数の0は値の純粋さ(Pureness)を意味し、これ以上分割できない状態を意味します。一方で分類前のデータは比較的1に近い状態にあり、ジニ係数を1から0へと近づけていくように分類していくことが、決定木における分類の考え方です。
決定木においては、既に求めたい結果が分かっているデータを利用して分類モデルを作成していきます。例えば、「ある商品を購入するか否か」を最もよく説明してくれる分類を作成したとき、既に当該商品を購入した顧客のデータ、そして購入しなかった顧客のデータが用いられます。つまり利用すべき変数の1つに[商品購入 : Yes / No]のデータが存在しており、このYesとNoをきれいに選り分けてくれる説明変数と、それに適用する分岐条件を探し出すことが目的となります。ちなみに上述した値の純粋さとは、究極的に分類されたデータが全てYesの値をとる、もしくは全てNoの値をとることです。従って最初のノードにある全てのデータの不純さ(Impureness)を、分割することによって純化していく作業であるとも言えます。(デリカシーがない表現なのは承知の上で)ブラジルのジニ係数に喩えるのであれば、所得の高い人と、所得の低い人に人口を分割して2つの国を作ることによって、それぞれの国のジニ係数を低下させると考えていただくと理解しやすいのではないかと思います。
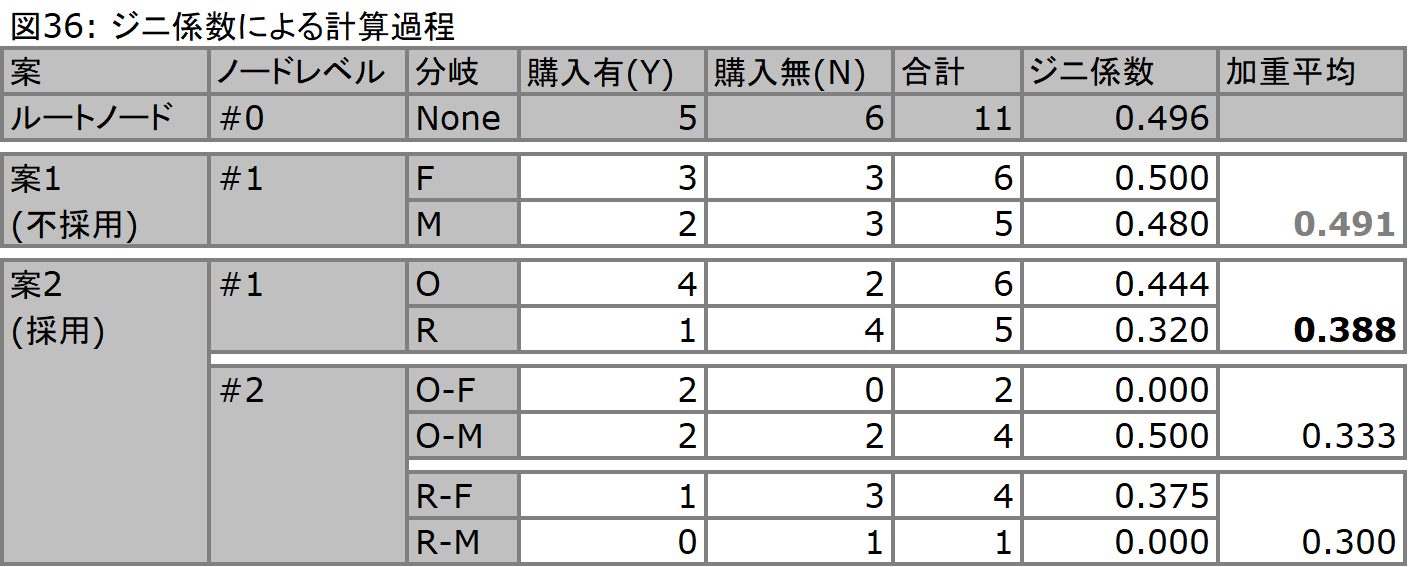
さて、ここで購入を説明するデータセットとして図35を考え、これに基づいた処理の流れを以下の図36で例示することにします。このケースにおいて利用できる変数は2つのみであり、とりうるパターンはどちらの分岐を上のノードに持ってくるかだけです。従って、アルゴリズムがそうするように、この2つのパターンをそれぞれに計算して、吟味することにします。当然ながらコンピューター上で実施されるアルゴリズムはこのような計算を、多くの変数を用いて実施することになりますし、またそれぞれの変数における分岐もこのケースに見られるようなオン/オフの分岐だけではありません。ただし、このアルゴリズムを用いる場合の分岐数は必ず2つになります。
データマイニングにおいてジニ係数は、確率的な考え方をベースに構築されます。図36のノード#0では、最初のノードのジニ係数を計算していますが、これはYesを発生確率、Noを発生しない確率と見立てた場合の、それぞれの2乗を1から引いて得られたものです。あるノード(どこでも良いのですがノード#0とします)に含まれるレコード群を考えます。ここではそれぞれがYもしくはNの値を必ず持っており、このノードから1つのデータサンプルをピックアップしたときのYが出る確率と、Nが出る確率はそれぞれ5/11と6/11となることを意味しています。また、ここでこのピックアップを2回実施したとき、その組み合わせは、{YY, YN, NY, NN}となります。例えばYYの同時発生確率は、(5/11)*(5/11) = (5/11)2で表されます。そしてこのいずれかが発生するため、確率の総和 = YY + YN + NY + NN = 1が成り立ちます。ジニ係数とは不純さを示す尺度として用いられるため、ここでジニ係数はYN + NYで求められ、左辺にYN + NY、右辺に1 - (YY + NN)を置いて、YN + NY = 1 - (YY + NN)となります。言い換えると、右辺は不純である確率の合計であり、左辺は1から純粋である確率を差し引いた値であり、両辺は等しい関係にあります。そしてここで右辺は1 - ((5/11)2 + (6/11)2)となり、これがジニ係数です(図36内0.496)。
ここでノード#0では、Yesが5、Noが6となっているため、確率的には不純であり、よってジニ係数も0.496という数値になっています。まずこれを性別に基づいて分類することにします(案1)。女性に分岐した方は、購入=3、未購入=3となっており、不純なままです。単独のジニ係数を見ると係数が逆に上昇していることが分かります。男性に分岐した方は、購入者数 = 2、未購入者数 = 3となり、あまり不純さは変わりそうにありません。単独のジニ係数では0.480となっています。ここではこのノードレベルでのジニ係数を理解したいため、加重平均を取ると、案1におけるジニ係数の加重平均は、0.491となり、さほどジニ係数を低下させていないようです。
これに対して案2を見た場合、住居区分は購入/未購入の別を説明するのにより良い変数であることが想定されます。同様の計算を施すと、それぞれのジニ係数が、0.444、0.320となり、加重平均は0.388となります。よって最初に分類として利用するべきは、住居区分であることが分かり、案2が採用されます。
さらにこの下のノードレベル(ノード#2)で、性別に基づいて分岐を重ねていくことにします。ここで注目していただきたいのは、持家女性(O-F)の分岐と、借家男性(R-M)の分岐です。ジニ係数が0となっており、これ以上ない均質さ(YesもしくはNoのどちらかで独占されている状態)を有していることが分かります。ここまで進むと分岐は終了します。ただし、借家男性(R-M)の分岐に属するデータが1件しかないというのはちょっと心もとないものです。元々のデータサンプルが11件しかないため無理もないのですが、実際には膨大な件数のデータを用いる際にもこのようなことは発生します。当然ながらジニ係数 = 0に向かって分岐を繰り返していくため、最終的に枝葉のレベルではこのような小さなサンプルに基づいたルールが発生することになるのです。そのため、実際にはこのモデル作成に利用したデータとは別のデータにこのモデルを適用させることによって、エラーの発生率を把握し、実際に有意なノードを残して、有意でないノードを刈り取ることになります。「有意でないノードを刈り取る」とはつまり、与えられたデータに特有の傾向、しかも枝葉末節に至る傾向をモデルとして取り込んでしまっていて、一般的なデータに対して適用できない部分を削除することです。これによってモデルの適用性を高めることが可能となります(このプロセスは枝刈り、またはプルーニングと呼ばれます)。
■エントロピー(C4.5)
エントロピーという言葉は元々、物理学において用いられていた言葉であり、一般には熱や物質の拡散を表す指標として用いられているものです。一方で情報科学分野では、情報「量」を測るための重要概念としてエントロピーが定義付けられています。ここで説明するのは後者となりますが、両者間に学問的な共通性はないようです(単なる筆者の無学かもしれませんが)。エントロピーとジニ係数で大きく違う点は、必ずしも分岐が2つに限らないという点です。この例では、各変数が2値しかとらないため、分岐は2と変わりませんが、変数のとる値が例えば3つや5つになるとき、それを加味して適切な分岐を作成してくれることになります。一方でこのような分岐の場合、構造は複雑になり、横に広がることになります。
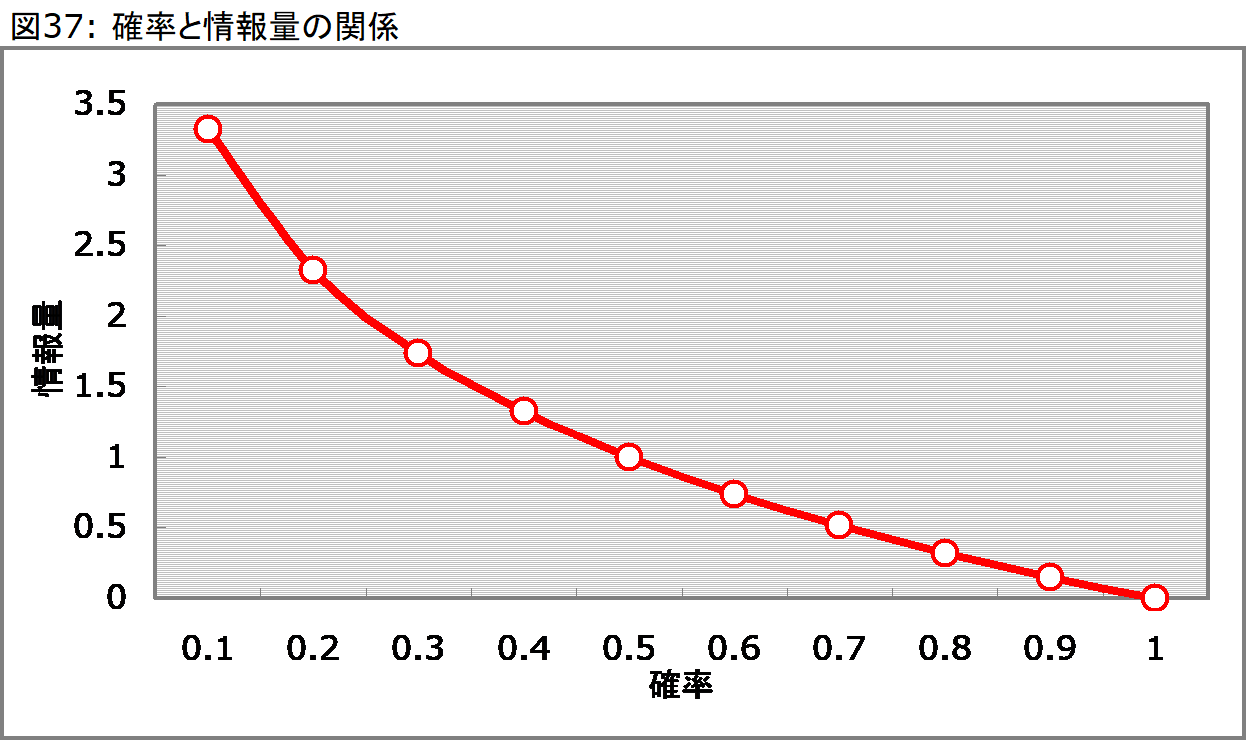
エントロピーの大きな流れはジニ係数で紹介したプロセスと同じですが、ここでジニ係数の代わりに用いられる指標は情報量と呼ばれる指標です。例えば、コインの表裏のような1/2の確率で発生する事象において、コインを投げた結果がわかるとき、その情報量は1と表現されます。また、52枚のトランプからハートを引く確率は1/4(=13/52)ですが、この場合の情報量は2となります。また、コインが表裏のいずれかになる確率は1(=2/2)ですが、この場合の情報量は0となります。ここで確率として表現したことは、得られる結果によって減少する不確実さを意味します。そしてこの2つの間には、上記のような関係が存在し、この情報量の差が分類における判断基準となります。そして、情報量と減少する不確実さ(=確率)の関係は、対数(log)で説明されます(情報量 = -log2確率)。
確率が0に漸近するにつれて、情報量は無限に大きな値(∞)をとりますが、対数関数のグラフなので0へは行き着きません。
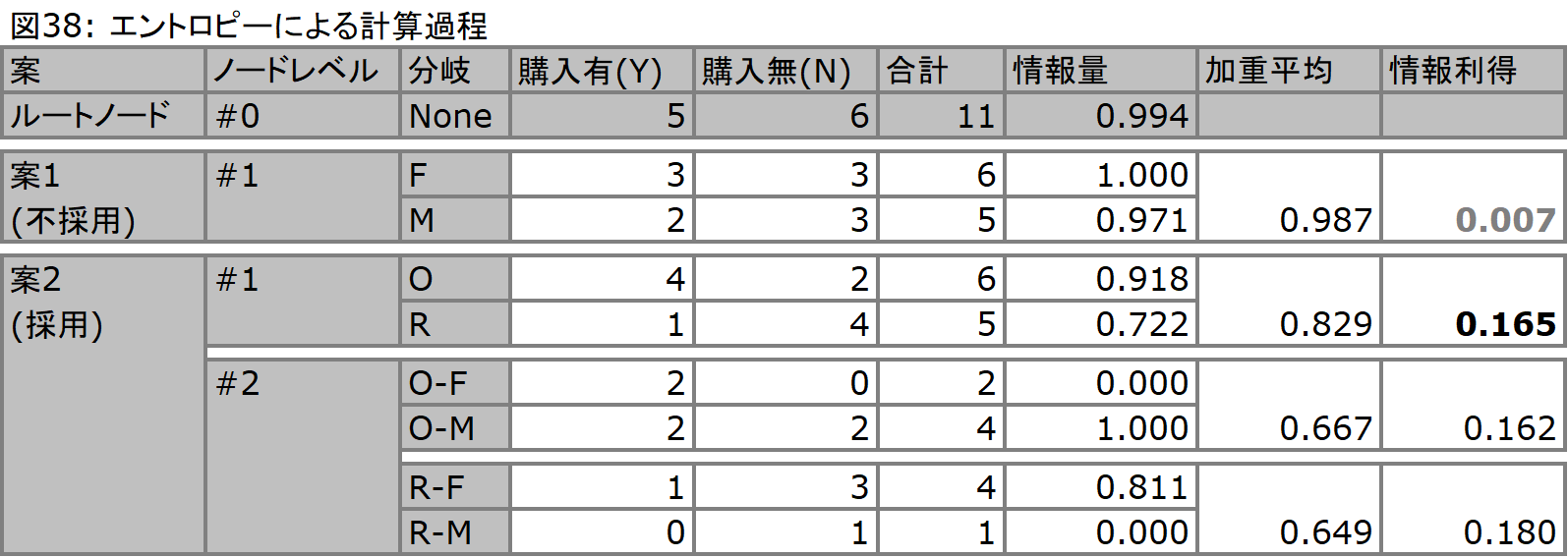
以下の図38では、ジニ係数と同じデータセット(図35)を利用した場合の情報量を算出し、さらにジニ係数の計算同様、加重平均(平均情報量、これをエントロピーと呼びます)を算出しています。また、分岐に用いる判断としては、分岐前のノードと、分岐後のノードの情報量の差(情報利得: Information Gain)をとり、この値の大きい分類を採用しています。ジニ係数と比較した場合、ノード#0のジニ係数が0.5に限りなく近い値を算出していたのに対して、情報量では1に限りなく近い(確率でいうところの0.5に近い)値を算出しているのがお分かりいただけると思います。
情報量は、-(発生確率)*log2(発生確率) -(非発生確率)*log2(非発生確率)で算出されます。ノード#0における計算の場合では、-(5/11)*log2(5/11) -(6/11)*log2(6/11) = 0.994となります。
■ルールの構築
計算過程は、これ以上の分岐が出来なくなるまで続けることが可能ですが、ある一定の分岐回数や、ジニ係数/情報量等に対するトラップを設定して、トラップを下回った段階で計算を終了させることも可能です。また、ルール構築においてもこのトラップを利用します。仮に情報量に対してトラップを設定し、トラップを0.8であるとすると、上述した図38では、ノード#1のR(借家)は分岐が0.8を下回り(0.722)、分岐が終了します。従って、その下で構築されるはずのノード#2のR-FとR-Mは計算されません。一方でノード#1のO(持家)に関しては分岐が続けられ、これがノード#2のO-FとO-Mになります。O-Fに関しては完全な純粋に近い形で分岐が終了します(0.000...)。一方でO-Mに関しては相変わらず不純なまま(1.000)ですが、もはや他には分岐に利用できる変数は存在しないため、これで完了です。以上の結果を用いた場合、構築されるルールは以下の図39のようになります。O-Mにおける購入有/無の比率は2:2であり、確率的には0.5あるのですが、ここでは「購入無し」と判定されます。O-Fとの比較で判断がなされるからです。
以上のデータから判断するに、「持家-女性顧客の方が住宅ローンを購入する(可能性が高い)」という、若干不思議なルールが導き出されますが、最初に用意したデータセットが意図的に作成したものであるため、直感的理解とは合致しなくとも構いません。持家の女性が2名しかおらず、この2名がたまたま住宅ローンを購入した結果は極めて純度の高いものであり、決定木はこの結果を高く評価しています。また、確率上では持家顧客の購入確率が4/6であり、借家顧客の非購入確率は4/5となっており、住居区分を最初に分岐としたという判断も納得がいくものです。
