ICARモデルのMCMCをPyMC5とStanで実行する

PythonでICARモデルが扱いやすくなってきたのでのICARモデルの実装方法を検証してみました。

ここでICARモデルについて詳しい説明はしませんが、一言でまとめると「空間的な相関関係を考慮に入れることができるモデル」になります。ICARモデルについて詳しく知りたい方は下で示しているStanのケーススタディや緑本（データ解析のための統計モデリング入門）をお読みください。

実行環境

今回はGoogleColaboratory（2023年12月1日のバージョン）で検証しました。

使用したPPLは

• PyMC5 (5.10.0)
• Stan (CmdStanPy)

になります。

2023年12月1日現在、GoogleColaboratoryにプリインストールされているPyMC5はバージョンが5.7.2なのでこれを最新版の5.10.0にアップデートして使用しています。

PyMC5の場合は公式がICARモデルを実装してくれているのでそれを使用します。

Stanの場合は正式な実装はありませんが、公式のケーススタディで実装方法を解説してくれているのでこの方法で試します。また、ICARモデルについての詳細な解説がついていますので興味がある方はご一読ください。

使用データ

通称緑本と呼ばれる「データ解析のための統計モデリング入門」の11章で使用されているデータを使用させていただきます。データの詳細については緑本の11章をご確認ください。

実装の下準備

使用したプログラムはこちらに保存していますので必要であれば合わせてご確認ください。

実行環境の整備

まず、GoogleColaboratoryの実行環境を整備します。
以下ではライブラリのインストールと使用するデータのダウンロードを行っています。

# stanの準備
!pip install cmdstanpy
import cmdstanpy
cmdstanpy.install_cmdstan()

# pymcのアップデート
!pip install pymc -U # 5.7.2にはICARがないので5.10.0にアップデート

# 緑本のデータをダウンロード・展開
!wget https://kuboweb.github.io/-kubo/stat/iwanamibook/kubobook_2012.zip
!unzip kubobook_2012.zip

ライブラリのインポート

以下では全体で共通して使用するライブラリのインポートと環境設定を行っています。

import numpy as np
import matplotlib.pyplot as plt
import arviz as az
az.style.use("arviz-white")
import pandas as pd
pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)

データの準備

緑本のデータはRData形式になっているのでここではrpy2を使用してデータを読み込んでいます。

# RDataからデータの取り出し
import rpy2.robjects as ro
ro.r("load('/content/kubobook_2012/spatial/Y.RData')")

# RのベクトルをNumPyアレイに変換
Y_data = np.array(ro.r('Y')) # データ
m_data = np.array(ro.r('m')) # 真の値

注意
GoogleColaboratory上ではrpy2とPyMC5の相性が悪いらしく、一回でもrpy2を読み込むとPyMC5のサンプリング終了時に以下のエラーが出てGoogleColaboratoryがクラッシュしまいました。

WARNING:rpy2.rinterface_lib.callbacks:R[write to console]: Error: ignoring SIGPIPE signal

そのため、実際に使用したコードではY_dataとm_dataをベタ書きで宣言しています。CmdStanPyではこの問題は起きません。

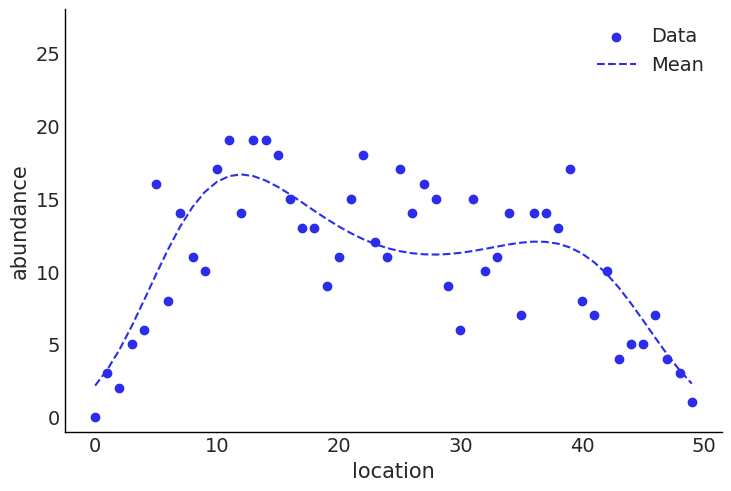
データを図示してみると以下のようになっています。

fig,ax = plt.subplots()
ax.scatter(np.arange(50),Y_data,label='Data')
ax.plot(m_data,linestyle='dashed',label='Mean')
ax.set_ylim(-1,28)
ax.set_xlabel('location')
ax.set_ylabel('abundance')
ax.legend()
plt.show()

locationが隣接しているデータは割と近い値になっています。

隣接行列の準備

今回は隣接しているlcation間では空間的相関関係があるという仮定でモデルを組むために隣接関係を表す隣接行列を準備します。

adj_matrix = np.diagflat(np.full(len(Y_data)-1,1), k=1) + np.diagflat(np.full(len(Y_data)-1,1), k=-1)

adj_matrixは50×50の以下のような配列になります。

[[0 1 0 ... 0 0 0]
 [1 0 1 ... 0 0 0]
 [0 1 0 ... 0 0 0]
 ...
 [0 0 0 ... 0 1 0]
 [0 0 0 ... 1 0 1]
 [0 0 0 ... 0 1 0]]

簡単に解説すると位置(0, 1)は1になっているのでlocation0とlocation1は隣接していることを表しています。一方で位置(0, 2)は0になっているのでlocation0とlocation2は隣接していないことを表しています。

PyMC5でMCMC

ここまででPyMC5でMCMCを実行するのに必要なデータがそろったのPyMC5で実装したいと思います。

モデリング

緑本のモデルをPyMC5で記述すると以下のようになります。

import pymc as pm
import pytensor.tensor as pt
import pytensor

# モデリング
class ICAR_Model(pm.Model):
    def __init__(self, Y, location, adj_matrix):
        super().__init__()

        # 次元
        self.add_coord('location', location)

        # モデル
        beta = pm.Normal('beta', mu=0, sigma=10)
        sigma_phi = pm.Uniform('sigma_phi', lower=0, upper=100)
        phi = pm.ICAR('phi', W=adj_matrix, sigma=1, dims='location') # ICARモデル
        mu = pm.Deterministic('mu', pt.exp(beta+phi*sigma_phi), dims='location')
        obs = pm.Poisson('obs', mu=mu, observed=Y, dims='location')

以下の部分がPyMC5でのICARモデルの書き方です。Wに先ほど準備した隣接行列を指定してsigmaに標準偏差を指定します(ここでは1)。すると（表現が正しいかわかりませんが）標準正規分布のような形の地域差をモデリングできます。

phi = pm.ICAR('phi', W=adj_matrix, sigma=1, dims='location') # ICARモデル

そして、以下のように記述すると地域毎の期待値が得られます。

mu = pm.Deterministic('mu', pt.exp(beta+phi*sigma_phi), dims='location')

以下のように標準偏差のパラメータをICAR()の中で指定してしまう方法もありますが、今回のモデルでは収束が非常に悪くなりました。

phi = pm.ICAR('phi', W=adj_matrix, sigma=sigma_phi, dims='location') # ICARモデル
mu = pm.Deterministic('mu', pt.exp(beta+phi), dims='location')

標準偏差のパラメータを確率分布の外に出してしまう方法を再パラメータ化と言い、収束が悪いときに有効な方法の一つです。再パラメータ化については以下の記事が非常にわかりやすくまとめてくれています。

モデルをグラフィカルモデルにしてみます。

model = ICAR_Model(Y=Y_data, location=np.arange(Y_data.shape[0]), adj_matrix=adj_matrix)
pm.model_to_graphviz(model)

MCMCを実行します。

idata_pymc = pm.sample(
    draws=1000,
    tune=1000,
    chains=4,
    random_seed=0,
    cores=4,
    model=model
)

MCMCのみで8分49秒、コンパイル等を含むと9分40秒かかりました。

結果の確認

display(az.summary(idata_pymc))

これを実行すると各パラメータの要約統計量やESS(ess_bulk, ess_tail)、r-hatなどが表示されます。r-hatは全て1.0で、最も低いessも500以上あるので問題なさそうです。長い表になるのでここに記載するのは省略します。

以下でトレースプロットも確認しておきます。

az.plot_trace(idata_pymc.posterior)

こちらも問題はなさそうです。

最後にデータと推定値を一緒に図示してみます。

# HDIの95％信用区間
pymc_hdi=az.hdi(idata_pymc.posterior['mu'],hdi_prob=0.95)
# 中央値の計算
pymc_median = np.median(idata_pymc.posterior['mu'],axis=(0,1))

# 結果の図示
fig,ax = plt.subplots()
ax.fill_between(np.arange(50),pymc_hdi.mu[:,1],pymc_hdi.mu[:,0],color='lightgray',label='95%HDI (PyMC5)')
ax.plot(pymc_median,color='black',label='Median (PyMC5)')
ax.scatter(np.arange(50),Y_data,label='Data')
ax.plot(m_data,linestyle='dashed',label='Mean')
ax.set_ylim(-1,28)
ax.set_xlabel('location')
ax.set_ylabel('abundance')
ax.legend()
plt.show()

グレーが95%信用区間、黒線が中央値、青が元データです。緑本の図とほぼ同じ図になりました。

StanでMCMC

今度はCmdStanPyで実装したいと思います。

隣接行列のベクトル化

Stanでは隣接行列を1次元のベクトルとして扱うために少し加工します。

_node1, _node2 = np.where(adj_matrix==1)
node1 = _node1+1 # 要素番号0がstanでは使えないため＋1しておく
node2 = _node2+1

node1は以下のように

[ 1  2  2  3  3  4  4  5  5  6  6  7  7  8  8  9  9 10 10 11 11 12 12 13
 13 14 14 15 15 16 16 17 17 18 18 19 19 20 20 21 21 22 22 23 23 24 24 25
 25 26 26 27 27 28 28 29 29 30 30 31 31 32 32 33 33 34 34 35 35 36 36 37
 37 38 38 39 39 40 40 41 41 42 42 43 43 44 44 45 45 46 46 47 47 48 48 49
 49 50]

node2は以下のように

[ 2  1  3  2  4  3  5  4  6  5  7  6  8  7  9  8 10  9 11 10 12 11 13 12
 14 13 15 14 16 15 17 16 18 17 19 18 20 19 21 20 22 21 23 22 24 23 25 24
 26 25 27 26 28 27 29 28 30 29 31 30 32 31 33 32 34 33 35 34 36 35 37 36
 38 37 39 38 40 39 41 40 42 41 43 42 44 43 45 44 46 45 47 46 48 47 49 48
 50 49]

なります。

各隣接するlocation間の総当たりをforループではなくベクトルとして行うためにこのようにしています。

モデリング

緑本のモデルをStanで記述すると以下のようになります。ここではStanファイルの生成までを行っています。

stancode = """
data {
    int<lower=0> n_locaition;
    int<lower=0> n_edge;
    array[n_edge] int<lower=1, upper=n_locaition> node1;
    array[n_edge] int<lower=1, upper=n_locaition> node2;
    array[n_locaition] int<lower=0> Y;
}

parameters {
    vector[n_locaition] phi;
    real<lower=0> sigma_phi;
    real beta;
}

transformed parameters {
    vector[n_locaition] mu = exp(beta + phi*sigma_phi);
}

model {
    // ICARここから
    target += -0.5 * dot_self(phi[node1] - phi[node2]);
    sum(phi) ~ normal(0, 0.01 * n_locaition);
    // ICARここまで

    beta ~ normal(0, 10);
    sigma_phi ~ uniform(0, 100);
    Y ~ poisson(mu);
}
"""
with open('model.stan','w') as f:
  f.write(stancode)

以下の部分がStanでのICARモデルの書き方です。なぜ、このような形になるのかは公式のケーススタディに書かれていますので詳細はそちらを参照してください。

target += -0.5 * dot_self(phi[node1] - phi[node2]);
sum(phi) ~ normal(0, 0.01 * n_locaition);

MCMCを実行します。PyMCと同じくサンプルをArvizで扱うために最後に変換しています。

from cmdstanpy import CmdStanModel

# MCMCの実行
model = CmdStanModel(stan_file=f'/content/model.stan')
fit = model.sample(
    data={
        'n_locaition':Y_data.shape[0],
        'n_edge':node1.shape[0],
        'node1':node1,
        'node2':node2,
        'Y':Y_data.astype(int)
    },
    chains=4,
    iter_warmup=1000,
    iter_sampling=1000,
    seed=1,
)
# xdarray形式にサンプルを変換
idata = az.InferenceData(posterior=fit.draws_xr())

MCMCのみで1秒、コンパイル等を含むと45秒でした。めちゃくちゃ速いです。

結果の確認

display(az.summary(idata))

Stanではr-hatは1.00～1.01で、最も低いessで500以上なので問題なさそうです。

以下でトレースプロットも確認しておきます。

az.plot_trace(idata_pymc.posterior)

最後にデータと推定値を一緒に図示してみます。

# HDIの95％信用区間
stan_hdi=az.hdi(idata.posterior['mu'],hdi_prob=0.95)
# 中央値の計算
stan_median = np.median(idata.posterior['mu'],axis=(0,1))

# 結果の図示
fig,ax = plt.subplots()
ax.fill_between(np.arange(50),stan_hdi.mu[:,1],stan_hdi.mu[:,0],color='lightgray',label='95%HDI (Stan)')
ax.plot(stan_median,color='black',label='Median (Stan)')
ax.scatter(np.arange(50),Y_data,label='Data')
ax.plot(m_data,linestyle='dashed',label='Mean')
ax.set_ylim(-1,28)
ax.set_xlabel('location')
ax.set_ylabel('abundance')
ax.legend()
plt.show()

こちらも緑本の図とほぼ同じ図になりました。