PyMC5でStick Breaking Processを実行してみる(ノンパラメトリックベイズ)

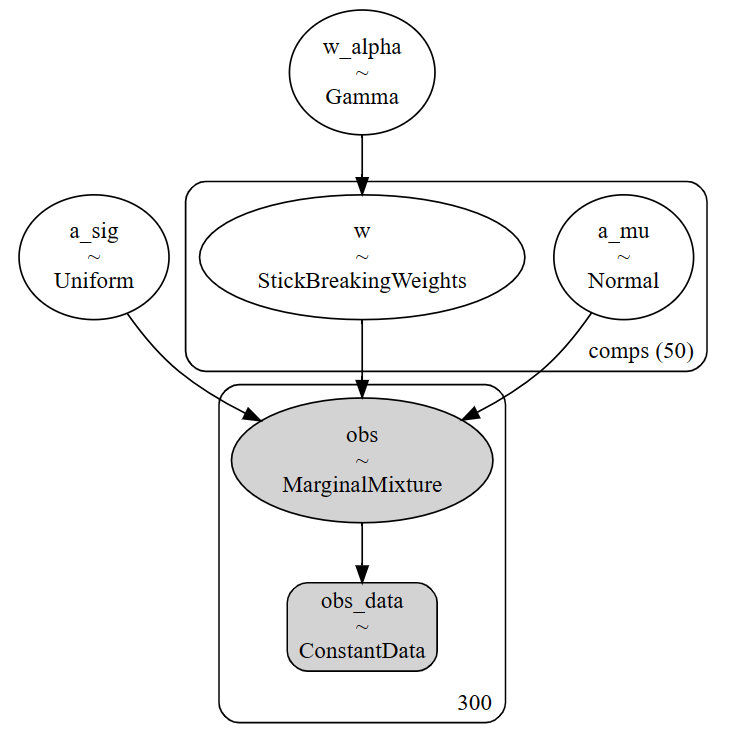
今回はPyMC5に実装されているStickBreakingWeights()でStick-Breaking Process(以下SBP)を使ってクラスター数を推定してみました。

SBPはノンパラメトリックベイズの一種で、SBP以外にもChinese Resturant Processなどがあります。この辺りの解説は以下の記事がわかりやすかったので、共有しておきます。

この記事では理論については触れずにひたすらSBPを実装していきます。実装は、PyMCの公式ドキュメントを参考にしました。

実装

実装はGoogle Colab(2024年3月16日現在)で行いました。

ライブラリ

使用したライブラリーは以下で読み込んでいるものです。Colabに入っているものをそのまま利用しました。

import pymc as pm
import numpy as np
import arviz as az
import matplotlib.pyplot as plt
import xarray as xr
import scipy as sp
import pandas as pd
import seaborn as sns

データセット

2峰性正規分布のようなデータを使用しました。SBPで2峰を推定できるか確かめてみます。

np.random.seed(0)
x1 = np.random.normal(10,10,100)
x2 = np.random.normal(50,10,200)
simulated_data = np.concatenate([x1,x2])
plt.hist(simulated_data)

モデリング

モデルは以下のように記述しました。

pm.StickBreakingWeights(alpha, K)が今回の主役です。混合正規分布で最終的に尤度計算をしますが、50個の正規分布から構成される混合正規分布の各分布の重みのパラメータになります。alphaが変化することで重みが0以上になるパラメータ数が変化するみたいです。

本来のSBPではコンポーネント数は無限ですが、MCMCでは計算の都合上有限個になります。

# SBPモデル
class model_sbp(pm.Model):
    def __init__(self, data, n_max_comp):
        super().__init__()
        self.add_coord('comps',np.arange(n_max_comp))
        obs_data = pm.ConstantData('obs_data', data)

        # 各コンポーネントの重みパラメータ
        w_alpha = pm.Gamma("w_alpha", 1.0, 1.0)
        w = pm.StickBreakingWeights(
                'w', alpha = w_alpha, K = n_max_comp-1,
                dims = 'comps')

        # N個の正規分布に順序を付けて識別可能にする
        a_mu = pm.Normal(
                    'a_mu', mu = 0, sigma = 10, dims = 'comps', 
                    transform = pm.distributions.transforms.ordered, 
                    initval = np.linspace(-10, 100, n_max_comp))
        a_sig = pm.Uniform('a_sig', lower = 0, upper = 100)
        comps = pm.Normal.dist(mu = a_mu, sigma = a_sig)

        # 混合正規分布
        obs = pm.Mixture('obs', w = w, comp_dists = comps, observed = obs_data)

# オブジェクト化        
mod = model_sbp(simulated_data, 50)
pm.model_to_graphviz(mod)

結果の確認

重みのパラメータwと混合正規分布のハイパーパラメータa_muを確認すると、1個の正規分布とそれ以外の正規分布の塊という感じの推定結果になっていそうです。

az.plot_trace(idata)
plt.tight_layout()

事後分布とデータの重ね合わせ

まず、事後確率密度を計算します。

# 結果図示用データの生成

# X軸用のデータを生成
x_plot = xr.DataArray(np.arange(np.min(simulated_data), np.max(simulated_data),step=0.1), dims=["plot"])
# 事後分布から確率密度を計算
post_pdf_contribs = xr.apply_ufunc(sp.stats.norm.pdf, x_plot, idata.posterior["a_mu"], idata.posterior["a_sig"])
# 重みの事後分布で確率密度を調整
post_pdfs = (idata.posterior["w"] * post_pdf_contribs).sum(dim=("comps"))
# 95%信用区間の上限と下限を計算
# post_pdf_quantiles = post_pdfs.quantile([0.025, 0.975], dim=("chain", "draw"))

# 模擬データをデータフレームに変換
data_df = pd.DataFrame({'simulated_data':simulated_data})

続いて模擬データと事後確率密度を重ね合わせてプロットします。

# 図示
fig, ax = plt.subplots(figsize=(8, 6))
# サンプルから100個抽出して確率密度をプロット
ax.plot(x_plot, az.extract(post_pdfs, var_names="x", num_samples=100), c="gray", alpha=0.4)
# 平均事後確率密度をプロット
ax.plot(x_plot, post_pdfs.mean(dim=("chain", "draw")), c="k", label="Posterior expected density")
# データをヒストグラムとしてプロット
sns.histplot(x='simulated_data',ax=ax,data=data_df,stat="density")
ax.legend()
plt.show()

モデルとしてはデータにいい感じで当てはまっているようです。ただし、上述の通りパラメータからコンポーネント数を判定できるかはかなり微妙な感じです。モデルの工夫が必要かもしれませんね。

プログラムはこちらに置いておきます。
https://colab.research.google.com/github/HKimura787/blog/blob/main/Qiita/SBP.ipynb