1. 概要
配送車両が複数の顧客に荷物を届ける際、最も効率的な道順を決定することは、極めて重要なポイントとなります。
この記事では、こうした課題の解消でキーとなってくる「ルート最適化」について、Python プログラミング言語を使いながら説明していこうと思います。
2. ルート最適化とは
ルート最適化とは、特定の目的地への移動やタスクの実行において、最も効率的かつ経済的なルートを決定するプロセスです。これは、特に物流、配送サービス、交通計画、営業訪問など、多くの場所に移動する必要がある分野で重要な要素と言えます。ルート最適化の主な目的は、時間、燃料、距離、コストを最小限に抑えることによって、全体の効率を最大化することです。
ルート最適化は、GPS ナビ、経路計画ツールなど、多くのソリューションで利用されています。これにより、企業は配送効率を高め、運用コストを削減し、顧客サービスを向上させることができます。
3. 歴史的背景
この問題の起源は1930年代にさかのぼります。当時、学校のバスのルートを数学的に最適化する試みが行われました。これは「巡回セールスマン問題 (Traveling Salesman Problem)」として知られており、ドライバーが各地点を効率的に巡る最適な順序を見つけることを目的としていました。
その後、これは配送コストと顧客の好みを考慮した車両のルート決定する「運搬経路問題 (Vehicle Routing Problem)」へと進化ていきました。例えば、夕食の配達を行う際に、夜間の交通量が多かったり、料金が高いルートは選ばないようにするといったことができるようになります。
4. Python による解決アプローチ
ここでは、Python を使用してルート最適化問題に取り組む方法を、実際のコード例とその解説を交えて紹介していきます。
データセットとしてスターバックスの店舗データを利用し、店舗の位置情報を基に最適なルートを計算するプロセスについて段階的に学んでいきます。
- 初期設定: 必要なツールを準備し、地理データを読み込み、地図上に表示します。
- ネットワークグラフの作成と最短経路の計算: 道路のネットワークを作り、最短経路を計算します。
- 前処理: 配送に必要な距離を計算します。
- 巡回セールスマン問題の解決: 単純なルート最適化問題を解決します。
- 運搬経路問題の解決: より複雑なルート最適化問題を解決します。
4.1. 初期設定
4.1.1. ライブラリのインポート
最初に使用するライブラリをインポートしておきます。
## データ用
import pandas as pd # データ分析と操作のための高性能なデータ構造(データフレームなど)を提供
import numpy as np # 数値計算を効率的に行うための多次元配列オブジェクトと関連するツールを提供
## プロット用
import matplotlib.pyplot as plt # データの可視化とグラフ作成のための機能を提供
import seaborn as sns # 統計的データ可視化をサポート
import folium # Leaflet.js を使用した地理空間データの可視化
from folium import plugins # folium ライブラリのための追加機能やプラグインを提供
import plotly.express as px # インタラクティブなグラフとデータ可視化を簡単に作成するためのハイレベルなインターフェースを提供
## 単純ルーティング用
import osmnx as ox # OpenStreetMap のデータを取得、構築、分析し、ネットワーク分析を行う
import networkx as nx # 複雑なネットワークの作成、操作、研究の用途
## 高度なルーティング用
from ortools.constraint_solver import pywrapcp # OR-Tools で、制約プログラミングをサポートする Python ラッパー。
from ortools.constraint_solver import routing_enums_pb2 # OR-Tools で、ルーティング問題に関連する列挙型と定数を提供するモジュール
4.1.2. データの準備
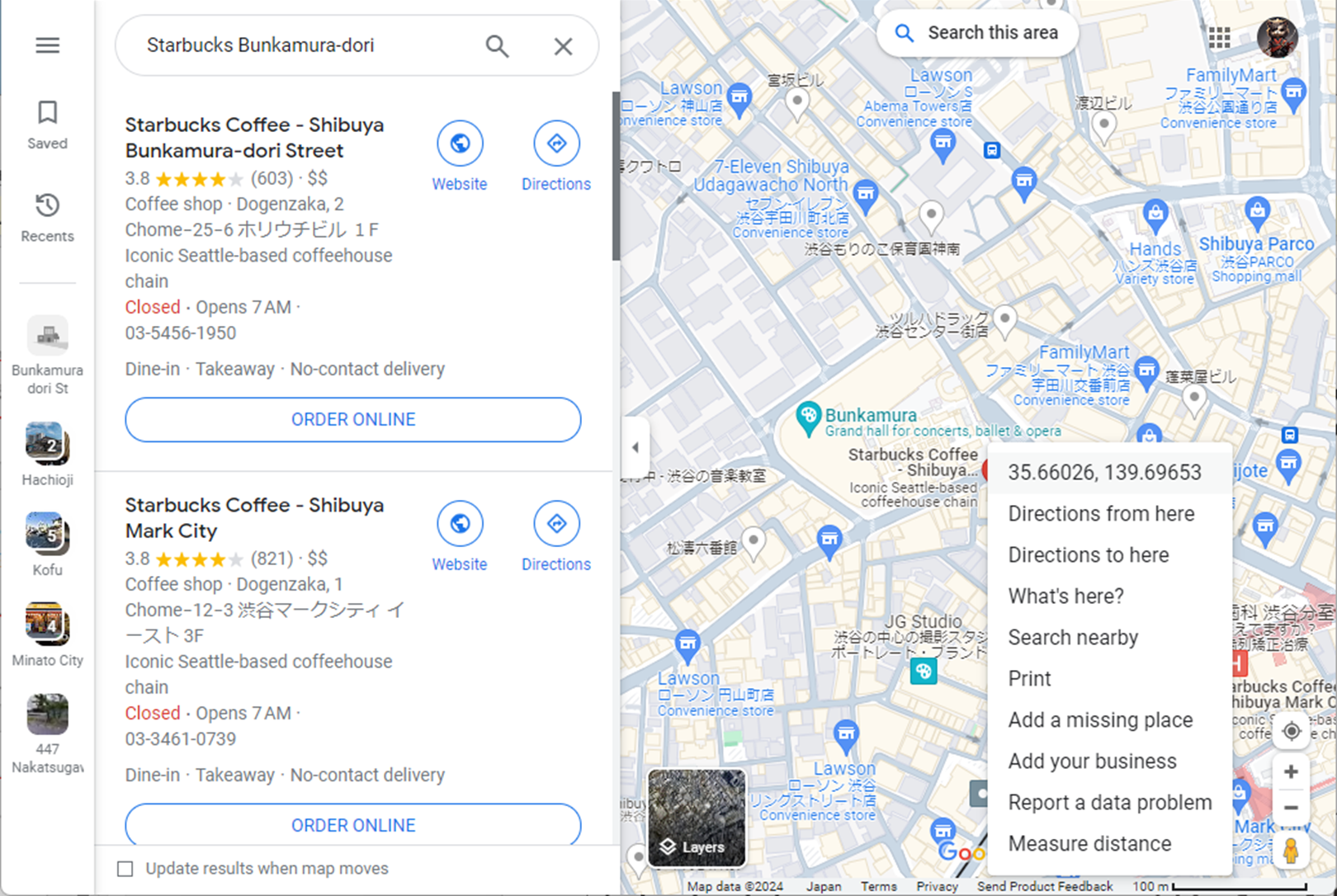
この記事では、データとして、kaggle の Starbucks Locations Worldwide から、directory.csv ファイルをダウンロードし、starbucks_stores.csv にリネームして使用します。
4.1.3. データの読み込み
CSV ファイルを読み込み、都市が「渋谷区」であるデータを抽出します。
# データセットとして使用する CSV ファイルを読み込み、データフレームに格納
dtf = pd.read_csv('starbucks_stores.csv')
# City 列が 'Shibuya-ku' である行を抽出し、
# City, Street Address, Latitude, Longitude 列のみを選択した後にインデックスを更新
city = "Shibuya-ku"
dtf = dtf[dtf["City"]==city][
["City","Street Address","Latitude","Longitude"]
].reset_index(drop=True)
インデックスを更新し、処理しやすいよう列名を変更します。
# index を 'id' に、Latitude 列を 'y' に、Longitude を 'x' にそれぞれ変更
dtf = dtf.reset_index().rename(
columns={"index":"id", "Latitude":"y", "Longitude":"x"})
渋谷区のデータが抽出されており、id、City、Street Address、y、x 列がセットされていることを確認します。
print("総数:", len(dtf))
dtf.head(3)
4.1.4. 基点とする場所の設定
データフレームの各行に対して、id 列が特定の値 (今回は 0) と一致するかどうかを判定し、一致する場合は 1 を、そうでない場合は 0 を base 列に格納します。
次に、base 列が 1 である行を見つけ、その行の y と x の値を取得します。
以降の手順では、ここで設定した基点からその他のすべての場所に移動するための最適な方法を計算していきます。
# id が 0 の場所を基点として設定
i = 0
# id が i (ここでは 0) と等しい場合に 1 を、そうでない場合に 0 を 'base' 列に代入
dtf["base"] = dtf["id"].apply(lambda x: 1 if x==i else 0)
# base 列が 1 である行をフィルタリングし、その行の y 列と x 列の値を取得
start = dtf[dtf["base"]==1][["y","x"]].values[0]
start 変数には x 座標および y 座標がリスト形式で格納されており、データフレームには新たに base 列がセットされていることを確認することができます。
print("start =", start)
dtf.head(3)
4.1.5. 各場所の座標を可視化
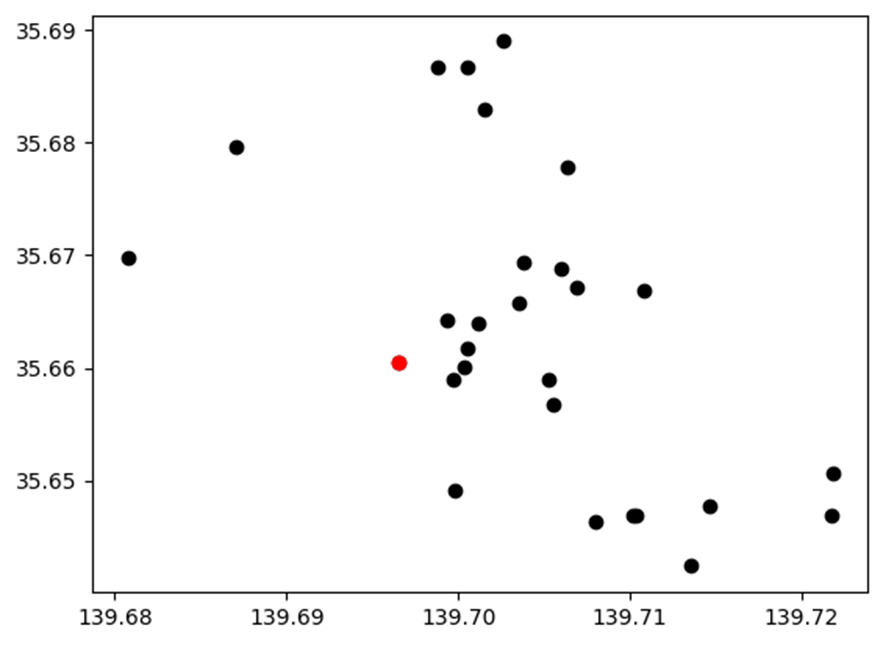
基点となる場所の座標(赤色)とその他の座標(黒色)をプロットして確認してみます。
plt.scatter(y=dtf["y"], x=dtf["x"], color="black")
plt.scatter(y=start[0], x=start[1], color="red")
plt.show()
4.1.6. 地図上へのデータポイントの表示
データの視覚化を行うことにより、情報の理解を容易にすることができるようになります。地理的なデータを扱う際には、地図上で正確に表示することが重要となってきます。この記事では、データポイントを地図上に効果的に表示するために、Folium というライブラリを使用します。
Folium は、HTML を駆使して様々なタイプのインタラクティブなマップを作成できるライブラリです。このツールを使用することで、地図上にデータポイントを表示することが可能になります。
'''
folium でマップを作成する。
:パラメータ
param dtf: pandas
param (y,x): str - (緯度,経度) を要素とする列
param starting_point: list - (緯度,経度) を指定
param tiles: str - "cartodbpositron", "OpenStreetMap", "Stamen Terrain", "Stamen Toner".
param popup: str - クリックされたときにポップアップするテキストを指定する列
:param size: str - サイズを変数で指定する列,None の場合は size=5 となる
:param color: str - 変数 color を指定する列,None の場合はデフォルトの色になる
:param lst_colors: list - 色の列が None でない場合に利用される、複数の色のリスト
param marker: str - 変数 marker を指定する列,最大 7 個のユニークな値を取る
:戻り値
表示するマップオブジェクト
'''
def plot_map(dtf, y, x, start, zoom=12, tiles="cartodbpositron", popup=None, size=None, color=None, legend=False, lst_colors=None, marker=None):
data = dtf.copy()
## プロットのためのカラムを作成
if color is not None:
lst_elements = sorted(list(dtf[color].unique()))
lst_colors = ['#%06X' % np.random.randint(0, 0xFFFFFF) for i in range(len(lst_elements))] if lst_colors is None else lst_colors
data["color"] = data[color].apply(lambda x: lst_colors[lst_elements.index(x)])
if size is not None:
scaler = preprocessing.MinMaxScaler(feature_range=(3,15))
data["size"] = scaler.fit_transform(data[size].values.reshape(-1,1)).reshape(-1)
## マップ
map_ = folium.Map(location=start, tiles=tiles, zoom_start=zoom)
if (size is not None) and (color is None):
data.apply(lambda row: folium.CircleMarker(location=[row[y],row[x]], popup=row[popup],
color='#3186cc', fill=True, radius=row["size"]).add_to(map_), axis=1)
elif (size is None) and (color is not None):
data.apply(lambda row: folium.CircleMarker(location=[row[y],row[x]], popup=row[popup],
color=row["color"], fill=True, radius=5).add_to(map_), axis=1)
elif (size is not None) and (color is not None):
data.apply(lambda row: folium.CircleMarker(location=[row[y],row[x]], popup=row[popup],
color=row["color"], fill=True, radius=row["size"]).add_to(map_), axis=1)
else:
data.apply(lambda row: folium.CircleMarker(location=[row[y],row[x]], popup=row[popup],
color='#3186cc', fill=True, radius=5).add_to(map_), axis=1)
## tiles
# タイルセットを追加
layers = {
"cartodbpositron": None, # 組み込みレイヤー
"openstreetmap": None, # 組み込みレイヤー
"Stamen Terrain": "http://tile.stamen.com/terrain/{z}/{x}/{y}.jpg",
"Stamen Water Color": "http://tile.stamen.com/watercolor/{z}/{x}/{y}.jpg",
"Stamen Toner": "http://tile.stamen.com/toner/{z}/{x}/{y}.png",
"cartodbdark_matter": None # 組み込みレイヤー
}
# タイルレイヤーをマップに追加するループ
for name, url in layers.items():
if url:
# カスタムタイルレイヤーを追加
folium.TileLayer(
tiles=url,
attr='Map data © OpenStreetMap contributors, Stamen Design',
name=name
).add_to(map_)
else:
# 組み込みタイルレイヤーを追加
folium.TileLayer(name).add_to(map_)
## 凡例
if (color is not None) and (legend is True):
legend_html = """<div style="position:fixed; bottom:10px; left:10px; border:2px solid black; z-index:9999; font-size:14px;"> <b>"""+color+""":</b><br>"""
for i in lst_elements:
legend_html = legend_html+""" <i class="fa fa-circle fa-1x" style="color:"""+lst_colors[lst_elements.index(i)]+""""></i> """+str(i)+"""<br>"""
legend_html = legend_html+"""</div>"""
map_.get_root().html.add_child(folium.Element(legend_html))
## マーカーの追加
if marker is not None:
lst_elements = sorted(list(dtf[marker].unique()))
lst_colors = ["yellow","red","blue","green","pink","orange","gray"] #7
### 値が多すぎてマークできない場合
if len(lst_elements) > len(lst_colors):
raise Exception("マーカーの一意な値が " + str(len(lst_colors)) + " 個を超えています")
### 二値のケース(1/0): 1だけをマーク
elif len(lst_elements) == 2:
data[data[marker]==lst_elements[1]].apply(lambda row: folium.Marker(location=[row[y],row[x]], popup=row[marker], draggable=False,
icon=folium.Icon(color=lst_colors[0])).add_to(map_), axis=1)
### 通常のケース:全ての値をマーク
else:
for i in lst_elements:
data[data[marker]==i].apply(lambda row: folium.Marker(location=[row[y],row[x]], popup=row[marker], draggable=False,
icon=folium.Icon(color=lst_colors[lst_elements.index(i)])).add_to(map_), axis=1)
## フルスクリーン
plugins.Fullscreen(position="topright", title="展開", title_cancel="退出", force_separate_button=True).add_to(map_)
return map_
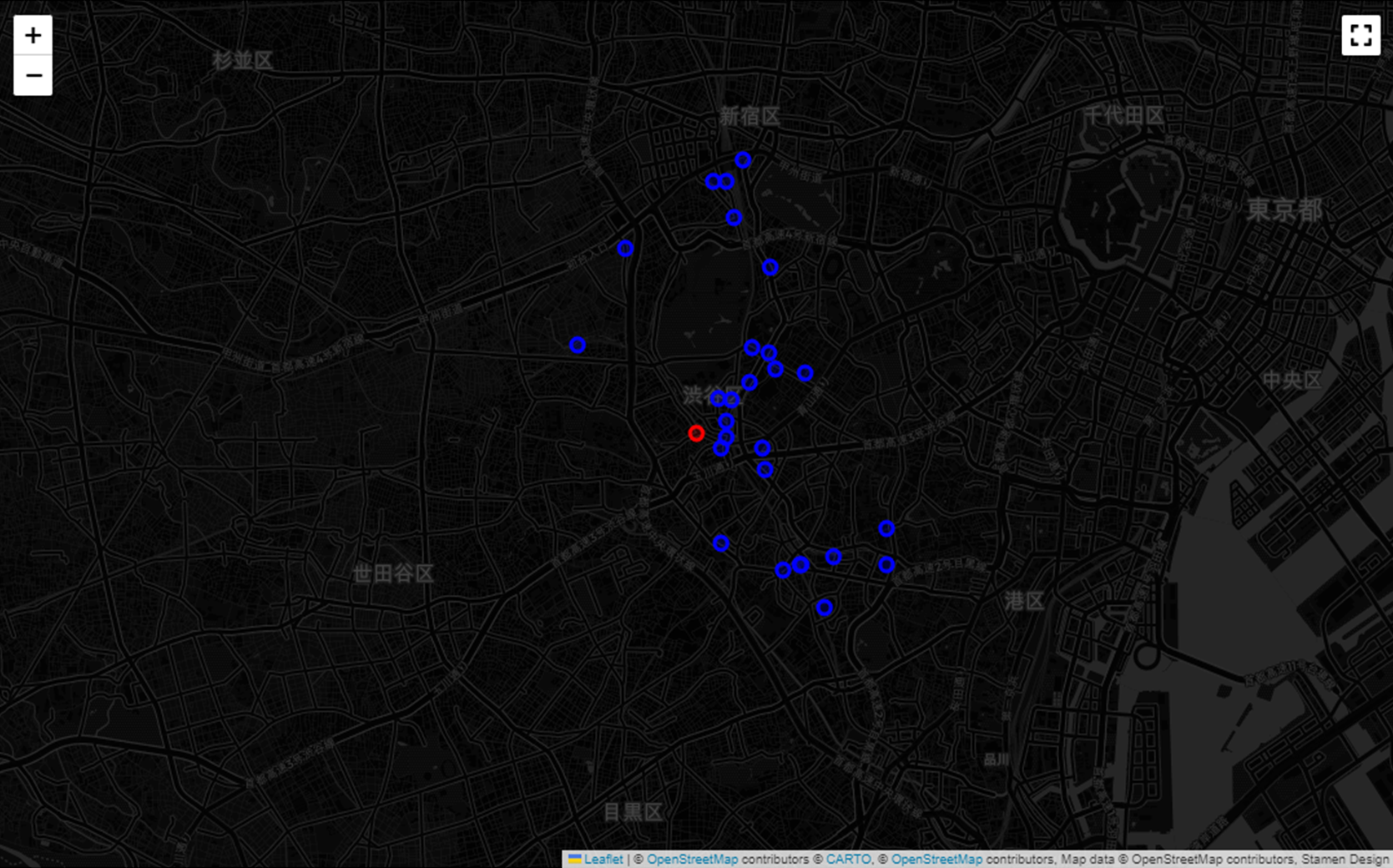
map_ = plot_map(dtf, y="y", x="x", start=start, zoom=13,
tiles="cartodbpositron", popup="id",
color="base", lst_colors=["blue", "red"])
map_
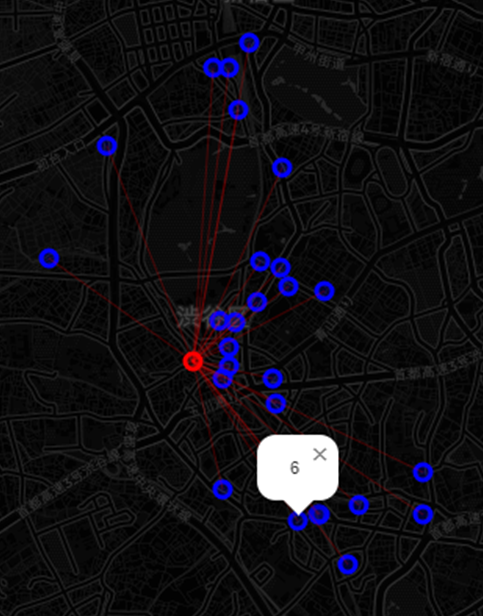
4.1.7. 基点となる場所と他の場所とをつなぐ線の描画
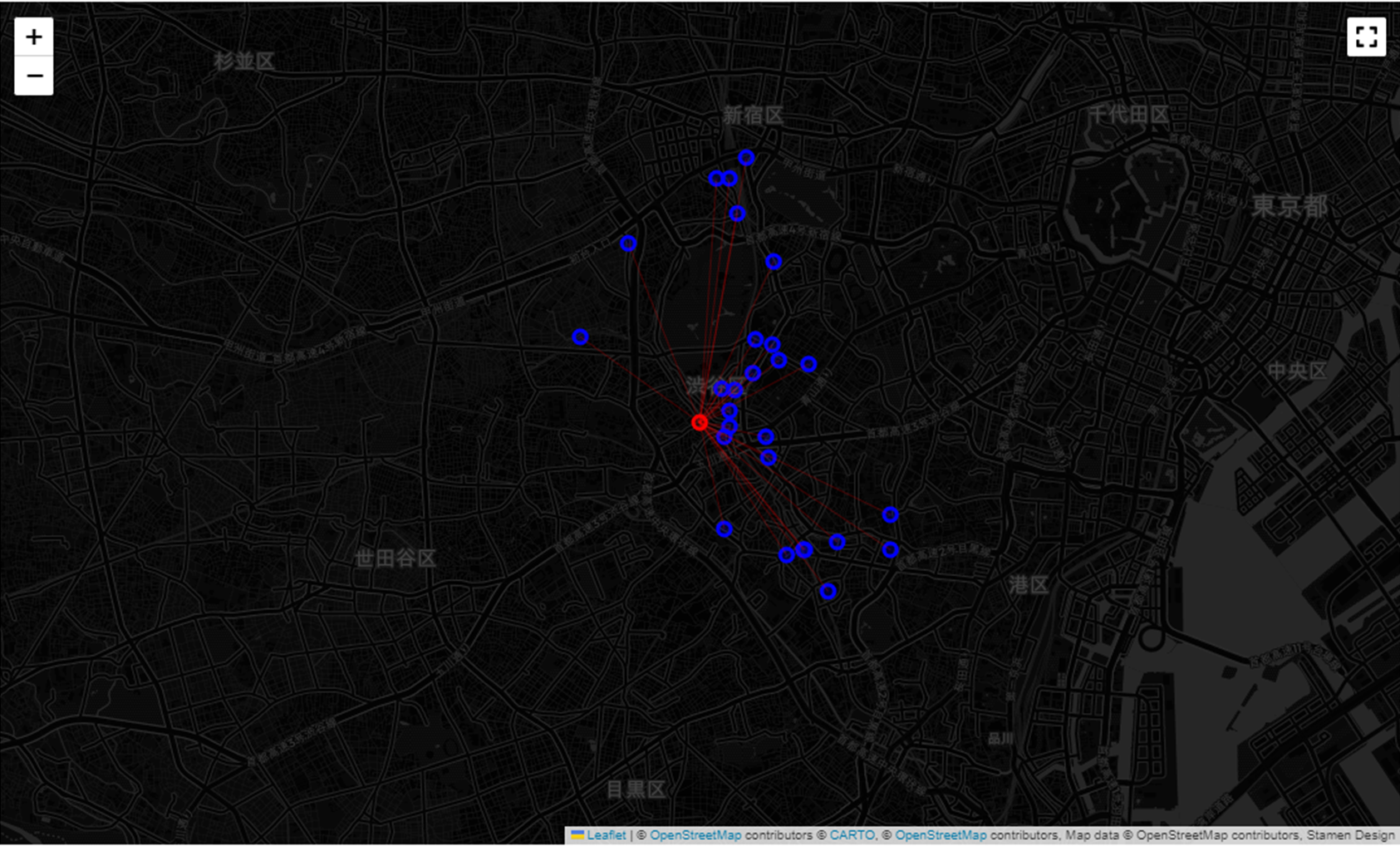
続けて、基点となる場所から他のすべての場所への経路を地図上に可視化してみます。
# 線を追加する処理
for i in range(len(dtf)):
# 'start' 位置とデータフレームの各行の 'y' と 'x' の値を使用して点のリストを作成
points = [start, dtf[["y","x"]].iloc[i].tolist()]
# 作成した点のリストを使用して、地図上に PolyLine(線)を描画
# - 線の色: 赤
# - 重さ: 0.5
# - 透明度: 0.5
folium.PolyLine(points, color="red", weight=0.5, opacity=0.5).add_to(map_)
# 地図を表示
map_
4.2. ネットワークグラフの作成と最短経路の計算
4.2.1. 道路ネットワークの視覚化
実際に移動する際は直線で移動することはできず、道路に沿って移動することになります。そこで、道路ネットワークを用いた分析を行います。
ここでは道路ネットワークをグラフとして扱い、ノード間の最短経路を見つけるようにします。
# ネットワークグラフの作成
# - 'start'の位置から半径10000メートル以内の道路ネットワークを取得
# - 道路の種類として自動車用の道路 ("drive") を指定
G = ox.graph_from_point(start, dist=10000, network_type="drive") #'drive', 'bike', 'walk'
# グラフの各エッジ(道路)に速度を追加
G = ox.add_edge_speeds(G)
# グラフの各エッジに旅行時間を追加
G = ox.add_edge_travel_times(G)
# グラフのプロット
# - 背景色: 黒
# - ノードのサイズ: 5
# - ノード色: 白
# - 図のサイズ: 幅16インチ、高さ8インチ
fig, ax = ox.plot_graph(G, bgcolor="black", node_size=5, node_color="white", figsize=(16,8))
G.nodes.data() でノード情報を確認することができます。データには、x 軸、y 軸、接続されている道路数 ('street_count') とその他の付加情報が含まれています。
NodeDataView({
31236584: {'y': 35.6349354, 'x': 139.7686834, 'ref': '1101', 'highway': 'motorway_junction', 'street_count': 3},
31236646: {'y': 35.6344166, 'x': 139.7779888, 'street_count': 3},
31236657: {'y': 35.6334763, 'x': 139.778439, 'street_count': 3},
31236735: {'y': 35.6429833, 'x': 139.7577172, 'street_count': 3},
31236737: {'y': 35.6405492, 'x': 139.756849, 'highway': 'traffic_signals', 'street_count': 4},
...
11500443395: {'y': 35.6381751, 'x': 139.6413934, 'street_count': 3}
})
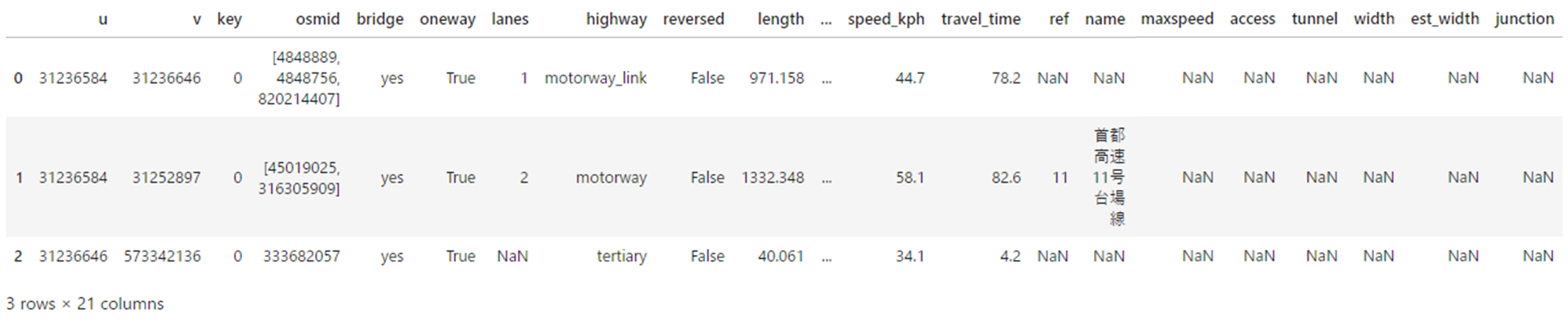
同様に G.edges.data() でエッジ情報を確認することができます。'speed_kph' および 'travel_time' もセットされていることを確認することができます。
OutMultiEdgeDataView([
(31236584, 31236646, {
'osmid': [4848889, 4848756, 820214407],
'bridge': 'yes',
'oneway': True,
'lanes': '1',
'highway': 'motorway_link',
'reversed': False,
'length': 971.1579999999999,
'geometry': <LINESTRING (139.769 35.635, 139.769 35.635, 139.769 35.635, 139.769 35.635,...>,
'speed_kph': 44.8,
'travel_time': 78.0
}),
(31236584, 31252897, {
'osmid': [45019025, 316305909],
'bridge': 'yes',
'oneway': True,
'lanes': '2',
'ref': '11',
'name': '首都高速11号台場線',
'highway': 'motorway',
'reversed': False,
'length': 1332.3480000000004,
'geometry': <LINESTRING (139.769 35.635, 139.769 35.635, 139.769 35.635, 139.769 35.635,...>,
'speed_kph': 58.0,
'travel_time': 82.7
}),
(31236646, 573342136, {
'osmid': 333682057,
'bridge': 'yes',
'oneway': True,
'highway': 'tertiary',
'reversed': False,
'length': 40.061,
'speed_kph': 34.1,
'travel_time': 4.2
}),
(31236657, 298984113, {
'osmid': 863283179,
'bridge': 'yes',
'oneway': True,
'highway': 'tertiary',
'reversed': False,
'length': 101.079,
'speed_kph': 34.1,
'travel_time': 10.7}),
(31236657, 2805815248, {
'osmid': [4848755, 820103843, 4847509],
'bridge': 'yes',
'oneway': True,
'highway': 'motorway_link',
'reversed': False,
'length': 1035.475,
'lanes': '1',
'geometry': <LINESTRING (139.778 35.633, 139.778 35.634, 139.778 35.634, 139.777 35.635,...>,
'speed_kph': 44.8,
'travel_time': 83.2
}),
...
(11500443395, 864255596, {
'osmid': 43063457,
'oneway': True,
'name': '大山街道旧道',
'highway': 'unclassified',
'reversed': False,
'length': 29.249,
'speed_kph': 27.9,
'travel_time': 3.8
}),
(11500443395, 1668738048, {
'osmid': 1238086660,
'highway': 'residential',
'oneway': False,
'reversed': True,
'length': 13.731,
'speed_kph': 27.2,
'travel_time': 1.8
})
])
4.2.2. MultiDiGraph から GeoDataFrame ノードへの変換
道路ネットワークグラフ (MultiDiGraph) から GeoDataFrame へ変換することにより、道路や交差点などのネットワーク要素に地理的情報を付加し、これらを地図上で効果的に表示および分析するといったことができるようになります。また、地理空間データの操作と可視化が容易になり、GIS ソフトウェアとの互換性が向上します。
ひとまず GeoDataFrame ノードへの変換を行います。
# グラフ G のノード数を出力
print("ノード数:", len(G.nodes()))
# グラフ G から GeoDataFrame を作成
# - nodes=True: ノードのデータを取得する
# - edges=False: エッジのデータは取得しない
ox.graph_to_gdfs(G, nodes=True, edges=False).reset_index().head(3)
4.2.3. MultiDiGraph から GeoDataFrames リンクへの変換
同様に GeoDataFrame リンクへの変換を行います。
# グラフ G のエッジ(リンク)数を出力
print("リンク数:", len(G.edges()))
# グラフ G から GeoDataFrame を作成
# - nodes=False: ノードのデータは取得しない
# - edges=True: エッジ(リンク)のデータを取得する
ox.graph_to_gdfs(G, nodes=False, edges=True).reset_index().head(3)
4.2.4. 任意の目的地の設定
グラフが完成したので、ここからは2ノード間を移動する方法について考えていきます。
開始位置はすでに設定済みなので、任意の終了位置のみ設定します。
# id 列が '6' である行を抽出し、その行の y と x の値を取得し、終了位置としてセット
end = dtf[dtf["id"]==6][["y","x"]].values[0]
# 開始位置(start)と終了位置(end)を出力
print("地点: from", start, "--> to", end)
地点: from [ 35.66047469 139.6965412 ] --> to [ 35.64627453 139.7079937 ]
4.2.5. 開始位置と終了位置に近い GeoDataFrames ノードの検出
OSMnx を使用し、開始位置と終了位置に近い GeoDataFrames ノードを検出します。
# グラフ G 内で、指定された開始位置(start)に最も近いノードを探す
# - start[1]: 経度
# - start[0]: 緯度
start_node = ox.distance.nearest_nodes(G, start[1], start[0])
# 終了位置(end)に最も近いノードを探す
# - start[1]: 経度
# - start[0]: 緯度
end_node = ox.distance.nearest_nodes(G, end[1], end[0])
# 開始ノードと終了ノードの ID を出力
print("ノード: from", start_node, "--> to", end_node)
ノード: from 1014529751 --> to 741609952
4.2.6. 最短経路問題を解くためのアルゴリズム
最短経路問題を解くためのアルゴリズムには様々なものがあり、グラフの特性(エッジの重みが負かどうか等)や問題の要件(特定のノード間の最短経路を見つけるか、全ノード間の最短経路を見つけるか等)に応じて適したものを選択します。代表的なものについて、それぞれの特徴と利点、制約について以下に示します。
-
ダイクストラ法 (Dijkstra's Algorithm)
- 特徴: 単一の出発点から他のすべてのノードへの最短経路を見つけます。非負のエッジ重みに対応。
- 利点: 効率的で、実装が比較的簡単。
- 制約: 負の重みを持つエッジには対応していません。
-
ベルマン-フォード法 (Bellman-Ford Algorithm)
- 特徴: 単一の出発点から他のすべてのノードへの最短経路を見つけます。負の重みを持つエッジに対応。
- 利点: 負の重みサイクルの存在を検出できます。
- 制約: ダイクストラ法より計算効率が低い。
-
フロイド-ワーシャル法 (Floyd-Warshall Algorithm)
- 特徴: すべてのノードペア間の最短経路を見つけます。負の重みを持つエッジに対応。
- 利点: 全ノード間の最短経路を一度に計算できます。
- 制約: 大規模なグラフではメモリ使用量が大きくなります。
-
Aアルゴリズム (A Algorithm)
- 特徴: ヒューリスティックを用いて特定の目的地への最短経路を効率的に見つけます。
- 利点: 効率的で、特に地図上の経路探索に適しています。
- 制約: ヒューリスティックの選択が結果に影響します。
-
ジョンソンのアルゴリズム (Johnson's Algorithm)
- 特徴: すべてのノードペア間の最短経路を見つけます。負の重みを持つエッジに対応。
- 利点: ベルマン-フォード法とダイクストラ法を組み合わせて、効率的に最短経路を計算します。
- 制約: 実装が複雑で、大規模なグラフでは計算時間が長くなる可能性があります。
4.2.7. 距離ベースによる最短経路の計算
今回は、ネットワーク内の2つのノード間の最短経路を簡単に見つけることのできるダイクストラ法を使用して、最短経路の計算を行っていきます。
ダイクストラ法は、実装が容易で、特に小~中規模のグラフでは高い効率性を発揮する一方で、以下のような制限もあるので注意してください。
- 出発点となるノードから始まり、隣接するノードへと最短経路を段階的に拡張していくことで、目的のノードまでの全体のルートを計算するため、全ノード間の最短経路の計算は行えない。
- 負の重みを持つエッジがある場合、このアルゴリズムは正しい結果を保証されない。
- 大規模なグラフでは、計算コストが高くなり、比較的多くのメモリを消費する可能性がある。
- グラフの構造が頻繁に変化する場合、アルゴリズムの再実行が必要となる。
Python 実装では NetworkX ライブラリを利用することで、簡単にダイクストラ法を実装することができます。このライブラリを使用すると、ノード間の経路を最適化する際に、重みを距離や移動時間などに容易に変更し、重みが最小となるパスを最短経路として得ることができます。
まずは、重みを距離に変更し、最短経路を計算します。
# 最短経路の計算
# グラフ G 上で start_node から end_node までの最短経路を計算
# ダイクストラ法を使用し、重みは 'lenght'(長さ)で計算
path_lenght = nx.shortest_path(G, source=start_node, target=end_node,
method='dijkstra', weight='lenght')
# 計算された経路を出力
print(len(path_lenght), "ノード -->", path_lenght)
33 ノード --> [1014529751, 252675826, 1108870926, 598416635, 252675828, 291758776, 9518528864, 1499530611, 2990668088, 1014530112, 10219242888, 309701965, 878251818, 2253585427, 617028987, 613396344, 613396359, 1074623823, 613396383, 613396315, 613396266, 613396248, 613396389, 1558976084, 614219168, 614219165, 613396227, 625489333, 340381520, 1708884904, 340381522, 2847803005, 741609952]
得られた経路をグラフ上に描画します。
# 計算された経路を地図上に描画
# - 経路の色: 赤
# - 線の太さ: 5
# - ノードのサイズ: 1
# - 背景色: 黒
# - ノードの色: 白
# - 図のサイズ: 幅16インチ、高さ8インチ
fig, ax = ox.plot_graph_route(G, path_lenght, route_color="red", route_linewidth=5,
node_size=1, bgcolor='black', node_color="white",
figsize=(16,8))
4.2.8. 移動時間ベースによる最短経路の計算
距離ベースの最適化と同じように、移動時間を最適化することで、より効率的な経路計画が可能になります。
指定された2つのノード間で最短の移動時間となる経路を計算します。
# グラフ G 上で start_node から end_node までの最短時間経路を計算
# ダイクストラ法を使用し、重みは 'travel_time'(移動時間)で計算
path_time = nx.shortest_path(G, source=start_node, target=end_node,
method='dijkstra', weight='travel_time')
# 計算された経路を出力
print(len(path_time), "ノード -->", path_time)
37 ノード --> [1014529751, 252675826, 1108870926, 598416635, 252675828, 291758776, 1316007410, 252683801, 1685220989, 1685220985, 1685220982, 1685220981, 5787345704, 1685220953, 1685220952, 1685220950, 1685220946, 9961640269, 1685220942, 1562273629, 1562273613, 1562273501, 1562273206, 2099195693, 1562273123, 1562273117, 196978962, 8944000163, 1705580436, 382020712, 251860136, 383209670, 340381520, 1708884904, 340381522, 2847803005, 741609952]
得られた経路をグラフ上に描画します。
# 計算された経路を地図上に描画
# - 経路の色: 青
# - 線の太さ: 5
# - ノードのサイズ: 1
# - 背景色: 黒
# - ノードの色: 白
# - 図のサイズ: 幅16インチ、高さ8インチ
fig, ax = ox.plot_graph_route(G, path_time, route_color="blue", route_linewidth=5,
node_size=1, bgcolor='black', node_color="white",
figsize=(16,8))
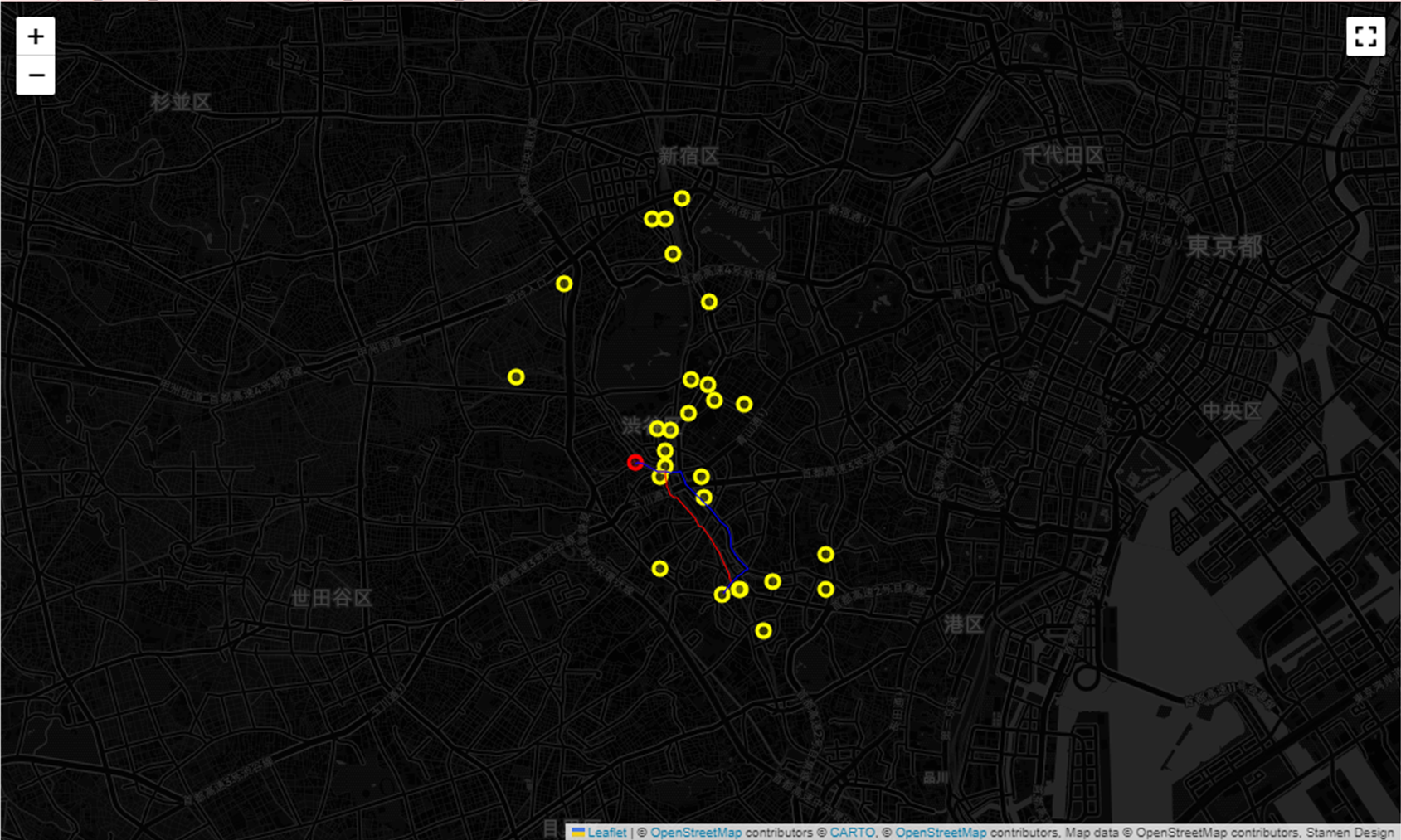
4.2.9. 距離ベースと移動時間ベースでの経路比較
OSMnx ライブラリを活用することで、道路ネットワークグラフ上に複数の経路を視覚的に描画し、比較することができます。
距離ベースと移動時間ベースでの経路計画がどのように違っているのか見比べてみましょう。
print('赤色ルート:',
round(sum(ox.utils_graph.get_route_edge_attributes(G,path_lenght,'length'))/1000, 2),
'km,',
round(sum(ox.utils_graph.get_route_edge_attributes(G,path_lenght,'travel_time'))/60, 2),
'分')
print('青色ルート:',
round(sum(ox.utils_graph.get_route_edge_attributes(G,path_time,'length'))/1000, 2),
'km,',
round(sum(ox.utils_graph.get_route_edge_attributes(G,path_time,'travel_time'))/60, 2),
'分')
赤色ルート: 2.24 km, 4.18 分
青色ルート: 2.45 km, 3.33 分
# グラフ G 上に複数の経路を描画
# - routes: 表示する経路のリスト(ここでは path_length と path_time)を指定
# - route_colors: 各経路の色を指定(ここでは赤と青)
# - route_linewidth: 経路の線の太さ
# - node_size: ノードのサイズ
# - bgcolor: 背景色
# - node_color: ノードの色
# - figsize: 図のサイズ(幅16インチ、高さ8インチ)
fig, ax = ox.plot_graph_routes(G, routes=[path_lenght, path_time],
route_colors=["red","blue"], route_linewidth=5,
node_size=1, bgcolor='black', node_color="white",
figsize=(16,8))
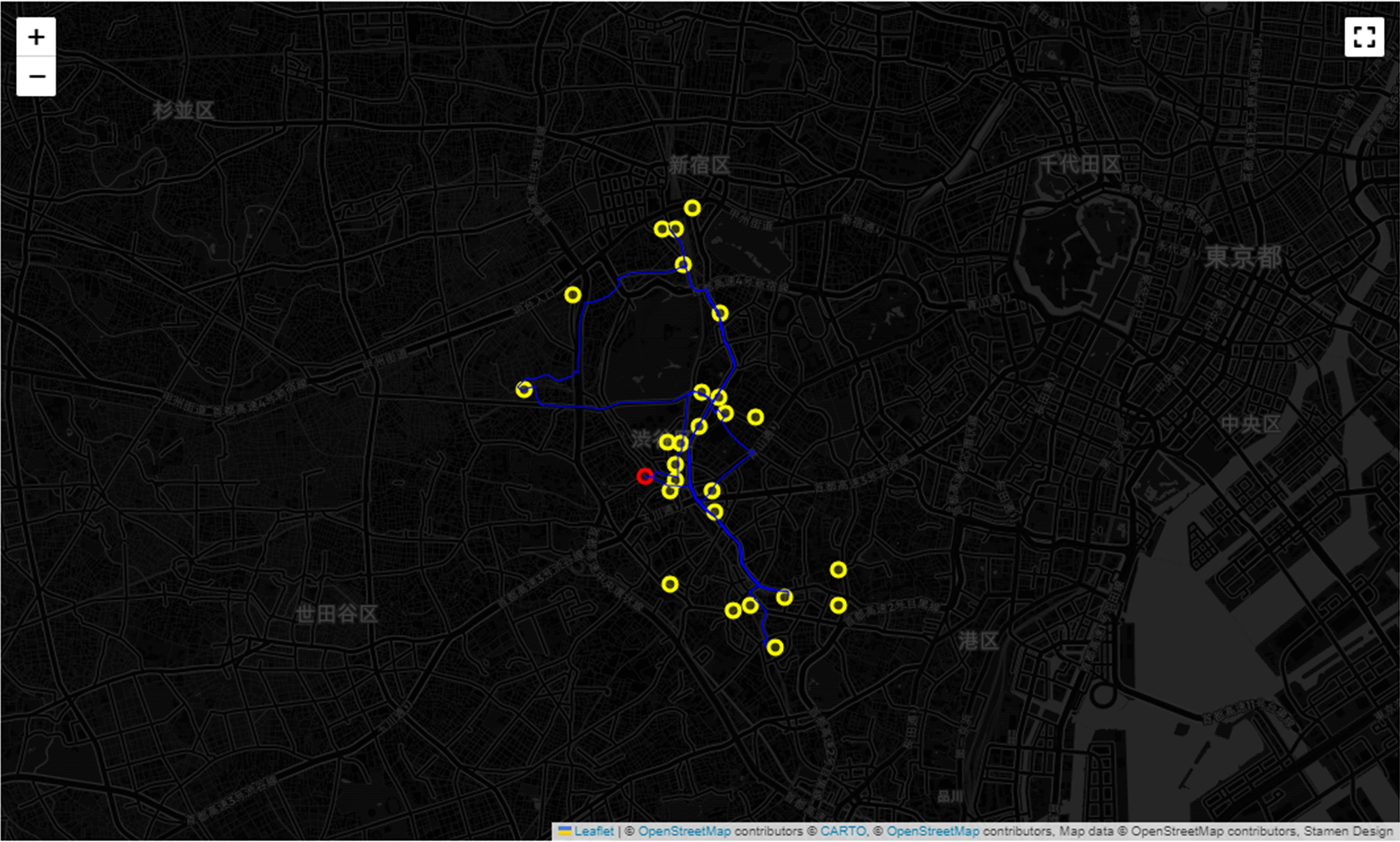
4.2.10. OSMnx ライブラリを使用した Folium 地図上への経路表示
OSMnx ライブラリの機能を活用し、Folium 地図上に経路をプロットすることで、経路の詳細をより明確に、視覚的に捉えることが可能になります。
# 前の手順で定義した plot_map 関数を使い、folium でマップを作成
map_ = plot_map(dtf, y="y", x="x", start=start, zoom=12,
tiles="cartodbpositron", popup="id",
color="base", lst_colors=["yellow","red"])
# グラフ G 上の経路 path_length を Folium 地図に描画
# - route_map: 既存のFolium地図オブジェクト(map_)を指定
# - 色: 赤
# - 線の太さ: 1
ox.plot_route_folium(G, route=path_lenght, route_map=map_, color="red", weight=1)
# 同様に、経路 path_time も Folium 地図上に描画
# - 色: 青
# - 線の太さ: 1
ox.plot_route_folium(G, route=path_time, route_map=map_, color="blue", weight=1)
# Folium 地図を表示
map_
4.2.11. ノード間の単一経路での移動シミュレーション
次の、ノードからノードへの移動をシミュレーションする方法について説明していきます。このシミュレーションでは、インタラクティブなプロット作成に適した Plotly ライブラリと、Lonely Planet や Financial Times などの有名な Web サイトで使用されているカスタムオンラインマップのプロバイダーである Mapbox を組み合わせて使用します。
まず、ルート情報が含まれたデータフレームを準備します。このデータフレームは、道路ネットワークグラフから特定の経路に関する詳細なデータを抽出し、整理したものです。
def df_animation_single_path(G, path):
# 経路に関するリストを初期化
lst_start, lst_end = [],[]
start_x, start_y = [],[]
end_x, end_y = [],[]
lst_length, lst_time = [],[]
# path_time 経路の各セグメントに対してループ処理
for a,b in zip(path[:-1], path[1:]):
# 経路の開始ノードと終了ノードをリストに追加
lst_start.append(a)
lst_end.append(b)
# 各セグメントの長さと移動時間をリストに追加
lst_length.append(round(G.edges[(a,b,0)]['length']))
lst_time.append(round(G.edges[(a,b,0)]['travel_time']))
# 開始ノードと終了ノードの x 座標(経度)と y 座標(緯度)をリストに追加
start_x.append(G.nodes[a]['x'])
start_y.append(G.nodes[a]['y'])
end_x.append(G.nodes[b]['x'])
end_y.append(G.nodes[b]['y'])
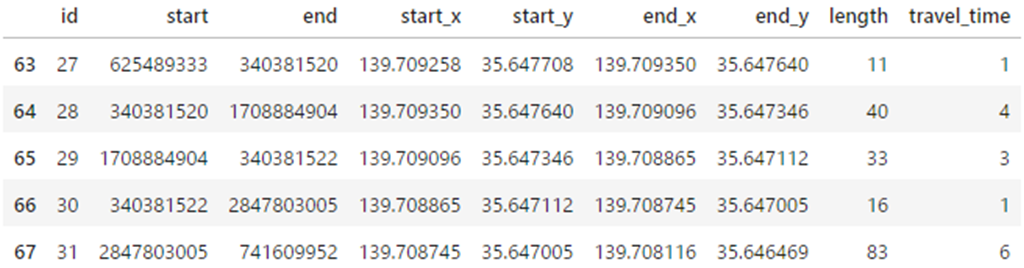
# 抽出したデータを Pandas DataFrame に変換
# 各列には、開始ノード、終了ノード、開始ノードの x 座標と y 座標、終了ノードの x 座標と y 座標、
# セグメントの長さ、移動時間が含まれる
df = pd.DataFrame(list(zip(lst_start, lst_end,
start_x, start_y,
end_x, end_y,
lst_length, lst_time)),
columns=["start", "end",
"start_x", "start_y",
"end_x", "end_y",
"length", "travel_time"]
).reset_index().rename(columns={"index":"id"})
return df
print("ノード: from", start_node, "--> to", end_node)
ノード: from 1014529751 --> to 741609952
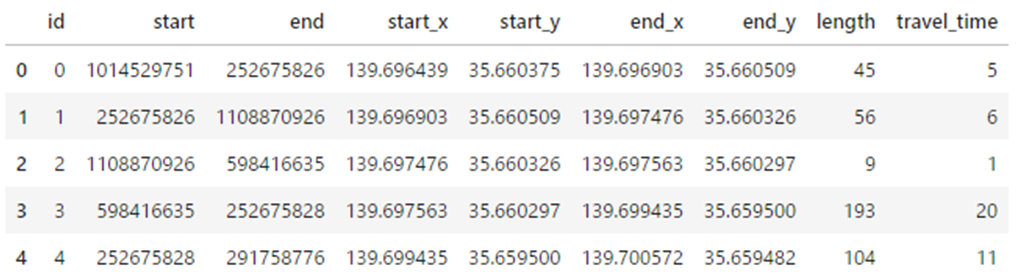
df = df_animation_single_path(G, path_time)
df.head()
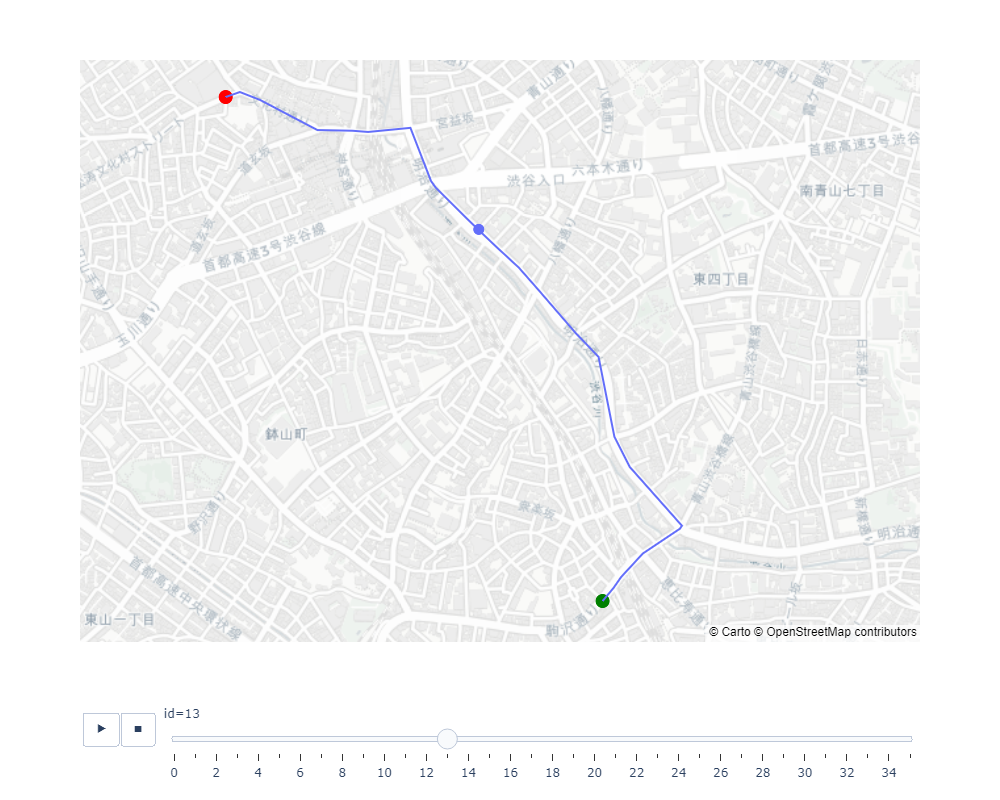
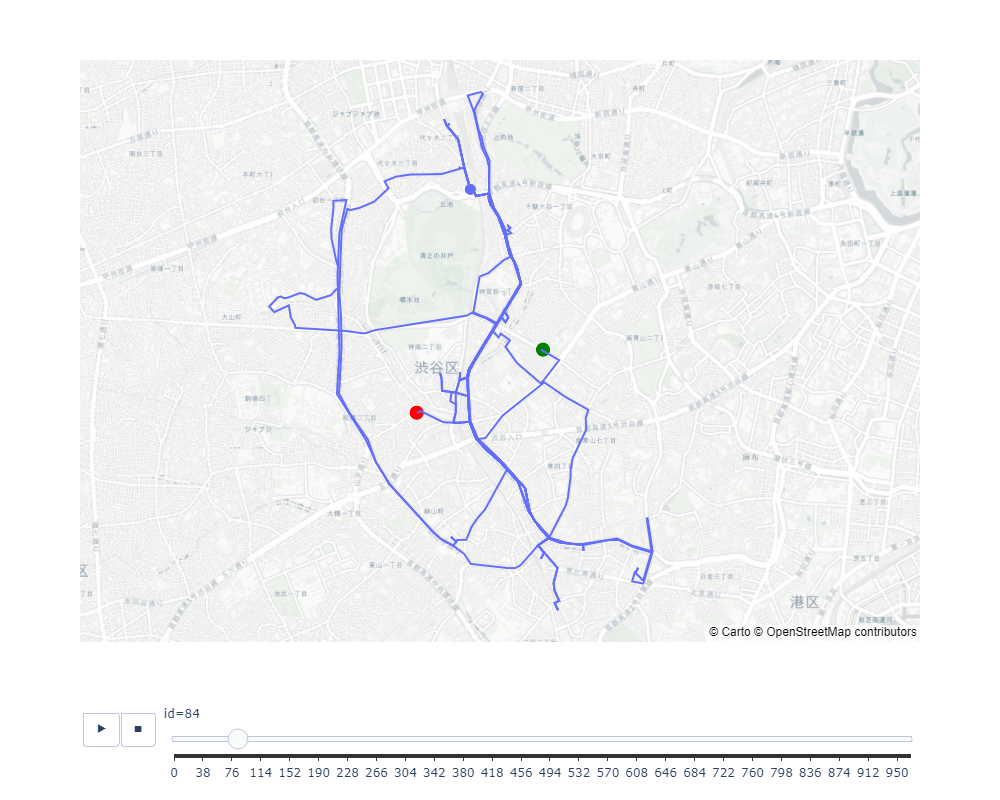
次に、このデータを基に Plotly アニメーションを作成し、ドライバーがノード間を移動する様子を視覚的に表現します。
Plotly Express に Mapbox を組み合わせることで、地図上に経路と重要なポイントを効果的に可視化することができます。この方法では、経路全体とその上の特定のポイント(例えば、開始点と終了点)を表示するようにします。
開始点と終了点はそれぞれ赤と緑のマーカーで表示され、経路上の移動点(ドライバーの位置など)はアニメーションとして表現されます。
この視覚化により、経路の全体的な形状と、特定のポイント間の位置関係を直感的に把握することが可能になります。
def plot_animation(df, start_node, end_node):
# 開始ノードに一致する行を df から選択
df_start = df[df["start"] == start_node]
# 終了ノードに一致する行を df から選択
df_end = df[df["end"] == end_node]
## 基本的な地図を作成
# df のデータを地図上にプロット
# - 経度: "start_x"
# - 緯度は "start_y"
# - ズームレベル: 15
# - 幅: 1000
# - 高さ: 800
# - アニメーションフレーム: "id"
# - 地図スタイル: "carto-positron"
fig = px.scatter_mapbox(data_frame=df, lon="start_x", lat="start_y",
zoom=15, width=1000, height=800,
animation_frame="id", mapbox_style="carto-positron")
## ドライバーを追加
# 最初のデータセット(ドライバー)のマーカーサイズを 12 に設定
fig.data[0].marker = {"size":12}
## 開始点を追加
# df_startのデータを地図に追加
fig.add_trace(px.scatter_mapbox(data_frame=df_start,
lon="start_x", lat="start_y").data[0])
# 開始点のマーカーサイズを15、色を赤に設定
fig.data[1].marker = {"size":15, "color":"red"}
## 終了点を追加
# df_end のデータを地図に追加
fig.add_trace(px.scatter_mapbox(data_frame=df_end,
lon="start_x", lat="start_y").data[0])
# 終了点のマーカーサイズを15、色を緑に設定
fig.data[2].marker = {"size":15, "color":"green"}
## 経路を追加
# df のデータを使用して、地図上に経路を描画
fig.add_trace(px.line_mapbox(data_frame=df, lon="start_x", lat="start_y").data[0])
return fig
plot_animation(df, start_node, end_node)
4.2.12. ノード間の複数経路での移動シミュレーション
前のセクションでは、単一の経路でアニメーションを描画しましたが、次は、複数の経路でアニメーションを描画していきます。
まずは、複数のパスをリスト形式で引き渡し、アニメーション表示のためのデータフレームを返す関数を定義します。
# パスのリストを受け取り、アニメーション表示のためのデータフレームを生成する関数
def df_animation_multiple_path(G, lst_paths, parallel=True):
# 結果を格納するための空のデータフレームを初期化
df = pd.DataFrame()
# 各パスについて処理を実施
for path in lst_paths:
# 各種情報を格納するためのリストを初期化
lst_start, lst_end = [],[]
start_x, start_y = [],[]
end_x, end_y = [],[]
lst_length, lst_time = [],[]
# パスの各セグメントについて情報を抽出
for a,b in zip(path[:-1], path[1:]):
# 開始ノードと終了ノード
lst_start.append(a)
lst_end.append(b)
# セグメントの長さと所要時間
lst_length.append(round(G.edges[(a,b,0)]['length']))
lst_time.append(round(G.edges[(a,b,0)]['travel_time']))
# 開始ノードと終了ノードの座標
start_x.append(G.nodes[a]['x'])
start_y.append(G.nodes[a]['y'])
end_x.append(G.nodes[b]['x'])
end_y.append(G.nodes[b]['y'])
# 抽出した情報をもとにデータフレームを作成
tmp = pd.DataFrame(list(zip(lst_start, lst_end,
start_x, start_y,
end_x, end_y,
lst_length, lst_time)),
columns=["start", "end",
"start_x", "start_y", "end_x", "end_y",
"length", "travel_time"])
# 作成したデータフレームを結果に追加
df = pd.concat([df,tmp], ignore_index=(not parallel))
# ID列を追加してリセット
df = df.reset_index().rename(columns={"index":"id"})
return df
ここでは、特定の開始ノード start_node と終了ノード end_node をつなぐ2つの経路(最短時間の経路と最短距離の経路)それぞれについて、df_animation_multiple_path 関数でデータフレームを生成しています。
# 開始ノードと終了ノードを設定
first_node, last_node = start_node, end_node
# 複数のパスを含むリストを初期化
lst_paths = [path_time, path_length]
# パスの総数とノードの総数を表示
print(len(lst_paths), "パス,",
sum(len(i) for i in lst_paths), "ノード:",
first_node, "...", last_node)
# df_animation_multiple_path 関数を使用して、パスの情報からデータフレームを作成
df = df_animation_multiple_path(G, lst_paths, parallel=True)
# 作成したデータフレームの最後の5行を表示
df.tail()
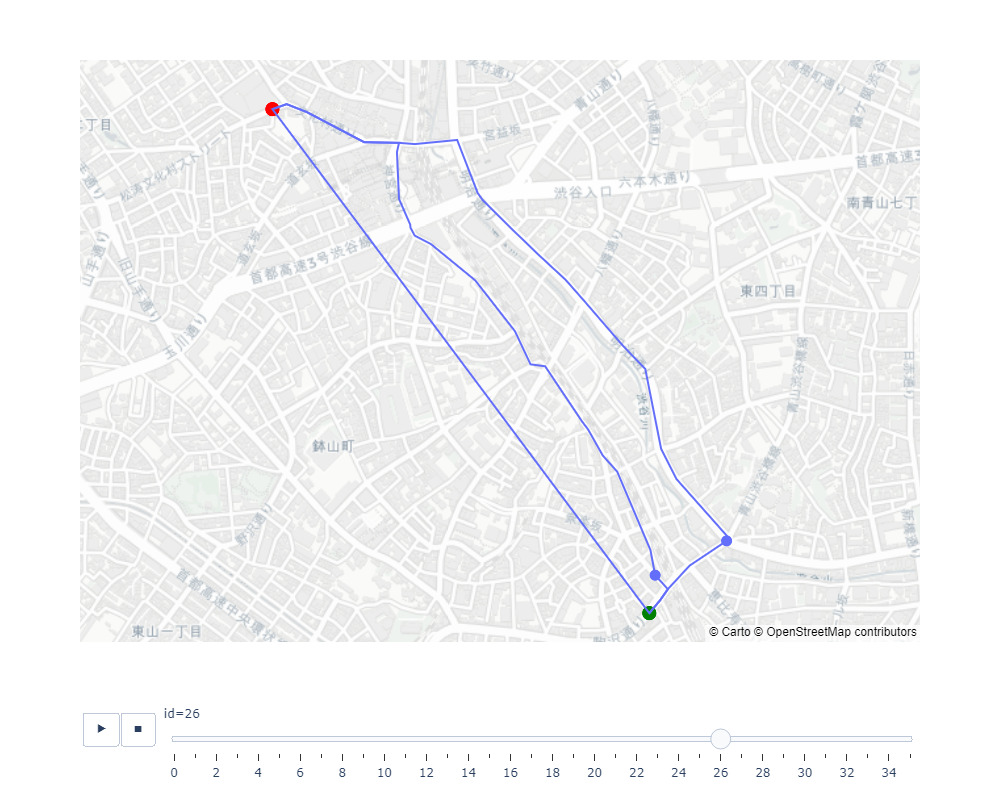
複数パスのアニメーションをプロットします。
plot_animation(df, first_node, last_node)
4.3. 前処理
4.3.1. 各場所の地理的位置と GeoDataFrames ノードの紐付け
次に GeoDataFrames を活用して、あるノードから別のノードへの最適なパスを見つける基本的な手法について紹介します。これは、複数の場所を効率的に訪れるためのルートを計算するための初歩的なステップとなります。
以下のような一般的な手順にしたがって処理を進めます。
- すべての位置間の最短パスコストを含む距離行列を生成
- この距離行列を基に初期解を構築
- 一連の反復プロセスを通じて解を改善
まず初めに今回使用するデータフレームを確認しておきます。
print(len(df))
df.head()
28

Pandas と OSMnx ライブラリの組み合わせを活用することで、データフレーム内の各位置に最も近いノード(グラフ上の点)を効率的に特定し、重複するノードを排除することができます。このプロセスは、地理的なデータの分析やネットワーク上での最適な経路計算において重要な役割を果たします。
具体的なやり方としては、データフレームに含まれる各地点に対して、OSMnx ライブラリを使用して道路ネットワークグラフ上の最も近いノードを見つけ出します。これにより、実際の地理的位置とグラフ上のノードとの間の関連付けが可能になります。
さらに、Pandas の機能を用いて重複するノードを削除します。これにより、データの冗長性を排除し、分析の精度を高めることができます。
## 各位置に対応するノードを取得
# DataFrame 'df' の 'y'(緯度)と 'x'(経度)の列を使用して、
# lambda 関数を適用し、各位置に最も近いノードを見つける
# ox.distance.nearest_nodes() 関数は、指定された緯度と経度に基づいて最も近いノードの ID を返す
dtf["node"] = dtf[["y","x"]].apply(lambda x: ox.distance.nearest_nodes(G,x[1],x[0]), axis=1)
# 重複するノードを削除し、最初に出現するもののみを保持
dtf = dtf.drop_duplicates("node", keep='first')
# DataFrame の最初の数行を表示
dtf.head()
4.3.2. すべての位置間の距離行列の計算
最適化モデルを適用する上での重要となる初期ステップは、データセット内のすべての位置間の距離行列を計算することです。このプロセスでは、各ノード間の最短パスの距離をすべて特定していきます。
これを行うため、NetworkX ライブラリを使用して、DataFrame 内のノード間の距離行列を効率的に計算していきます。計算された距離行列は、Pandas DataFrame に整理され、後続の分析やモデル適用のための基礎データとして利用されます。
## 距離計算関数の定義
# 2つのノード間の最短経路の長さ(移動時間)を計算する関数
def f(a,b):
try:
d = nx.shortest_path_length(G, source=a, target=b,
method='dijkstra', weight='travel_time')
except:
d = np.nan
return d
## 関数の適用
# データフレームの node 列の各ノード間で関数 f を適用し、距離行列を計算
# np.asarray を使用して、リスト内包表記で計算された距離行列を NumPy 配列に変換
distance_matrix = np.asarray([[f(a,b) for b in dtf["node"].tolist()]
for a in dtf["node"].tolist()])
# 距離行列を Pandas データフレームに変換
# 列名とインデックスには node 列の値を使用
distance_matrix = pd.DataFrame(distance_matrix,
columns=dtf["node"].values,
index=dtf["node"].values)
# DataFrame の最初の数行を表示
distance_matrix.head()
4.3.3. 距離行列のヒートマップ作成
データセット内に NaN、0、および無限大 (Inf) といった異常なデータが存在すると、その後の計算などに影響が出る可能性があるため、これらのデータが存在していないか事前に確認することは非常に重要です。
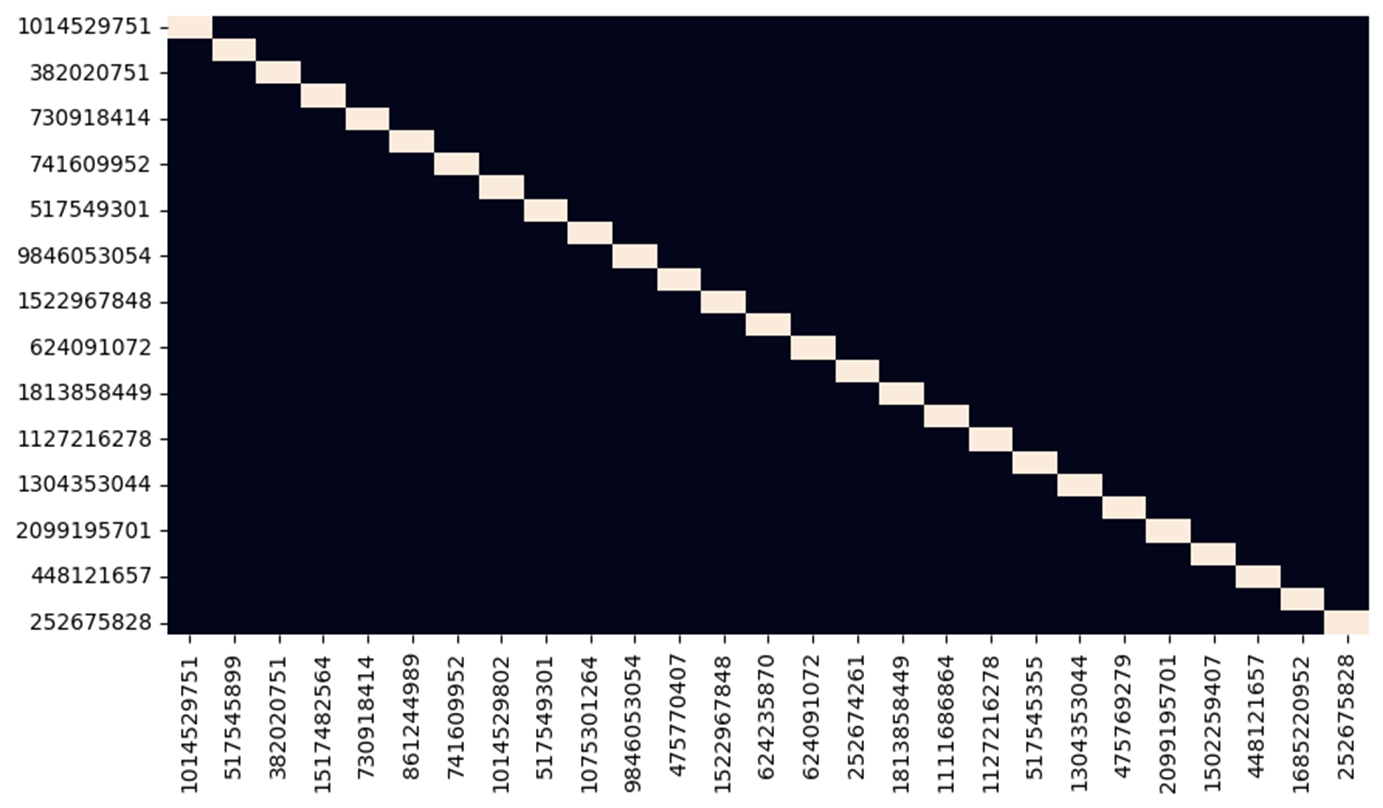
Seaborn ライブラリを使用して距離行列のヒートマップを作成し、さらに Matplotlib を用いてこうしたデータを可視化していきます。ヒートマップは、データのパターンや異常値を直感的に理解するのに役立ちます。
ヒートマップを作成することで、距離行列内の各要素間の距離の大きさを色の濃淡で表現し、データの全体的な構造や特定の特徴を一目で把握することができます。特に、大規模なデータセットや複雑な地理的関係を持つ場合に、この視覚化手法は非常に有効です。
# 距離行列のコピーを作成してヒートマップ用に使用
heatmap = distance_matrix.copy()
# ヒートマップの各セルの値を設定
for col in heatmap.columns:
heatmap[col] = heatmap[col].apply(
lambda x: 0.3 if pd.isnull(x) # NaN の場合は 0.3(紫色)
else (0.7 if np.isinf(x) # 無限大の場合は 0.7(オレンジ色)
else (0 if x!=0 else 1) )) # 0 の場合は 1(白色)、それ以外は 0
# Matplotlib で図のサイズを設定し、サブプロットを作成
fig, ax = plt.subplots(figsize=(10,5))
# ヒートマップを描画
# - vmin, vmax: 色の範囲を 0 から 1 に設定
# - カラーバー: 非表示
sns.heatmap(heatmap, vmin=0, vmax=1, cbar=False, ax=ax)
# ヒートマップを表示
plt.show()
4.3.4. 異常値の置き換え
幸いにも前の手順で行ったヒートマップ表示では、対角線上に 0 が存在しており、NaN や無限大 (Inf) は存在しておらず、異常なデータは存在していないことが確認できました。
異常値が存在している場合、使用されるルーティングモデルに大きな影響を与えるため、細心の注意を払う必要があります。
異常値はその行の平均距離に置き換えるのが一般的です。この方法により、データセットの整合性を保ちながら、より実用的な解析を行うことが可能になります。
この異常値の置き換えは、データの品質を向上させ、最終的なルーティングモデルの精度を高める重要なステップです。Pandas を用いることで、この処理を効率的かつ正確に行うことができます。
# 欠損値を行の平均値で埋める
# 1. 距離行列を転置して(.T)、各列(元の行)の NaN をその列の平均値で埋める(fillna)
# 2. 再び転置して元の形に戻す
distance_matrix = distance_matrix.T.fillna(distance_matrix.mean(axis=1)).T
distance_matrix.head()
4.4. 巡回セールスマン問題の解決
4.4.1. 初期パラメータの設定
最適なルートを見つけるためには、まずドライバーの数と訪問すべきノードのリストを定義する必要があります。この今回の例では、1人のドライバーが複数のノードを訪れるシナリオを想定しています。
まずは、データフレームからノードのリストを取得し、開始ノードと訪問する場所の総数を確認します。これが、ルート最適化や配送計画を行う際の基礎となります。
# ドライバー数を設定
drivers = 1
# DataFrame 'df' から 'node' 列の値をリストとして取得
lst_nodes = dtf["node"].tolist()
# 開始ノード、総訪問地点、使用するドライバーの数を表示
# 総訪問地点は、リスト 'lst_nodes' の長さから 1 (開始ノード) を引いたもの
print("開始ノード:", start_node, "| 総訪問地点:", len(lst_nodes)-1, "| ドライバー数:", drivers)
開始ノード: 1014529751 | 総訪問地点: 26 | ドライバー数: 1
4.4.2. インデックスマネージャーとルーティングモデルの作成
Google の OR-Tools ライブラリは、線形計画法をはじめとする最適化問題を解決するためのツールです。このライブラリを使用して、ノードのインデックスを管理するインデックスマネージャーと、ルーティングモデルを定義します。
OR-Tools は、矛盾からの節学習 (Conflict-Driven Clause Learning, CDCL) などの高度なテクニックを利用して、効率的な解決策を見つけ出します。
# ルーティング問題のインデックスマネージャーを作成
# - len(lst_nodes): 訪問するノードの総数
# - drivers: 使用するドライバーの数
# - lst_nodes.index(start_node): 開始ノードのインデックス
manager = pywrapcp.RoutingIndexManager(
len(lst_nodes),
drivers,
lst_nodes.index(start_node))
# インデックスマネージャーを基にルーティングモデルを作成
model = pywrapcp.RoutingModel(manager)
4.4.3. ルーティングモデルへの距離コストの評価関数の設定
ルーティングモデルには、各ノード間の距離コストを評価する評価関数を設定します。この関数は、ルートの総距離を計算し、最適なルート選択に重要な役割を果たします。
# 2つのインデックス (from_index と to_index) を受け取り、
# distance_matrix から対応する距離を返す
def get_distance(from_index, to_index):
return distance_matrix.iloc[from_index,to_index]
# モデルに距離取得関数を登録
distance = model.RegisterTransitCallback(get_distance)
# すべての車両に対して距離コスト評価関数を設定
model.SetArcCostEvaluatorOfAllVehicles(distance)
4.4.4. 最初の解の戦略の設定
最後に、ルーティング問題の解決に向けた検索戦略を設定します。この戦略は、問題の初期解を見つけるためのアプローチを定義し、最終的な解決策に至る過程を効率化します。
# デフォルトのルーティング検索パラメータを取得
parameters = pywrapcp.DefaultRoutingSearchParameters()
# 最初の解を生成する戦略を設定
# parameters.first_solution_strategy に
# 最もコストの低いアーク(経路のセグメント)を選択する戦略である PATH_CHEAPEST_ARC 戦略を設定
parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)
4.4.5. 問題の解決および結果の出力
計算されたルーティング問題の解を解析し、各ドライバーのルート、距離、訪問ノード数を表示します。
# 設定されたパラメータでルーティング問題を解く
solution = model.SolveWithParameters(parameters)
# ドライバー#0 の開始インデックスを取得
index = model.Start(0)
print('ドライバーのルート:')
route_idx, route_distance = [], 0
# ルートの各ノードを走査
while not model.IsEnd(index):
# 現在のインデックスに対応するノードをリストに追加
route_idx.append( manager.IndexToNode(index) )
previous_index = index
# 次のインデックスを取得
index = solution.Value( model.NextVar(index) )
# 距離を更新
try:
# 距離を取得し、ルートの総距離に加算
route_distance += get_distance(previous_index, index)
except:
# エラーが発生した場合は、距離を取得
route_distance += model.GetArcCostForVehicle(
from_index=previous_index,
to_index=index,
vehicle=0)
# ルートのインデックス、総移動距離、訪問ノード数を表示
print(route_idx)
print(f'総移動距離: {round(route_distance/1000,2)} km')
print(f'訪問ノード: {len(route_idx)}')
ドライバーのルート:
[0, 26, 25, 24, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
総移動距離: 5.88 km
訪問ノード: 27
4.4.6. 問題の解として得られたノードを表示
計算されたルートをノードのリストに変換します。
# ドライバーのルート(ノード)を表示
print("ドライバーのルート(ノード):")
# route_idx に含まれるインデックスに対応するノードを lst_nodes から取得し、
# lst_route というリストに格納
lst_route = [lst_nodes[i] for i in route_idx]
# lst_route を表示
# これにより、ドライバーが訪れるノードの順序が表示される
print(lst_route)
ドライバーのルート(ノード):
[1014529751, 252675828, 1685220952, 448121657, 1502259407, 2099195701, 475769279, 1304353044, 517545355, 1127216278, 1111686864, 1813858449, 252674261, 624091072, 624235870, 1522967848, 475770407, 9846053054, 1075301264, 517549301, 1014529802, 741609952, 861244989, 730918414, 1517482564, 382020751, 517545899]
4.4.7. 地図上へのルートの描画
各ドライバーのルートを地図上に描画し、視覚化します。
# ノード間の経路を取得する関数
def get_path_between_nodes(lst_route):
lst_paths = []
for i in range(len(lst_route)):
try:
# 現在のノードと次のノードを取得
a,b = lst_route[i], lst_route[i+1]
except:
# 次のノードがない場合はループを終了
break
try:
# グラフ G 上でノード a からノード b までの最短経路を計算
# ダイクストラ法を使用し、重みは 'travel_time'(移動時間)で計算
path = nx.shortest_path(G, source=a, target=b,
method='dijkstra', weight='travel_time')
# 経路が存在する場合(長さが 1 より大きい場合)、リストに追加
if len(path) > 1:
lst_paths.append(path)
except:
# 経路が見つからない場合は次のループへ
continue
return lst_paths
# ルート内の各ノード間の経路を取得
lst_paths = get_path_between_nodes(lst_route)
# Folium 地図上に経路をプロット
map_ = plot_map(dtf, y="y", x="x", start=start, zoom=12,
tiles="cartodbpositron", popup="id",
color="base", lst_colors=["blue","red"])
for path in lst_paths:
ox.plot_route_folium(G, route=path, route_map=map_, color="blue", weight=1)
map_
アニメーションでも表示してみます。
# animation
first_node, last_node = lst_paths[0][0], lst_paths[-1][-1]
print(len(lst_paths), "パス,",
sum(len(i) for i in lst_paths), "ノード:",
first_node, "...", last_node)
df = df_animation_multiple_path(G, lst_paths, parallel=False)
plot_animation(df, first_node, last_node)
4.5. 運搬経路問題の解決
4.5.1. 運搬経路問題の制約の設定
実際の商用環境では、多様な制約が配車経路問題に影響を与えることがあります。制約は状況によって変わってきますが、以下に一例を示します。
-
容量制約:
- 各車両には限られた積載量があり、この制約を超えることはできない。
- 車両が運べる商品の量や人数に制限がある状況に対応する。
-
時間窓制約:
- 顧客への訪問には特定の時間枠(時間窓)が設定されている場合がある。
- 顧客が特定の時間帯にのみサービスを受け入れる状況を反映している。
-
距離または時間の制約:
- ルートの総距離や総所要時間に制限を設けることがある。
- 運転手の労働時間の制限や燃料の消費を考慮した場合に適用される。
-
ルート数の制約:
- 利用可能な車両の数によってルートの数が制限されることがある。
-
顧客サービス制約:
- 特定の顧客には特定の車両が必要な場合や、特定のスキルを持つドライバーが必要な場合がある。
-
多倉庫制約:
- 複数の配送センターや倉庫からの配送を考慮する必要がある場合です。
-
ルートの継続性:
- 各ルートは同一の車両によって連続して完了される必要がある。
-
利益の最大化:
- 必ずしもすべてのノードを訪問する必要はなく、目的は収集された利益の合計を最大化することである。
今回はドライバーの積載量と走行可能距離に制限を設けます。
ルーティング問題を解くための初期パラメータを設定し、これらを制約条件として適用します。これにより、実際の商用環境における複雑な要件を満たすルートの計画が可能になります。
## 初期パラメータの設定
# 使用するドライバーの数を設定
drivers = 3
# 各ドライバーの積載量を設定(ここではすべてのドライバーで 10 と設定)
driver_capacities = [10,10,10]
# 各ノードの需要を設定
# 開始ノードの需要は 0、他のノードの需要は 1 と設定
# lst_nodes の長さから1を引いた数だけ 1 をリストに追加
demands = [0] + [1]*(len(lst_nodes)-1)
# 各ドライバーの最大移動距離を設定(ここでは 1000 と設定)
max_distance = 1000
4.5.2. マネージャーとモデルの作成および距離関数の追加
運搬経路問題を解決するには、効率的なルーティングモデルの作成が欠かせません。このプロセスには、マネージャーの作成と距離関数の追加が含まれます。
まずは、OR-Tools ライブラリを使用して、ルーティング問題のためのモデルを作成します。このモデルは、複数の制約条件を考慮した上で、最適なルートを計算するための基盤を提供します。
## モデルの作成
# ルーティング問題のインデックスマネージャーを作成
# - len(lst_nodes): は訪問するノードの総数
# - drivers: 使用するドライバーの数
# - lst_nodes.index(start_node): 開始ノードのインデックス
manager = pywrapcp.RoutingIndexManager(len(lst_nodes), drivers, lst_nodes.index(start_node))
# インデックスマネージャーを基にルーティングモデルを作成
model = pywrapcp.RoutingModel(manager)
## 距離(コスト)の追加
# 2つのインデックス間の距離を返す関数を定義
def get_distance(from_index, to_index):
return distance_matrix.iloc[from_index,to_index]
# モデルに距離取得関数を登録
distance = model.RegisterTransitCallback(get_distance)
# すべての車両に対して距離コスト評価関数を設定
model.SetArcCostEvaluatorOfAllVehicles(distance)
4.5.3. 制約の追加
次に OR-Tools の ルーティングライブラリを使用して、容量制約と距離制約を含むルーティング問題を解決します。
# 需要(荷物の量やサービスの需要など)を取得する関数を定義
# - from_index: 地点のインデックス
# - demands: 各地点の需要を格納したリストまたは配列
def get_demand(from_index):
return demands[from_index]
# モデルに需要のコールバック関数を登録
# この関数は、各地点の需要をモデルに提供する
demand = model.RegisterUnaryTransitCallback(get_demand)
# 車両の容量制約をモデルに追加
# - demand: 需要のコールバック関数
# - slack_max=0: スラック(余裕)の最大値を0に設定(厳密な容量制約)
# - vehicle_capacities: 各車両の容量を格納したリストまたは配列
# - fix_start_cumul_to_zero=True: 累積量の開始値を0に固定
# - name='Capacity': この制約の名前
model.AddDimensionWithVehicleCapacity(demand, slack_max=0,
vehicle_capacities=driver_capacities,
fix_start_cumul_to_zero=True,
name='Capacity')
# 距離制約をモデルに追加
# - distance: 距離のコールバック関数
# - slack_max=0: スラックの最大値を0に設定
# - capacity=max_distance: 距離の最大値
# - fix_start_cumul_to_zero=True: 累積量の開始値を 0 に固定
# - name=name: この制約の名前
name = 'Distance'
model.AddDimension(distance, slack_max=0, capacity=max_distance,
fix_start_cumul_to_zero=True, name=name)
# 距離制約のグローバルスパンコスト係数を設定
# これにより、全体の距離を最小化するようにルートが最適化される
distance_dimension = model.GetDimensionOrDie(name)
distance_dimension.SetGlobalSpanCostCoefficient(100)
# ルーティングの検索パラメータを設定
parameters = pywrapcp.DefaultRoutingSearchParameters()
# 最初の解の戦略として「最も安いアークを選択」を設定
# これは、最もコストの低い経路を最初に選択する戦略
parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)
4.5.4. 問題の解決および結果の出力
問題を解決した後、OR-Tools を使用して得られた解を詳細に分析します。各ドライバーのルート、距離、積載量を表示し、全体の距離と積載量を集計します。これにより、最適なルートの選択と効率的な配送計画が可能になります。
# モデルを解き、解を取得
solution = model.SolveWithParameters(parameters)
# 各ドライバーのルート、総距離、総積載量を格納するための変数を初期化
dic_routes_idx, total_distance, total_load = {}, 0, 0
# 各ドライバーについてループを行う
for driver in range(drivers):
print(f'ドライバー#{driver}のルート:')
# ドライバーのルートの開始地点を取得
index = model.Start(driver)
route_idx, route_distance, route_load = [], 0, 0
# ルートの終点に到達するまでループを続ける
while not model.IsEnd(index):
node_index = manager.IndexToNode(index)
route_idx.append( manager.IndexToNode(index) )
previous_index = index
index = solution.Value( model.NextVar(index) )
# 距離を更新
try:
route_distance += get_distance(previous_index, index)
except:
route_distance += model.GetArcCostForVehicle(
from_index=previous_index, to_index=index, vehicle=driver)
# 積載量を更新
route_load += demands[node_index]
# ルートの終点を追加
route_idx.append( manager.IndexToNode(index) )
print(route_idx)
# ドライバーごとのルート情報を辞書に格納
dic_routes_idx[driver] = route_idx
# ドライバーごとの距離と積載量を表示
print(f'距離: {round(route_distance/1000,2)} km')
print(f'積載数: {round(route_load,2)}', "\n")
# 総距離と総積載量を更新
total_distance += route_distance
total_load += route_load
# 全ドライバーの総距離と総積載量を表示
print(f'総移動距離: {round(total_distance/1000,2)} km')
print(f'総積載量: {total_load}')
ドライバー#0のルート:
[0, 6, 5, 4, 3, 2, 1, 0]
距離: 1.54 km
積載数: 6ドライバー#1のルート:
[0, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 0]
距離: 1.78 km
積載数: 10ドライバー#2のルート:
[0, 26, 25, 24, 23, 22, 21, 20, 19, 18, 17, 0]
距離: 2.33 km
積載数: 10総移動距離: 5.65 km
総積載量: 26
4.5.5. 問題の解として得られたノードを表示
インデックス形式の計算されたルートをノード(地点)のリストに変換し、それを表示します。これにより、ルートの具体的な経路が明確になります。
# インデックスからノード(地点)への変換を行うための辞書を初期化
dic_route = {}
# 以前に計算された各ドライバーのルート(インデックス形式)をループ
for k,v in dic_routes_idx.items():
print(f"ドライバー#{k}のルート(ノード):")
# ルートのインデックスを実際のノード(地点)に変換
# - lst_nodes: 各インデックスに対応するノード(地点)を格納したリスト
# - v: ドライバーのルート(インデックス形式)
dic_route[k] = [lst_nodes[i] for i in v]
# 変換されたルート(ノード形式)を表示
print(dic_route[k], "\n")
ドライバー#0のルート(ノード):
[1014529751, 741609952, 861244989, 730918414, 1517482564, 382020751, 517545899, 1014529751]ドライバー#1のルート(ノード):
[1014529751, 1813858449, 252674261, 624091072, 624235870, 1522967848, 475770407, 9846053054, 1075301264, 517549301, 1014529802, 1014529751]ドライバー#2のルート(ノード):
[1014529751, 252675828, 1685220952, 448121657, 1502259407, 2099195701, 475769279, 1304353044, 517545355, 1127216278, 1111686864, 1014529751]
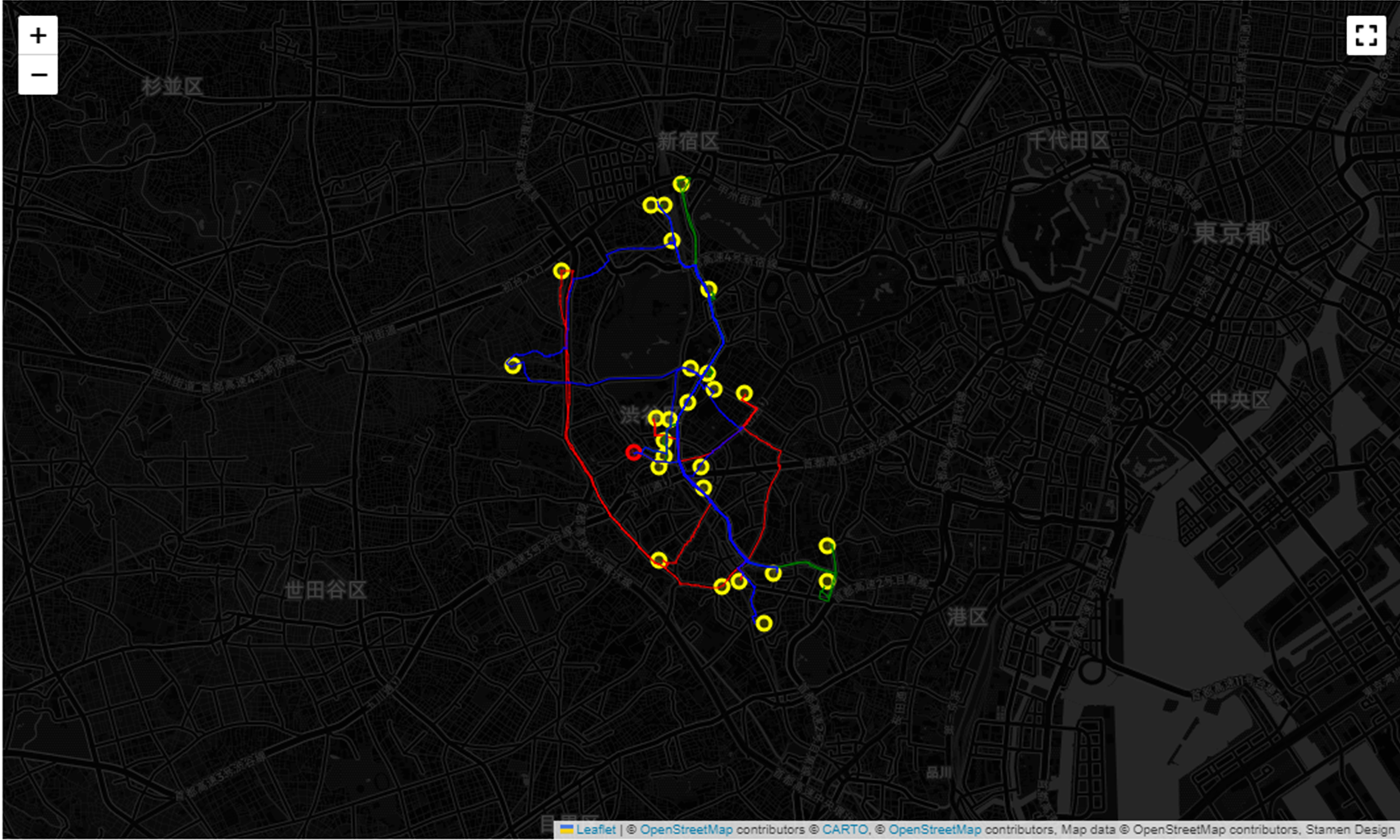
4.5.6. 地図上へのルートの描画
各ドライバーのルートを地図上に描画し、視覚的に表示します。これにより、ルートの地理的な概要を直感的に把握できます。
# 各ドライバーのルートに対して、ノード間の具体的なパス(経路)を取得
# - get_path_between_nodes: ノード間のパスを取得する関数
# - dic_route: ドライバーごとのルート(ノード形式)を格納した辞書
dic_paths = {k:get_path_between_nodes(v) for k,v in dic_route.items()}
len(dic_paths)
map_ = plot_map(dtf, y="y", x="x", start=start, zoom=11,
tiles="cartodbpositron", popup="id",
color="base", lst_colors=["yellow","red"])
# 地図上に各ドライバーのルートを描画するための色のリストを定義
lst_colors = ["red","green","blue"]
# 各ドライバーのパス(経路)を地図上に描画
for k, v in dic_paths.items():
for path in v:
# Folium 地図上にルートを描画
# - G: 地図のグラフ
# - route: 描画するルート
# - route_map: 描画対象のFolium地図
# - color: ルートの色
# - weight: ルートの線の太さ
ox.plot_route_folium(G, route=path, route_map=map_, color=lst_colors[k], weight=1)
# 地図を表示
map_
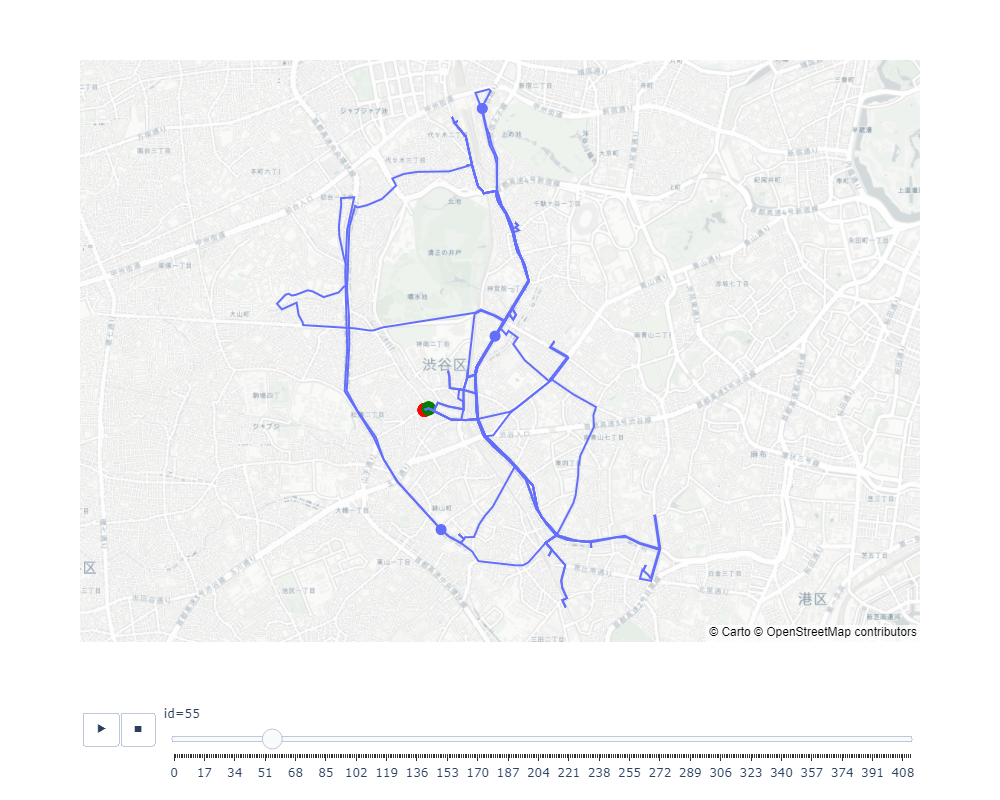
4.5.7. アニメーションの描画
最後に、地理的なデータを含むデータフレームを使用して、動的な地図上にアニメーションを描画します。これにより、ルートの動的な側面を視覚的に表現し、より魅力的なデータプレゼンテーションが可能になります。
# 空のデータフレームを初期化
df = pd.DataFrame()
# 各ドライバーのパスについて処理を行う
for driver,lst_paths in dic_paths.items():
# 各パスのデータを非並行処理で収集し、一時的なデータフレームとして取得
tmp = df_animation_multiple_path(G, lst_paths, parallel=False)
# 一時的なデータフレームを既存のデータフレームに縦方向に結合
df = pd.concat([df,tmp], axis=0)
# 最初のノードと最後のノードを取得
first_node, last_node = lst_paths[0][0], lst_paths[-1][-1]
# データフレームを使用してアニメーションを描画し、地図を表示
plot_animation(df, first_node, last_node)
5. 総括
この記事では、Pythonを活用したルート最適化の手法について詳しく解説しました。ルート最適化は、効率的な配送計画や交通流の管理に不可欠なプロセスです。
地理データセットの視覚化とネットワークグラフの構築
まず、地理データセットを地図上で視覚化し、ネットワークグラフを構築する基本的な手順を学びました。このステップは、地理的な情報を理解し、ルート計画の基礎を築く上で重要です。
巡回セールスマン問題と車両ルーティング問題の解決
巡回セールスマン問題を用いて、単一のドライバーにとっての最短ルートを見つける方法を紹介しました。また、車両ルーティング問題を使用して、複数のドライバーにとっての最適なルートを計算する方法も探求しました。これらの問題は、実際のビジネスシナリオにおける複雑なルーティング要件を解決するために重要です。
地理空間データの活用
さらに、地理空間データを活用してインタラクティブなプロットやアニメーションを作成する方法についても説明しました。これにより、ルートの動的な側面を視覚的に捉え、より深い洞察を得ることができます。
まとめ
このチュートリアルを通じて、Python を用いたルート最適化の基本から応用までを網羅的に学ぶことができました。地理データの視覚化から始まり、複雑なルーティング問題の解決、そして動的なデータのプレゼンテーションに至るまで、これらの技術は多くの業界での効率的な意思決定に貢献します。
6. 参考文献
- "Modern Route Optimization with Python", https://towardsdatascience.com/modern-route-optimization-with-python-fea87d34288b
- "DataScience_ArtificialIntelligence_Utils/machine_learning/example_route_optimization.ipynb at master · mdipietro09/DataScience_ArtificialIntelligence_Utils", https://github.com/mdipietro09/DataScience_ArtificialIntelligence_Utils/blob/master/machine_learning/example_route_optimization.ipynb
- "Starbucks Locations Worldwide", https://www.kaggle.com/starbucks/store-locations
- "巡回セールスマン問題 - Wikipedia", https://ja.wikipedia.org/wiki/%E5%B7%A1%E5%9B%9E%E3%82%BB%E3%83%BC%E3%83%AB%E3%82%B9%E3%83%9E%E3%83%B3%E5%95%8F%E9%A1%8C
- "Vehicle routing problem - Wikipedia", https://en.wikipedia.org/wiki/Vehicle_routing_problem