現代においてデータは資産であり、そのデータを活用して分析を行うことは、戦略的な意思決定を行う上で必要不可欠なものであると言えます。この記事では、一般的な分析シナリオを取り上げ、それぞれの手法と Python での実装例について解説していきます。
ここでは、以下の分析シナリオについて取り扱っていきます。
- 予兆発見型
- 異常検出型
a. 不正検出型
b. 外れ値検出型 - 予測・制御型
a. 収益シミュレーション型
b. リスク・シミュレーション型
c. 最適化型
d. リスクヘッジ型 - ターゲティング型
- 与信管理型
- 評価・要因分析
- コンテクスト・アウェアネス型
- プロセス・トレース型
1. 予兆発見型(Early Warning System)
予兆発見型分析は、将来の問題や機会を早期に識別することを目的としています。これは、データのパターンや傾向を分析して、異常や重要な変化を検出することにより行われます。
利用例:
利用例としては、機械の故障予測、健康リスクの警告、市場の変動予測などがあります。
分析手法:
時系列データやセンサーデータの異常パターンをモデル化し、異常が発生する前に予兆を検出するために、機械学習アルゴリズムや時系列解析を使用します。
その代表的な手法の一つとして ARIMA(自己回帰積分移動平均)モデルがあります。
$$
Y_t = c + \epsilon_t + \sum_{i=1}^{p} \phi_i Y_{t-i} + \sum_{i=1}^{q} \theta_i \epsilon_{t-i}
$$
$Y_t$:時刻 $t$ での観測値
$c$:定数
$\phi$, $\theta$:モデルのパラメータ
$\epsilon_t$:誤差項
Python 実装
予兆発見型の分析シナリオである ARIMA(自己回帰積分移動平均)モデルを Python で実装し、その結果を可視化する例を示します。
以下のコードは、ARIMA モデルを使用して架空の時系列データに対する予測を行い、その結果をプロットしています。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import itertools
import statsmodels.api as sm
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_predict
# 架空の時系列データ生成
np.random.seed(0)
data = np.random.randn(100).cumsum() + 100 # ランダムウォークデータ
# パラメータ候補の設定
p = d = q = range(0, 3)
pdq = list(itertools.product(p, d, q))
# AICを最小化する最適なパラメータの初期値設定
best_aic = float("inf")
best_params = None
# パラメータチューニングのループ
for params in pdq:
try:
model = ARIMA(data, order=params)
results = model.fit()
aic = results.aic
if aic < best_aic:
best_aic = aic
best_params = params
except:
continue
# 最適なパラメータでARIMAモデルを訓練
best_model = ARIMA(data, order=best_params)
# ARIMAモデルの適用
best_results = best_model.fit()
# 予測
forecast = best_results.get_forecast(steps=10)
forecast_mean = forecast.predicted_mean
confidence_intervals = forecast.conf_int()
# 可視化
plt.figure(figsize=(12, 6))
plt.plot(data, label='観測値')
plt.plot(np.arange(len(data), len(data) + 10), forecast_mean, label='予測')
plt.fill_between(np.arange(len(data), len(data) + 10), confidence_intervals[:, 0], confidence_intervals[:, 1], color='pink', alpha=0.3)
plt.title('ARIMA モデルによる予測')
plt.xlabel('時間')
plt.ylabel('値')
plt.legend()
plt.show()
2. 異常検出型
a. 不正検出型(Fraud Detection)
不正検出は、通常のパターンから逸脱する活動を識別し、詐欺や不正行為を発見することを目的としています。
利用例:
利用例としては、金融取引、クレジットカードの使用、保険請求などの不正利用の検出などがあります。
分析手法:
不正検出では、分類問題として扱われることが多く、一般的にロジスティック回帰、サポートベクターマシン、深層学習などの不正検出モデルが利用されます。
ロジスティック回帰の場合、以下のような数式で表されます。
$$
P(Y=1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X_1 + \cdots + \beta_n X_n)}}
$$
$P(Y=1|X)$:不正である確率
$X$:特徴量
$\beta$:モデルのパラメータ
Python 実装
不正検出型の分析シナリオであるロジスティック回帰を Python で実装し、その結果を可視化する例を示します。
この例では、架空のデータセットを使用してロジスティック回帰モデルをトレーニングし、特定の特徴に基づいて不正行為を検出します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
# 架空のデータセット生成
np.random.seed(0)
X = np.random.randn(200, 2)
y = np.random.randint(0, 2, 200) # 0 は正常、1 は不正
# データセットをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# ロジスティック回帰モデルのトレーニング
model = LogisticRegression()
model.fit(X_train, y_train)
# テストデータに対する予測
y_pred = model.predict(X_test)
# モデルの評価
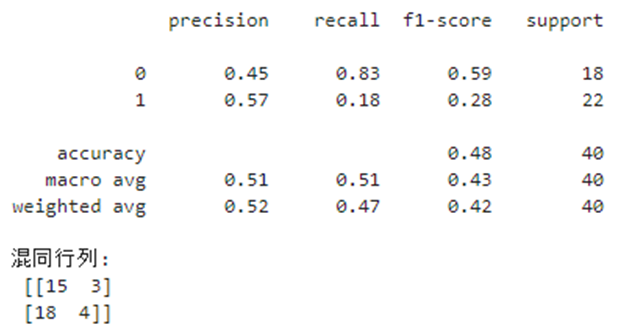
print(classification_report(y_test, y_pred))
print("混同行列:\n", confusion_matrix(y_test, y_pred))
# 可視化
plt.figure(figsize=(10, 6))
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_pred, cmap='coolwarm', edgecolor='k', s=40)
plt.title('ロジスティック回帰を用いた不正検出')
plt.xlabel('特徴量 1')
plt.ylabel('特徴量 2')
plt.show()

b. 外れ値検出型(Outlier Detection)
外れ値検出は、データセット内の異常な値やパターンを識別することを目的としています。
利用例:
外れ値検出は、データの品質を保証したり、重要な異常を見つけるために使用されます。前処理のデータクリーニングで外れ値除去を行う際に利用されたりもします。
分析手法:
外れ値検出では、データの分布からの逸脱を測定します。
Z スコアや IQR 法(四分位範囲法)、箱ひげ図などの「統計的手法」、または「クラスタリング」が利用されます。「統計的手法」は数値データに対して効果的であり、「クラスタリング」はより複雑なデータ構造やパターンを持つデータセットに適しているため、データセットや状況に応じて使い分けたり、組み合わせながら分析を行います。
Z スコアの場合は以下のようになります。
$$
Z = \frac{X - \mu}{\sigma}
$$
$X$:観測値
$\mu$:平均
$\sigma$:標準偏差
Python 実装:
ランダムに生成されたデータセットを使用し、Z スコアを計算して外れ値を識別します。外れ値は、通常、Z スコアが ±2.5 以上の値として定義されますが、この閾値は状況に応じて調整することができます。
import numpy as np
import matplotlib.pyplot as plt
# ランダムデータの生成
np.random.seed(0)
data = np.random.normal(0, 1, 100)
# Zスコアの計算
mean = np.mean(data)
std = np.std(data)
z_scores = (data - mean) / std
# 外れ値の識別
outliers = np.where(np.abs(z_scores) > 2.5)
# 可視化
plt.figure(figsize=(10, 6))
plt.plot(data, 'b.', label='データポイント')
plt.plot(outliers[0], data[outliers], 'ro', label='外れ値')
plt.axhline(y=mean + 2.5*std, color='g', linestyle='--', label='上限')
plt.axhline(y=mean - 2.5*std, color='g', linestyle='--', label='下限')
plt.title("Z スコアを用いた外れ値検出")
plt.xlabel("インデックス")
plt.ylabel("データ値")
plt.legend()
plt.show()
3. 予測・制御型
a. 収益シミュレーション型(Revenue Simulation)
収益シミュレーションは、将来の収益を予測し、ビジネス戦略や計画を策定する際に役立つ手法です。
利用例:
市場のトレンド、顧客の行動、経済状況などの要因を考慮したうえで、投資ポートフォリオの将来の収益を予測し、戦略を計画するといったことができます。
分析手法:
収益予測では、回帰分析、モンテカルロシミュレーション、金融モデル、シナリオ分析などがあり、目的や用途に応じて使い分けます。
関係性を特定するには回帰分析が適しています。
$$
Y = \beta_0 + \beta_1 X_1 + \cdots + \beta_n X_n + \epsilon
$$
$Y$:収益
$X$:予測因子
$\beta$:パラメータ
$\epsilon$:誤差項
Python 実装
収益シミュレーション型の分析シナリオにおける回帰分析を Python で実装し、その結果を可視化する例を示します。この例では、架空のデータセットを使用して、線形回帰モデルで分析を行い、特定の特徴に基づいて収益を予測します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 架空のデータセット生成
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# データセットをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 線形回帰モデルのトレーニング
model = LinearRegression()
model.fit(X_train, y_train)
# テストデータに対する予測
y_pred = model.predict(X_test)
# モデルの評価
mse = mean_squared_error(y_test, y_pred)
print("平均二乗誤差:", mse)
# 可視化
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='データ')
plt.plot(X_test, y_pred, color='red', label='線形回帰')
plt.title('線形回帰を用いた収益シミュレーション')
plt.xlabel('特徴')
plt.ylabel('収益')
plt.legend()
plt.show()
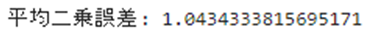
b. リスク・シミュレーション型(Risk Simulation)
リスクシミュレーションは、ビジネスやプロジェクトに関連するリスクを評価し、それらの影響をシミュレートすることを目的としています。
利用例:
一例として、プロジェクトのリスクを評価し、リスク管理戦略を策定する際に使うといった利用法が挙げられます。
分析手法:
リスク評価では、VaR (Value at Risk) やモンテカルロシミュレーション、ストレステスト、リスクアセスメントなどが用いられ、それぞれの特性に応じて組み合わせて利用されることが多いです。
このうち、金額的なリスク評価に強く、金融機関や投資ポートフォリオのリスク管理に広く用いられている VaR の場合は以下のようになります。
$$
P(L > VaR_\alpha) = \alpha
$$
$L$:損失
$VaR_\alpha$:特定の確率 $\alpha$ での最大損失
Python 実装:
この例では、架空の投資ポートフォリオのリターンをシミュレートし、その VaR (Value at Risk) を計算し、結果をヒストグラムで可視化します。
import numpy as np
import matplotlib.pyplot as plt
# ポートフォリオリターンのシミュレーション
np.random.seed(0)
num_days = 252 # 1年の取引日数
mean_return = 0.001 # 1日あたりの平均リターン
volatility = 0.02 # ボラティリティ(標準偏差)
# 日々のリターンをシミュレート
daily_returns = np.random.normal(mean_return, volatility, num_days)
# VaR の計算(信頼区間 95%)
VaR_95 = np.percentile(daily_returns, 5)
# 可視化
plt.figure(figsize=(10, 6))
plt.hist(daily_returns, bins=50, alpha=0.7)
plt.axvline(x=VaR_95, color='r', linestyle='--', label=f'VaR 信頼区間 95%: {VaR_95:.4f}')
plt.title('ポートフォリオの収益のリスク値 (VaR)')
plt.xlabel('日次リターン')
plt.ylabel('頻度')
plt.legend()
plt.show()
c. 最適化型(Optimization)
最適化分析は、コスト削減、効率の向上、収益の最大化などといった特定の目標を達成するために、リソースを最適に割り当てる方法を見つけることを目的としています。
利用例:
輸送ルートの最適化、生産計画、リソース最適化などで利用されます。
分析手法:
最適化分析では、線形計画法、整数計画法、遺伝的アルゴリズムなどの最適化アルゴリズムが用いられます。
線形の目的関数を線形の制約条件の下で最大化または最小化する問題を解くのに適している「線形計画法」の場合の数理モデルの例を以下に示します。
\begin{align}
\text{minimize }\quad &c^T x \\
\text{subject to }\quad &Ax \leq b \\
&x \geq 0
\end{align}
$c$:コストベクトル
$x$:決定変数
$A$:制約行列
$b$:制約ベクトル
$minimize$ は目的関数の "最小化" を表しており、"最大化" の場合は、$maximize$ を使用します。また $subject to$ には制約条件(および変数の範囲)を記述します。
Python 実装
最適化型の分析シナリオである線形計画問題を Python で解き、その結果を可視化する例を示します。この例では、シンプルな線形計画問題を定義し、SciPy の最適化ツールを使用して解きます。そして、解の可視化を行います。
以下のコードは、線形計画問題を解くもので、2つの変数 $x_1$, $x_2$ に対する制約条件の下で、目的関数を最小化します。以下の数式で表されます。
\begin{align}
\text{minimize }\quad &-x_1 - x_2 \\
\text{subject to }\quad &2x_1 + x_2 \leq 20 \\
&x_1 + 2x_2 \leq 20 \\
&x_1 - x_2 \leq 5 \\
&x_1 \geq 0 \\
&x_2 \geq 0 \\
\end{align}
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import linprog
# 目的関数の係数(最小化したい)
c = [-1, -1]
# 不等式制約(Ax <= b)
A = [[2, 1], [1, 2], [1, -1]]
b = [20, 20, 5]
# 変数の範囲(0以上)
x0_bounds = (0, None)
x1_bounds = (0, None)
# 線形計画問題を解く
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='highs')
# 結果の表示
print("最適値:", res.fun)
print("最適解:", res.x)
# 可視化
x = np.linspace(0, 20, 400)
y = np.linspace(0, 20, 400)
X, Y = np.meshgrid(x, y)
Z = c[0]*X + c[1]*Y
plt.figure(figsize=(8, 6))
plt.contourf(X, Y, Z, levels=50, cmap='viridis')
plt.plot(x, (20 - 2*x), label=r'$2x_1 + x_2 \leq 20$')
plt.plot(x, (20 - x)/2, label=r'$x_1 + 2x_2 \leq 20$')
plt.plot(x, 5 + x, label=r'$x_1 - x_2 \leq 5$')
plt.xlim((0, 20))
plt.ylim((0, 20))
plt.plot(res.x[0], res.x[1], 'ro') # 最適解
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.legend()
plt.title('線形プログラムの最適化')
plt.show()

d. リスクヘッジ型(Risk Hedging)
リスクヘッジ分析は、潜在的な損失を軽減するためにリスクを管理し、ヘッジする戦略を開発することを目的としています。
利用例:
主にポートフォリオのリスク管理やヘッジ戦略の策定で使用され、金融市場での投資戦略や保険、契約条項に応用されたりします。
分析手法:
ポートフォリオ最適化、オプション戦略、バリューアットリスク (VaR) 計算が利用されます。
投資リターンを最大化しつつリスクを最小化するように、資産の組み合わせを決定するプロセスである「ポートフォリオ最適化」の場合は以下のように表されます。
\begin{align}
\text{minimize }\quad &\sigma_p^2 = \sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_i \sigma_j \rho_{ij} \\
\text{subject to }\quad &\sum_{i=1}^{n} w_i = 1
\end{align}
$\sigma_p^2$:ポートフォリオの分散
$w_i$:資産の重み
$\sigma_i$:資産の標準偏差
$\rho_{ij}$ は資産間の相関係数
Python 実装
リスクヘッジ型の分析シナリオであるポートフォリオ最適化を Python で実装し、その結果を可視化する例を示します。この例では、いくつかの架空の株式のリターンをシミュレートし、それらの株式を組み合わせてポートフォリオのリスク(分散)と期待リターンを最適化します。
ポートフォリオ最適化とは、投資ポートフォリオのリスクとリターンのバランスを最適化するプロセスです。
- リスク: 投資の不確実性や損失の可能性を指す。通常は「ボラティリティ」(価格の変動幅)を用いて測定される。
- リターン: 投資から得られる利益を意味する。投資家は通常、高いリターンを目指すが、それは同時に高いリスクを伴うこともある。
ポートフォリオ最適化の目的は、リスクを最小限に抑えつつ、望ましいリターンを達成する資産の組み合わせを見つけることです。これは、異なる資産間の相関関係を考慮し、リスクを分散させることで達成されます。リスクの高い資産(高ボラティリティ)とリスクの低い資産(低ボラティリティ)を組み合わせることで、全体のポートフォリオリスクを管理しつつ、リターンを最大化します。
このプロセスにおいて重要な指標の一つとして「シャープレシオ」があります。シャープレシオは、リスク調整後のリターンを測定する指標で、投資のリターンをそのボラティリティ(リスク)で割ったものです。高いシャープレシオは、単位リスクあたりの高いリターンを意味し、投資家は通常、シャープレシオが高いポートフォリオを好む傾向があります。
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as sco
# 架空の株式のリターンと分散をシミュレート
np.random.seed(42)
num_assets = 4
num_portfolios = 10000
returns = np.random.normal(0.1, 0.2, (num_assets, num_portfolios))
# ポートフォリオの期待リターン、分散、シャープ比の計算
def portfolio_performance(weights, returns):
portfolio_return = np.sum(weights * returns.mean(axis=1))
portfolio_std = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns), weights)))
return portfolio_return, portfolio_std
# 最適化関数
def minimize_risk(weights, returns):
return portfolio_performance(weights, returns)[1]
# 制約条件
constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bounds = tuple((0, 1) for asset in range(num_assets))
initial_weights = num_assets * [1. / num_assets,]
# 最適化の実行
optimal_portfolio = sco.minimize(minimize_risk, initial_weights, args=(returns,), method='SLSQP', bounds=bounds, constraints=constraints)
# 最適化されたポートフォリオのパフォーマンス
opt_return, opt_risk = portfolio_performance(optimal_portfolio['x'], returns)
# 可視化
plt.figure(figsize=(10, 6))
plt.scatter(returns.std(axis=1), returns.mean(axis=1), c=returns.mean(axis=1)/returns.std(axis=1), marker='o') # ランダムポートフォリオ
plt.scatter(opt_risk, opt_return, color='red', marker='*', s=100) # 最適化されたポートフォリオ
plt.title('ポートフォリオ最適化')
plt.xlabel('ボラティリティ')
plt.ylabel('リターン')
plt.colorbar(label='シャープレシオ')
plt.show()
4. ターゲティング型(Targeting)
ターゲティング分析は、特定の顧客セグメントや市場を特定し、ターゲットに合わせた製品やサービスを提供することを目的としています。
利用例:
マーケティング、広告、製品開発で一般的に使用され、マーケティングキャンペーン、ターゲット顧客の特定等に活用することができます。
分析手法:
ターゲティング型の分析手法は、特定の顧客グループや市場セグメントに焦点を当て、より効果的なマーケティング戦略を策定するために使用される一連の手法で、通常以下のような流れで行われます。
- 市場を小さなセグメントに分割(顧客セグメンテーション)
- クラスタリング(k 平均法など)
- マーケティング戦略の策定
- レコメンデーションエンジンを活用した顧客体験のパーソナライズ等
- 異なるマーケティングアプローチの効果を評価し、最も効果的な戦略を選択
- A/B テスト
クラスタリングのための一般的なアルゴリズムである「k 平均法」の場合、各クラスタの中心までの絶対距離を算出し、最小となるものを選択します。
\begin{align}
\text{minimize }\quad &\sum_{i=1}^{k} \sum_{x \in S_i} ||x - \mu_i||^2
\end{align}
$S_i$:クラスタ
$\mu_i$:クラスタの中心
Python 実装
ここでは、架空のデータセットを使用して、データを k 平均法でクラスタに分割し、ターゲットグループを識別する例を示します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# 架空のデータセット生成
np.random.seed(0)
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# k平均法によるクラスタリング
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
# 可視化
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5)
plt.title('K-Means クラスタリング')
plt.xlabel('特徴量 1')
plt.ylabel('特徴量 2')
plt.show()
5. 与信管理型(Credit Management)
与信管理分析は、顧客の信用リスクを評価し、信用限度やローンの承認を決定することを目的としています。
利用例:
金融機関がローン承認やクレジットスコアの計算を行う際に、信用評価、ローン審査、信用リスク評価などに利用することができます。
分析手法:
このモデルでは、ロジスティック回帰、ランダムフォレストといった様々な手法が使用されます。
与信スコアリングなどでもよく用いられるロジスティック回帰については、上述の「a. 不正検出型(Fraud Detection)」の分析手法で説明した通りです。
Python 実装
この例では、架空のデータセットを使用して、特定の特徴に基づいてロジスティック回帰による分析を行い、ローンのデフォルトの可能性といったクレジットリスクを予測します。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
# 架空のデータセット生成
np.random.seed(0)
X = np.random.randn(200, 2)
y = np.random.randint(0, 2, 200) # 0はリスクなし、1はリスクあり
# データセットをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# ロジスティック回帰モデルのトレーニング
model = LogisticRegression()
model.fit(X_train, y_train)
# テストデータに対する予測
y_pred = model.predict(X_test)
# モデルの評価
print(classification_report(y_test, y_pred))
print("混同行列:\n", confusion_matrix(y_test, y_pred))
# 可視化
plt.figure(figsize=(10, 6))
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_pred, cmap='coolwarm', edgecolor='k', s=40)
plt.title('ロジスティック回帰を用いた信用リスク予測')
plt.xlabel('特徴量 1')
plt.ylabel('特徴量 2')
plt.show()
6. 評価・要因分析(Evaluation & Factor Analysis)
評価・要因分析は、データ内の主要な要因や変数を特定し、それらが全体の結果にどのように影響するかを理解することを目的としています。
利用例:
市場調査、製品開発、顧客満足度の分析などで、製品評価、顧客満足度分析、要因の影響評価を行う際に使用されたりします。
分析手法:
評価・要因分析シナリオでは、因子分析、回帰分析、クロス集計など様々な分析手法が存在しており、これらを用途や状況に応じて使い分けます。分析手法を用途別に分類すると以下のようになります。
-
要因分析の用途
- 主成分分析(PCA)
- 因子分析
-
評価分析の用途
- 回帰分析
- データ探索的分析
-
両用途で使用可能
- クロス集計
Python 実装
要因分析で用いられる主成分分析(PCA)を使用して3次元データを2次元に削減した後の可視化です。左側のグラフは元の3次元データを示しており、右側のグラフはPCAを適用した後の2次元データを示しています。このプロセスにより、データの主要な特徴を保持しながら次元を削減することができます。
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
# ランダムな3次元データを生成
np.random.seed(0)
X = np.random.rand(100, 3)
# PCAを適用して3次元から2次元へ次元削減
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# 元の3次元データの可視化
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(121, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2])
ax.set_title("元の3次元データ")
ax.set_xlabel("X軸")
ax.set_ylabel("Y軸")
ax.set_zlabel("Z軸")
# PCA適用後の2次元データの可視化
ax2 = fig.add_subplot(122)
fig.subplots_adjust(wspace=0.3)
ax2.scatter(X_pca[:, 0], X_pca[:, 1])
ax2.set_title("PCA 後の2次元データ")
ax2.set_xlabel("主成分1")
ax2.set_ylabel("主成分2")
plt.rcParams["font.size"] = 6
plt.show()
7. コンテクスト・アウェアネス型(Context Awareness)
コンテクスト・アウェアネス分析は、ユーザーの状況や環境を理解し、その情報を基に適切な応答やサービスを提供することを目的としています。
利用例:
スマートデバイス、パーソナライズされたサービス、状況に応じた広告などに使用されます。
分析手法:
センサーデータ解析、位置情報データ、リアルタイムデータ処理を基に、条件付き確率モデル、時系列分析、クラスタリング、決定木モデル、ベイジアンネットワークなどが用いられます。
- 条件付き確率モデル: 特定の条件下での事象の発生確率をモデル化する手法
- 時系列分析: 時間に依存するデータの特性を分析する手法
- クラスタリング: 類似の特性を持つデータポイントをグループ化する手法
- 決定木モデル: データを分類または回帰するための木構造ベースのモデル
- ニューラルネットワークと深層学習: 大量のデータから複雑なパターンを学習するための強力なモデル
- 関連ルールマイニング: データ内のアイテム間の関連ルールを見つけ出す手法
- ベイジアンネットワーク: 変数間の確率的関係をモデル化する手法
Python 実装
今回は、条件付き確率モデルを Python で実装し、その結果を可視化します。この例では、温度と湿度を基にエアコンがオンになる確率をモデル化しています。
カラーマップはエアコンがオンになる確率の分布を表し、散布図の点は実際のデータポイント(赤はエアコンがオン、青はオフ)を示しています。これにより、特定の温度と湿度の条件下でエアコンがオンになる確率を視覚的に理解することができます。
ソースコードで実装された条件付き確率モデルは、ガウシアンナイーブベイズ分類器を使用しています。これは、特徴間の独立性を仮定し、ガウス分布を用いてクラスの条件付き確率をモデル化するものです。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.naive_bayes import GaussianNB
# サンプルデータの生成(温度、湿度、エアコンの状態)
np.random.seed(0)
temperature = np.random.normal(25, 5, 100) # 平均25度、標準偏差5の温度
humidity = np.random.normal(50, 10, 100) # 平均50%、標準偏差10%の湿度
aircon_status = np.random.choice([0, 1], 100) # エアコンの状態(0: OFF、1: ON)
# データセットの準備
# X は特徴(温度と湿度)、y は目標変数(エアコンの状態)
X = np.column_stack((temperature, humidity))
y = aircon_status
# 条件付き確率モデル(ガウシアンナイーブベイズ)の作成と学習
model = GaussianNB()
model.fit(X, y)
# 可視化のためのグリッド作成
xx, yy = np.meshgrid(np.linspace(15, 35, 100), np.linspace(30, 70, 100))
grid = np.c_[xx.ravel(), yy.ravel()]
# 与えられたグリッド上の各点についてエアコンがオン(1)である確率を計算
probs = model.predict_proba(grid)[:, 1].reshape(xx.shape)
# 可視化
plt.figure(figsize=(10, 6))
contour = plt.contourf(xx, yy, probs, cmap="RdYlBu", alpha=0.8)
plt.colorbar(contour)
# 散布図
scatter = plt.scatter(temperature, humidity, c=aircon_status, cmap="RdYlBu", marker='x')
# 凡例の修正
legend1 = plt.legend(*scatter.legend_elements(), title="エアコンの状態")
legend1.get_texts()[0].set_text('OFF')
legend1.get_texts()[1].set_text('ON')
plt.gca().add_artist(legend1)
# ラベルとタイトル
plt.xlabel("温度 (°C)")
plt.ylabel("湿度 (%)")
plt.title("エアコンがONになる確率")
plt.rcParams["font.size"] = 8
plt.show()
8. プロセス・トレース型(Process Trace)
プロセス・トレース分析は、ビジネスプロセスやシステムの動作を追跡し、効率性や問題点を特定することを目的としています。
利用例:
プロセス最適化、製造プロセス管理、品質管理。業務改善、システム最適化などに使用されます。
分析手法:
-
データ収集と初期分析:
- 最初に、対象となるプロセスからデータを収集します。このデータには、トランザクションログ、イベントログ、センサーデータなどが含まれる場合があります。
- データ分析のフェーズでは、この収集されたデータを初期的に解析して、データの品質を評価し、基本的な傾向やパターンを特定します。
-
プロセスマイニング:
- プロセスマイニングは、収集されたデータを用いて実際のプロセスフローを発見し、可視化する技術です。これにより、プロセスの動作を理解し、ボトルネックや非効率な部分を特定できます。
- プロセスマイニングは、データから直接プロセスモデルを生成することができ、プロセスの実際の動作を反映した客観的なビューを提供します。
-
プロセスモデリング:
- プロセスマイニングによって得られた情報を基に、プロセスモデリングが行われます。このステップでは、プロセスの詳細なフローと構造をモデル化し、文書化します。
- プロセスモデリングにより、プロセスの効率化や改善のための戦略を策定するための基礎が形成されます。
-
マルコフモデルの適用:
- マルコフモデルは、プロセス内の各イベントや状態間の遷移確率をモデル化します。これにより、将来のプロセスの状態や挙動を予測することができます。
- プロセスの各段階での確率的な振る舞いを分析することにより、より効果的な意思決定やリスク管理が可能になります。
この処理フローにより、組織はプロセスの現状を深く理解し、効率化や最適化の機会を特定することができます。プロセスマイニングとデータ分析によって得られた洞察をプロセスモデリングで具体化し、マルコフモデルを使用して将来のプロセスの挙動を予測することで、組織はよりデータ駆動型の意思決定を行うことができるようになります。
Python 実装
プロセス・トレース型の分析シナリオであるマルコフモデルを Python で実装し、その結果を可視化する例を示します。この例では、簡単なマルコフチェーンを作成し、状態遷移をシミュレートして可視化します。
以下のコードは、マルコフチェーンの状態遷移行列を定義し、ある状態から始めて複数ステップを通じての遷移をシミュレートするものです。
import numpy as np
import matplotlib.pyplot as plt
# 状態遷移行列の定義
# 例: 3つの状態があるマルコフチェーン
transition_matrix = np.array([[0.9, 0.075, 0.025],
[0.15, 0.8, 0.05],
[0.25, 0.25, 0.5]])
# 初期状態の定義(状態1からスタート)
current_state = np.array([1, 0, 0])
states_over_time = [current_state]
# マルコフチェーンのシミュレーション(例: 50ステップ)
num_steps = 50
for _ in range(num_steps):
current_state = current_state.dot(transition_matrix)
states_over_time.append(current_state)
# 結果の可視化
states_over_time = np.array(states_over_time)
plt.figure(figsize=(10, 6))
plt.plot(states_over_time)
plt.title('マルコフ連鎖における時間経過に伴う状態確率')
plt.xlabel('時間ステップ')
plt.ylabel('確率')
plt.legend(['状態 1', '状態 2', '状態 3'])
plt.show()
このソースコードは、3つの状態を持つマルコフチェーンのシミュレーションとその結果の可視化を行っています。
マルコフチェーン
マルコフチェーンは、確率過程の一種で、次の状態が現在の状態にのみ依存する(過去の状態には依存しない)という特性を持ちます。これは「無記憶性」とも呼ばれます。
状態遷移行列
状態遷移行列は、マルコフチェーン内の各状態から次の状態への遷移確率を表します。このケースでは、3x3 の行列が使用され、3つの状態があります。行列の各行は、ある状態から次のステップで別の状態に移る確率を表し、行の合計は1になります。
ソースコードの解説
- 状態遷移行列の定義:
- 3x3の行列で、各要素は特定の状態から次の状態への遷移確率を表しています。
- 例えば、最初の行
[0.9, 0.075, 0.025]は、状態1から次のステップで状態1に留まる確率が 0.9、状態2へ移る確率が 0.075、状態3へ移る確率が 0.025 であることを意味します。
- 初期状態の定義:
-
[1, 0, 0]は、最初に状態1にいることを表しています。
-
- マルコフチェーンのシミュレーション:
- 50ステップを通じてマルコフチェーンをシミュレートします。各ステップで、現在の状態ベクトルを状態遷移行列に掛けて、次の状態の確率分布を計算します。
- 結果の可視化:
- 生成された状態確率の時系列データをプロットします。
-
plt.plot(states_over_time)は、時間経過に伴う各状態の確率を描画します。 - 例えば、線グラフの各線は、特定の状態(状態1、状態2、状態3)にいる確率が時間とともにどのように変化するかを示しています。











