はじめに
研究開発補助をお願いしている現在,博士課程在学中の高田珠武己さんに,Andrew Ng 先生の Coursera "Machine Learning" https://www.coursera.org/learn/machine-learning を受講してもらったところ,序盤の線形回帰モデルの説明でよくわからないところ(データ規格化の理論的背景)がでてきてしまい,議論しているうちに思わぬ深み(甘利先生が発見された自然勾配法)まで話が進んでしまいました,というお話.
結論を先取りすると,回帰タスクにおける特徴量の前処理は,自然勾配法による最適化の過程を,ヒューリスティックに近似したものとみなせる(=最適化手法として,自然勾配法を選べば,特徴量の前処理は不要),ということになります.それでは,議論を追ってみましょう.
問題設定(線形回帰モデル)
Ng 先生が講義の題材とした問題は次のとおり:
移動式屋台をある都市に新規出店した場合に期待される収益を,各都市の人口等を説明変数(特徴量)として線形回帰モデルを使って予測する.
実際に,講義で提供されているデータをプロットすると,横軸(各都市の人口),縦軸(各都市における移動式屋台の収益)としたときの変数間の関係は次のようになっている.
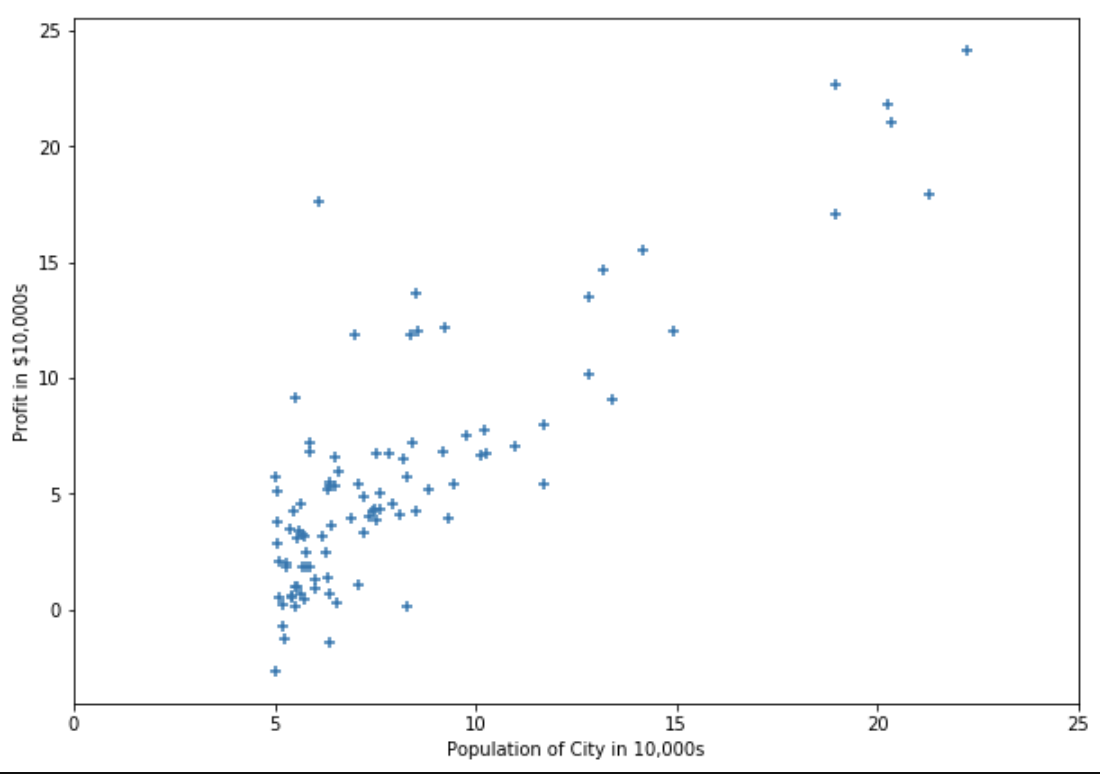
この散布図をみると,特徴量が,各都市の人口のみの,1変数線形回帰モデルでは心もとないことがわかる.そこで,ここからは,既に出店した都市の数(訓練データの数)を $m$,特徴量の数を $n$ として,多変数版の線形回帰モデルを考えることにする.
特徴量を $x_j^{(i)}$ ,パラメータを $\theta = (\theta_0 ,\theta_1 ,\dots ,\theta_n)^\mathrm{T}$ とすると,収益の仮説は $h_\theta (x_1^{(i)} ,\dots ,x_n^{(i)})=\theta_0 + \theta_1 x_1^{(i)} +\dots + \theta_n x_n^{(i)}$ と表される.ここで,0番目の特徴量として $x_0^{(i)} =1$ を導入し,$x^{(i)} =(x_0^{(i)} ,x_1^{(i)} ,\dots ,x_n^{(i)})^\mathrm{T}$ を特徴量ベクトルとすると,仮説は $h_\theta (x^{(i)})=(x^{(i)})^\mathrm{T} \theta$ のように内積の形で書ける.
特徴量ベクトル $x^{(i)}$ の転置をすべてのデータについて縦に並べた行列を
\begin{gather*}
X=
\begin{pmatrix}
(x^{(1)})^\mathrm{T} \\
\vdots \\
(x^{(m)})^\mathrm{T}
\end{pmatrix}
\end{gather*}
とする.定義から $X$ は $m\times (n+1)$ 行列であり,1列目の要素はすべて1である.
仮説$h_\theta (x^{(i)})$をすべてのデータについて縦に並べたベクトルは$X\theta$のように簡単に表せる.この仮説$X\theta$が収益(ターゲット)$y=(y^{(1)} ,\dots ,y^{(m)})^\mathrm{T}$と近くなるようなパラメータ$\theta$を見つけたい.
コスト関数の導入
コスト関数 $J(\theta )$ は,ターゲットに対する仮説の平均2乗誤差である:
\begin{align}
J(\theta )=\frac{1}{2m} \sum _{i=1}^m (h_\theta (x^{(i)})-y^{(i)})^2 =\frac{1}{2m} (X\theta -y)^2 .
\end{align}
コスト $J(\theta )$ が最小となるような最適パラメータ $\theta$ を見つけることで,仮説とターゲットがなるべく近くなるようにすることができる.
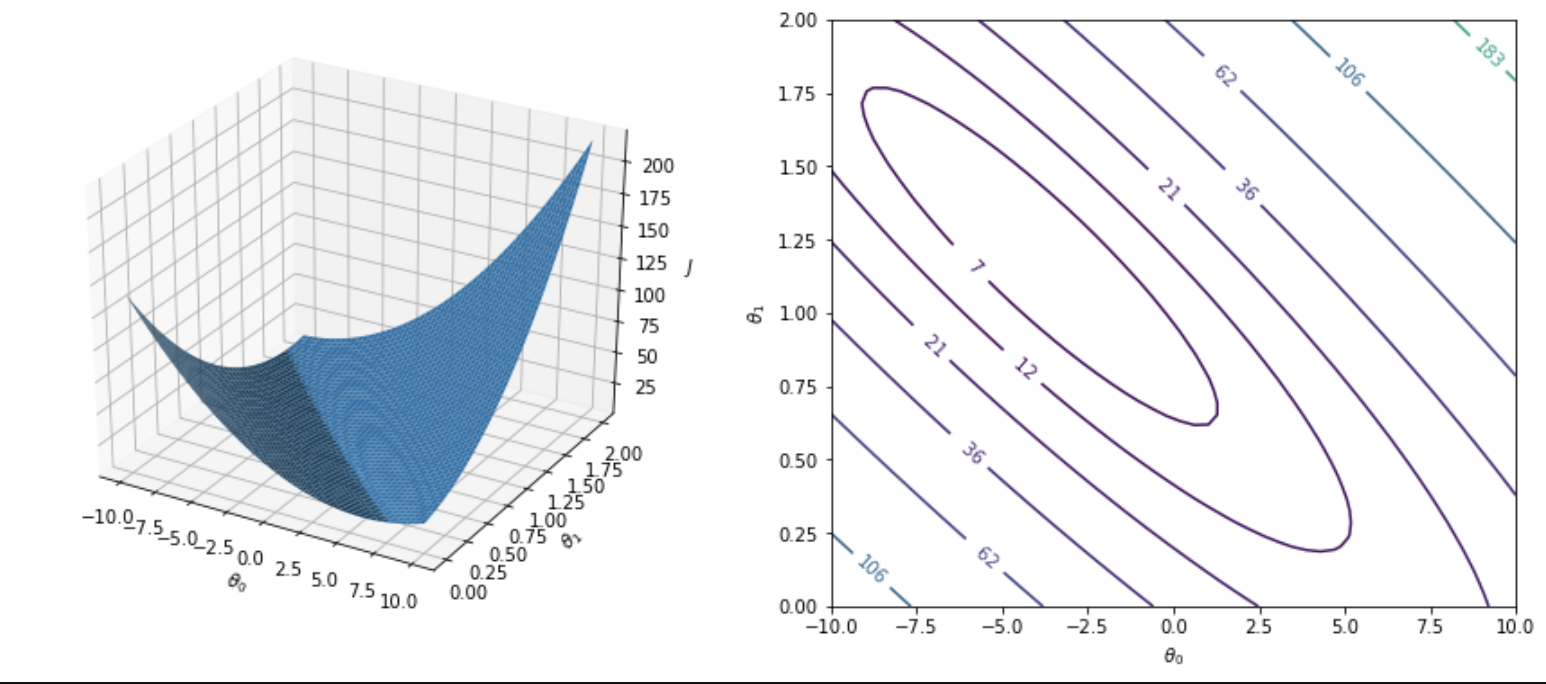
各都市の人口を特徴量とした1変数線形回帰モデルの場合は,コスト関数は次のような曲面を描く.
勾配法
勾配法とは,コスト $J(\theta )$の勾配ベクトル$\partial J/\partial\theta$ と反対方向にパラメータ $\theta$ を動かすことで,コストが最小となるパラメータを見つける方法である.コストが最小となるとき勾配が消失する:$\partial J/\partial\theta =0$. パラメータ $\theta$ の更新式は次のように表される:
\begin{align}
\theta\leftarrow\theta -\eta\frac{\partial J(\theta )}{\partial\theta} = \theta -\frac{\eta}{m} X^\mathrm{T} (X\theta -y)=\theta -\frac{\eta}{m} X^\mathrm{T} X (\theta - \theta^{\ast}).
\end{align}
ここで,$\eta$ は学習率,$\theta^{\ast}$ はパラメータの最適解である.学習率が小さすぎると最適パラメータにたどり着くのに時間がかかりすぎてしまう.逆に,学習率が大きすぎると更新に伴ってコストが下がらなかったり発散したりしてしまう.適切に学習率を選べていればコストは更新とともに下がっていく.
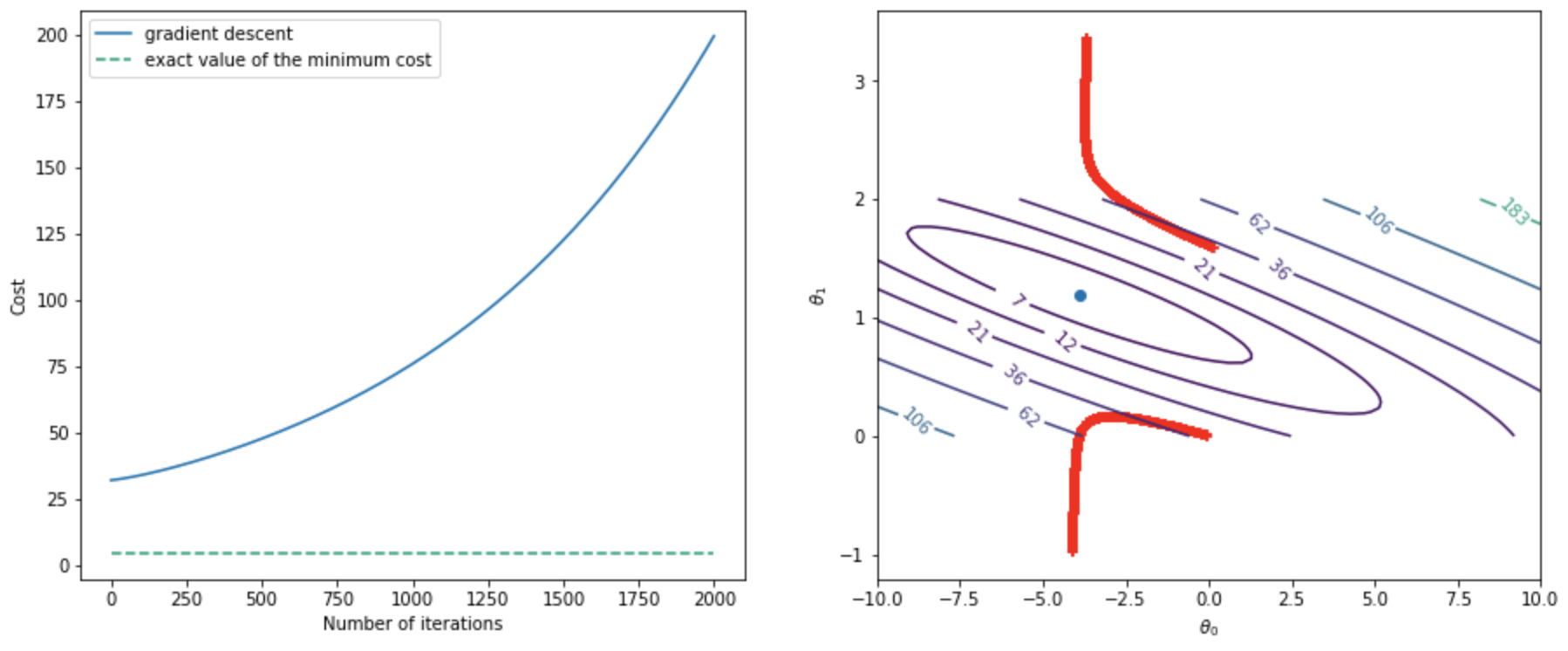
実際に,勾配法をつかってパラメータを更新していくと,コスト関数は減少していくことがわかる(1変数線形回帰モデルの場合をプロット).ただし,パラメータの初期値は原点とした.
- 学習率が適切なレンジに収まるとき,パラメータは最適解に向かって収束する

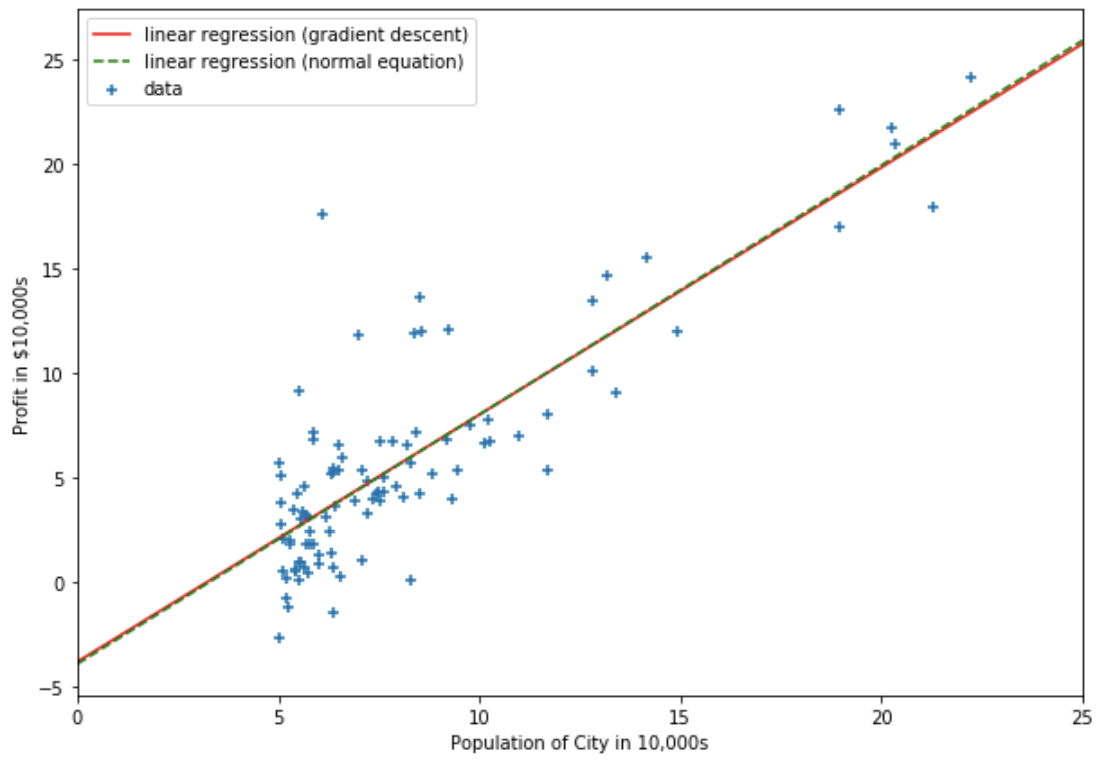
勾配法によって求められたパラメータを線形回帰モデルに代入すると,回帰直線は次のようになる.
- 一方,学習率が適切なレンジに収まらないと,パラメータは発散する

特徴量の前処理(規格化,白色化)
上記のように,学習の過程でパラメータが発散してしまう場合,特徴量に前処理を施すことで学習が上手く進むようになることがある.特徴量が $x_j$ ($j=1,\dots ,n$) のように複数ある場合,それぞれが異なるスケールを持っていることが一般的であり,これによってパラメータ空間上の勾配のスケールも成分ごとに不均一になってしまうと勾配法が機能しなくなる.そこで,すべての特徴量が大体同じスケールに収まるように規格化することで勾配法の効率を改善させる.訓練データのラベルを$(i)$ ($i=1,\dots ,m$) と書くと,
\begin{align}
x_j^{(i)} \leftarrow\frac{x_j^{(i)} -\mu _j}{\sigma _j}
\end{align}
を新たな特徴量として用いることで規格化できる.ただし,$\mu _j$, $\sigma _j$は$j$番目の特徴量の平均値,標準偏差である:
\begin{align}
\mu _j =\frac{1}{m} \sum _{i=1}^m x_j^{(i)} ,\quad\sigma _j =\sqrt{\frac{1}{m} \sum _{i=1}^m (x_j^{(i)} -\mu _j)^2} .
\end{align}
さらに白色化は,特徴量間の無相関化を要請する.
\begin{align}
X^\mathrm{T}X = I.
\end{align}
このとき,勾配法によるパラメータの更新式は次のように書き直せる(パラメータ空間(統計多様体)上の e-測地線をあらわす式になっている).
\begin{align}
\theta \leftarrow \theta -\frac{\eta}{m} (\theta - \theta^{\ast}) = \left( 1-\frac{\eta}{m} \right)\theta + \frac{\eta}{m}\theta^{\ast}.
\end{align}
- 特徴量に規格化,白色化を施すと,大きな学習率でもパラメータが収束するようになるほか,勾配法が描くパラメータ更新の軌跡が,次節で紹介する自然勾配法の軌跡に近づく(白色化の場合は,更新幅(学習率)をのぞいて軌跡が完全に一致する).図は,特徴量に規格化を施した場合:

自然勾配法
甘利先生によって発見された自然勾配法は,勾配法の更新式に,Fisher 計量の逆行列 $g^{-1}(\theta)$ を加えることを要請する.
\begin{align}
\theta \leftarrow \theta -\eta g^{-1}(\theta ) \frac{\partial J(\theta )}{\partial\theta} = \theta -\frac{\eta}{m} g^{-1}(\theta ) X^\mathrm{T} (X\theta -y) = \theta -\frac{\eta}{m} g^{-1}(\theta ) X^\mathrm{T} X(\theta - \theta^{\ast}).
\end{align}
ここで,Fisher 計量 $g(\theta)$ を導入する.線形回帰モデルに正規分布に従うノイズ項を追加して,特徴量 $x$ とターゲット $y$ が結合分布
\begin{align}
p(x,y\vert\theta )=p(x)p(y\vert x,\theta )=\frac{1}{\sqrt{2\pi\sigma ^2}} p(x)\exp\left( -\frac{1}{2\sigma ^2} (y-h_\theta (x))^2 \right)
\end{align}
に従うとする.ただし,分散 $\sigma^{2}$ は定数として,推定の対象外とする(あるいは $\sigma\to 0$ の極限をとって決定論的な予測を考える).このとき,微小に離れた2つの分布$p(x,y\vert\theta )$, $p(x,y\vert\theta +d\theta )$ の間の擬距離として Kullback-Leipler (KL) ダイバージェンスを考えると
\begin{align}
D[p(x,y\vert\theta )\Vert p(x,y\vert\theta +d\theta )]=\int d^{n+1} x\, dy\, p(x,y\vert\theta )\log\frac{p(x,y\vert\theta )}{p(x,y\vert\theta +d\theta )} .
\end{align}
KLダイバージェンスを $d\theta$ の2次まで展開すると,次式が得られる(ここでも Einstein の縮約規則を用いる):
\begin{align}
D[p(x,y\vert\theta )\Vert p(x,y\vert\theta +d\theta )]=\frac{1}{2} g_{ij} (\theta )\, d\theta ^i d\theta ^j +\mathcal{O} (\lvert d\theta\rvert ^3).
\end{align}
ただし,$g_{ij} (\theta)$ は Fisher 情報行列の成分と呼ばれ,次のように定義される:
\begin{align}
g_{ij} (\theta )=\mathrm{E}_{p(x,y\vert\theta )} [\partial _i \log p(x,y\vert\theta )\,\partial _j \log p(x,y\vert\theta )].
\end{align}
Fisher 情報行列 $g(\theta)=(g_{ij}(\theta))$ は計量として用いることができる.すなわち,Fisher 計量は統計多様体上の微小に離れた2点間の距離を定める.いま考えているモデル(線形回帰モデル)では $h_\theta (x)=\theta ^i x_i$ なので,Fisher 計量の成分は
\begin{align}
g_{ij} (\theta )=\frac{1}{\sigma ^2} \mathrm{E}_{p(x,y\vert\theta )} [x_i x_j]=\frac{1}{\sigma ^2} \mathrm{E}_{p(x)} [x_i x_j].
\end{align}
となる.Fisher 計量は特徴量の事前分布 $𝑝(𝑥)$ に関する平均で与えられているが,分布 $𝑝(𝑥)$ はわからないので,データに関する平均値で近似することにして
\begin{align}
g(\theta )=\frac{1}{\sigma ^2 m} \sum _{d=1}^m x_i^{(d)} x_j^{(d)} = \frac{1}{\sigma ^2 m} X^\mathrm{T} X.
\end{align}
を得る.ここから,線形回帰モデルでは,パラメータの更新式を次のような簡単なかたちに書き直せることがわかる( $g^{-1}(\theta) X^\mathrm{T} X = \sigma ^2 m I$, $\eta\sigma^{2}=\eta^{\prime}$ ).
\begin{align}
\theta\leftarrow \theta - \eta^{\prime} (\theta - \theta^{\ast}) = \left( 1-\eta^{\prime} \right)\theta + \eta^{\prime}\theta^{\ast}.
\end{align}
この新しい更新式は,式のなかに $X^\mathrm{T} X$ を含まないため,特徴量に対する前処理(規格化や白色化など)の影響を受けない(=最適化手法として,自然勾配法を選べば,特徴量の前処理は不要).また,パラメータの更新が,初期値から最適解に向かって一直線に進むパラメータ空間(統計多様体)上の測地線に乗っていることもわかる.

ここまでの説明をみると,自然勾配法は万能であるかのように感じられたかもしれない.が,実際には線形回帰モデルでは自然勾配法を使うメリットは少ないと言えよう.というのも,線形回帰モデルの場合は,自然勾配法を実行する代わりに,最適解を正規方程式から求めてしまえばよいからである.また,正規方程式の解を求められない状況,すなわち特徴量の数 $n$ が多すぎて $X^\mathrm{T} X$ の逆行列を求められない状況では,自然勾配法も実行することができない.このような状況では通常の勾配法の方が効率がよい(ただし特徴量の規格化は前処理として行っておく必要がある).
したがって,自然勾配法が威力を発揮するのはむしろ非線形回帰モデル(ニューラルネットなど)を使用する場合であると考えられる.Fisher 計量はパラメータの数の次元を持つので,パラメータが多すぎなければ逆行列を計算することができ,勾配法よりも効率よく最適解を求めることが可能になる.もちろん線形回帰以外では正規方程式のように最適解を求めることができないので,自然勾配法の利用は有効である.また,ニューラルネットで自然勾配法を用いると特徴量の規格化が必要なくなると考えられる.なぜなら,規格化されている特徴量から規格化されていない特徴量への変換は1層目のパラメータの線形変換に対応し,1層目の自然勾配はパラメータと同じ変換則を満たすので,特徴量を規格化しなくても自然勾配法の性能は変わらないからである.
問題設定の一般化(非線形回帰モデル,ロジスティック回帰,ニューラルネット(MLP)回帰等)
議論が長くなってしまったので,前編・後編の2本立てにします.
次回予告としては,自然勾配法を使えば,特徴量の前処理が不要になるところは,非線形回帰モデルでも不変ということを言おうとしています(現在,確認中).ヒューリスティックなデータ前処理よ,さらば.
