はじめに
最近ずっとリザバーコンピューティングの物理リザバーを作りたいと思っています.
今回の記事では,物理リザバーが満たす条件をまとめて,どんな物理リザバーを作成するか作戦を立てたいと思います.
しかし,私はリザバーコンピューティングは愚か,機械学習の専門家でも無いため,詳しい内容は挙げさせていただいた参考文献をご参照ください.
出発点
私がリザバーコンピューティングについて興味を持ったきっかけは,学会でそれに関する発表を聞いたことです.
詳しいことは専門家の文献を参照していただきたいのですが,どうやら,ニューラルネットワークの中間層部分(出力層以外)をリザバーと呼ばれるトレイナブルではない部分に置き換えることで,計算コストを大きく削減するスキームのようです(図1).
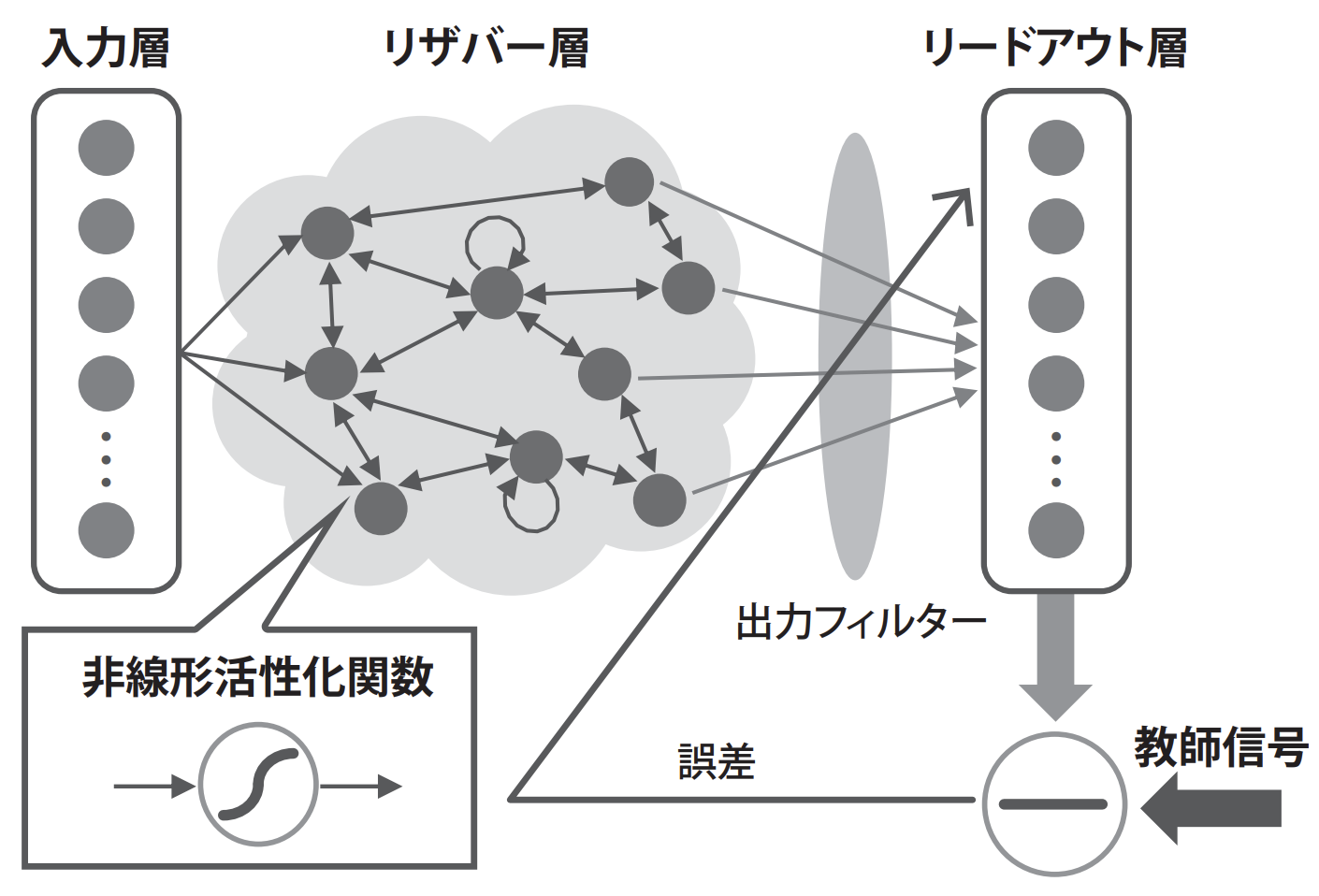
図1の出典 : 山根敏志, "図1: リザバー・コンピューティングの概念図", "物理リザバー・コンピューティングによる機械学習デバイスとエッジ・コンピューティングへの応用", ProVISION No.95 / 2019.
以下では,物理系のリザバー層が満たすべき条件をまとめて,作成に向けて物理リザバーの候補をまとめたいと思います.
物理リザバー
物理リザバーには様々な系が提案されています.たとえば,タコの足を模したシリコンのロボットアームのダイナミクスなどをがあります.
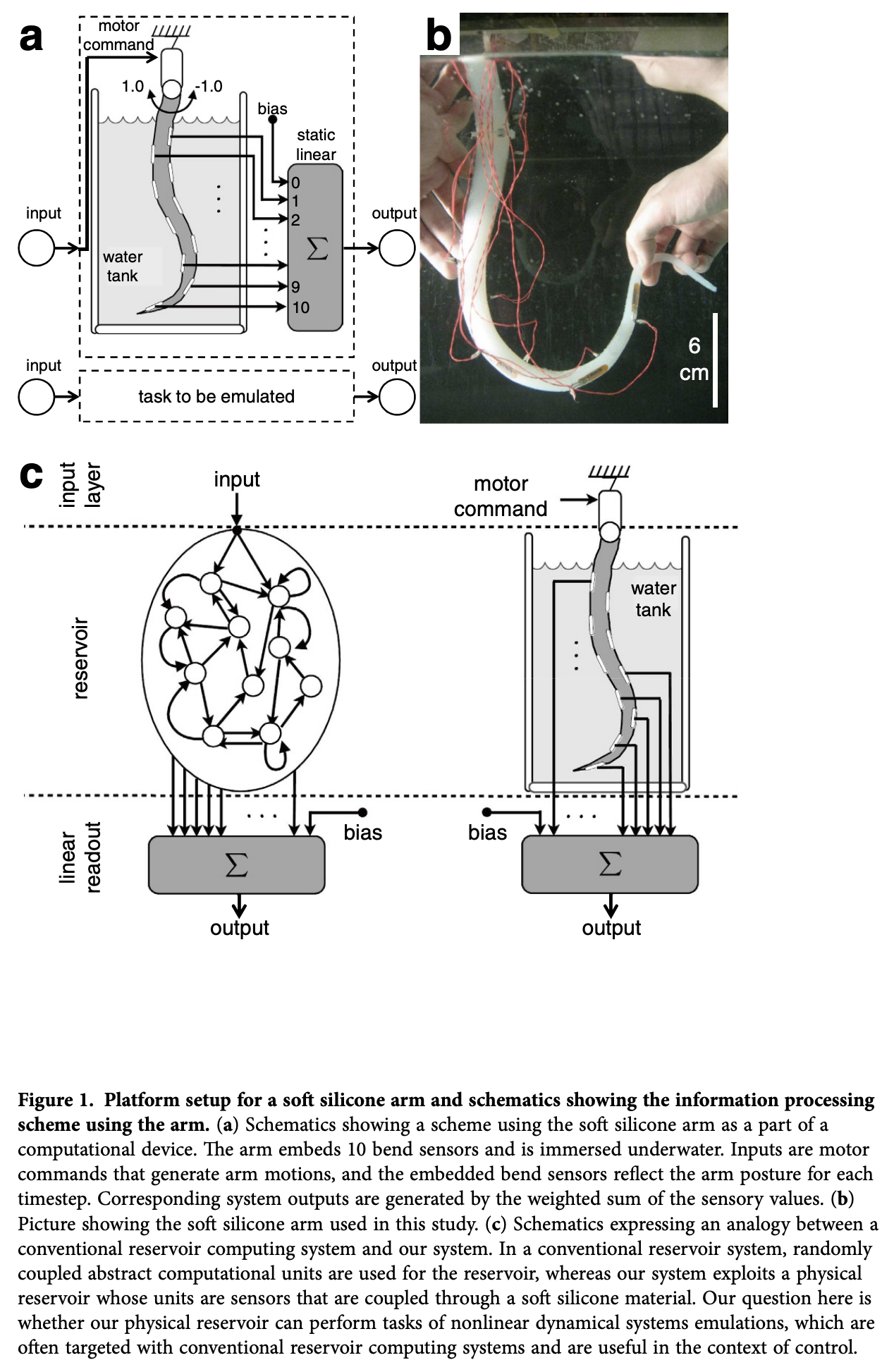
図2の出典 : Nakajima, K., Hauser, H., Li, T., & Pfeifer, R. (2015). Information processing via physical soft body. Scientific reports, 5(1), 10487, Figure. 1.
他にも,スピン系,電子回路,生物などを物理リザバーとして用いるものが提案されています.しかし,当然,どんなものでもリザバーとして使えるものになるとは限りません.
ここで,どんな系が物理リザバーに向いているのかをまとめてみます(以下,[1]).もっとも基本的で重要な性質は,共通入力信号同期と呼ばれるものです.
離散時間$k$に対して,リザバー$r(k)$は次のように定式化できます.
\boldsymbol{r}(k) = \boldsymbol{F}(k)(\boldsymbol{r}(k-1), s(k)). \tag{1}
ここで,$\boldsymbol{r}(k) \in \mathbb{R}^N$, $\boldsymbol{F}(k) : \mathbb{R}^N\times \mathbb{R} \rightarrow \mathbb{R}^N$,$s(k)$は入力信号です.リザバーは力学系$\boldsymbol{F}(k)$と書けるように,同じ入力に対しては同じ出力になる必要があります.この性質が担保されているからこそ,出力層で学習することが出来るわけです.この性質を数理的に考え直してみます.2つの異なるリザバーの初期状態,$\boldsymbol{r}(0)$,$\boldsymbol{r}'(0)$の基で共通の入力信号$s(k)$に対する出力は式(1)にしたがって時間発展します.十分に時間発展した後の状態がある1つの状態に収束する場合$|\boldsymbol{r}(k) - \boldsymbol{r}'(k)| = 0 (k \rightarrow \infty)$,この性質を共通入力信号同期と呼びます.共通入力信号同期である系であれば,原理的にその系をリザバーとして用いることが出来ます.
上で示した最低限の条件以外にも,経験的にリザバーとして適した系の性質が知られているようです.それが,"edge of chaos"と"短期記憶と非線形変換のトレードオフ関係"と呼ばれるものです.詳しくは,犬伏正信, & 吉村和之[1]を参照してください.
なにはともあれ,同じ入力に対して同じ出力が得られて,非線形性が強い系を探せばよいということになります.
今後のこと
今日,タコの足や単細胞生物をリザバーにすることが提案されています.そんなふうに自由にリザバーを探して良いならば,自分だけのリザバーを見つけたいと思うわけです.
第1章の記事では具体的にどんな物理リザバーにするかを絞りたいと思います.
ということで,本記事では最後に,物理リザバーの候補として考えたものを2つ以下に列挙します.
- 入力 : ギターの弦の組み合わせと弦を弾く強さ, 出力:音程
- 非線形光学素子: 光学系内で非線形光学素子(あるあるそうだけど,一旦の候補)
近い内に物理リザバーを構築し,ベンチマークのデータセットに対してテストの実験を行いたいです.
参考文献
[1] 犬伏正信, & 吉村和之. (2019). リザバーコンピューティングに適した力学系の特性と構造. 電子情報通信学会誌, 102(2), 114-120.