はじめに
皆さん愛媛に来たことはありますか。私は愛媛県出身で, 東京の友人によく愛媛旅行を勧めます。しかし, 来た人は1人もいません。なぜ魅力いっぱいの愛媛に誰も来てくれないのか。思い返せば, 来い来いと言ってばかりで, 明確な旅行プランの提案はしたことがありませんでした。そこで今回は, 巡って欲しい箇所をいくつかピックアップし, 入念なプランを立てることにしました。
問題設定
今回の問題設定はこんな感じになります。
「松山空港をスタート・ゴール地点とし, 観光名所 10 箇所を最短経路で回りたい」
選りすぐりの愛媛の名所 10 + 1!(私が行ったことない場所もあるのは🤫)
| 番号 | 名称 | 備考 |
|---|---|---|
| 0 | 松山空港 | 旅のスタート・ゴール地点 |
| 1 | 道後温泉 | 日本三古湯の一つで, 日本最古の温泉 |
| 2 | 松山城 | 天守閣が現存する城 |
| 3 | 宇和島城 | 天守閣が現存する城 |
| 4 | 下灘駅 | 日本一美しいと呼ばれている無人駅 |
| 5 | 市場食堂 | 2021 年に定食部門で 100 名店に選ばれた店 |
| 6 | 宇和米博物館 | 日本一⻑い廊下のある博物館 |
| 7 | 四国カルスト | 日本三代カルストの一つ |
| 8 | 石鎚山 | ⻄日本最高峰の山 |
| 9 | マイントピア別子 | 別子銅山を利用した鉱山テーマパーク |
| 10 | 内子の街並み | 江戸時代当時の面影を残した街 |
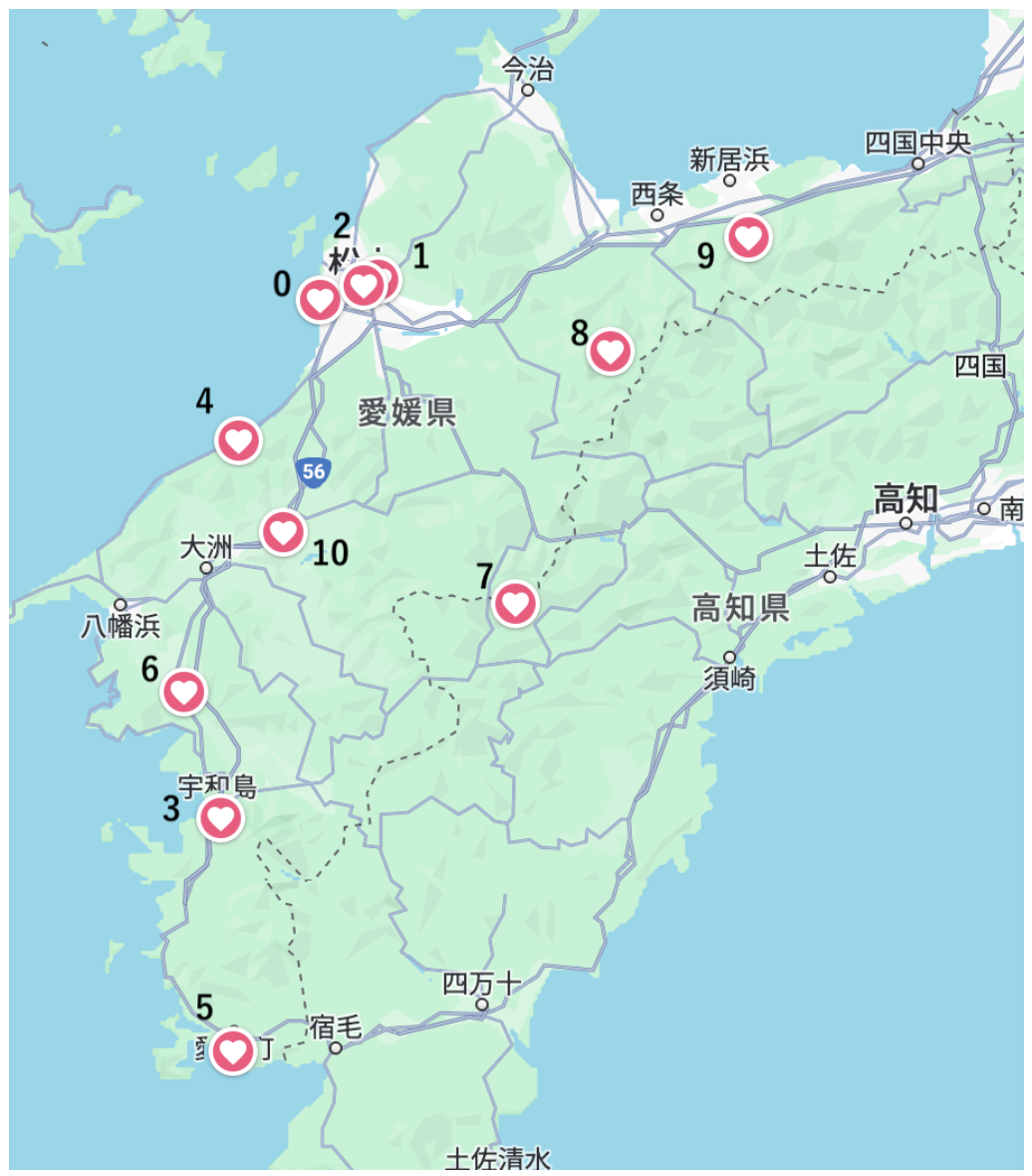
各地点の位置関係は下の図の通りです。
問題の定式化
この問題は, 「巡回セールスマン問題」(以下TSP)と呼ばれる数理的な最適化問題に帰着できます。特に今回は, 各地点同士のコストが地図上の距離に依存しているため, 三角不等式の制約付きの「メトリックTSP」と捉えることができます。細かい説明は省くので, 気になる方はぜひ調べてみてください。厳密に定式化すると, 以下のようになります。
「観光名所の集合 ${V} = \lbrace 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \rbrace$ と, 各観光名所同士のペアの集合 ${E} \subseteq {V}$, そして, ${E}$ のそれぞれの距離 $w > 0$ によって定まる完全グラフ ${K}$ とツアーの始点 $s = 0$ を入力とし, 重み最小のハミルトン閉路 ${C}^*$ を出力するメトリック TSP 問題」
解法
さあ, あとは解くだけです。メトリックTSPは, 数理最適化の世界では NP困難 な問題の一つであり, 簡単にいうと扱う数が増えると一気に解くのが難しくなります。四国88ヶ所でメトリックTSPを解くのにどれだけかかるかChatGPTに計算させると, 手元のパソコンで50億年くらいかかるそうです。なんですかこのバカみたいな数字は。
そうなんです。パソコンをもってしても, NP困難な問題は解くのが難しいのです。
ではどうするか。厳密解をもとめられなくても, それに近しい近似解であれば, どうにか求めることができます。このような, 近似解を求めるアルゴリズムをそのまま近似アルゴリズムと言います。解けないなら, せめてそれに近い値を導こうということです。
ちなみに, 今回の問題を厳密に解くためのアルゴリズムの一つに動的計画法がありますが, これに必要な時間計算量は $O(n^2 \cdot 2^n)$ です。今回は $n=11$ なので, パソコンの計算量が1秒あたり$10^8$回の計算ができるとすれば, 1秒もかからず終わってしまいます。$n$が小さいおかげで, 簡単に厳密解を求められそうです。
実装
まずは, 各地点同士のコスト(距離)を定義したコスト行列を定義します。今回は少なめだったのでちまちま手作業でやりましたが, Google Map の Distance Matrix API を使えば, 簡単にコスト行列を得ることができます。量が多い場合は活用しましょう。
costMatrix = [
# 0 1 2 3 4 5 6 7 8 9 10
[ None, 9.4, 7.0, 94, 27, 137, 77, 82.4, 85.5, 73.7, 46.9],
[ 9.4, None, 2.1, 92, 35, 135, 75, 79.2, 82.2, 71.4, 44.6],
[ 7.0, 2.1, None, 91, 29, 135, 75, 78.1, 81.1, 70.3, 43.5],
[ 94, 92, 91, None, 68, 44, 22, 79, 134, 148, 52.3],
[ 27, 35, 29, 68, None, 111, 52, 95.4, 98.5, 90.0, 31.9],
[ 137, 135, 135, 44, 111, None, 66, 123, 178, 191, 95.6],
[ 77, 75, 75, 22, 52, 66, None, 82.5, 118, 131, 35.7],
[ 82.4, 79.2, 78.1, 79, 95.4, 123, 82.5, None, 76.7, 138, 65.2],
[ 85.5, 82.2, 81.1, 134, 98.5, 178, 118, 76.7, None, 78.7, 83.7],
[ 73.7, 71.4, 70.3, 148, 90.0, 191, 131, 138, 78.7, None, 101],
[ 46.9, 44.6, 43.5, 52.3, 31.9, 95.6, 35.7, 65.2, 83.7, 101, None]
]
次に, 動的計画法のアルゴリズムです。
まず, 最小コストを導出する関数。今回の場合, 最短経路の合計距離になります。
@lru_cache(None)
def tsp_dp(mask, pos):
# 全ての都市を訪問したか確認
if mask == (1 << n) - 1:
return cost_matrix[pos][0] if cost_matrix[pos][0] is not None else INF
min_cost = INF
# 全ての都市を訪問
for city in range(n):
# すでに訪問済みならばスキップ
if mask & (1 << city):
continue
# 訪問していないならばコストを計算
if cost_matrix[pos][city] is not None:
new_cost = cost_matrix[pos][city] + tsp_dp(mask | (1 << city), city)
min_cost = min(min_cost, new_cost)
return min_cost
そして, 最短経路を求める関数。
def find_tsp_path(mask, pos):
path = [0]
while mask != (1 << n) - 1:
next_city = -1
min_cost = INF
# 全ての都市を訪問
for city in range(n):
# 訪問済みならばスキップ
if mask & (1 << city):
continue
# 訪問していないならばコストを計算
if cost_matrix[pos][city] is not None:
new_cost = cost_matrix[pos][city] + tsp_dp(mask | (1 << city), city)
# さらにコストの小さい経路が見つかれば更新
if new_cost < min_cost:
min_cost = new_cost
next_city = city
path.append(next_city)
mask |= (1 << next_city)
pos = next_city
path.append(0)
return path
今回の始点は松山空港(0 番)なので,
initial_mask = 1
initial_pos = 0
を各関数に入れてあげましょう。
min_cost = tsp_dp(initial_mask, initial_pos)
path = find_tsp_path(initial_mask, initial_pos)
print("最短距離:", min_cost)
print("最短ルート:", path)
結果
答えは次のようになりました。
[0,2,1,9,8,7,3,5,6,10,4,0]
松山空港 → 松山城 → 道後温泉 → マイントピア別子 → 石鎚山 → 四国カルスト
→ 宇和島城 → 市場食堂 → 宇和米博物館 → 内子の街並み → 下灘駅 → 松山空港 (または逆ルート)
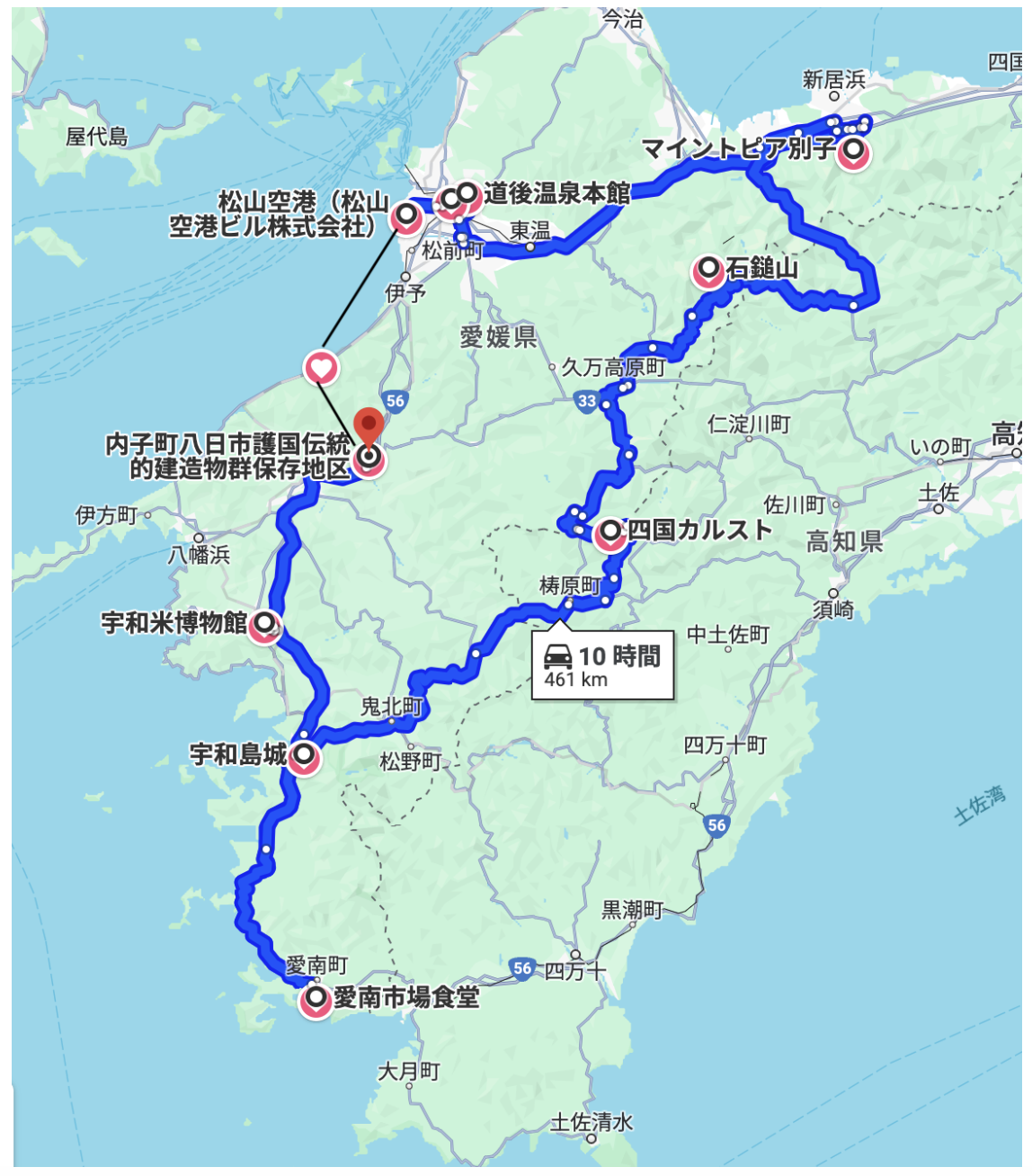
ルートを可視化すると下の図のようになります。Google Map が 10 個までしか中継地点を登録できなかったので, 最後のルートが黒線になっています。
ルートの合計距離は519.5kmとなりました。車での移動が前提ですが, 観光時間も含め 4~5 日あれば周れるのではないでしょうか。ルートをベースに旅行計画を立てたので, より現実味のある旅行プランとなりました。これならきっと, みんな愛媛に来てくれますね!
参考文献
[1] 近畿日本ツーリズム, 愛媛を訪れたら絶対に行くべき観光スポットをご紹介!
https://www.knt.co.jp/travelguide/kokunai/061/
[2] いよ観ネット, 愛媛県の公式観光サイト
https://www.iyokannet.jp/
[3] 楽天トラベル, 愛媛県のおすすめ観光スポット 22 選!
https://travel.rakuten.co.jp/mytrip/ranking/spot-ehime