はじめに
フリースローって難しいですよね。私はやったことありませんが。
きっとフリースローの成否には, 感覚・緊張度合いなどの精神的な要因や, 体調・疲れ度合いなどの身体的な要因など, さまざまなものが関わっているのだと思います。しかし今回はそれらをガン無視して「投射角」に焦点を絞って, フリースローが決まるのに必要な角度を算出したいと思います。全く同じ速度でボールを投げられるロボットをイメージするのが良いと思います。
問題設定
今回の問題設定はこんな感じになります。
「特定の条件下でフリースローを決めるのに必要な角度を求めたい」
では, その特定の条件を今から決めます。
変数は投射角 $θ_0[°]$ のみです。他のパラメータは定数としますが, これらも変数とすることで, さまざまな問題設定に対応することができます。ぜひ, 他の数値を変化させて, 答えを求めてみてくださいね。
ChatGPT にお願いして, パラメータの設定を手伝ってもらいました。以下のように決まりました。おおよそ現実に則っているかと思います。
| パラメータ | 表記 | 値 |
|---|---|---|
| 投射角 | $θ_0$ | $– \ [°]$ |
| 初速 | $\lVert \mathbf{v_0} \rVert$ | $8.0 \ [m/s]$ |
| ボールの質量 | $m$ | $0.5 \ [kg]$ |
| ボールの直径 | $φ_{ball}$ | $24.5 \ [cm]$ |
| リングの内径 | $φ_{ring}$ | $45 \ [cm]$ |
| 空気抵抗係数 | $c$ | $0.015$ |
| 身長 | $h$ | $2 \ [m]$ |
モデリング
では, 肝となる運動方程式のモデリングを設定しましょう。2次元のモデルを考えます。
$$
m \frac{d\mathbf{v}}{dt} = -m \mathbf{g} - c |\mathbf{v}| \mathbf{v}
$$
このモデルはかなりシンプルで, ボールにかかる力は
- 重力
- 空気抵抗
の2つのみです。この他にも
- 回転による揚力
- 浮力
- 跳ね返りの力(リングに当たった時など)
- 外乱(風など)
などが考えられますが, 今回は無視します。
解法
さあ, あとは解くだけです。今回の運動方程式は, 非線形のベクトル微分方程式であり, 解析的な解を導くのが困難です($ \mathbf{g} $ と $ \mathbf{v} $ が同じ方向なら可能)。そのために使うのが 数値計算 です。
数値計算にはさまざまな手法が存在します。せっかくなので, いくつかの手法で比較してみましょう。今回扱う手法は以下の3つです。
- オイラー法
- ホイン法
- ルンゲクッタ法
自分よりも上手に説明してくれる人がいっぱいいるので, 詳しい説明は省きたいと思います。気になった方は, 是非以下のヨビノリさんの動画を参考にしてみてください。
実装
まずは初期条件を設定しましょう。
# 初期条件
θ_0 = math.radians(int(input())) # 投射角
v_0 = 8 # 初期速度
g_0_vec = np.array([0, 9.806]) # 重力ベクトル
v_0_vec = np.array([v_0 * math.cos(θ_0), v_0 * math.sin(θ_0)]) # 速度ベクトル
x_0_vec = np.array([0, 2]) # 位置ベクトル
m = 0.5 # ボールの質量
φ_ball = 0.245 # ボールの直径
φ_ring = 0.45 # リングの内径
c = 0.015 # 空気抵抗係数
次に, 時間変数を設定します。tmin と tmax は, 計算する運動方程式の時間です。dt は 刻み幅 と言い, どれくらいの精度で運動方程式を解くか決める変数です。これが小さいほど正確に軌道を計算できますが, その分計算量が増えるというトレードオフがあります。そのため, ただ小さくすれば良いということではなく, 適切な値を設定する必要があります。今回は $dt=0.001$ とします。
# 時間変数
tmin = 0.0
tmax = 2.5
dt = 0.001
t = tmin
そして, ゴールに入るかどうかの検証には, グラフの描画を使います。
# グラフ用
frames = []
fig = plt.figure()
plt.xlim(0,5)
plt.ylim(0,6)
ax.set_title(f"θ = {θ_deg}°")
ax.set_xlabel("x [m]")
ax.set_ylabel("y [m]")
ax.grid()
ax.set_aspect('equal') # アスペクト比固定
# ゴール(水平線)
ax.plot([x_min, x_max], [y_ring, y_ring], color='orange', linewidth=4, label="Goal Ring")
# ゴールフラグ
goal_in = False
ゴールしたかどうかは, 以下の関数で定義します。ゴールの定義についても, 議論のしがいがありそうですが, ここではボールとゴールのそれぞれの中心間の距離で計算しています。
def is_goal(x, y, prev_y):
ring_center = np.array([4.2, y_ring])
ball_center = np.array([x, y])
distance = np.linalg.norm(ball_center - ring_center)
passes_through = distance <= (φ_ring - φ_ball) / 2
from_above = prev_y > y_ring and y <= y_ring
では, 各手法を実装しましょう。
# オイラー法
def euler(x_0_vec, v_0_vec, t):
x = x_0_vec.copy()
v = v_0_vec.copy()
x_plot = []
y_plot = []
while t < tmax:
prev_y = x[1]
# オイラー法で更新
a = -g_0_vec - (c/m) * np.linalg.norm(v) * v
v = v + a * dt
x = x + v * dt
t += dt
# ホイン法
def heun(x_0_vec, v_0_vec, t):
x = x_0_vec.copy()
v = v_0_vec.copy()
x_plot = []
y_plot = []
while t < tmax:
prev_y = x[1]
# ホイン法で更新
a = -g_0_vec - (c/m) * np.linalg.norm(v) * v
v_pred = v + a * dt
a_pred = -g_0_vec - (c/m) * np.linalg.norm(v_pred) * v_pred
v = v + 0.5 * dt * (a + a_pred)
x = x + 0.5 * dt * (v + v_pred)
t += dt
# ルンゲクッタ法
def rk4(x_0_vec, v_0_vec, t):
x = x_0_vec.copy()
v = v_0_vec.copy()
x_plot = []
y_plot = []
while t < tmax:
prev_y = x[1]
# ルンゲクッタ法で更新
k1 = -g_0_vec - (c/m) * np.linalg.norm(v) * v
v2 = v + 0.5 * dt * k1
k2 = -g_0_vec - (c/m) * np.linalg.norm(v2) * v2
v3 = v + 0.5 * dt * k2
k3 = -g_0_vec - (c/m) * np.linalg.norm(v3) * v3
v4 = v + dt * k3
k4 = -g_0_vec - (c/m) * np.linalg.norm(v4) * v4
a = (k1 + 2*k2 + 2*k3 + k4)/6
v = v + dt * a
x = x + dt * v
t += dt
ゴール判定やグラフ描画の部分を, それぞれの関数に入れてやってください。
# ゴール判定
if not goal_in and is_goal(x[0], x[1], prev_y):
goal_in = True
# プロット準備
x_plot.append(x[0])
y_plot.append(x[1])
traj_line, = ax.plot(x_plot, y_plot, "b")
# ボールの色をゴールインで切り替え
color = "green" if goal_in else "red"
ball = plt.Circle((x[0], x[1]), radius=φ_ball/2, color=color)
ax.add_patch(ball)
frames.append([traj_line, ball])
こんな感じで実行すると, アニメーションを表示することができます!
def main():
euler(x_0_vec, v_0_vec, t)
ani = animation.ArtistAnimation(fig, frames1, interval=10, blit=True)
plt.legend()
plt.show()
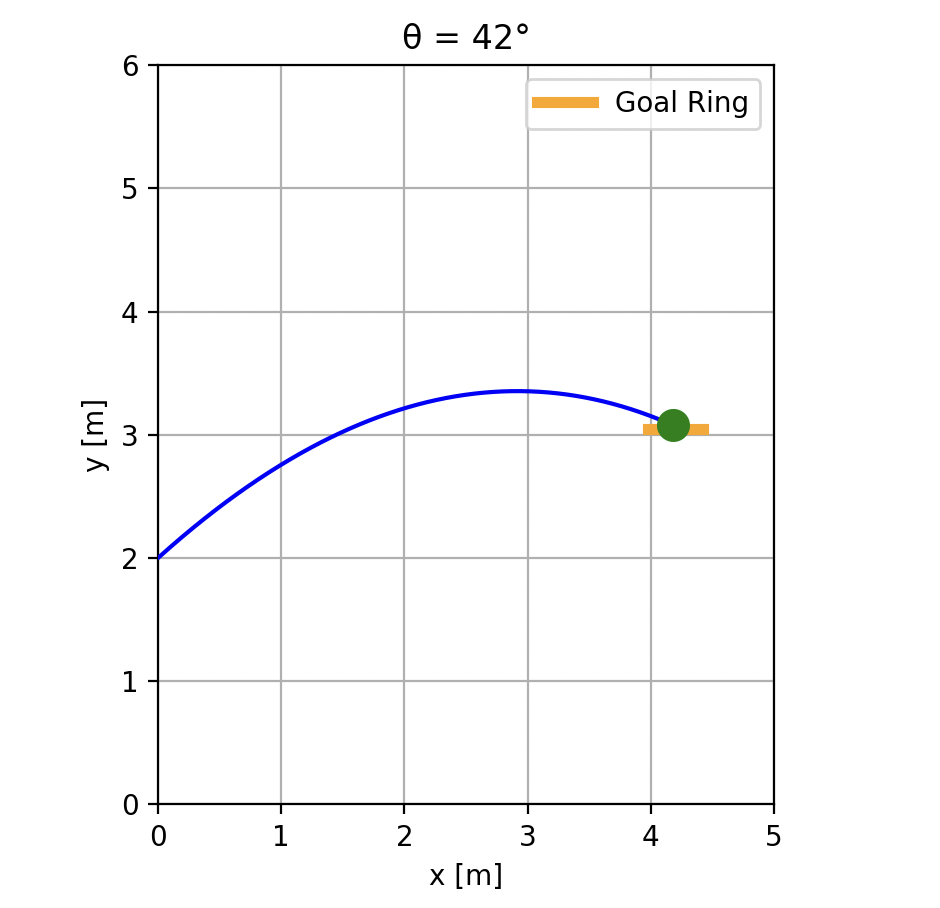
以下は, オイラー法で $θ=42°$ をプロットしたものになります。
角度を変えながら試した結果, フリースローが入るのは 41° ~ 43° という結果になりました。かなりシビアな結果になりましたね...。やはり速度も変数とした方が, いろいろなコースが見えてきそうですが, Future Work とさせていただきます。
V&V (Validation and Verification)
運動方程式のモデルを数値計算で解くことにより, 答えを導くことができました。しかし, 中には違和感を持った方もいるかもしれません。それはこんな感じでしょうか?
- 回転などを考慮しなかったけど, それはよかったの?正しくモデリングしていると言えるの?
- 数値計算の方法によって答えが変わったけど, 本来得られる解は一つじゃないの?
これらの疑問は正しいです。一般的な数値計算, いわゆるシミュレーションの世界では, 誤差などがつきものです。よって, シミュレーションの信頼性を担保することが非常に重要です。
今回の違和感を解消するためのプロセスとして, 前者を Validation(妥当性確認), 後者を Verification(検証) と言います。これらの品質保証のステップを, 頭文字をとって V&V と呼びます。
これらを満たして初めて「正しい予測ができた」と言えるわけです。
数値計算のための Verification 「収束率」
今回の場合, Validation の問いは
「このモデルはフリースローの軌道を正しく再現しているか?」
となります。回転や外乱を考慮しなくても十分正しいかどうかを検証するには, 実際にフリースローをロボットに投げさせて照らし合わせるのが良いでしょう。しかし今回はそんなことできないので, Verification のみ行うこととしましょう。
Verification の問いは
「与えられた運動方程式を数値的に正しく解けているか?」
となりますね。数値計算においては, これを測る尺度が存在します。それが 収束率 です。
収束率とは、数値解が刻み幅(時間ステップ)を小さくしたときに、どれだけ速く真の解(解析解)に近づいていくかを示す指標です。より具体的には、刻み幅 $h$ を小さくしたとき、誤差がどのような割合で減少するかを次のような形で表します。
以下に, オイラー法, ホイン法, ルンゲクッタ法のそれぞれで収束率を求め, 刻み幅を変えてプロットした結果です。それぞれ
- オイラー法は刻み幅が 1/10 になると誤差が 1/10 になる
- ホイン法は刻み幅が 1/10 になると誤差が 1/100 になる
- ルンゲクッタ法は刻み幅が 1/10 になると誤差が 1/10000 になる
ことがグラフからわかります。つまり、ルンゲクッタ法が一番運動方程式を高精度に解けていることがわかります。これは、同じ刻み幅を使ってもルンゲクッタ法が最も小さな誤差を持ち、あるいは同じ誤差を許容する場合に最も大きな刻み幅を使えることを意味します。効率と精度の両面において最も優れた手法であると言えますね。
ただし、高精度な手法はその分、1ステップあたりの計算コストが高くなります。たとえば、ルンゲクッタ法は1ステップで4回の関数評価を行うため、単純なオイラー法よりも計算量は多くなります。実際のシミュレーションでは、精度と計算コストのバランスを考慮して手法を選びましょう。
おわりに
バスケットボールの軌道を運動方程式でモデリングし, 数値計算によって解きました。また, 数値計算の方法が正しく解を得られるのか, 収束率を使って Verification しました。
速度を変数としてみたり, 回転やリング付近のバウンドの動きをモデリングするなど, まだまだできることは多そうです。また, 自分でフリースローを打って Validation してみてもいいかもしれませんね。
参考文献
[1] シミュレーションにおけるV&Vとは?詳細と手順についてご紹介
https://x-simulation.jp/blog/82
[2] 数値計算の基本(微分方程式の扱い)
https://www.youtube.com/watch?v=4lbbgzPeD9I