はじめに
本記事は、「QualiArts Advent Calender 2024」の21日目の記事になります。
最近、「Banach-Tarskiの定理(バナッハ=タルスキーの定理)」の話題を目にしない日はないほど、巷で盛り上がっています。
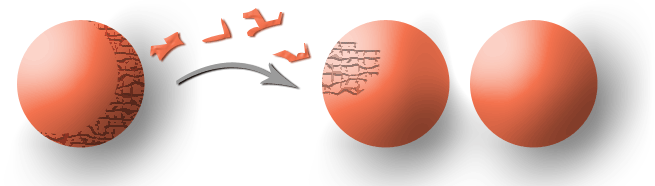
「Banach-Tarskiの定理」とは、1つの球を分解して組み立てると全く同じ球が2つになるという、とても不思議な定理です。
どう考えてもおかしいですよね。例えば、サッカーボールをバラバラにして組み合わせると同じ大きさのサッカーボールが2つになると言うことです。
普通に考えるとおかしなことを言っている定理ですが、数学的にきちんと証明がされています。
本記事ではそんな奇妙な現象を起こす「Banach-Tarskiの定理」について見ていきます。
厳密性よりも雰囲気で分かってもらえるようにわかりやすさを優先しています。
Banach-Tarskiの定理
Banach-Tarskiの主張は次のとおりです。
球を3次元空間内で、有限個の部分に分割し、それらを回転・平行移動操作のみを使ってうまく組み替えることで、元の球と同じ半径の球を2つ作ることができる (wikipediaより)
有限個の部分への分割に関しては5個で行えることも分かっています。
「Banach-Tarskiの定理」は数学的に証明がされている立派な定理ですが、その内容が人間の直感に反することから「Banach-Tarskiのパラドックス」とも呼ばれています。
直感的ではない理由
証明の内容の前に先になぜ直感的ではないのかについて考えます。
私は直感的でない理由の一つに、「Banach-Tarskiの定理」の内容をそのままの日本語で解釈しようとしているからだと考えます。
例えば、以下の整数と有理数の集合に関する式があるとします。
$$|\mathbb{Z}| = |\mathbb{Q}|$$これは整数の集合 $\mathbb{Z}$ と 有理数の集合$\mathbb{Q}$ の個数(濃度)が同じであることを示しています。
これを見て、「個数が同じと言っているのに、整数でない有理数が存在するからこの式は直感に反している」とはならないと思います。
なぜなら、ここでいっている「個数が同じ」が「全単射が存在する」という意味で使われていることが分かっているからです。
同じように、実数の集合 $\mathbb{R}$ と 実数の集合 $\mathbb{R}$ の任意の区間が同じといわれても全単射が存在するとわかると思います。
「Banach-Tarskiの定理」の場合は、「有限個に分割する」という部分が問題で、これをそのまま私たちの知っている普通の分割と解釈しようとするため直感に反するのだと思います。「Banach-Tarskiの定理」では球体をかなりやばい方法で分割を行っているため、球が増えるくらい打っ飛んだことが起きてしまうのです。
「Banach-Tarskiの定理」に限らず多くの場合において、数学の公理や定理をそのままの日本語で解釈すると直感に反することが多くあります。直感に反する主張となるトリックがどこかにあるため、なにを行っているのか中身を理解することがとても大切です
なぜBanach-Tarskiの定理は成り立つのか
簡単にではありますが、証明とその流れについてみていきたいと思います。
いくつか証明の前に必要な事前知識がありますので、それも交えてみていきます。
選択公理
選択公理は、無限の集合があった時に、各集合が空ではない場合一つずつ元を選び出すことが可能であるという公理です。公理なので証明することができません。ZFに一般連続体仮説を加えると証明できるらしい
厳密に書くと以下のようになります。
任意の集合族 $\{A_\lambda \mid \lambda \in \Lambda\}$ に対して、任意の $\lambda \in \Lambda$ について $A_\lambda \neq \emptyset$ とすると、
$$
\prod_{\lambda \in \Lambda} A_\lambda \neq \emptyset
$$
つまり、「無限に多くの箱があり、各箱には少なくとも一つのボールが入っている場合、各箱から一つずつボールを取り出して全ての箱を一つのセットにまとめることができる」ということを意味しています。
userの各データ群から欲しいデータを取り出して新しい集合を作る操作を無限のデータ群に対して行えるようにする公理です。
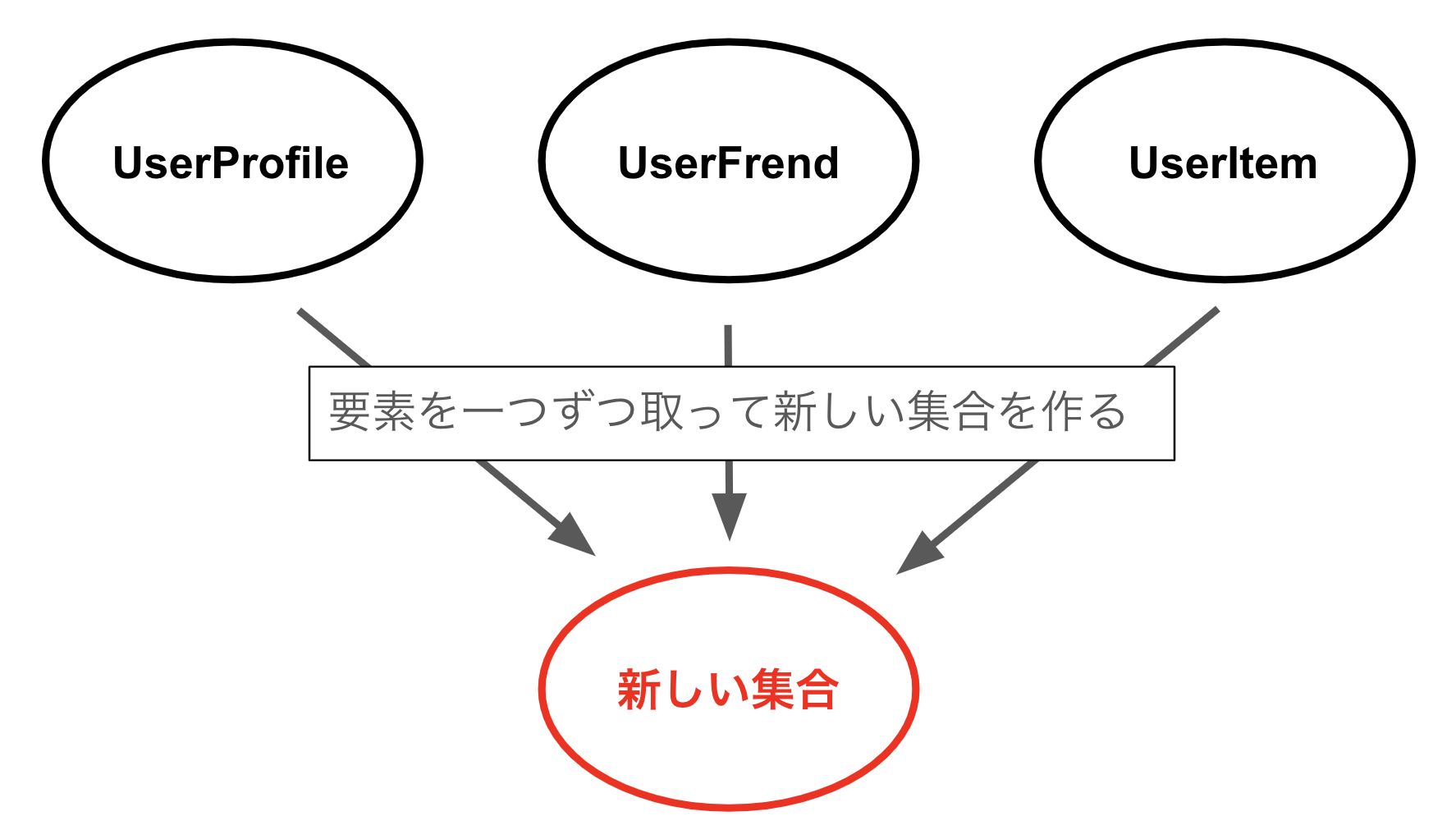
どのようにして無限個の集合から元を取ってくるかや、無限の集合なのでこの操作は一生終わらないんじゃないかなど、不可解なことが多く証明もできないため、こんなことはできないと考える人もいますが、この公理はとにかく無限の集合から元を持ってくることができるようになります。
「Banach-Tarskiの定理」は選択公理を認めると証明できてしまうため、こんなおかしな定理が証明されてしまうなんて選択公理はおかしいと言う人がいたりいなかったりします
回転群
3次元空間における回転群について軽く説明します。
3次元空間における回転群 ( SO(3) ) は、原点を中心にして空間を回転させる操作全体の集合です。回転群は空間内の点の位置関係を保ちながら回転を行います。具体的には、以下の操作を含みます:
- 回転:部分集合を詳細な回転軸を中心に回転させる
回転群の作用を通じて、3次元空間内では物体の形状や大きさを変えずに位置や向きを変えることができます。この概念がBanach-Tarskiの定理の基盤となります。
集合の測度
一般の集合における面積や体積っぽいものを定義する必要もあります。
なぜ面積や体積っぽいといった曖昧な表現を使っているかは後ほど出てきます。
$X$: 集合、$G$: 群で $G$ が $X$ に作用しているとします。このとき、集合関数 $m: X \to \mathbb{R}$ で以下の条件を満たすものが存在します。
任意の $\forall A \subset X$ について、
- $m(A) \geq 0$ (測度は常に非負である)
- 任意の $g \in G$ に対して $m(gA) = m(A)$ (群の作用によって測度は変わらない)
- $A = A_1 \cup \cdots \cup A_n$ のとき、$m(A) = m(A_1) + \cdots + m(A_n)$ (集合の分割に対して測度の加法性が成り立つ)
この$m$が集合の面積っぽいものを算出します。
一般化しているため、特定の次元に依存しません。
そのため、面積や体積、長さなのか分かりませんが、そういった類のものを算出します
(これが曖昧な表現理由です。)
$m$のことは数学ではよく測度と言い、集合がどれだけの「量」を持つかを定量化しています。
群の測度
先ほど、一般の集合の測度を定義しました。
群$G$も集合なので、群にも測度が定義できそうですよね。
測度$m$をもつ群を amenable群(従順な群) といいます。
すべての群に測度が定義できるわけではありません。
ここで自由群$F_2$を考えます。詳細は省きますが、自由群$F_2$はamenable群ではありません。
そのため自由群 $F_2$ には一貫した測度を割り当てることができないのです。
自由群 $F_2$の大きさは定義できなんだなーぐらいの認識で大丈夫です。
この一貫した測度を持たない群の性質が「Banach-Tarskiの定理」の奇妙な現象のおいてとても重要な存在になります。
逆説的集合
次に、逆説的集合の定義と性質について説明します。
ここから若干難しくなっていきます。
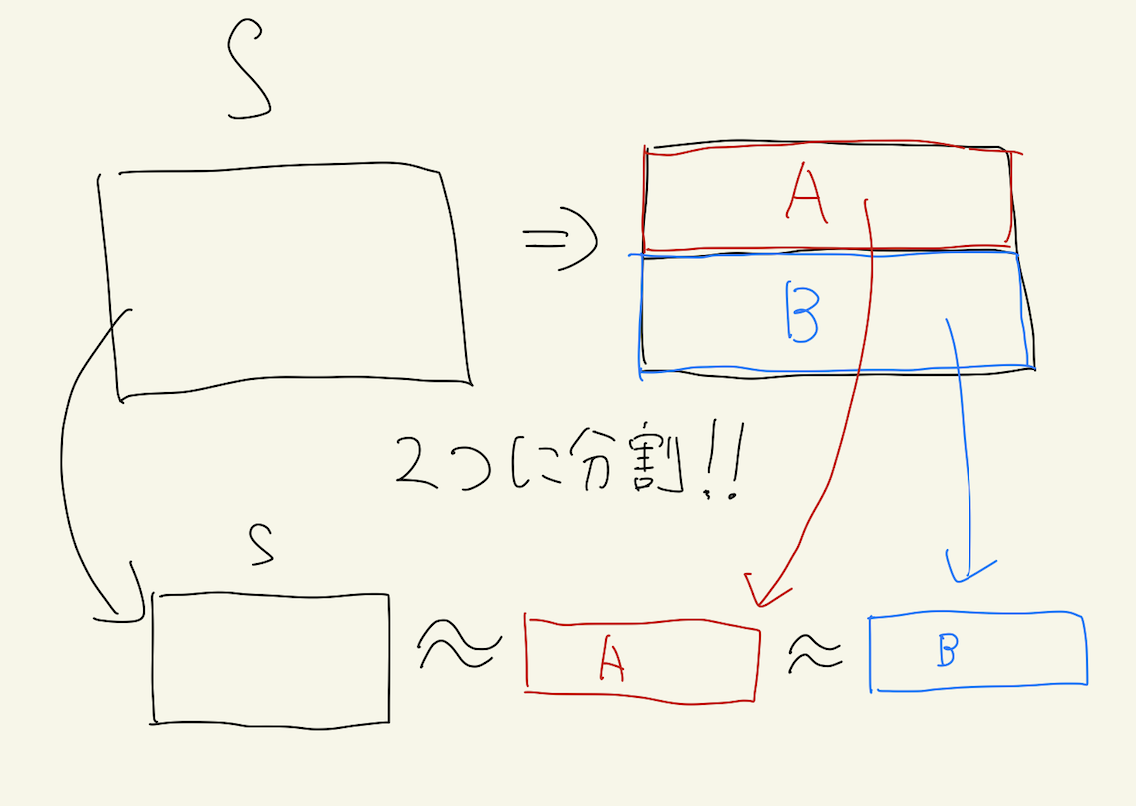
逆説的集合とは、全体を2つの部分集合に完全に分割でき、それぞれの部分集合が分割前の全体と「分割合同」であるような集合のことを指します。具体的には、集合 $S$ が逆説的であるとは、$S$ を $A$ と $B$ という2つの部分集合に分割し、$A \cap B = \emptyset$ かつ $A \cup B = S$ であり、かつ $A$ と $B$ がそれぞれ $S$ と分割合同であることを意味します。つまり、以下の条件を満たします:
- $A \cap B = \emptyset$ (AとBは重ならない)
- $A \cup B = S$ (AとBを合わせると全体Sになる)
- $A \approx S$ および $B \approx S$ (AとBがそれぞれSと分割合同である)
ここで「分割合同」とは、有限個の部分に分割し、それらの部分が互いに合同変換(回転、平行移動、反射など)によって一致することを意味します。
面積が同じで違う図形があったときに、片方の図形を細かく切ってうまく繋ぎ直せばもう片方の図形と同じ形にできますよね。この状態を2つの図形は分割合同といいます。
この性質を持つ集合が存在すること自体が直感に反するかもしれませんが、実際にはこのような集合は存在します。
その最たる例が自由群$F_2$です。
2つの生成元$a$,$b$をもつ自由群$F_2$について、以下の分割を行います。
- $a$から始まる集合:$S(a)$
- $b$から始まる集合:$S(b)$
- $a^{-1}$から始まる集合:$S(a^{-1})$
- $b^{-1}$から始まる集合:$S(b^{-1})$
- 単位元の集合$e$ (単位元が唯一の元の集合)
このとき、
\begin{align}
F_2 &= S(a) + S(b) + S(a^{-1}) + S(b^{-1}) + {e} \\
&= a^{-1}S(a) + S(a^{-1})
\end{align}
となります。
集合の測度の2つ目によると、群の作用によって測度は変わらないはずなので、$S(a)$と$a^{-1}S(a)$の測度は変わらないはずです。
しかし、自由群 $F_2$ の測度は一貫しません。
$$m(S(a)) = m(a^{-1}S(a))$$であるべきですが、測度は定義されないために測度守る法則が破られる場合が起こってしまいます。
このようにして、矛盾が生じることにより、$S(a)$または$a^{-1}S(a)$の測度は定義不可能になります。したがって、逆説的集合が形成され、点集合の集まりが逆説的な性質を持つことになります。
この自由群$F_2$の性質が「Banach-Tarskiの定理」の証明においてとても大切です。
自由群$F_2$ の作用を考慮することで、空間内に逆説的集合を構築することができます。
Banach-Tarskiの定理はこの逆説的集合の性質を利用して、球体の奇妙な分割と再構築を行っています。
逆説的集合の伝播
先ほどの逆説的集合の性質は空間に伝播する場合があります。
群 $G$ が逆説的集合であり、集合 $X$ に自由に作用するとき、集合 $X$ も逆説的集合になります。
自由群 $F_2$ が逆説的集合であるため、それが作用する空間も逆説的集合になってしまうということです。
そしてこの証明に選択公理を使います。
自由群 $F_2$ が集合 $X$ に自由に作用する場合、$X$ の各要素に対して $F_2$ の任意の元を適用して移動させます。このときに、以下の操作が必要になります:
- 集合 $X$ をいくつかの部分集合に分割します。このとき $X$ の各要素がどの部分集合に含まれるかを決定する必要があり、各要素に対応する無限の選択を行います
- 各部分集合の要素を自由群 $F_2$ の各元に対応して要素を移動させます。このときも同じように無限の選択を行います
これらの操作を行うのに選択公理が必要になります。
3次元空間での回転群
いよいよ最後の「Banach-Tarskiの定理」がなぜ成り立つのかの部分です。
3次元空間に作用する回転群$SO(3)$の部分集合の中に自由群$F_2$と同じ構造(同型)を持ったものが存在します。
これによって、3次元空間内に部分集合の中に逆説的集合となるものが存在することになります。
逆説的集合は先ほど述べたとおり伝播するので、3次元空間で「Banach-Tarskiの定理」が成り立つことになります。
かなり細かなお話や厳密性を置き去りにしていますが大まかな証明のながれでした。
これで無事「Banach-Tarskiの定理」が成り立つ理由まで辿り着けたと思います。
まとめ
「Banach-Tarskiの定理」が直感的ではない理由と証明の流れを見てきました。
自由群$F_2$が測度を持たないことと選択公理によって逆説的集合が空間に伝播するのがこの定理の真相でした。
これは余談なのですが、なぜ2次元では「Banach-Tarskiの定理」が成り立たないのかを軽く説明します。
回転群から自由群$F_2$を生み出すには回転群が非可換である必要が実はあります。
2次元の回転群は可換なんで自由群は作られず、回転群が非可換である3次元でのみ成り立つことになります。
世の中にはLean4で「Banach-Tarskiの定理」を定式化するプログラムも存在するそうです。
この記事を読んでもし「Banach-Tarskiの定理」に興味を持った方はぜひ詳しく勉強して参加しましょう!
最後に
以上、21日目の記事でした。残りの日数も少なくなってきましたね。
引き続き今後のカレンダーも宜しくお願いします。
参考文献