最近スマホのゲームで数独を解くのにハマっている。
紙とペンで解く時は、数値の入る可能性のあるマスを探し出し、そこに数値を当てはめていくが、
スマホなどのデバイスで解く場合は、一旦全部のマスに全部の数値を代入してしまったのち、決定済みのマスから、同じ数値の入る可能性のないマスを探し、その数値を消していく、"引き算"で考えたほうが早い。
自分はいつもその手法で解いているのだが、その手法がアルゴリズム(?)的にどんな問題でも毎回ちゃんと解けるものなのかプログラム書いて試してみた。
結論から言うと解けない問題もあったので、必ず解けるプログラムが組みたい人は、片っ端から順番に代入していく総当たりの方法を検討することをお勧めする。(後述)
解き方(イメージ)
まずこういった問題があったとして
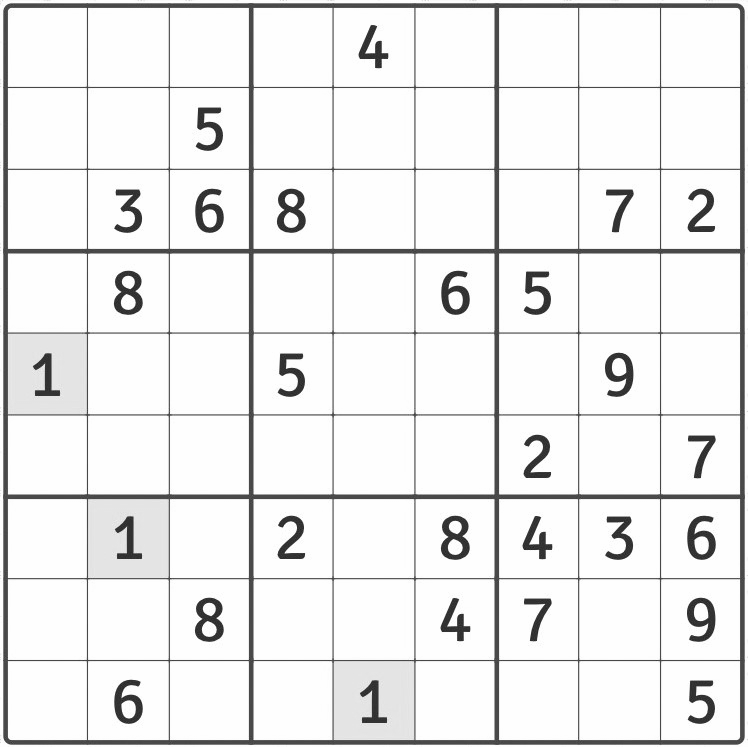
①数値の決定していないすべてのマスに対して一旦すべての数字を代入する

②決定している要素ひとつずつに注目し、その数値を縦、横、その数字が存在する3x3マス内から消していく
(この図は左真ん中の"1"に関して操作した後。これを決定済みの全数値に対して繰り返す。)

③今度は縦、横、3x3内に注目し、その要素内で一つしか入りえない値を、決定値として入れていく
(この図の場合、左上の3x3内には"1"が一ヶ所しか入らないため、ここに"1"が決定する。)
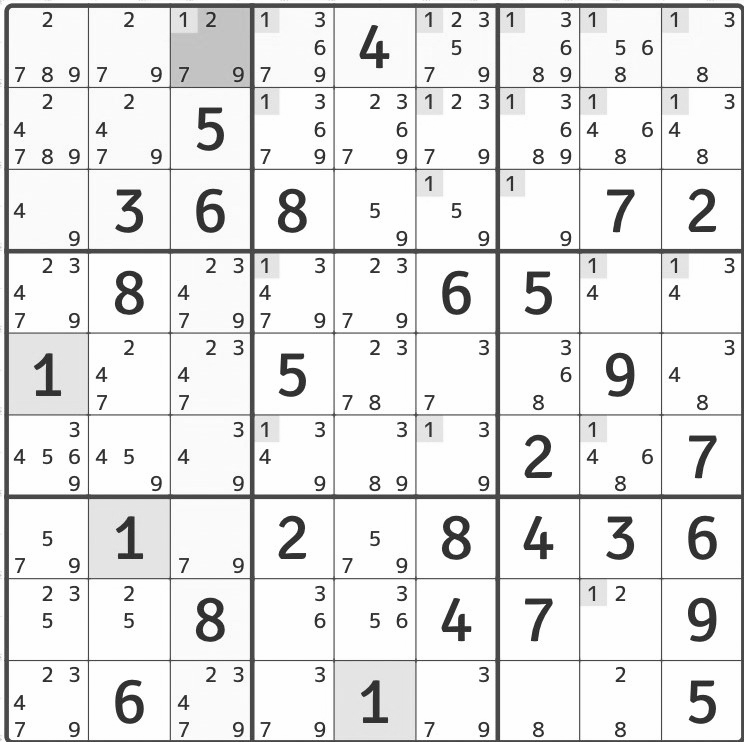
④これらの操作の繰り返し。
これをプログラムで実装する。
コード
import numpy as np
import copy
xx = [1, 2, 3, 4, 5, 6, 7, 8, 9]
x1 = [1]
x2 = [2]
x3 = [3]
x4 = [4]
x5 = [5]
x6 = [6]
x7 = [7]
x8 = [8]
x9 = [9]
lists = [
[copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x4), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx)],
[copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x5), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx)],
[copy.deepcopy(xx), copy.deepcopy(x3), copy.deepcopy(x6), copy.deepcopy(x8), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x7), copy.deepcopy(x2)],
[copy.deepcopy(xx), copy.deepcopy(x8), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x6), copy.deepcopy(x5), copy.deepcopy(xx), copy.deepcopy(xx)],
[copy.deepcopy(x1), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x5), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x9), copy.deepcopy(xx)],
[copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x2), copy.deepcopy(xx), copy.deepcopy(x7)],
[copy.deepcopy(xx), copy.deepcopy(x1), copy.deepcopy(xx), copy.deepcopy(x2), copy.deepcopy(xx), copy.deepcopy(x8), copy.deepcopy(x4), copy.deepcopy(x3), copy.deepcopy(x6)],
[copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x8), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x4), copy.deepcopy(x7), copy.deepcopy(xx), copy.deepcopy(x9)],
[copy.deepcopy(xx), copy.deepcopy(x6), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x1), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(xx), copy.deepcopy(x5)],
]
cells = np.array(lists)
flags = np.zeros((9, 9))
grid = [(0, 3), (3, 6), (6, 9)]
while np.any(flags==0):
for i, ii in enumerate(cells):
for j, jj in enumerate(ii):
if len(jj) == 1 and flags[i, j] == False:
num = jj[0]
flags[i, j] = True
# 縦、横、方向に検索し、同じ数字は削除
for kk in cells[i]:
if num in kk and len(kk) != 1:
kk.remove(num)
for kk in cells[:, j]:
if num in kk and len(kk) != 1:
kk.remove(num)
# 3x3内で、同じ数字は削除
if i < 3:
l = 0
elif i >= 3 and i < 6:
l = 3
elif i >= 6 and i < 9:
l = 6
if j < 3:
d = 0
elif j >= 3 and j < 6:
d = 3
elif j >= 6 and j < 9:
d = 6
for ll in cells[l:l+3, d:d+3]:
for mm in ll:
if num in mm and len(mm) != 1:
mm.remove(num)
for ii in range(1, 10):
# 縦、横、方向に検索し、数字が一つしか入らない場合は決定
for jj in range(0, 9):
counter1 = 0
counter2 = 0
marker1 = 0
marker2 = 0
for kk in range(0, 9):
if ii in cells[jj, kk]:
counter1 += 1
marker1 = kk
if ii in cells[kk, jj]:
counter2 += 1
marker2 = kk
if counter1 == 1:
cells[jj, marker1].clear()
cells[jj, marker1].append(ii)
if counter2 == 1:
cells[marker2, jj].clear()
cells[marker2, jj].append(ii)
# 3x3内で検索し、数字が一つしか入らない場合は決定
for jj in grid:
for kk in grid:
counter3 = 0
marker3 = 0
marker4 = 0
for mm, ll in enumerate(cells[jj[0]:jj[1], kk[0]:kk[1]]):
for oo, nn in enumerate(ll):
if ii in nn:
counter3 += 1
marker3 = mm
marker4 = oo
if counter3 == 1:
cells[jj[0]+marker3, kk[0]+marker4].clear()
cells[jj[0]+marker3, kk[0]+marker4].append(ii)
# print用配列の作成
num_list = []
for ii in cells:
_num_list = []
for jj in ii:
if len(jj) == 1:
_num_list.append(jj[0])
else:
_num_list.append(0)
num_list.append(_num_list)
print("---------------------------")
for ii in num_list:
print(ii)
print("---------------------------")
numpyを使う練習をしたかったのも目的の一つだったので、一応使用している。
1~9の入ったリストを9x9で持っている三次元配列に対して、そのマスの数値が決定済みかどうか(3次元目の配列の長さが1かどうか)かつ、②の操作を実行済みかどうかをTrue-Falseで管理する9x9の二次元配列で管理しながら、問題を解いている。
実行結果
実行した結果がこちら。
---------------------------
[2, 7, 1, 6, 4, 3, 9, 5, 8]
[8, 9, 5, 1, 7, 2, 3, 6, 4]
[4, 3, 6, 8, 9, 5, 1, 7, 2]
[7, 8, 3, 9, 2, 6, 5, 4, 1]
[1, 4, 2, 5, 8, 7, 6, 9, 3]
[6, 5, 9, 4, 3, 1, 2, 8, 7]
[9, 1, 7, 2, 5, 8, 4, 3, 6]
[5, 2, 8, 3, 6, 4, 7, 1, 9]
[3, 6, 4, 7, 1, 9, 8, 2, 5]
---------------------------
最後に
こちらのロジックだけではどうやら解けない問題が存在するようで、そういった問題を解こうとするとwhileが回り続けてしまう。
今回調べてみてわかったが、どうやら数独にも様々な解き方が存在するようで、この解き方では何かが足りない模様(何かは分からないが。。)
今回は数独のすべての問題を解くことが目的ではなかったので、ひとまず確認のみで終わっておいた。
もし、続きを仕上げたい方がいれば下記が参考になると思う。
一応、総当たりよりは高速に仕上がるかなと思う。
どんな問題でも、とにかく解きたい!って方は、冒頭でも述べたように、以下のような総当たりの方法をとることをお勧めする。
また、今回は普通に解いただけだったが、それだけだと面白くないので、画像や写真から問題を認識して解くようにした。
次回その辺について書く。